模糊控制系统模型在轴承故障诊断中的应用

欧阳承达，张 军，赵红梅

（1.广东工业大学华立学院，广东 广州 511325；2.广州华立科技职业学院，广东 广州 511325）

机械故障诊断具有复杂性、随机性以及征兆的局限性，为了对其进行故障定位，人们在进行故障诊断时往往是通过“清晰”的机械故障信息量来获得故障认知、故障分析以及故障决策。但现实中，得到“清晰”所含有的机械故障信息量需要依赖精准的数学模型来进行诊断，精准的数学模型往往会导致系统过于复杂[1-2]。一般说来，自动化程度越高、系统越复杂的机械设备，其故障的模糊性也就越强，传统的诊断方法是无法给出故障与征兆之间的定量分析的［3］。模糊诊断模型正好能完成对于不确切和随机性的描述，且模糊集理论对根据机械故障建立的数学模型要求不高。因此，在模糊集理论基础上，根据机械故障选择对应的隶属函数和模糊规则，建立故障诊断系统模型就显得十分重要［4］。

1 用于故障诊断的模糊控制系统模型

故障诊断的模糊控制系统是一种基于模糊集理论，在机械系统运行过程中，将系统的故障和随机性进行分辨，当出现故障时，及时以故障信号输出的一种监控方式。其主要由模糊向量、诊断矩阵、模糊推理和模糊诊断4个功能模块组成。

1.1 模糊向量

（1）特征模糊向量。假设某类机械故障发生时产生了n个特征，其论域为U={x1，x2，…，xn}，其中，描述第i种特征的状态变量为xi（1，2，…，n），对应隶属函数为 μxj，X=（μx1，μx2，…，μxn）称 X 为特征模糊向量。（2）故障模糊向量。假设某类机械故障发生时，可能由m种原因，其论域为W={y1，y2，…，ym}，描述第j种原因的状态变量为yj（j=1，2，…，m），对应隶属函数为μyi，Y=（μy1，μy2，…，μyn）称Y为故障模糊向量。

1.2 诊断矩阵

机械系统的设备零部件之间总是存在着相关性，常用符号R来表示对事物之间联系的数学模型。因此，在机械诊断中，征兆与故障必然会存在着相应的关系，通过特征模糊向量U到故障模糊向量W来构建诊断关系矩阵R，用序对（x，y）来表示。其中，x属于特征模糊向量U，y属于故障模糊向量W。在集U和集W的直积集，记为U×W={（x，y） x∈X，∈Y}，诊断矩阵R是定义在直积U×W上的模糊集合，表示如下：

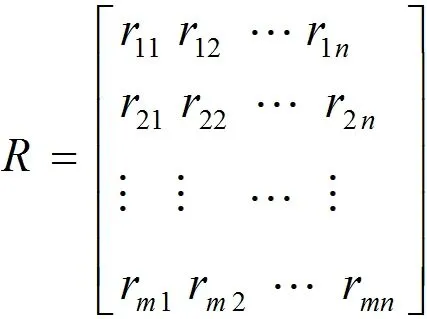
该集合表示故障原因与特征之间的因果关系。

1.3 模糊推理

设R为U到W的一个模糊关系，则由模糊关系R（x，y）=U→W=U×W；U’得到W上的模糊集W’，在新的特征模糊向量下推导出该特征模糊向量所对应的故障模糊向量，如下：

式中：。为模糊关系合成算子。

1.4 模糊诊断

在模糊控制系统模型中，模糊诊断的实现过程就是根据模糊关系矩阵R及特征模糊向量U’，求得故障模糊向量W’，模糊诊断的结果是要得到实际的控制量。经常采用下面几种方法，将其转换成精确的实际执行量，从而实现模糊诊断结果的输出。

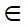
2 模糊控制系统模型在轴承故障诊断中的应用

轴承的工作环境复杂以及其运动特点，使得轴承出现故障也存在着随机性和模糊性特点［5］。模糊集理论适合用来处理类似轴承这样复杂的非线性系统。采集轴承故障诊断数据的试验台安装示意图如图1所示。试验台上安装了1个转轴，转轴两端分别安装了1个轴承座，每个轴承座里面分别安装了1个滚动轴承，转轴上还安装了飞轮来模拟试验系统的负载，用变频器来控制转轴的转速。为了采集轴承运行过程中的振动信号，在每一个轴承座上安装了一个加速度传感器，加速度传感器的输出通过数据采集卡连接到计算机中进行保存，部件及其规格如表1所示。

图1 实验装置示意图

表1 实验装置中使用的具体部件及其规格

试验中，在轴承外圈、内圈和滚动体上分别刻蚀0.18mm和0.36mm的槽，每次测试中的转速、负载和轴承状态类型是不同的，并测试电机转速在1800r/min下的轴承振动数据。由于轴承中故障信号常常是在1～20KHz的频带，因此实验选择采样频率为12KHz。

（1）故障轴承的特征模糊向量的确定。在轴承的故障诊断系统模型构建过程中，故障特征向量要能充分地反映故障的原因，从而推导故障的种类。对采集的原始信号进行故障特征提取，该次试验中的轴承故障诊断数据选取频域的外圈故障特征频率f0处的包络幅值谱的幅值X1、X2，内圈故障特征频率fi处包络幅值谱的幅值X3、X4，滚动体故障特征频率fb处的包络幅值谱的幅值X5、X6。轴承外圈、内圈以及滚动体的振动幅值6个量成故障轴承的特征模糊向量A，所对应的隶属度分别为μX1、μX2、μX3、μX4、μX5、μX6组，记为 A=［μX1μX2μX3μX4μX5μX6］T。

（2）故障轴承的故障模糊向量的确定。故障轴承在外圈、内圈以及滚动体的破损分别表示为外圈轻微破损Y1和严重破损Y2、内圈轻微破损Y3和严重破损Y4、滚动体轻微破损Y5和严重破损Y6等6种故障。轴承外圈、内圈以及滚动体的振动幅值6个量组成为故障模糊向量B，6 种故障所对应的隶属度 μY1、μY2、μY3、μY4、μY5、μY6，记为 B=［μY1μY2μY3μY4μY5μY6］T。

（3）故障轴承的诊断矩阵的确定。设a、b分别为表示故障轴承的“振幅”和“故障”，其论域分别为A和B，并有

在轴承内圈、滚动体、外圈上分别腐蚀直径为0.18mm的槽情况下，通过对采集到的数据进行谱分析，于是得到集合A，设A表示振幅大的特征模糊集合，则：

得到集合B，设B表示故障的模糊集合，则：

模糊蕴含关系矩阵R：

在轴承内圈、滚动体、外圈上分别腐蚀直径为0.36mm的槽，得到特征模糊集合A’，此时设A’振幅非常大的模糊结果：

此时，得到故障模糊集B’的特征向量。

（4）故障诊断分析。根据选择隶属度大的原则，通过对轴承外圈、内圈和滚动体上分别腐蚀直径为0.18mm和0.36mm的槽实验中分析得知，故障模糊集中显示轻微破损的隶属度最高的为b1=0.53，意味着当轴承外圈、内圈或滚动体上在腐蚀直径为0.18mm和0.36mm的槽实验中，轴承外圈最容易受到轻微破损；其次，轻微破损也较大发生在轴承内圈，隶属度为0.45；最后，还可以发现轴承外圈所对应的轻微破损和严重破损隶属度之和是最大轴承外圈，即b1+b2=0.85，轴承损伤最为严重的部位为轴承外圈。

3 结束语

作为旋转机构中最为常见故障之一的轴承故障，如何能够初步获得故障征兆显得十分重要。在模糊糊控制系统模型在轴承故障诊断试验中，通过对振动信号进行谱分析后的包络特征频率，利用隶属度函数得到初始特征模糊向量和初始故障模糊向量，通过初始特征模糊向量和初始故障模糊向量构造模糊关系矩阵，根据模糊关系矩阵对新的特征模糊向量进行故障识别，然后按最大隶属度准则判断出轴承各部件的故障。由此可见，在轴承故障识别中，利用模糊诊断方法，判断轴承是否存在故障，这方法可以将轴承故障进行分级，帮助用户有效识别轴承故障。