斜拉钢混组合结构梁端轨道结构适应性研究

荣亚清，孟乐平，谢德胜，薛垂义，艾 敏，李成彬

（1.中国铁路通信信号股份有限公司，北京 100070；2.中国铁路通信信号上海工程局集团有限公司，上海 200436）

大跨度梁桥的梁端因常受温度荷载、列车活载、墩台沉降或变形等影响，易产生纵向伸缩，垂向错台、折角，甚至横向错动等复杂的空间变形形态[1]。当采用有砟轨道结构时，散体道床具有一定的自调整能力，可适应微量变形的协调问题[2]。当采用无砟轨道结构时，因道床被刚化，缺乏有砟道床的自组织、自调整能力，使得轨道几何形位、扣件系统工作状态和附近的无砟轨道受力均受到不利影响，最终影响到行车安全[3]。

跨东平水道桥主桥上为斜拉钢混组合结构，且城轨、公路与人群荷载同层布设，为大坡道、人字坡布局，是目前国内外罕见的公铁两用柔性体系桥梁。桥上铺设无砟轨道，运营100%低地板的有轨电车，设计时速70km/h。因桥跨结构的特殊性，使得该桥梁端变形复杂，且量值较大，为确保结构安全和行车品质，必须针对该斜拉钢混组合结构的梁端轨道结构适应性进行分析。东平水道桥主桥桥面布置示意图如图1所示，东平水道桥轨道结构断面图如图2所示。

1 计算模型及参数

1.1 计算模型

根据该桥结构特点，采用简化的单线钢轨－无砟轨道－梁体一体化分析模型，各连接界面处理为弹簧连接，如图3所示[4]。作假设如下：

（1）在端部一定长度范围内，认为梁体以刚性变形为主，为方便建模，假定梁体为刚体，仅发生刚体位移，考虑到扣件在纵向上有一定的抗滑移能力，当梁轨相对位移小于2mm时，可认为对扣件间距无影响；当大于2mm时应考虑梁轨相对位移对扣件间距的影响。

（2）扣件、减振垫简化为弹性支承元件。

（3）桥梁对轨道的支承符合Winker假定。

（4）模型根据梁端无砟轨道是否采用伸缩装置，分优化前和优化后两种计算模型。优化前梁端处无砟轨道直接断开，优化后梁端处采用简化的过渡板、抬梁结构模拟梁端伸缩装置。

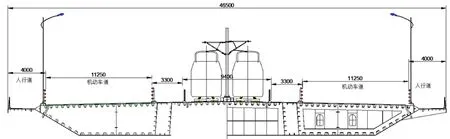
图1 东平水道桥主桥桥面布置示意图（单位：mm）

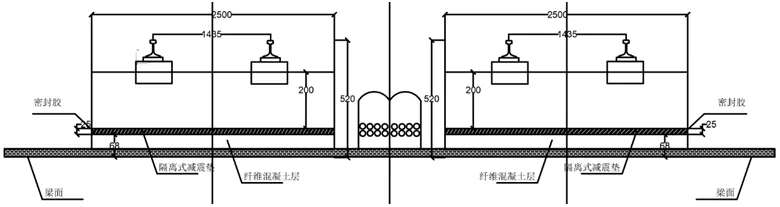
图2 东平水道桥轨道结构断面图（单位：mm）

1.2 主要结构参数

图3 钢轨-无砟轨道-基础（梁体）一体化模型

钢轨为50kg/m标准轨，弹性模量取2.06×1011Pa，泊松比为0.3，线膨胀系数为11.8×10-6℃，密度7800kg/m3。采用G型扣件，常阻力处刚度取50kN/mm，小阻力处刚度取40kN/mm。轨道板混凝土标号C50，板宽2500mm，板长与梁端结构匹配，从2.4～6.0m不等。轨道板弹性模量为3.55×1010Pa，泊松比为0.1667，线膨胀系数为1×10-5℃，厚度为0.2m，密度为2500kg/m3。减振垫弹性模量为0.4×106Pa，泊松比为0.47，厚度为0.025m。底座板（梁板）设置在桥梁上，弹性模量为3.55×1010Pa，泊松比为0.3，不考虑底座板的挠曲变形影响。

1.3 荷载工况

（1）列车荷载。该线路车辆为有轨电车车辆，车辆轴重12.5t，最大速度70km/h。车荷载在直线轨道上作用时，由于动力效应的影响使得作用在钢轨上的动轮载要比静轮载大，而且其增量随着行车速度的增加而增大，因此根据式（1）将列车静轮载转换为动轮载[5]。

式中：Pd为动轮载；P0为静轮载；α为速度系数。根据我国在行车速度V≤200km/h的线路上采用的设计方法，取α=0.42；并在计算钢轨下沉以及轨下基础各部件荷载及应力时，在计算结果基础上乘以0.75的折减系数，得到式（2）[5]：

（2）梁端变形。跨东平水道桥主桥小里程侧与大里程侧的梁端结构均会在温度的影响下产生较大的受力和位移。主桥小里程侧：在最低温作用下，梁面错台水平距离为396mm，垂向高差为7.84mm；在最高温作用下，梁面错台水平距离为18mm，垂向高差为7.28mm。主桥大里程侧：在最低温作用下，梁面错台水平距离为252mm，垂向高差为2.08mm；在最高温作用下，梁面错台水平距离为151mm，垂向高差为1.96mm。由此可知，主桥大里程侧的位移与错台值比小里程侧要小很多，设计时应重点关注小里程侧梁端结构的受力与位移。基于此，文章针对温度变化下跨东平水道桥主桥小里程侧梁端优化前后的受力情况展开仿真计算研究。

2 主要控制标准

根据我国高速铁路桥上无砟轨道的应用经验，在未采取工程措施条件下，梁端变形应控制在垂、横向相对位移1mm，转角控制在1‰以内[5-6]。对于特大型桥梁或特殊桥式桥梁，这一问题通常难于满足，从而给轨道结构受力和线型控制带来困难，需要针对具体问题进行理论研究。梁端变形作为一种特殊的非正常边界条件将直接影响相应区段轨道结构受力，对轨道几何形位、扣件受力、无砟轨道受力造成影响，进一步影响结构使用性能和行车安全，且后续处理较困难[7]。虽然新型有轨交通荷载较小，轴重较轻，但并不能因此而忽略这一问题。

2.1 线形控制要求

梁端发生位移时带动钢轨发生竖向上的位移，因此在梁体端部钢轨必然偏离原来设计位置，形成高低不平顺，该不平顺将影响列车通过时的舒适性，甚至影响运行的安全性，因此必须加以控制。研究表明，梁端位移影响的范围主要为梁缝附近5～6组扣件，钢轨的变形属于短波不平顺[8]。因此，采用10m弦进行测量时，其不平顺矢度不宜超过验收标准2mm，即本次检算时不超过4mm[5]。

2.2 轨道结构受力要求

（1）扣件上拔力。对于扣件来说，为保证扣件的使用安全，不允许出现弹性垫板失压现象，即梁端扣件附近上拔力F1应该满足式（3）要求。

式中：Ff0为扣件的扣压力；KP为轨下垫板刚度；Ks为单侧弹条刚度。为了实际工程应用方便，将上式简化为F1，max≤Ff0，即两侧扣件所受上拔力之和不能超过其初始扣压力。对于不同类型的扣件扣压力是不一样的，针对本文计算中的G型扣件而言，常阻力扣件系统单个弹条扣压力不小于11kN，弹程13mm，检算时认为Ff0=22kN；小阻力扣件系统单个弹条扣压力不小于8.4kN，弹程14.1mm，检算时认为Ff0=16.8kN[5、7]。

（2）扣件下压力。扣件下压力限值需考虑两个方面的因素：一方面，扣件下压力不应超过F1，max，即保证弹条不松动；另一方面，避免弹性垫板在列车荷载、梁端变形附加荷载等交变荷载下发生疲劳破坏。实际工程运用中，当扣件受到的下压力为（KP+2Ks）δs时，即扣件的压缩量达到弹条的弹程时，将出现弹条松动现象。参考德国标准《铁路桥梁和其他工程结构物规范》[（VEI）DS804]，为保证弹性垫板的使用安全，规定“在全部动荷载作用下，弹性垫板的最大压力作用下的弹性压缩量应不大于允许的下沉量[s]，下沉量[s]取值为2.5mm”。按照日本JRS对经常性荷载作用下垫层的平均压缩应力经常性荷载作用下的最大压缩应力、平均压缩变形的规定，弹性垫层压缩量不宜超过其厚度的20%。综合来看，对于12mm厚弹性垫层而言,其压缩量容许值取为2.4mm[5,7]。出于安全考虑，检算中取[s]=2.4mm。

（3）钢轨应力。梁端变形引起的钢轨纵向力产生的附加应力与《铁路无缝线路设计规范》（TB 10015—2012）中规定的轨底动弯应力、温度应力、伸缩或挠曲附加应力、制动应力之和不得超过钢轨强度容许限值，即

3 结果分析

为便于说明，定义图3模型中与纸面垂直靠外一侧（x值较大一侧）的钢轨为前侧钢轨，与纸面垂直靠里一侧（x值较小一侧）的钢轨为后侧钢轨，且定义结构受拉为正，受压为负。

3.1 最低温梁端优化前后位移与受力分析

最低温度下跨东平水道桥主桥小里程侧梁端优化前后的位移与受力情况如表1和图4所示。

由表1和图4可知，梁端未优化时轨道结构产生的高低不平顺矢度最大值发生在后侧钢轨15.103m处，最大高低不平顺矢度为28.397mm＞4mm；扣件所受最大拉力位于后侧钢轨距离15.589m处（常阻力扣件），最大拉力值为55826kN＞Ff0=22kN；扣件所受最大压力位于后侧钢轨位移14.964m处（常阻力扣件），所受最大压力为81140kN，其压缩量值为81140/50=1622.800mm＞2.4mm。由此可知，为保障线路运营时的安全性和舒适性，该梁端结构必须采取优化措施。

梁端优化后轨道结构产生的高低不平顺矢度最大值发生在后侧钢轨16.248m处，最大高低不平顺矢度为2.463mm＜4mm；扣件所受最大拉力位于后侧钢轨位移14.429m处（小阻力扣件），最大拉力值为16.347kN＜Ff0=16.8kN；扣件所受最大压力位于后侧钢轨位移15.029m处（小阻力扣件），所受最大压力为45.458kN，其压缩量值为45.458/40=1.136mm＜2.4mm。由此可知，该梁端在采用伸缩调节器进行结构优化后，各项控制指标均满足要求，使用伸缩装置结构能够对该桥梁主桥侧的梁端起优化作用，建议在设计及施工中考虑使用梁端伸缩装置结构。

3.2 最高温梁端优化前后位移与受力分析

最高温度下跨东平水道桥主桥小里程侧梁端优化前后的位移与受力情况如表2和图5所示。

由表2和图5可知，梁端未优化时轨道结构产生的高低不平顺矢度最大值发生在后侧钢轨15.103m处，最大高低不平顺矢度为18.191mm＞4mm；扣件所受最大拉力位于后侧钢轨距离14.964m处（常阻力扣件），最大拉力值为60337kN＞Ff0=22kN；扣件所受最大压力位于后侧钢轨位移15.589m处（常阻力扣件），所受最大压力为49480kN，其压缩量值为49480/50=989.600mm＞2.4mm。由此可知，该主桥梁端最高温情况下的受力变形同样无法满足线路运营时的安全性和舒适性要求，再次说明该梁端结构必须采取优化措施。

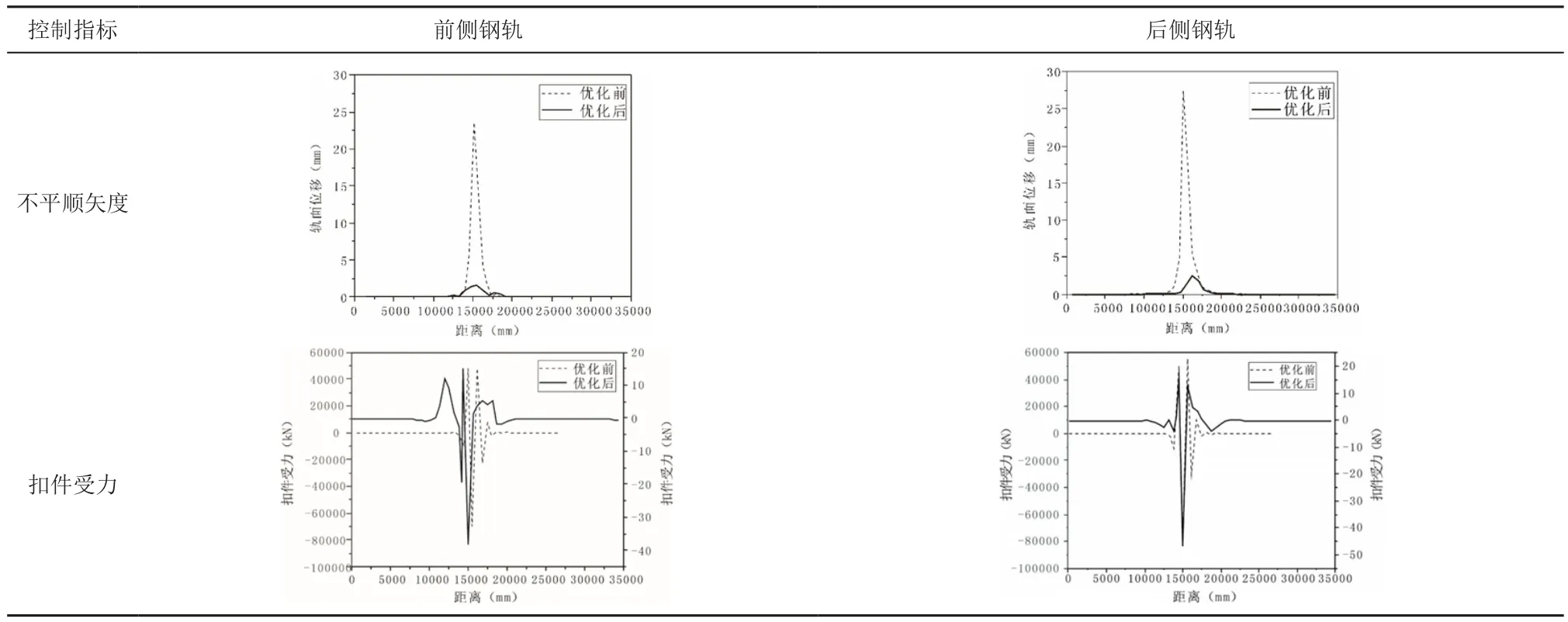
表1 最低温梁端优化前后位移与受力

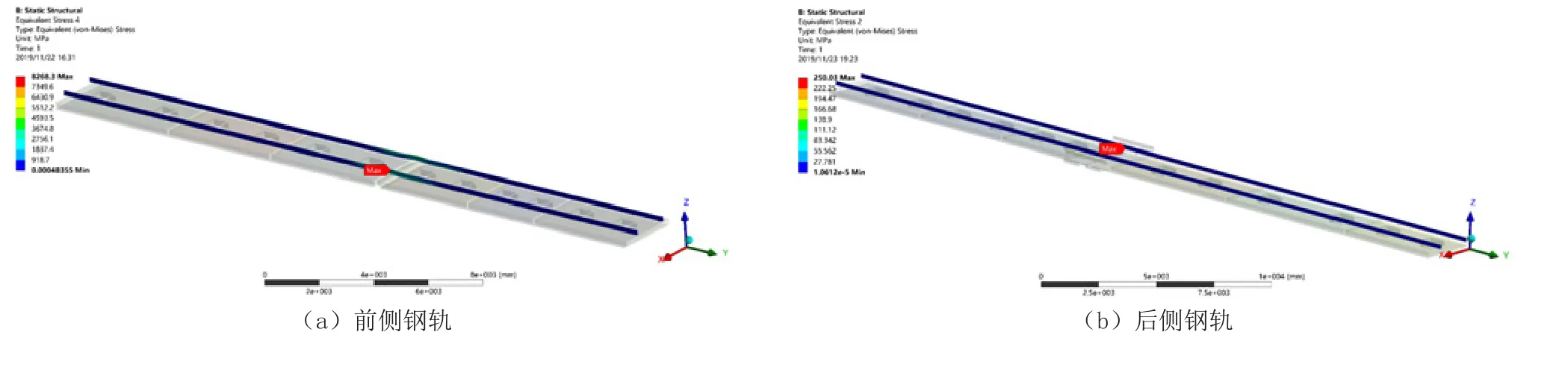
图4 最低温梁端优化前后钢轨应力

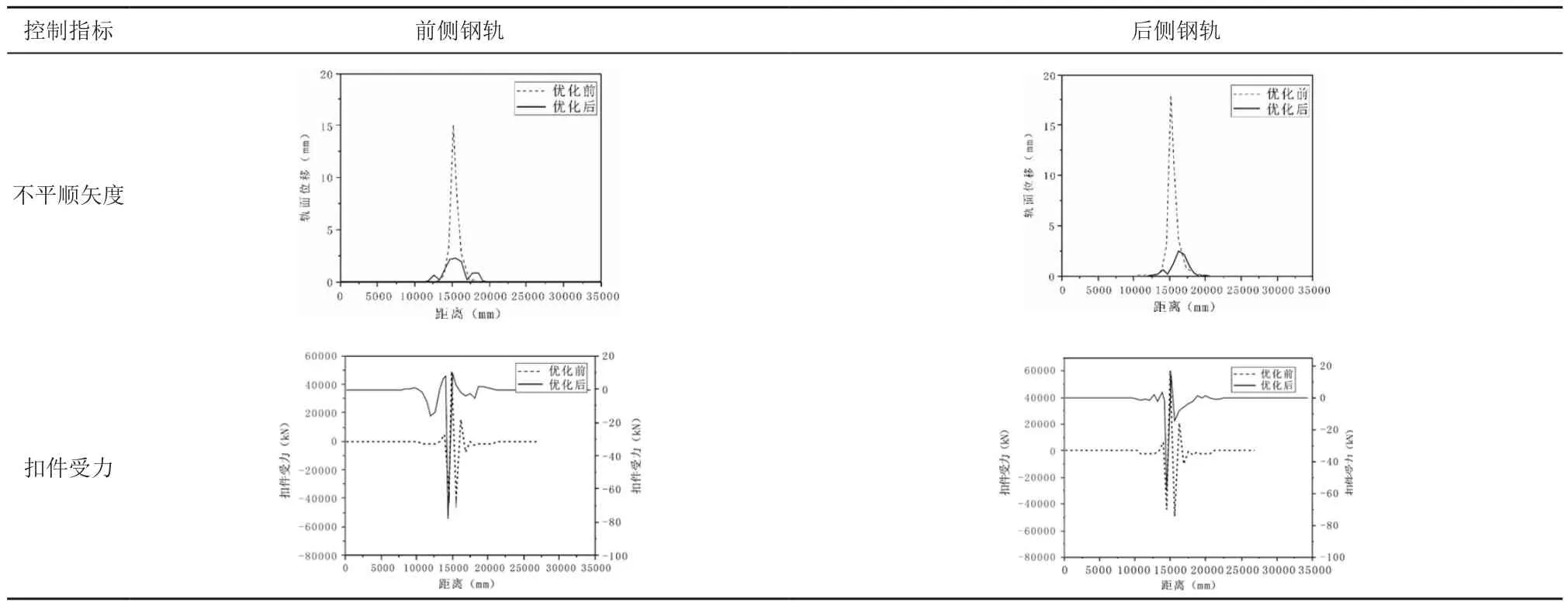
表2最高温梁端优化前后位移与受力

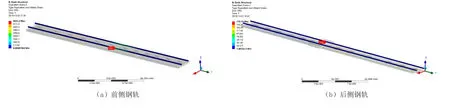
图5 最高温梁端优化前后钢轨应力

对该主桥梁端增设伸缩调节器优化后，轨道结构产生的高低不平顺矢度最大值发生在后侧钢轨15.510m处，最大高低不平顺矢度为2.464mm＜4mm；扣件所受最大拉力位于前侧钢轨位移15.029m处（小阻力扣件），最大拉力值为9.465kN＜Ff0=16.8kN；扣件所受最大压力位于前侧钢轨位移14.429m处（小阻力扣件），所受最大压力为78.048kN，其压缩量值为78.048/40=1.951mm＜2.4mm。由此可知，最高温条件下，该梁端在采用伸缩调节器进行结构优化后，各项控制指标均满足要求，使用伸缩装置结构能够对该桥梁主桥侧的梁端起优化作用，建议在设计及施工中考虑使用梁端伸缩装置结构[9]。

4 结论

通过对跨东平水道桥主桥梁端未优化和采用伸缩装置优化后的最低温度作用、最高温度作用工况下的梁端轨道结构受力计算与分析，可以得到以下结论：

（1）在重点考虑主桥小里程侧梁端未优化情况下，最低温度作用、最高温度作用等附加荷载时的梁端轨道结构扣件上拔力检算、扣件下压力检算、钢轨应力检算、不平顺矢度检算均有至少一项或多项不满足要求。

（2）该主桥梁端轨道结构如不采取优化措施，将可能无法满足最终运营时对于安全性和舒适性的相关要求。

（3）梁端采用伸缩装置进行结构优化后，考虑最低温度作用、最高温度作用等附加荷载情况时的梁端轨道结构扣件上拔力检算、扣件下压力检算、钢轨应力检算、不平顺矢度检算均满足要求。

（4）使用伸缩装置结构能够对该桥梁引桥-主桥梁端起优化作用，建议在设计及施工中考虑使用梁端伸缩装置结构。大里程端梁缝及错台值远小于小里程端梁缝及错台值，可参考小里程端伸缩装置结构，因地适宜地进行设置。