基于遗传算法的军队被装物资货位优化研究∗

（陆军勤务学院 重庆 401331）

1 引言

被装是军队装备的常服、礼服、作训防护服、标志服饰、卧具、装具的总称，是军人作战、训练、生活的重要物质基础[1]。货位优化是指给储存的各种物资分配合适的货位，使总体储存效益达到最优[2]。被装物资的货位分配问题影响着拣选效率和出入库效率，与被装保障水平紧密联系。货位优化以提升仓储作业效率和空间利用率、降低成本、增加货架稳定性为目标。因此，货位优化问题通常是多目标优化问题，需要通过建立数学模型，并运用算法求得最优解。本文将建立被装物资货位优化的模型，并使用遗传算法求解模型，得到最优的货位分配方案。

2 货位优化模型的建立

2.1 问题描述与条件假设

分配货位要遵循两条重要的原则[3～4]：1）周转率原则，将周转率高的物资安排在离出口较近的货位上。2）重心原则，考虑货架在垂直和水平方向上的稳定性，将重量大的物资储存在低层，在水平方向上的摆放也要尽量均匀。根据这两条原则，将优化目标定为缩短物资出库时间和增加货架稳定性，模型假设以自动化立体库为背景，但对于采用货架储存物资的普通仓库也有借鉴作用[5]。

现假设某座库房中有n排货架，每个货架有m列货格和l层，那么这座库房总的货位数为nml个 。 用 x，y，z（x∈[1 ，n]，y∈[1 ，m]，z∈[1 ，l]，x，y，z∈Z）分别表示货位所在的排、列、层，每个货位的坐标可以表示为（x，y，z），比如（2，5，6）就表示第2排第5列第6层的货位。此外，假设每个货位只存放一个托盘，每个托盘上只储存一箱物资。同时，为方便计算，忽略堆垛机在取货时伸缩机械臂所耗费的时间，且在每排货架的同一侧作业。一些涉及到计算的其他参数的假设情况如表1所示。

表1 各参数的值

2.2 建立模型

第一个优化目标是减少出库时间，在堆垛机运行速度一定的情况下，要减少出库时间就要缩短所有物资出库移动距离之和[6]。为了简化计算，假设只有一台堆垛机。堆垛机从原点（0，0，0）出发，先沿x轴方向水平运行，到达目标货位所在排时，进入巷道内沿y轴水平运行，到达目标货位所在列时，再沿z轴垂直运行，最终到达目标货位（x，y，z）。堆垛机在x轴方向运行时，要经过（x-1）个货格，同时考虑到每两排货架间的距离，即巷道的宽度为S0，假设堆垛机运行到巷道口中心位置再进入，则所经过的巷道数为（x-1-1/2）个。堆垛机进入巷道后，首先运行到目标货位所在列的第一层货格的底部中心位置，然后再开始上升。因此，在前往目标货位所在列的过程中，堆垛机要经过的货格数为（y-1/2）个。到达目标货位所在列后，堆垛机在上升过程中要经过的货格数为（z-1）个。堆垛机在水平方向和垂直方向上的运行速度分别为Vh和VV，因此货位坐标为（x，y，z）的物资从货位到出口的移动时间ti为

将货架上所储存的物资搬运到出口所耗费的总时间还与各种物资的周转率Pi有关，即，因此，物资出库效率优化的目标函数可表示为

第二个优化目标是提高货架稳定性。货架的稳定性由其垂直重心和水平重心决定，假设质量为G1、G2……Gn的物资被分别存放在高度为H1、H2……Hn的货位上，那么此货架的垂直重心位置为

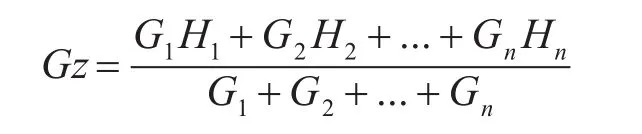
一个货格的重心通常在其几何中心，要使整个货架在水平方向上的稳定性达到最佳，就要尽量让其水平重心靠近水平方向的中心位置，即mL0/2（货架长度的1/2）处。因此，货架水平重心位置Gy可表示为

为了优化货架整体稳定性，要使Gz和Gy之加权和取最小值，假设两者的权重c1和c2均为0.5。综上，货架稳定性优化的目标函数可表示为

综上，建立货位优化的多目标模型如下：

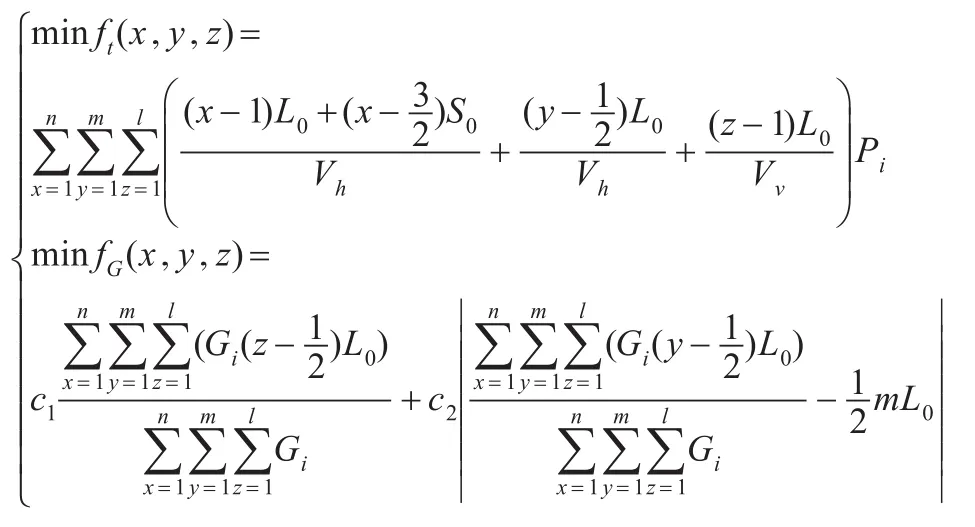
其中，1≤x≤n，1≤y≤m，1≤z≤l，且均为整数。

3 运用遗传算法求解模型

根据多目标优化问题的本质，各个目标函数之间是存在相互冲突的关系的，不存在使所有目标函数都达到最优状态的解，因此只能取得一组折中解，即帕累托最优解[7]。在解决多目标优化问题上，遗传算法具有独特的优势：1）可广泛地对可行解进行表示，直接对问题的结构对象进行操作。2）群体搜索。不同于许多传统的算法，遗传算法可以同时处理多个个体并对解进行评估。3）限制条件较少。遗传操作的基础是适应度函数值，不受函数连续性的约束。4）不易陷入局部最优，找到全局最优解的能力较强。因此，遗传算法适用于解决被装物资货位优化问题。

3.1 遗传算法基本原理

遗传算法（Genetic Algorithm，GA）是一种模拟生物的遗传和进化机制的自适应概率优化技术，这个概念最早在1967年由美国密歇根大学的学生Bagley首次提出，Bagley的老师Holland教授在1975年提出了遗传算法的系统论述。生物通过染色体的交叉和变异完成进化，遗传算法通过特定的编码方法产生“染色体”，并对“染色体”上的基因进行选择、交叉、变异，通过对个体进行评价筛选，最后找到最好的“染色体”。它从一个随机的初始种群出发，对其中的个体进行选择、交叉、变异，形成新一代种群。通过数次迭代，种群不断进化，最后收敛得到适应能力最强的种群，即得到问题的最优解[8]。遗传算法的主要运行步骤如下。

第一步，编码。确定所要解决的问题的变量及相关参数后，变量x即可作为个体的“表现型”，用特定的编码方式对x进行处理后得到的字符串即为它的“基因型”，编码就是表现型与基因型之间的映射，它是遗传算法识别个体的基础。例如，采用二进制编码方法时，将十进制数1850转化为二进制数11100111010的过程就是编码，十进制数是表现型，二进制数是基因型。

第二步，产生初始种群。随机生成n个初始个体，即特定的结构数据，可以是二进制串，也可以是实数结构，由这些个体构成初始种群。遗传算法以初始种群为起点进行迭代，迭代次数根据问题复杂程度确定，对于比较简单的问题，通常经过50至200次迭代就可找到最优解；对于一些很复杂的问题，迭代次数可达到数千次甚至上万次。

第三步，计算个体的适应度。适应度值表明个体的优劣程度[9]。将个体代入到目标函数中进行计算，得到目标函数值。通常目标函数是求得最小解，若优化问题的目标是求最小解，则无需转化。若优化问题的目标是求最大解，则需对目标函数值进行转化，获得个体的适应度值。

第四步，选择。根据个体的适应度值，通过特定的方法从当前种群中选择适应度值较高的个体，这些个体将成为父代参与产生子代个体。适应能力强的个体为下一代提供优良基因的概率更大，体现出了达尔文进化学说中适者生存的思想。

第五步，交叉。以设定好的交叉概率Pc对不同父代个体的染色体片段进行交换，这样子代个体将拥有父代个体的组合特性。交叉操作是将父代优良基因遗传给子代的关键，能提高种群的适应能力。

第六步，变异。以设定好的变异概率Pm对随机选中的个体的结构数据进行随机的改变，即对某个体染色体上随机位置的基因值进行改变，例如将二进制串11100111010中第3位上的1变异为0，其对应的表现型就由十进制数1850变成了1594。自然界中变异概率很低，但变异能增加种群基因的多样性。

经过上述操作后得到的群体进入下一次迭代，当迭代次数达到设定的上限值时，遗传算法终止，输出最适应的个体，得到最优解[10]。

3.2 货位优化的相关数据

以自动化立体库为例，选取其中一个区域的货架作为优化样本，在这个区域中有3排货架，每排货架有5列、6层。同时，选取10种品名的被装作为储存在这一区域货架上的物资，这10种被装物资的初始货位分配情况如表2所示。在这10种被装物资中，囊括了军服、军鞋、装具等多个品种，在周转率、重量方面跨度较大，具有很好的代表性，适于作为货位优化的样本。这些被装物资的初始货位是随机分配的。

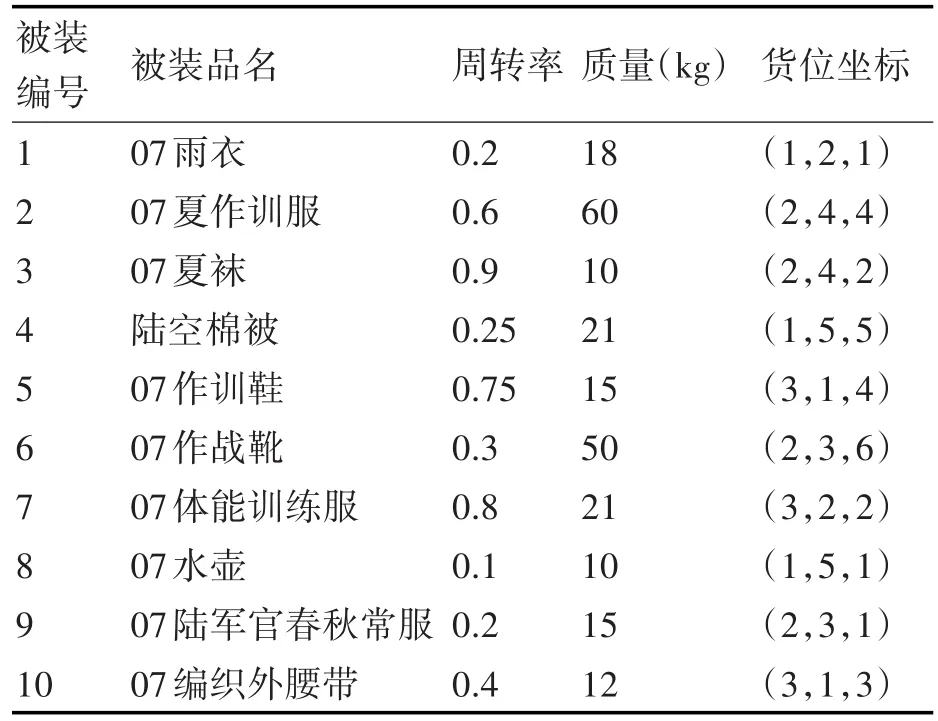
表2 被装物资初始货位分配情况

3.3 算法设计

1）编码。本文采用实数编码，一条染色体表示一种货位分配结果，从左至右依次包含一个货位的坐标、储存在该货位上的物资的周转率、物资的质量，其结构为xyzpiGi。例如，染色体1 2 1 0.2 18就是一个解，表示周转率为0.2，质量为18kg的被装品种被分配到坐标为（1，2，1）的货位上进行储存。

2）生成初始种群。确定编码方法就得到了个体的表示方法。染色体1 2 1 0.2 18代表一种货位分配结果，10条染色体组成一个个体，即一个包含全部10种被装物资货位分配结果的方案，初始种群就是由若干个个体组成的[11]。初始种群大小设定为50个，即随机产生50个货位分配方案。将x、y、z进行排列组合，产生n*m*l（n=3，m=5，l=6）种货位坐标，即90种货位坐标，将其储存在一个90×3的矩阵A中。然后，生成[1，90]之间的随机整数，取前10个数作为矩阵A的行向量序号，例如前10个数为 8，2，10，7，4，3，6，9，5，1，就取矩阵A的第8，2，10，7，4，3，6，9，5，1行为10种被装物资的货位坐标，与它们的周转率和质量结合起来，成为一个10×5的矩阵，每一个行向量代表一个货位分配结果，整个矩阵表示一个个体，这样就生成了一个初始个体：

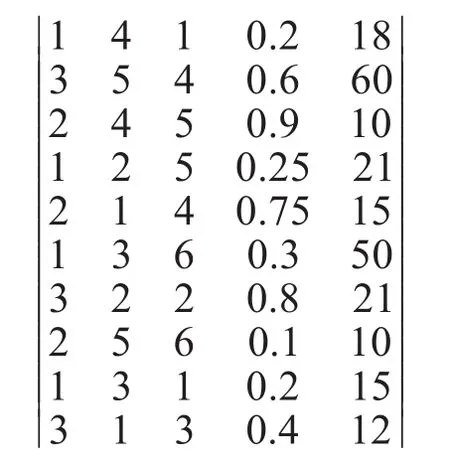
将这个方法循环运行50次，就得到了含有50个个体的初始种群。

3）计算目标函数。前文已建立了被装物资货位优化模型，可直接将个体代入模型进行计算，得到该个体的目标函数值。个体的目标函数值越小，则表示该个体适应度越大，即货位分配结果更优。

4）遗传操作。（1）选择：先使用RANKING函数对个体进行适应度值的分配，然后用根据适应度值大小FitnVi进行选择。若总共有u个个体，一个个体被选择的概率为

适应度值较大的个体可能被多次选择。（2）交叉：对当前种群中的个体进行重组，每个矩阵中奇数行和偶数行进行配对重组，得到新的个体。由于本文要解决的问题是组合优化问题，被装物资的周转率和质量是一一对应的，不能改变，因此只有它们的货位坐标进行交叉，本文把交叉概率pc设定为0.6。（3）变异：先将货位坐标转化为二进制数，再使用变异函数对其进行变异。变异完成后，再将二进制数转化为十进制数，获得变异后的货位坐标。

5）迭代。设定迭代次数为50，当上述操作完成一次后，进入下一次迭代，直到迭代次数满50次为止。在迭代过程中，目标函数会逐渐收敛，最后得到最优解。

4 使用Matlab运行遗传算法

以Matlab7.1作为实现遗传算法的软件，加载由英国谢菲尔德大学开发的遗传算法工具箱GAT⁃BX，这个工具箱中包含了实现遗传算法所需的多种函数，能够很好地解决多目标优化问题。将表1中的参数写入到一个M文件中[12]，编写被装物资货位优化问题的遗传算法程序，然后运行程序，得到货位优化结果并进行分析。

4.1 货位优化结果

运行Matlab程序，可获得模型的求解结果，包括各目标函数的最小值、模型的帕累托最优解、目标函数图像等。最优解如表3所示，其中的货位坐标是优化后的结果。效率优化目标函数在50次迭代过程中的图像如图1所示，其中，位于上方的曲线表示解的平均值的变化过程，下方的曲线表示最优解的变化过程。货架稳定性优化目标函数的图像如图2所示。

表3 优化后的货位分配情况

4.2 结果分析

由图1可以看出，迭代开始时，效率优化目标函数值最高处于22左右的水平。在运行到第1代和第10代之间时，函数值在19～22之间浮动。此后，函数值基本稳定在19左右，其平均值也呈明显下降趋势。从图2可以看出，目标函数值经过15次迭代，由17.9左右下降到17.4左右，此后基本收敛在17.4，其平均值也在18.1左右收敛。表4中列举了优化前后的货位分配方案的目标函数值，可以看出，效率优化目标函数值下降了29.9%，物资出库效率得到显著提升。同时，货架稳定性优化目标函数值下降了6.0%，两目标函数之和下降了20.1%，说明模型整体优化效果较好。

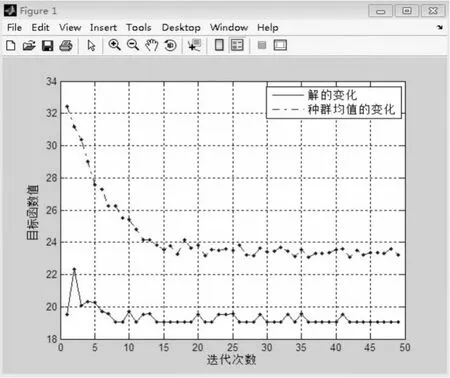
图1 效率优化目标函数迭代过程

图2 货架稳定性优化目标函数迭代过程

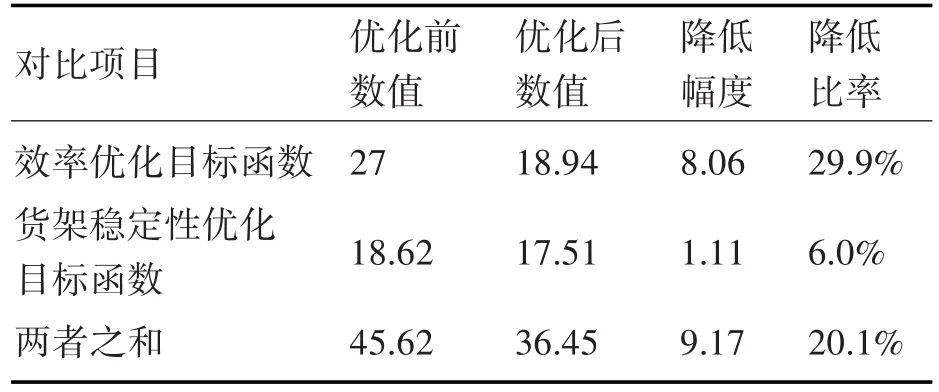
表4 优化前后效果比较

综上所述，遗传算法全局搜索、并行运算的特点使它能高效地求解多目标优化问题，并且能直观地展现出优化过程，具有很强的实用性。本文建立的被装物资货位优化模型基本达到了预期目标，在物资出库效率和货架稳定性两个方面取得了较好的优化效果。由此可见，根据货位分配原则设定明确的货位优化目标，建立相应的数学模型，然后运用适当的工具进行求解，根据实际情况将得到的优化结果进行调整和应用，就能取得储存规划的优化效果，提高被装仓储作业的效率。

5 结语

通过运用遗传算法在MATLAB中模拟被装物资货位优化，验证了这个多目标组合优化问题的一种有效解决方案，同时也为解决类似问题提供参考。物流行业正处在上升期，军事物流建设还有很长的路要走。要保障打赢未来战争以及保障非战争军事任务，军事物流信息化建设有至关重要的作用。互联网技术和人工智能发展迅猛，军事物流信息化建设也充满机遇。通过理念创新与技术融合，让军事物流信息化的进步为强军事业提供全方位的有力保障。