不同时间间隔下的道路交通状态判别
2020-06-18戴学臻苑仁腾王少玲吴智伟
戴学臻, 苑仁腾, 王少玲, 吴智伟
(1.长安大学 公路学院, 陕西 西安 710064;2. 河南鼎智工程咨询有限公司,河南 郑州 450000)
0 引言
随着汽车使用率的增加,交通拥堵问题困扰着每个大中小城市,其中这种现象在部分大城市中尤为突出,已经严重阻碍了城市的发展,影响了人们的出行,同时也给社会经济发展带来了巨大的损失。为解决城市拥堵问题,首先需要对交通的运行状况进行检测,及时辨别拥堵路段,以便采取合适的交通管理措施缓解交通拥堵。
由于交通状态具有模糊性和不确定性,因此部分学者多利用模糊数学的相关理论对道路交通状态进行了识别[1-4]。例如,孔祥杰等[5]以浮动车轨迹数据为基础,利用模糊综合评价法对道路交通拥堵状态进行了分析。诸云等[6]构建了城市道路交通运行状态评价指标体系,并利用模糊神经网络法对其进行了评价。当前利用模糊数学的相关理论虽然在一定程度上可以取得较好的评价效果,但是由于模糊数学本身的局限性,使得该方法仅刻画了道路状态隶属于交通拥堵的程度,不能表示隶属程度差异性和过渡性。例如交通运行状态水平处于3级时的速度区间为30~50 km/h,当两个路段的平均速度为49~31 km/h时,都被认为是道路交通运行状态处于3级服务水平,但却无法表现两个速度之间的差异性。
另一方面,当前对道路交通状态的评级指标主要有速度、流量、密度、占有率和平均延误等[7-10],如关伟等[11]依据不同密度下的速度分布特性,将城市道路交通流划分为4种状态;戴学臻等[12]以车辆平均行程车速、道路网延误时间比等作为判别指标,利用集对分析方法与三角模糊数进行耦合,构建了道路交通运行状态识别模型;姜桂艳等[13]通过分析拥挤的特征模式和各种数据挖掘技术的特点后,对偶发性拥堵和常发性进行识别。但是多数研究存在评价指标过多、数量大、数据获取难度高等问题,同时由于各个评价指标不是相互独立的,指标间内部存在较高的相关性,导致在评价过程中利用不同指标得到的结果基本一致,使得模型实用价值降低。
车速是反映交通流特性变化状况的一个重要指标,是人、车、路和环境等因素与交通流作用下所产生的结果[3]。众多的研究表明,利用速度作为交通状态的评价指标取得了较好的评价效果[14-18]。例如,李梅红等[15]利用路段平均速度、速度变化系数和低速行程时间比,建立了交通服务水平模糊综合评价模型。姜桂艳等[16]使用车牌识别数据的单车行程速度采集方法及区间平均行程速度采集方法,对交通拥堵的识别方法进行了研究。李晨朋等[17]提出利用公交车辆的实时速度对道路交通状态进行估计,并取得了良好的效果; 郝媛等[18]根据快速路车辆行驶速度的大小,将交通流划分为6种状态,并提出利用速度变化图寻找拥挤源头。部分研究发现,速度分布独立,能直接准确反映交通流状态[19]。基于以上分析,本研究提出以道路车辆行驶速度为识别交通状态等级的单一评价指标。
由于交通状态具有动态性,受各种因素的影响,在短时间内可能会发生两种或多种不同状态的转变,因此选择合适的评价周期至关重要,当评价周期过长时可能会忽略状态之间的转变[1]。当前多采用路段的平均速度对道路交通状态进行研究,但是由于划分评价时间过长,使得评价结果具有一定滞后性,不能及时反映当前道路交通状态,例如以5 min为1个时间段,只能用以反映前5 min内道路的交通状况,不具有实时性。但当划分时间较小时,评价结果容易受到车流波动性和系统误差的影响。
针对该问题,本研究从一个新的角度出发,提出以通过路段断面的车辆数来划分评价时间间隔(如以连续通过断面的10 veh所用的时间为1个阶段),使得评价时间间隔可以根据交通量变化而发生改变。例如,当路段交通量较大时,评价时间间隔相对较小,评价结果可以及时反映道路交通状态的变化;当道路交通量较少时,交通状态变化相对稳定,此时所确定评价的时间间隔相对较长。然后利用集对分析理论从同、异、反3个层次研究速度的变化特性,克服模糊综合评价理论仅从同一性角度评价的局限性,深入挖掘每个车速所蕴含的内在信息,研究不同评价间隔划分方式下交通状态的评价结果变化情况。
1 评价模型的构建
赵克勤先生在1989年提出的联系数学集对分析(Set Pair Analysis,SPA)方法[20],在不确定推理、数据评价、系统决策、医疗卫生等领域里都已有成功的应用[21-23]。集对分析理论利用联系数和差异度系数将宏观的确定量与微观的不确定量联系起来,通过构造一个不确定系统,实现不确定性与确定性的相互转化,从同、异、反[24]3个角度对不确定性进行研究。因此本研究基于集对分析理论,对路段的车辆速度特性进行深入挖掘,以提高评价结果的精确性。
1.1 构建集对
集对是指具有一定联系的两个集合所构成的对子,表达为H(A,B)[20],其中设A为评价指标样本值组成的集合,本研究表示路段车辆的瞬时车速;B为评价指标的评价标准集,根据《城市交通运行状况评价规范》(GB/T 33171—2016)[25], 按车辆的平均行程车速将交通状态划分为5个等级,如表1所示。

表1 城市道路交通运行状况评价标准Tab.1 Evaluation criterion for urban road traffic operation
注:Vkf为路段平均行程速度;Vf为路段自由流速度。
1.2 构建集对分析的评价模型
集对分析是根据一定的需要对组成集对的两个集合的关系进行研究,其中两个集合之间的特征函数被称为联系数,利用联系数不仅把两个集合的各种关系用一定的数学运算符联系起来,而且能同时刻画出两个集合的关系所在的状态和趋势。联系数越大,表示集合间的同一性(相同性)越强;联系度越小,表示集合间的对立性(相反性)越强[26]。以三元联系数为例,联系数的基本表现形式所示为:
μ=ai+bj+ck,
(1)
式中,μ为综合联系度;a,b,c为联系度分量,分别表示同一性、差异性和对立性,其中a+b+c=1;i为同一性系数,取值为1;j为差异度系数,取值在[-1, 1]之间;k为对立性系数,取值为-1。i和k取值固定,可以表现集对的确定性;j取值位于[-1,1]之间,用以表现集对之间的差异性; 有时i,j,k不取任何值,仅作为一种标记。
五元联系数是将三元联系数中的bj进一步划分,便可以得到基于集对分析理论的多元联系数[27],使得计算结果更为准确。五元联系数表达式为:
μ=ai+b1j1+b2j2+b3j3+ck,
(2)
式中,a,b1,b2,b3,k为联系度分量,表示该样本对1级至5级分类标准的联系度,其中b1,b2,b3为差异度分量;j1,j2,j3分别为偏同差异度、中差异度、偏反差异度。
速度为效益型指标[28]。各等级联系数表达式为:
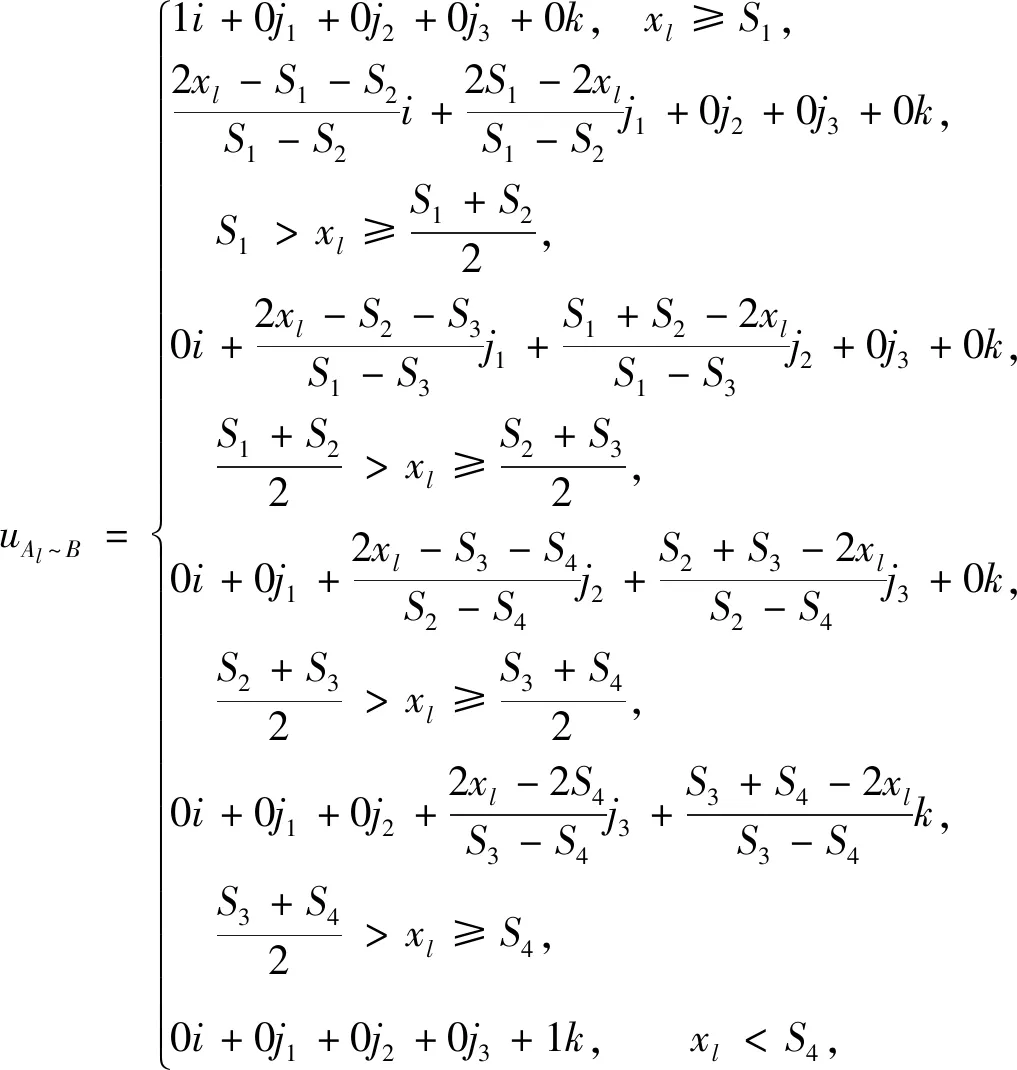
(3)
式中,uAl~B为集对H(A,B)中第l个样本的联系数;S1,S2,S3,S4为评价指标的界限值;xl为第l个样本的速度值。
取连续经过某断面的n辆车速,作为该时间段内的道路交通状态评价样本,则利用所得到的每个样本的联系数,可计算综合联系数:
(4)
式中,μy为y时刻道路交通状态的综合联系数;n(n≥1)为y时刻内取得样本的个数,其中当n=1时,表示计算每辆车的速度的联系数;am和cm分别为第m个样本的同一性和对立性系数;b1m,b2m,b3m分别为第m个样本的偏同、中和、偏反差异度系数。
1.3 评价等级的划分
当前多数集对分析研究都采用置信度准则[28-29]来判断评价对象所属级别,置信度准则原理可表达为:
hl=(f1+f2+…+fl)>λ(l=1, 2,…, 5),
(5)
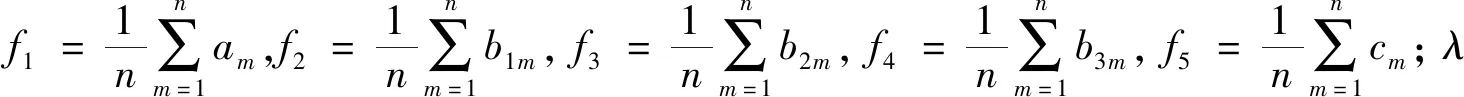
(6)
式中,d为评价等级;fi和fj分别为属于第i个等级和第j个等级的属性测度值。
2 案例分析
为验证模型的有效性,选择某路段为评价对象,其中该路段限速为70 km/h(Vf=70 km/h),分别采用传统模糊评价法和集对分析法对道路状态进行识别。
2.1 数据的获取
在路端人行天桥上设置调查站点,利用雷达测速枪记录来往车辆的行驶速度,车流方向取为由西至东。在2019年1月21日(星期一)16:30—19:30对该点的车辆行驶瞬时车速进行调查。每5 s记录1 veh驶过的车速值,共获得2 160 veh车的瞬时车速。从调查站点获得的车辆离散速度如图1所示,利用MATLAB软件对调查速度做去噪处理,处理结果如图2所示。
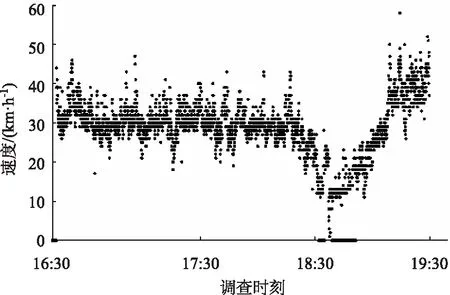
图1 路段内车辆行驶的离散速度Fig.1 Discrete speeds of vehicles in road section
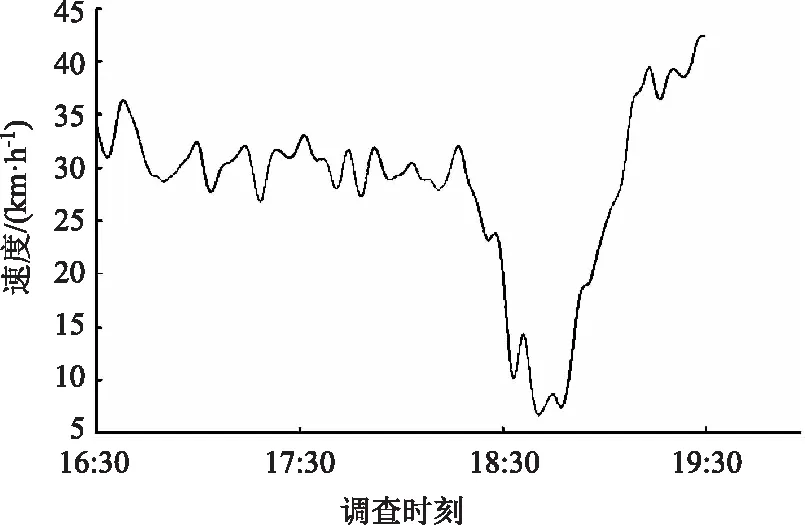
图2 除噪后调查时间内速度变化Fig.2 Speed change during investigation after denoising
因为评价路段的限速为70 km/h(vf=70 km/h),构建集对划分标准限值S1,S2,S3,S4分别为49, 35, 28, 21 km/h。
2.2 交通状态评价
由于n的取值不仅受路段交通量的影响,而且由于车辆行驶速度的波动性及调查设备的误差,均可能对评价结果产生一定影响。本次调查时间为晚高峰时段,道路交通量约为3 600 pcu/h。为了比较不同的时间划分方法对道路交通状态评价的影响,本研究依次取n=60,36,24,12,6和1,分别将交通状态划分为36,60,90,180,360和2 160个时间段,分别利用MATLAB软件求解式(6)~(7)。其中n=60和36时, 分别表示以5 min和3 min为1个时间段,依次取60 veh和36 veh车的瞬时车速作为该时间段的平均车速,计算得到的各时间段的综合联系数如表2和表3所示。
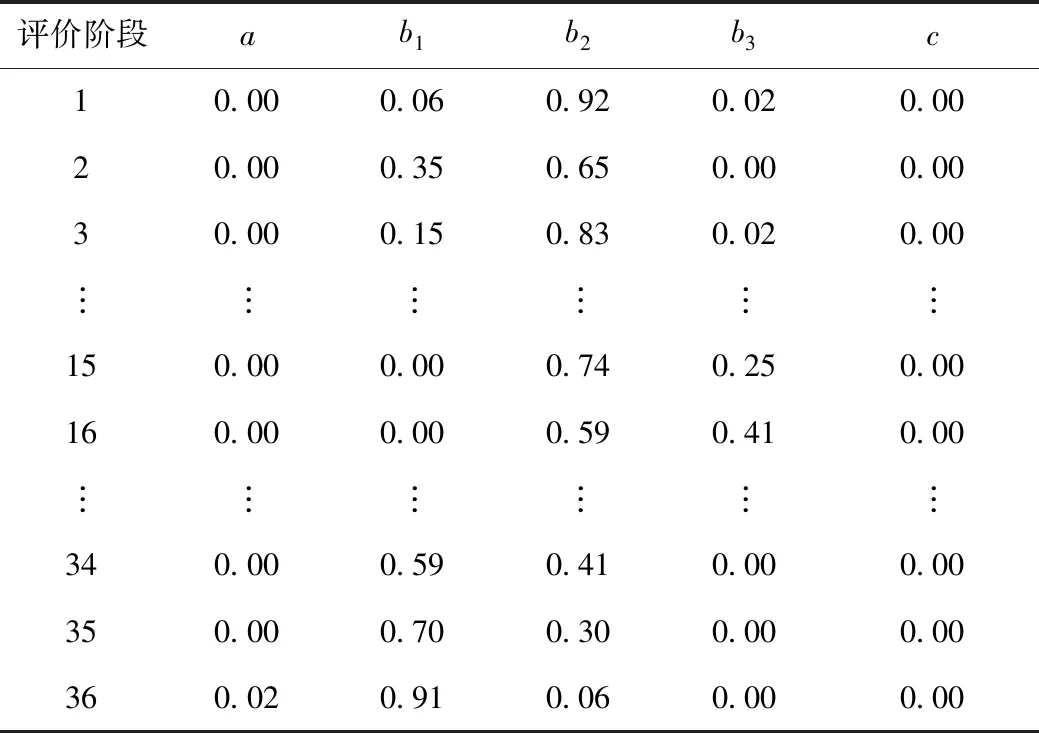
表2 各阶段的综合联系数(n=60)Tab.2 Comprehensive connection numbers for each stage (n=60)
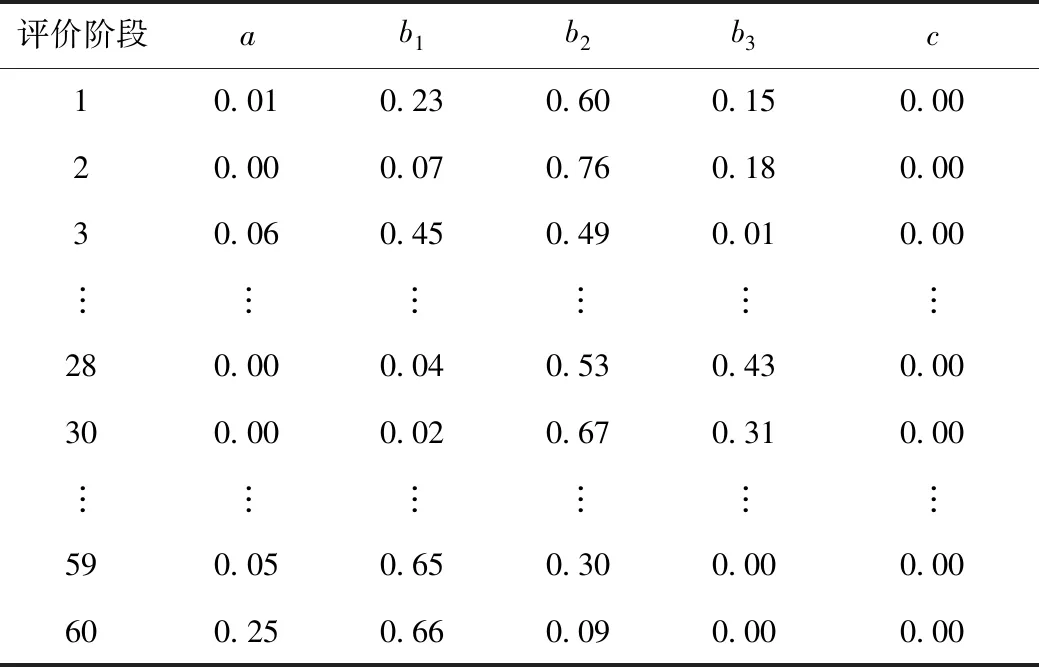
表3 各阶段的综合联系数(n=36)Tab.3 Comprehensive connection numbers for each stage (n=36)
置信度λ取0.7,由式(8)和式(9)可判别出各交通状态的级别, 结果见表4和表5。
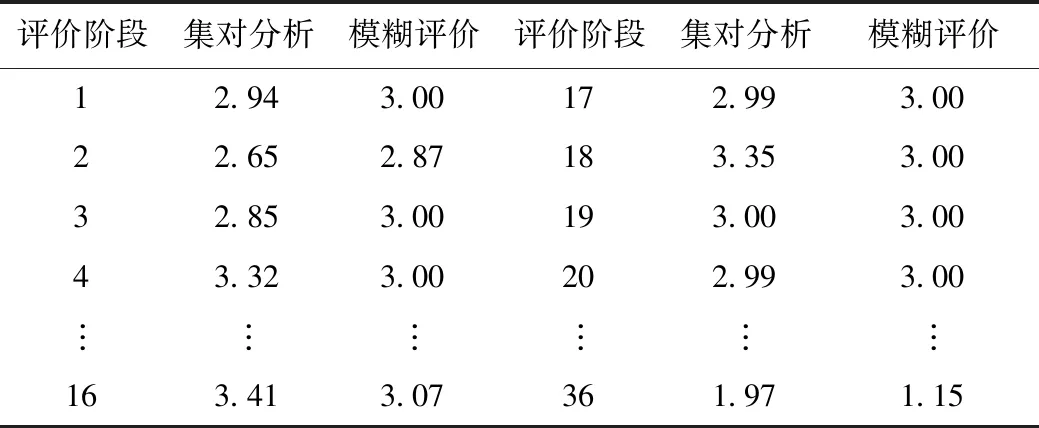
表4 各阶段的综合联系数(n=60)Tab.4 Comprehensive connection numbers for each stage (n=60)
当n=24,12,6,1时,分别表示以2,1,0.5 min 和5 s间隔划分时间段,依次取24, 12, 6, 1 veh 车的瞬时车速作为该时间段的平均车速,详细评价数据从略。将n取不同值的评价结果进行对比,如图4所示。
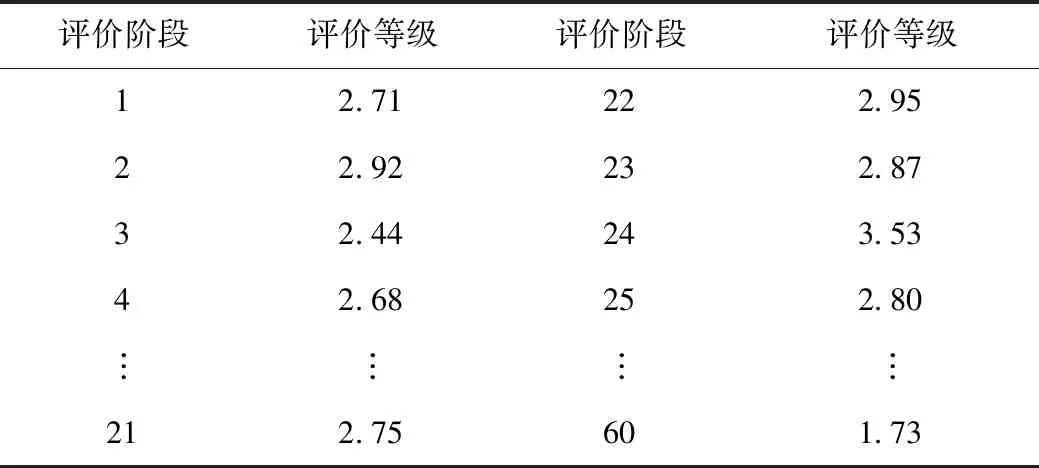
表5 各阶段的交通状态等级(n=36)Tab.5 Traffic status level of each stage (n=36)
由图3可知,6种划分方式下交通状态评价结果的变化趋势基本一致。由图3(a)~(c)和图3(f)可知,n值越小,交通状态的变化越敏感;由图3(d)和图3(e)可知,当n取12,6,1时,交通状态的评价结果基本一致。根据以上分析,对道路交通状态进行评价时,时间间隔划分得越小,评价结果与速度的变化越敏感;但当n<12时,即当划分时间间隔小于1 min时,交通状态的评价结果将不再受划分时间间隔的影响。因此在对道路交通状态进行评价时,评价时间间隔越小,对评价指标变化的敏感性越强,评价结果越接近于实际;但当评价时间间隔达到一定数值时,如本研究的n=12(1 min),此时交通状态变化的敏感性不再受划分时间间隔的影响。
由于交通状态的变化具有过程性,不会发生突然的增长或降低,因此利用高斯平滑滤波器对n=12时的评价结果进行优化,优化结果如表6和图4所示。
为了证明方法的有效性,分别采用集对分析法、模糊评价法对交通状态进行评价。根据上面的分析,集对分析法中n取12,以1 min为1个时间段,将16:30—19:30划分为180个评价时间段。模糊评价法的隶属函数为梯形函数,其中畅通状态、一般拥挤和严重拥挤分别对应本研究的1级、3级、5级交通状态。利用高斯平滑滤波器对集对分析评价结果做平滑处理,将模糊评价结果与集对分析评价结果进行对比,如图5所示。
由图5可知,两种方法的评价结果基本相同,但是与模糊评价法相比,本研究构建的模型对交通状态的变化反应更为灵敏,评价曲线更为平滑,可以更好地反映交通状态转变之间的过程性,表明了该方法具有一定的优越性。
3 结论
将集合A(实测数据)与集合B(判别指标标准构成)构成集对H(A,B),建立了基于五元联系数的城市道路交通状态评价模型,对比分析了不同时间间隔下道路交通状态评价结果的区别。研究发现,当划分评价阶段越小时,交通流量状态的敏感性越强,当评价阶段过小时(<1 min),交通状态的评价结果将不再受划分时间间隔的影响。以西安市某路段实测数据为例,分别利用模糊评价和集对分析对道路交通状态进行了识别,证明了模型的优越性。虽然本研究提出以车速作为划分评价间隔,但由于受到调查设备的限制,按照平均每5 s调查1种车速,与实际情况存在偏差。理想状态下,应记录每辆车辆的速度,并利用该方法对道路交通状态进行评价。在进行交通网络交通状态评价时,该方法应以路段为基础,考虑每条路段在交通网络中所处的权重,通过综合加权法评价区域网络的交通状态。
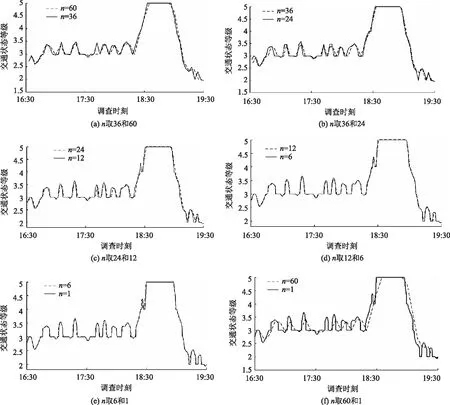
图3 n取不同值时的交通状态评价结果Fig.3 Traffic condition evaluation result with different n values
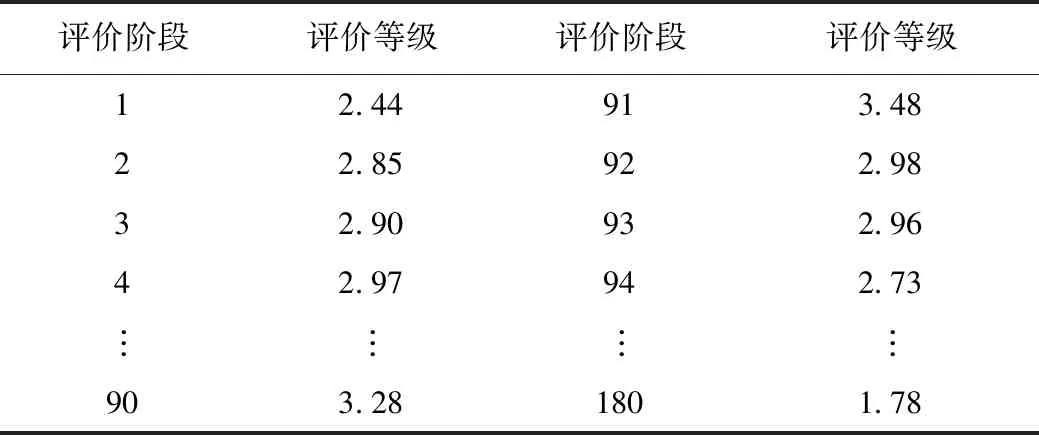
表6 利用高斯平滑滤波器对评价结果的优化结果(n=12)Tab.6 Optimized evaluation result by Gaussian smoothing filtering (n=12)
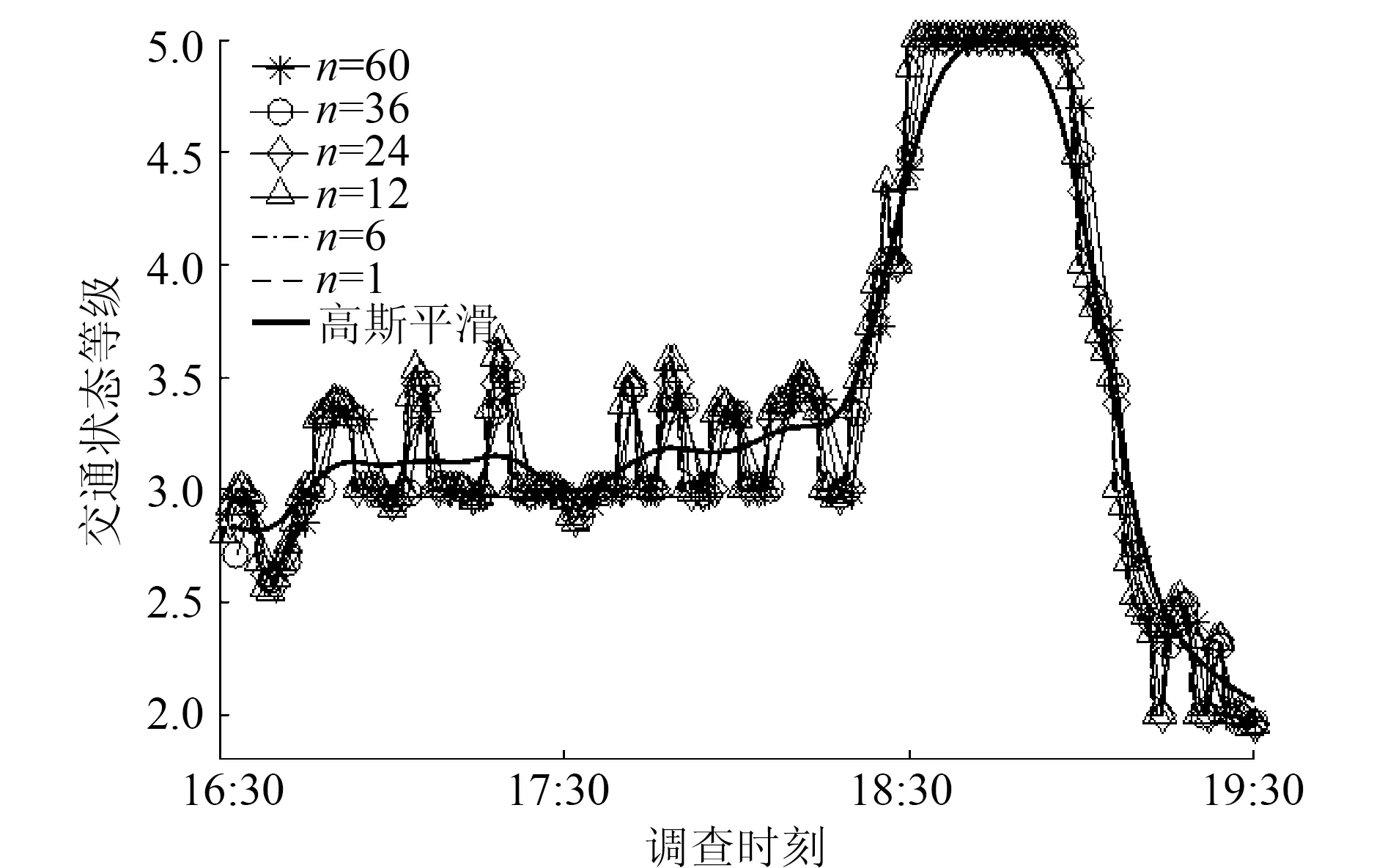
图4 交通状态评价结果优化Fig.4 Optimization of traffic condition evaluation result

图5 模糊评价与集对分析评价结果对比Fig.5 Comparison of fuzzy evaluation and set pair analysis
