基于EEMD-ACS-SELM 的弃风电量组合预测模型

2020-06-18谢丽蓉崔传世梁武星包洪印

可再生能源 2020年6期

张浩，谢丽蓉，崔传世，梁武星，包洪印

（1.新疆大学电气工程学院，新疆乌鲁木齐 830047； 2.特变电工新疆新能源股份有限公司，新疆乌鲁木齐830011； 3.中船重工海为（新疆）新能源有限公司，新疆乌鲁木齐 830000）

0 引言

近年来，新疆地区弃风问题备受关注，有关数据显示，2016 年新疆地区弃风电量为137 亿kW·h，占全国弃风电量的27.6%[1]，位列全国第一。为解决持续已久的弃风问题，国家发改委和能源局等部门先后采取一系列措施，使得2017 年和2018年全国的弃风现象在一定程度上得到缓解。但2017 年和2018 年新疆地区弃风电量占全国弃风电量的比重却为31.6%和38.6%[1]，呈逐年上升趋势，因弃风现象造成的经济损失十分严重。如何精确预测弃风电量，对提高新疆地区风电场经济效益和维护电力系统稳定具有重要意义。

目前，国内外学者对于弃风预测的研究还不是很多。文献[2]提出了一种机舱风速法计算风电场理论功率及弃风电量。文献[3]提出了一种基于经验模态分解和马尔科夫链的弃风电量预测方法。文献[4]研究了基于弃风特性的风电供热项目节煤效果与最佳配置方案。文献[5]提出了一种基于GRU-NN 模型的短期电力负荷预测方法。文献[6] 提出了一种基于EEMD-HS-SVM 的短期风功率组合预测模型。文献[7]提出了一种基于SVM 的风速混合预测方法。文献[8]为解决变速器阻塞管理问题，提出了能量存储系统平衡变异性的有效机制。文献[9]基于模型预测控制理论，提出了一种风电集群有功功率多时间尺度协调调度方法。总体而言，国内外的研究机构多关注于负荷预测、弃风消纳及风速、风功率预测的研究，而且均取得了重要的研究成果。但针对弃风现象严重的新疆地区，对于弃风电量预测的研究还较少。

为了对新疆达坂城某风电场的弃风电量进行准确预测，本文提出一种基于集合经验模态分解（EEMD）和t 分布自适应变异布谷鸟算法（ACS）优化改进极限学习机（SELM）的弃风电量组合预测方法（EEMD-ACS-SELM）。仿真结果表明，该方法对于风电场弃风电量的预测精度较高。

1 基于EEMD-ACS-SELM 算法的预测模型总体架构

1.1 弃风电量模型

风电场理论可发电量而实际未发出的电量称为弃风电量，一般将风电场理论发电量与实际发电量的差值作为风电场弃风电量。

式中：Wc为风电场弃风电量；Wt为风电场理论发电量；Wa为风电场实际发电量。

弃风电量不包括由风机自身设备故障损失的电量[2]。

图1 为弃风电量原理图。

图1 弃风电量原理图Fig.1 Wind power curtailment schematic diagram

计算Wt比较成熟的方法是样板机法，通过风速与风机出力的映射关系可以计算出单台样板机的理论发电量（Wti）。

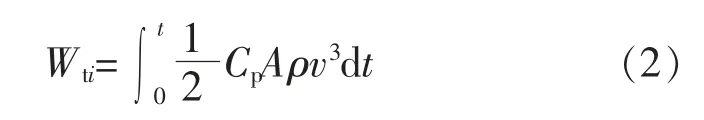
式中：Cp为叶片的功率系数；A 为叶片扫掠面积；ρ为空气密度；v 为风速；t 为采样时间。

Wt为Wti均值与同类型机组台数的乘积，即：

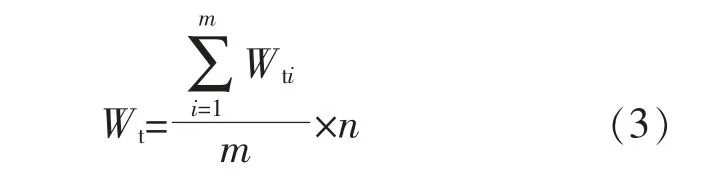
式中：m 为风电场样板机台数；n 为风电场同类型机组台数。

Wa可以从风电场管理系统中获得，利用式（1）可计算出Wc。

1.2 集合经验模态分解

1.2.1 经验模态分解

经验模态分解（EMD）是将原始时间序列分解成一系列不同频率的本征模态函数（IMF）和一个余项rn（t）的和。

在实际应用中，对弃风序列{Wc（t）|t=1，2，…，T}的分解方法如下。

①确定原始弃风电量序列Wc（t）的所有局部极值，采用3 次样条差值法拟合出Wc（t）的上下包络线u（t）和v（t），并计算平均包络线值m（t）：

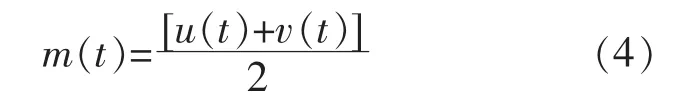
②令h（t）=Wc（t）-m（t），判断h（t）是否满足IMF 条件[10]，如果是，h（t）为Wc（t）的第1 个IMF分量，执行步骤④，否则，执行步骤③。

③将h（t）作为原始序列Wc（t），重复k 次步骤①和步骤②，直到满足终止标准，得到第1 个IMF 分量。

④将Wc（t）与第1 个IMF 分量相减，得到差值序列r1（t）：

⑤将r1（t）定义为新的Wc（t），重复步骤①～③得到第2 个IMF 分量，如此循环往复，依次获得各IMF 分量及最后一个rn（t），rn（t）为一个单调函数。

式中：Fi（t）为各IMF 分量。

1.2.2 集合经验模态分解

由于原始信号存在各种干扰，使得在经验模态分解过程中极易出现模态混叠现象，为解决这个问题，Wu Z[11]提出了集合经验模态分解方法（EEMD），该方法改进过程如下。

①在原始弃风序列中添加高斯白噪声序列εm（t），得到混合序列Wc，m（t）：

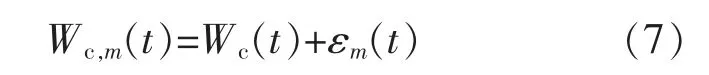
②对混合序列进行EMD 分解，分解得到n个不同频率的子序列和残余序列。

③采用不同量级的高斯白噪声重复步骤①和②100 次，得到一系列的子序列cim和残余序列rm。

④将100 次分解得到的子序列cim和残余序列rm分别求均值，即：

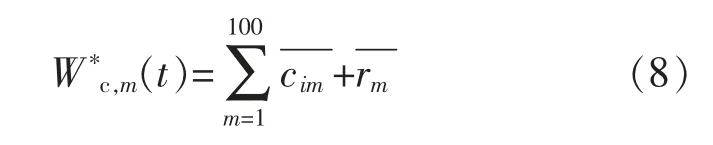
1.3 改进激活函数的极限学习机

1.3.1 极限学习机

极限学习机（ELM）是一种新型单隐层前馈神经网络算法，相比于传统BP 神经网络，具有学习速度快、泛化能力强等优势。因此，本文利用ELM对EEMD 分解后的IMF 分量进行预测。

假设：输入训练集有n 个变量，分别为W*c，m（t1），W*c，m（t2），…，W*c，m（tn），对应历史弃风电量；输出训练集为y，对应下一时刻弃风电量；g 为ELM 隐层神经元的传递函数；aij为输入权重；bj为隐层节点偏置；βj为输出权重。

ELM 算法步骤如下。

①给定输入训练集W*c，m（t1），W*c，m（t2），…，W*c，m（tn）和输出训练集y，隐含层节点个数为L，激活函数g（·）。

②随机初始化网络aij和bj。

④根据下一时刻的弃风电量值，即输出训练集y，通过β=H+y 计算输出权重βj。

⑤通过下式计算弃风电量的预测值。

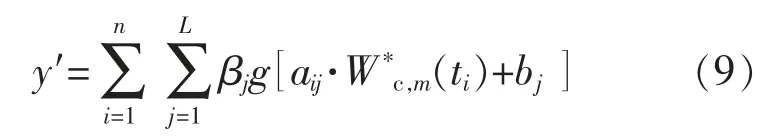
1.3.2 改进极限学习机

激活函数在ELM 网络中的地位至关重要，良好的激活函数能明显提高ELM 的泛化能力和精确度。文献[12]提出了一种具有一定稀疏能力且更接近生物学模型的Softplus 激活函数，相比于Sigmoid 函数，Softplus 激活函数提升了算法的平均识别性能。因此，本文选用Softplus 函数作为ELM 的激活函数，其函数定义为

1.4 t 分布自适应布谷鸟算法

1.4.1 布谷鸟算法

布谷鸟搜索算法（CS）是由Yang X S[13]提出的一种新型智能优化算法，根据布谷鸟寄生育幼的特点和莱维飞行的觅食方式来解决最优化问题。

布谷鸟位置变化及搜索鸟巢的路径为

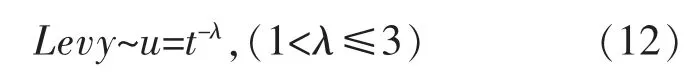
式中：λ 为幂次系数。

1.4.2 改进的布谷鸟算法

由于CS 算法的步长和发现概率被设成定值。步长太大，搜索精度降低，不易收敛；步长太小，搜索速度降低，易陷入局部最优。因此，本文采用文献[14]中提出的t 分布自适应变异算法对其改进。

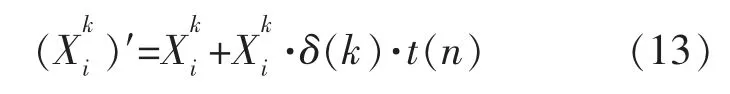
式中：t（n）为自由度为n 的t 分布；δ 为变异尺度因子。

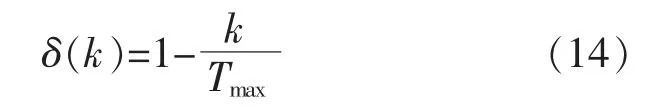
式中：Tmax为最大迭代次数；k 为当前迭代次数。

自由度n 的选取借鉴文献[14]中实验效果最好的算子t1，t1.5，t2，t2.5，t3，t20+k（k 为迭代次数），将各算子产生不同的个体根据适应度值进行比较，较优的进入下一轮进化。

2 EEMD-ACS-SELM 弃风电量预测模型建立

由于弃风电量具有间歇性和波动性，本文构建一种基于EEMD-ACS-SELM 的组合预测模型，流程图如图2 所示。

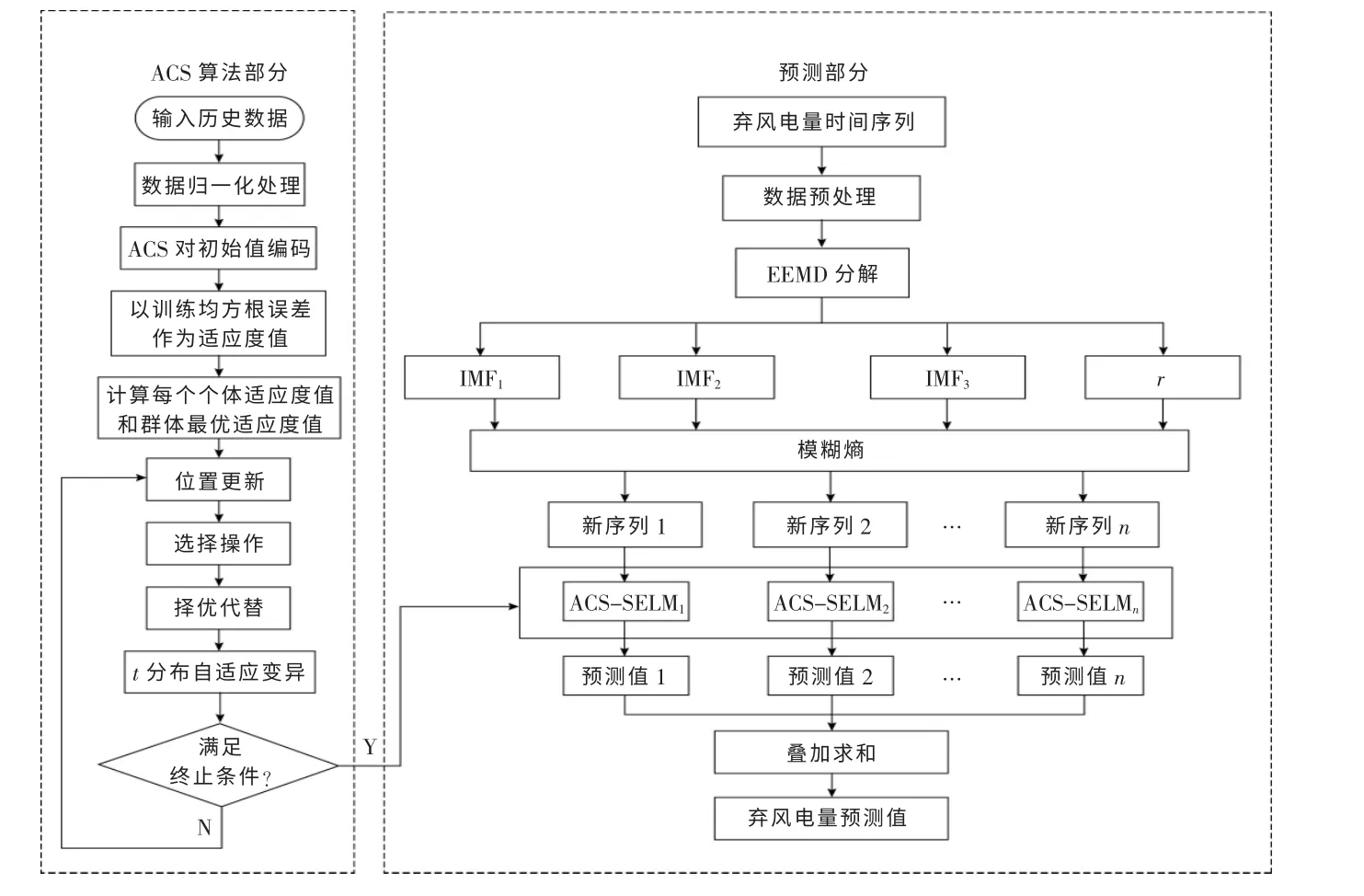
图2 EEMD-ACS-SELM 弃风电量预测流程图Fig.2 EEMD-ACS-SELM wind power curtailment

具体的预测步骤如下。

①将风电场采集到的数据预处理，利用式（1）得到原始弃风序列Wc（t），将其分为训练集和测试集并归一化处理。

②对弃风序列Wc（t）进行EEMD 分解，得到一系列不同频率的分量，计算各分量的模糊熵值，对模糊熵值近似的分量进行聚类。

③初始化种群规模n、最大迭代次数Tmax、发现概率fa和隐含层个数L 等，随机初始化n 个鸟巢初始位置Xi，i=1，2，…，n，每个鸟巢位置对应一组SELM 初始权值和隐含层偏置。

④以训练样本的均方根误差为目标函数，求得迭代过程中每个个体适应度值、群体最佳适应度值及对应的最佳鸟巢位置。

⑤利用式（11）对所有鸟巢位置更新，计算新的适应度并与历史记录中的适应度值比较，若新的适应度值较好，则用新鸟巢位置取代旧鸟巢位置。

⑥设随机数R∈[0，1]是寄生蛋被宿主发现的概率，将R 与fa相比，保留不易被发现的鸟巢位置，随机改变较易被发现的鸟巢位置，并和之前的鸟巢位置相比较，用较好位置代替较差位置。

⑦将新鸟巢位置按式（13）和（14）进行t 分布自适应变异操作，从中选择适应度值最优的一组鸟巢位置，与变异前位置进行对比，保留较优鸟巢位置，进入下一迭代。

⑧判断算法是否满足终止条件，若是，执行步骤⑨，否则，返回步骤⑤。

⑨终止搜索，将最佳鸟巢位置Xbest对应的参数作为SELM 算法最优输入权值和偏置，对聚类后的新序列分别建立ACS-SELM 预测模型，并将各序列预测值叠加求和，获得弃风电量预测值。

3 案例分析

为验证EEMD-ACS-SELM 模型的有效性，选取新疆达坂城某风电场2018 年6 月的弃风电量数据进行实例仿真验证（该风电场有25 台2 MW风机）。数据采样时间为15 min，对数据进行小时平均处理，共得到720 个数据。以1 h 为采样周期，风电场理论发电量、实际发电量及弃风电量曲线如图3～5 所示。取前696 个数据作为训练样本，后24 个数据作为测试样本，仿真软件为MATLAB2016b。

图3 理论发电量Fig.3 Theoretical power generation

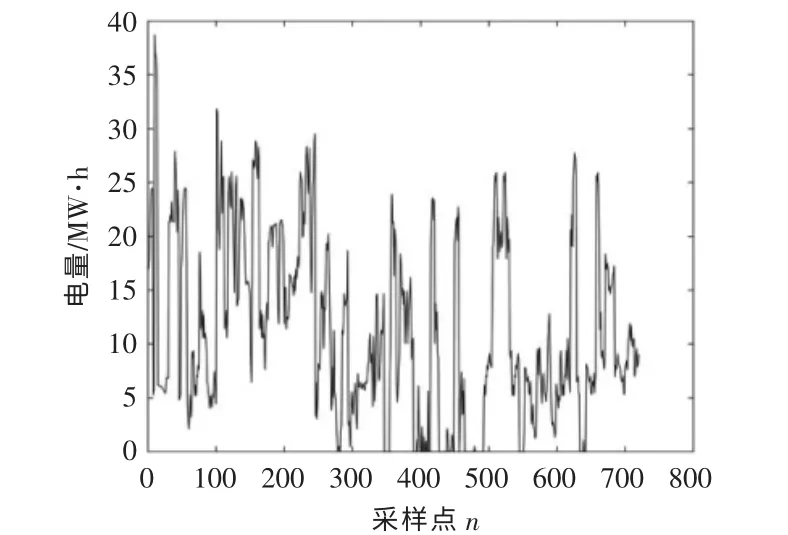
图4 实际发电量Fig.4 Actual power generation

图5 弃风电量Fig.5 Wind power curtailment

3.1 基于EEMD 的弃风电量多尺度分解

按照EEMD 分解步骤，对弃风电量时间序列进行分解，结果如图6 所示。

由图6 可知，经过EEMD 分解后得到8 个分量和1 个余项，在分解的过程中振动幅度逐渐降低，振动周期逐渐变长，各分量中包含着原始弃风序列中不同特征的信息。

3.2 模糊熵值聚类

由于EEMD 分解得到的分量较多，为降低预测模型复杂度，计算各个IMF 分量的模糊熵值，并对模糊熵值近似的分量进行聚类[15]。各IMF 分量的模糊熵值如图7 所示。

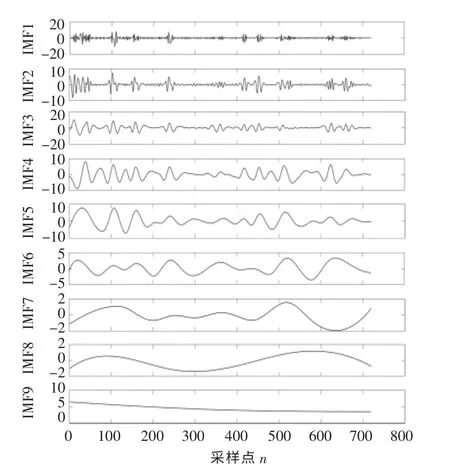
图6 弃风电量序列的集合经验模态分解结果Fig.6 EEMD results of wind power curtailment sequence

图7 各分量的模糊熵值Fig.7 Fuzzy entropy values of each component

由图7 可知，IMF 分量的模糊熵值随频率降低单调递减，各分量模糊熵值之间存在近似关系，对模糊熵值近似的分量进行聚类，结果见表1。

表1 新序列聚类结果Table 1 New sequence combined results

3.3 模型参数设置及各分量预测结果

本文进行超前3 步的弃风电量预测，预测结果为超前3 h 的弃风电量预测曲线。

在ACS 算法中，鸟巢规模为30，fa为0.25，最大迭代次数为200。在SELM 算法中，输入节点为12，输出节点为1。为确定新序列预测模型的最佳隐含层节点数，通过递增隐含层个数对网络进行训练，选择训练误差最小的节点数作为该序列最佳隐含层节点个数，序列1~5 的最佳隐含层节点数分别为26，22，29，27 和25。各序列预测结果如图8 所示。由图8 可知，建立的预测方法能较准确地反映各序列的变化趋势，取得了较好的预测结果。

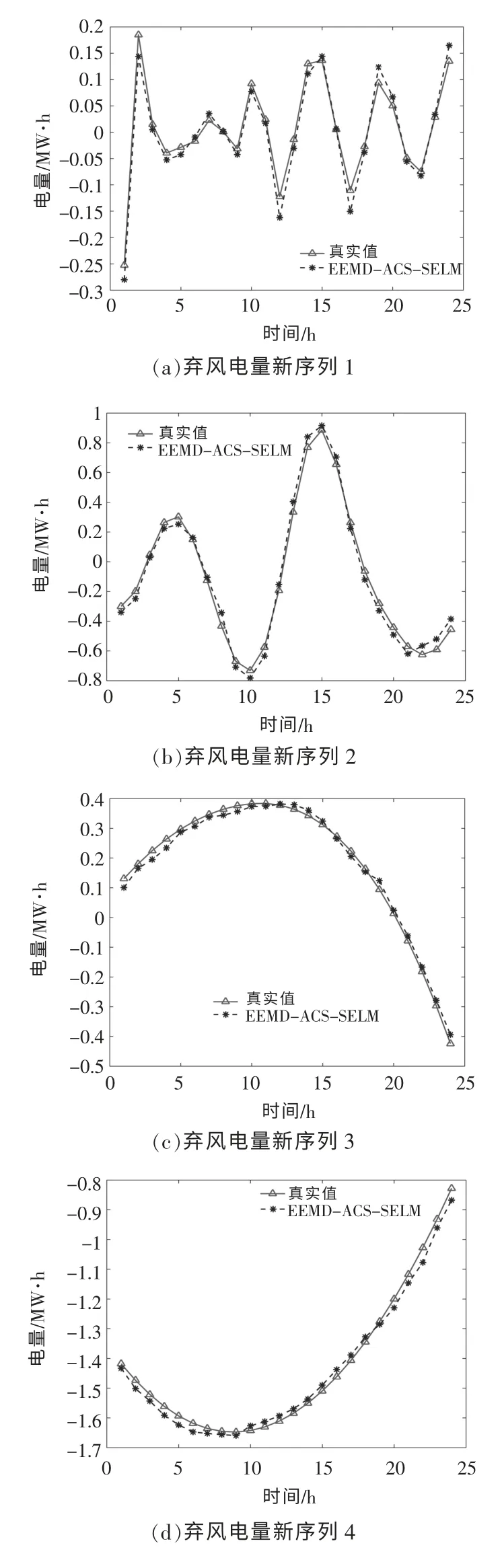
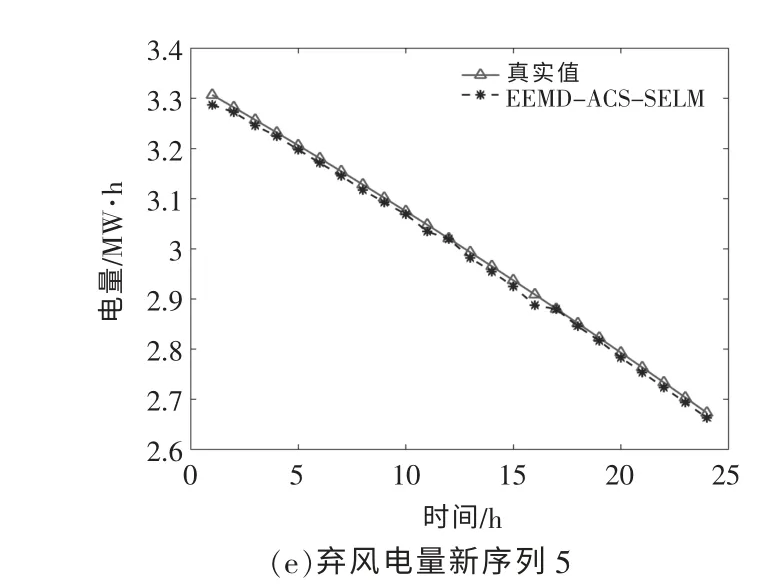
图8 弃风电量新序列的真实值与预测值Fig.8 True and predicted values of the new sequence of wind power curtailment

3.4 各模型预测结果分析

为验证EEMD-ACS-SELM 模型的预测性能，将BP，EEMD-PSO-SELM，EEMD-CS-SELM 和EEMD-ACS-ELM 预测模型作为参照模型。

在EEMD-PSO-SELM 算法中，PSO 算法的种群规模和最大迭代次数与本文ACS 算法设置相同，c1=c2=2.0，ωmax，ωmin分别为0.9，0.4。各模型预测结果为运行20 次的均值，各模型预测结果如图9 所示。

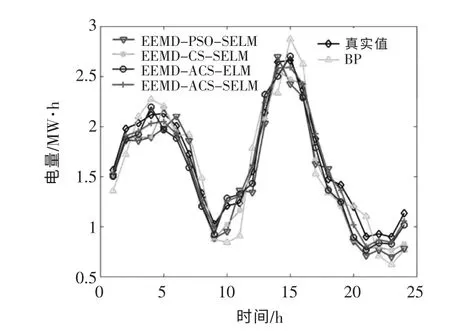
图9 各模型弃风电量预测值与真实值对比Fig.9 Comparison of predicted and true values of wind power curtailment in each model

为对比分析5 个模型的性能，本文选择均方根误差（RMSE）和平均绝对百分比误差（MAPE）作为评判指标，预测性能结果如表2 所示。

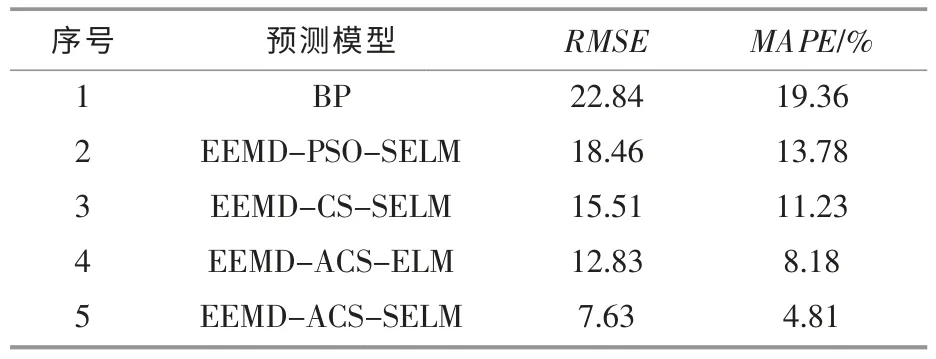
表2 不同预测方法性能比较Table 2 Comparison of performance of different prediction methods

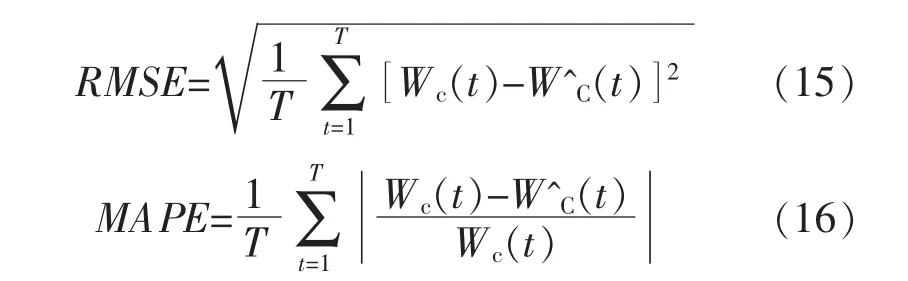
式中：Wc（t），W^C（t）分别为t 时刻风电场弃风电量的实际值和预测值；T 为预测时间点个数。

由图9 和表2 可知：EEMD-ACS-SELM 模型的拟合程度最好，其RMSE 和MAPE 分别为7.63和4.81%，均小于4 种对比实验模型的值，预测结果更加准确；模型5 与模型4 相比，前者对弃风电量的跟随性更好，证明Softplus 激活函数对提高预测精度具有明显作用；模型5 与模型3 相比，前者预测效果更好，是因为t 算子结合CS 算法相比传统的CS 算法，对参数的优化效果更好；模型5的误差指标明显低于模型2 和模型1 的误差指标，表明ACS 算法比PSO 算法具有更强的寻优能力，且组合算法的预测结果要优于单一传统的BP神经网络算法。

综上所述，本文提出的预测方法能够提高弃风电量的预测精度，可为风电场弃风的合理利用提供支持。