基于声学扩散方程的室内声学有限元模拟

杨玉琦，王红卫，於 秀

(华南理工大学 建筑学院，广东 广州 510640)

室内声学是建筑声学的一个分支，研究封闭环境中的声场。室内声学的舒适性影响着人们的心理和生理健康。室内噪声传播的主要途径就是门、窗等耦合开口。耦合空间指相互作用而彼此影响的空间。这两个空间以较小的耦合开口连接在一起，实质上是分离的房间。人们已研究出许多不同的方法来分析耦合空间室内声场，如几何声学、波动声学、统计声学及统计能量分析方法。利用几何声学的声线跟踪法及虚声源法，使室内声场模拟的商业软件ODEON、CATT等应运而生。然而，在进行耦合空间的模拟时，其不能全面描绘出声音的波动特性，且计算时间较长。波动声学理论研究耦合声学以模态分解为基础，模态频率仅限于低频范围。统计声学模型在扩散声场假设下每个房间只产生一个单一值。国内对耦合空间的相关研究均着眼于通过耦合空间达到可调厅堂混响音质的要求，主要的模拟方法为ODEON仿真[1-3]，而对其他室内耦合空间的研究较少。住宅声环境是人们生活质量的重要保证，对其研究主要集中于室外噪声，随着人们对生活品质要求的提高及合租公寓需求的增大，住宅室内噪声的研究显得愈发重要。

室内声学扩散方程模型是基于声能以类似于传热学中粒子的方式传播而应用于室内声学的方法。它可用于预测任意形状房间的声场和吸声材料非均匀分布时的声吸收特性。Valeau[4]等人首先将扩散方程用于耦合空间的研究，Billon[5-6]提出了一种扩散模型来解释通过单墙耦合时声音在源房间和相邻房间之间的传播。Xiang[7]等人提出了修正的Eyring吸收模型，扩展了扩散方程使用的条件，使其适用于高吸收室的预测。并通过有限元模拟及实测数据验证了这一模型。最近，Xiang[8-9]还将扩散方程运用于纪念性教堂空间及地铁车站，均与实测结果呈现出良好的一致性。

本文介绍了扩散方程模型理论的控制方程及边界条件，采用有限元软件comsol中的声学扩散方程接口进行数值模拟。建立了一典型公寓的模型，并对公寓在两种工况下的耦合进行模拟及对比分析——在开门情况下通过门洞耦合，关门情况下考虑门的传输损耗时的耦合。分析其混响时间、室内声压级分布。

1 扩散方程模型理论

1.1 控制方程

本节给出了声学扩散方程的控制方程。室内声学中声学扩散方程是基于声粒子概念，假设粒子在室内空间以声速沿直线运动，在房间边界上发生多次漫反射，并假设能量的反射一定大于吸收，且声能密度和能量流矢量的变化足够小。在这种情况下，根据菲克定律，房间内给定位置r和时刻t处的声能流向量J(r,t)与声能密度w(r,t)的梯度有关。

J(r,t)=-Dgradw(r,t)

(1)

其中V是房间的体积，S是房间的总表面积。

在声能密度随时间变化的区域(V)内存在全向声源q(r,t)时，并将空气耗散作为能量损失。

(2)

其中c为声速，m为空气吸收系数。在式(2)中，对于没有源的任何子域，声源项q(r,t)为零。

1.2 边界条件

使用扩散方程时常用的两种边界条件分别为：一种均匀的边界条件，其中声能不能从房间边界逃脱；及一种混合边界条件，允许声能与边界进行能量交换。可得出混合边界条件下的声学扩散方程模型方程组：

(3)

(4)

其中AX为吸收因子，如果房间墙壁是由N个吸收系数为αi的表面构成,Ax可以写成：

(5)

其中α是具体的表面的吸收系数。AS的下标S表示Sabine吸收。该边界条件下的扩散方程模型仅适用于平均吸声系数低于0.2的低吸收室。为提高与特定房间表面高吸收相关的混合边界条件的准确性，将吸收因子中的Sabine吸收系数替换为Eyring吸收系数：

(6)

1.3 不同应用下的扩散方程模型

1.3.1 通过开口耦合的房间

将一个大空间分为许多个小空间，各个小空间间通过耦合开口来进行耦合，并给不同的子空间定义不同的扩散系数。则在第i个空间中的声学扩散方程如下式所示。

(7)

1.3.2 通过隔墙或门耦合的房间

扩散方程能够模拟当主室发声时，声能量通过带传输损耗的隔墙或门后，临室的声能空间分布，并可拓展到任意数量的耦合房间。与商业的声线跟踪软件，如Odeon比较，可得到相似的结果。然而，Odeon的局限性[10]在于不能应用于低传输损耗(0-10dB)的模拟。下式表示了声音的这种传播。

(8)

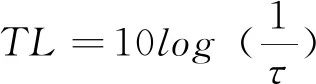
2 仿真模型设置

本文采用多物理场有限元分析软件Comsol Multiphysics中的声学扩散方程接口进行数值模拟。其声学扩散方程接口可用来确定耦合空间的声压级分布以及不同位置的混响时间，并采用有限元方法进行连续空间的离散化。在comsol中，网格尺寸的大小不依赖于波长，而依赖于平均自由程。

根据公寓房间的户型，在comsol中进行建模，房间平面图如下图1所示。层高均设为3 m，耦合开口为各空间的门。网格单元尺寸最小为0.04 m，最大为0.52 m，共建立了5 7064个网格单元。公寓的体积为204.74 m3，表面积为368.94 m2，平均自由程MFP为2.22 m，最大的网格单元尺寸小于平均自由程。由此算得的平均自由时间MFT为0.006 s，Xiang[7]等人的研究表明在至少两到三次MFP后，扩散方程被认为是有效的，所以关于扩散方程求解及结果的分析均在直达声到达后的0.02 s后。声源设置于客厅，坐标为(2.5，4.7，1.2)。选择两种工况来进行计算，通过门洞开口耦合时及当给门一个10 dB的传输损耗时。

模拟中，定义各个表面的各频带吸声系数如下表1所示。经计算可得，房间在500 Hz频带上的平均吸声系数为0.1，仅有部分软包表面吸声系数较大，满足声学扩散方程的使用条件。

表1 各表面吸声系数表

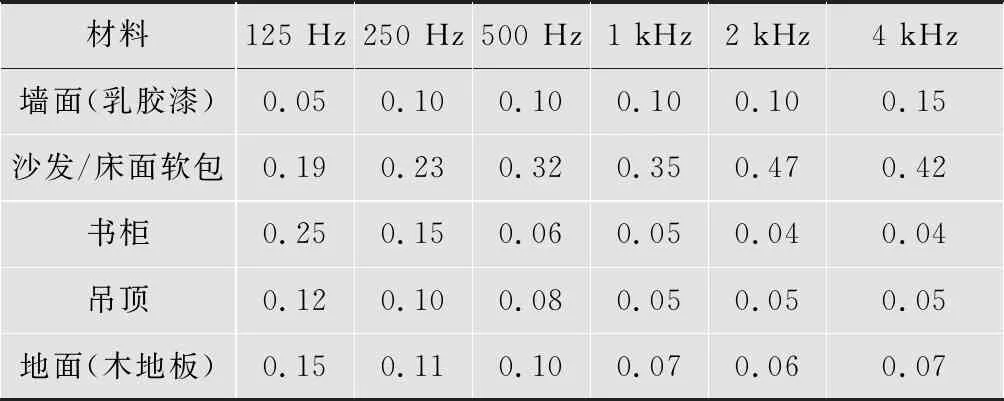
材料125 Hz250 Hz500 Hz1 kHz2 kHz4 kHz墙面(乳胶漆)0.050.100.100.100.100.15沙发/床面软包0.190.230.320.350.470.42书柜0.250.150.060.050.040.04吊顶0.120.100.080.050.050.05地面(木地板)0.150.110.100.070.060.07

3 计算结果及分析

通过求解声学扩散方程，得到空间声能分布水平及声能流矢量的含时解，时间步长取为0.01 s，为避免数据重复，选取关键时间声能流方向变化如下图2所示，t=0.02 s后，开始得到有效的扩散方程解，声能流从位于客厅的声源处，流向各个房间；当t=0.15 s时，主卧的声能流方向发生改变，这表示声能开始从主卧流向外部空间。在其后的时间中，声能流均保持这一方向。

结合如图3所示的混响时间表，当不耦合时，即算得的为每个房间的自然混响时间时，主卧的混响时间大于客厅，这也是声能流矢量改变方向的原因。由于房间耦合的作用，各房间的混响时间得到调节，表现为主卧的混响时间变大，客厅及次卧的相对变小。

这种变化也能在空间声能分布水平图中看到。如下图4所示，在声音刚开始进行传播时，由于平面形式的原因，从客厅传递到主卧的声能量较少，主卧较客卧声压级较小。但由于主卧的声能流方向的变化，使得主卧的声压级逐渐超过次卧。这表明空间的声能分布不仅与声源及接收点的位置有关，也与房间的混响时间及吸声系数有关。在设计住宅平面时不仅应避开直达声，也应通过吸声措施来控制不同功能的房间之间的耦合关系。当给门一个10 dB的传输损耗时，整体的声压级都得到了降低。

4 结语

本文通过详细介绍声学扩散方程模型及在室内不同工况下的应用模型，以一典型公寓模型为例，基于室内声学有限元模拟，探究其室内各空间耦合或不耦合时的空间声能分布及混响时间变化，定性分析了室内平面形式及隔声门对公寓空间声环境的影响，这对利用空间声能分布来研究室内流场分析具有重要意义，可将其利用于现有室内空间的改造及不同室内空间形式的设计，更可将其拓展应用于其他典型耦合空间，如可变混响厅堂，中庭空间，及开放式办公室等。