翼伞系统5段归航轨迹优化研究

高峰, 郭锐, 丰志伟, 揭锦亮, 张青斌

(1.国防科技大学 空天科学学院， 湖南 长沙 410073; 2. 96796部队， 宁夏 银川 750001)

0 引言

翼伞空投系统在军事以及民用上都具有很大的应用价值，可用于跳伞救生、灾区物资投放定点着陆、航天器回收精确归航等。作为近年来空投的新型工具，翼伞折叠体积小、质量轻，并且具有优良的滑翔性能和稳定性。结合导航、制导与控制技术，翼伞系统可在一定初始位置偏差和风场等干扰条件下实现定点无损着陆。

翼伞系统的工作过程主要有拉直、充气、归航控制和雀降，归航方法主要有分段归航法、锥形可行域控制方法和最优控制归航法[1]，在归航过程中施加控制操作改变翼伞飞行方向，以保证雀降着陆的精确性和稳定性。翼伞空投着陆点环境复杂，着陆范围广，着陆的不确定性大，归航方法对着陆的成功与否影响较大。针对该问题，Li等[2]对翼伞归航轨迹进行分段处理，采用定线目标寻的方法有效解决了着陆点范围问题。滕海山等[3]针对运载火箭助推器一子级无控坠落地面落点散布较大的情况，提出了一种翼伞系统的线目标归航方法。Gao等[4]采用分段归航方法设计了翼伞归航轨迹，并利用基于种群的量子差分进化算法对轨迹优化。Sun等[5]设计了飞行复合寻的法，先对翼伞空轨迹采用经典径向归航方法分段，再考虑风场作用，对轨迹跟踪控制。蒲志刚等[6]提出了翼伞分段归航控制的方向控制方法，探讨了位置控制和方向控制在归航过程中的优先权问题。胡文治等[7]以耗能最少和落地误差最小为优化目标，对翼伞采用左侧下拉和右侧下拉耗能情况进行了比较。Suresh Babu等[8]以耗能最小和落地点误差最小为目标，利用直接多次射击法求得最优路径。Yang等[9]采用遗传算法求解了翼伞分段归航的最优轨迹，并以贝塞尔曲线为基础对翼伞末制导进行路径规划，以处理变滑翔比的情况。Zou等[10]针对翼伞精确空投问题，为提高翼伞轨迹跟踪控制精度，提出一种区间型模糊逻辑自整定参数方法，并通过试验验证了方法的有效性和实用性。分段归航使得实际控制量函数变得简单，利于工程实现。经典的分段归航一般分为向心飞行段、能量保持段和着陆段[11]。周靓[12]根据归航任务需求不同，进一步细分为5段归航法，在3段归航基础上增加了初始准备阶段和方向调整阶段，使得归航轨迹更加接近真实情况。

尽管翼伞系统具有成本低、易于工程实现的优点，但其也具有可控能力弱、受环境因素影响大的缺点。因此寻求适合于工程实现的归航策略一直是翼伞系统的关键技术。为解决翼伞系统的实时归航问题， 本文采用拟坐标法建立翼伞系统高保真度的两体9自由度动力学模型，并通过空投试验验证模型的有效性；在此动力学模型基础上，利用数值实验结果获得翼伞系统稳态飞行特性，给出了翼伞系统飞行的滑翔比和转弯速率限值，得到了近似4自由度模型；采用5段归航策略，以第1、第5阶段飞行时间和第2、第4阶段偏航角速度为优化参数，以5段归航轨迹为初始条件，以偏航角加速度不超过极限值为过程约束条件，以归航耗能最少为优化目标，利用伪谱法给出了翼伞最优归航方案；对直接归航和5段归航两种方法的耗能情况以及控制量函数的难易实现程度做了比较，为空投过程提供理论参考。

1 翼伞系统建模

本文研究对象为某型弹载荷翼伞系统，结构如图1所示。翼伞系统主要分为伞衣、伞绳、吊带以及载荷4部分。将伞衣、伞绳整体记为刚体A，将吊带、载荷整体记为刚体B. 刚体A具有3个平动自由度和3个转动自由度，刚体B通过球铰和刚体A连接，系统共计9个自由度。为得到翼伞系统飞行过程的稳定速度、滑翔比、转弯半径等特征参数，本文首先建立较精确的9自由度模型。

1.1 坐标系定义

如图2所示，将发射坐标系(惯性系)记为OIxIyIzI，伞衣坐标系记为OPxPyPzP，刚体A体坐标系记为OAxAyAzA，载荷坐标系记为OSxSySzS，刚体B体坐标系记为OBxByBzB，刚体A和刚体B连接处为铰点O，速度坐标系记为OVxVyVzV.

图2 翼伞系统坐标系示意图Fig.2 Schematic diagram of coordinate system of parafoil

记φ、θ和ψ分别为刚体A在惯性系下的滚转角、俯仰角和偏航角，p、q、r为对应在惯性系下的角速度；φr、θr和ψr分别为刚体B体坐标系相对刚体A在惯性系下的滚转角、俯仰角和偏航角，pr、qr、rr为对应的相对角速度；α、β分别为翼伞攻角和侧滑角；ΓP为伞衣安装角，ΓS为载荷安装角。则从惯性系到刚体A体坐标系转换矩阵为EAI(φ,θ,ψ)；从刚体A体坐标系到刚体B体坐标系转换矩阵为EBA(φr、θr、ψr)；从刚体A体坐标系到伞衣坐标系转换矩阵为EPA(ΓP)；从刚体B体坐标系到载荷坐标系转换矩阵ESB(ΓS)；从伞衣坐标系到速度坐标系转换矩阵EVP(β,-α)。为便于分析，本文假设伞衣安装角ΓP和载荷安装角ΓS均为0°，则EPA=ESB=I，其中I为3阶单位矩阵。

1.2 9自由度多体动力学建模

翼伞在飞行过程中受力主要包括自身重力G、气动力Fa以及发动机推力Ft. 图2所示刚体A、刚体B两体模型中，系统所受合外力在刚体A体坐标系下表示为

(1)

式中：GA、GB分别为刚体A、刚体B所受的重力；FaA、FaB分别为刚体A、刚体B受到的气动力；FPM为伞衣的附加质量对伞衣质心的作用力；Ft为作用于载荷的螺旋桨推力。

伞衣气动力系数CL、CD、CY和力矩系数Cl、Cm、Cn采用多项式模型描述，即

(2)

(3)

式中：δs为对称舵偏；δa为反对称舵偏；vPV为伞衣质心相对气流的速度；b、c为伞衣展长和弦长，其他参数k、CL0、CLα、CLδS、CLδa、CD0、CDδS、CDδa、CYβ、CYp、CYr、CYδa、Clβ、Clp、Clr、Clδa、Cm0、Cmα、Cmq、CmδS、Cmδa、Cnβ、Cnp、Cnr、Cnδa均为气动力常系数。

作用在伞衣质心的气动力为

(4)

式中：S为伞衣参考面积。

刚体A所受合力矩在其体坐标系下表示为

(5)

式中：rAM为在刚体A体坐标系下刚体A的质心到铰接点之间的矢径；rMB为在刚体B体坐标系下铰接点到刚体B质心的矢径；rBS为在刚体B体坐标系下刚体B质心到载荷质心矢径；MaA、MPM分别为刚体A受到的气动力矩、伞衣附加质量在刚体A质心处产生的力矩。气动力矩表示形式为

(6)

式中：ρ为空气密度。

刚体B所受合力矩在其体坐标系下表示为

(7)

载荷气动力形式为

(8)

式中：v为载荷质心速度；Sd为载荷参考面积；Cd为载荷阻力系数。

为便于分析建模，选取翼伞系统两体模型的拟坐标为

(9)

式中：RA、θA、θBA分别为刚体A在惯性系下的质心位移、姿态角以及刚体B相对于刚体A的姿态角，具体形式为

(10)

相应的，选取拟速度为

(11)

式中：vA为刚体A在其体坐标系下的质心速度，ωA为刚体A在其体坐标系下的角速度，ωBA为刚体B相对于刚体A的角速度，具体形式为

(12)

则翼伞系统拟坐标形式拉格朗日动力学方程为

(13)

式中：L为拉格朗日函数，对拟速度ω偏导为

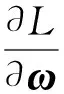
(14)

(15)

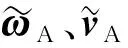
(16)

C为惯性系到刚体A体坐标系的坐标转换矩阵，DA、DBA分别为刚体A和刚体B的欧拉角时间导数到其体角速度的坐标转换矩阵；广义力矩阵Q*表示为

(17)

系统的运动学方程为

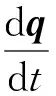
(18)

建立9自由度动力学模型的目的是为了开展精确的仿真，以便确定更接近于实际情况的翼伞稳定飞行水平速度、稳定滑翔比以及偏航角速度限值等参数。为保证建立模型的准确性，对系统进行空投试验，选择试验的当天天气状况良好。空投环境风场在发射坐标系下水平方向分解为xI轴和yI轴两个方向，分别记为wxI=-0.5 m/s，wyI=0.25 m/s. 绘制试验与仿真的轨迹坐标随时间变化曲线，如图3所示。

图3 试验与仿真坐标位置随时间变化曲线比较Fig.3 Experimental and simulaed position coordinates over time

试验与仿真的xI轴、yI轴、zI轴方向坐标随时间变化曲线趋势一致，在xI轴和yI轴方向曲线偏差一部分是仿真风场与实际风场差别引起，一部分是所建立模型与真实模型的差异导致。3条飞行曲线与仿真曲线总体趋势一致说明了该模型参数的有效性。

利用上述翼伞参数，采用表1数据作为初始条件，对9自由度翼伞系统仿真，得到轨迹三维曲线如图4所示，得到偏航角速度随时间变化如图5所示。考虑到实际情况，翼伞下拉偏量须有一定余量，故本文取翼伞转弯过程下拉偏量最大为总偏量的60%.

表1 9自由度模型仿真初始条件

图4 翼伞9自由度系统模型仿真三维轨迹Fig.4 3-dimensional trajectory of 9-degree-of-freedom parafoil system model simulation

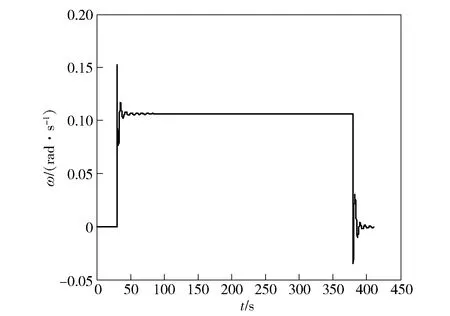
图5 60%下拉偏量下偏航角速度随时间变化曲线Fig.5 Variation curve of yaw angle velocity with time under 60% pull-down deviation

翼伞在t为30～380 s时段转弯，对称舵偏为0，反对称舵偏取最大60%，由图4可知翼伞系统的最小转弯半径Rmin=55 m，由图5可知稳定飞行时的最大偏航角速度ωmax=0.106 2 rad/s. 仿真得到稳定飞行水平速度大小为5.894 m/s，稳态滑翔比为2.3.

1.3 4自由度质点模型

为便于工程中进行实时归航设计，需要将翼伞系统简化为4自由度质点动力学模型[8,14-15]，该模型包括3个平动自由度和1个转动自由度，如(19)式所示：

(19)

式中：vh为翼伞飞行水平速度大小，vh=5.894 m/s；ψs等价于偏航角；ω等价于偏航角速度大小，-ωmax≤ω≤ωmax；u等价于(偏航角加速度)控制量，-umax≤u≤umax，umax为偏航最大角加速度，由控制系统电机驱动，umax=0.1 rad/s2；垂直速度vzI与水平速度vh满足

(20)

LD为滑翔比，LD=2.3.

控制量u和转弯半径R以及飞行水平速度vh之间满足关系式：

(21)

2 伪谱法轨迹优化

2.1 5段归航法简介

为了能够进行实时归航计算，本文采用基于4自由度质点动力学模型的翼伞系统分段归航策略，该方法所需要考虑的参数较少，且每一段轨迹对应的控制量为常数。如图6所示为5段归航示意图，已知初始点OI(xIOI,yIOI,zIOI)，初始偏航角大小ψ1，水平速度大小vh，竖直速度大小vzI，目标点F(xIF,yIF,zIF)，着陆偏航角大小为ψF.

在第1阶段，翼伞从归航轨迹的起始点O滑翔飞行到盘旋区域上空P点，该过程对翼伞不施加控制；在第2阶段，翼伞消耗多余的高度，从P点开始盘旋下降直到高度适中再从C点飞出盘旋区，该过程对翼伞施加单侧下拉控制；在第3阶段，翼伞从盘旋区C点飞出，经过一段时间滑翔，到达目标点附近区域D点，该过程对翼伞不施加控制；在第4阶段，外部风场干扰使得翼伞飞行方向偏离目标点，需要进行180°转弯以校正方向，之后到达E点，进入最终的逆风雀降段，该过程对翼伞施加单侧下拉控制；在第5阶段，翼伞逆风雀降着陆，该过程对翼伞施加双侧下拉控制。在本文中，对翼伞在转弯过程的控制，只采用单一的左侧下拉方式。相比于左右两侧交替下拉，单侧下拉方法对能量的损耗较小，同时也可以降低翼伞系统的不稳定性[16]。

2.2 5段归航解析解

如果不考虑最优轨迹优化问题，给定转弯半径，就可以获得5段归航法的解析解。由于归航过程zI轴方向速度为常数，因此zI坐标可由时间t唯一确定，故而此处不作求解，进而可仅对二维平面轨迹求解，如图6所示， 从2.1节5段归航介绍知，第2阶段和第4阶段转弯，设转弯半径分别为R2、R4，第1、第3、第5阶段为直飞。设第i阶段飞行时间为Δti，i=1,2,3,4,5. 根据归航轨迹特性，只需要确定第1段飞行时间Δt1、第5段飞行时间Δt5、R2和R4，整条轨迹即可解析求解得到。图6中，vw为风速，由几何关系得ψ′2=ψ3=ψ4，ψ1=ψ2.

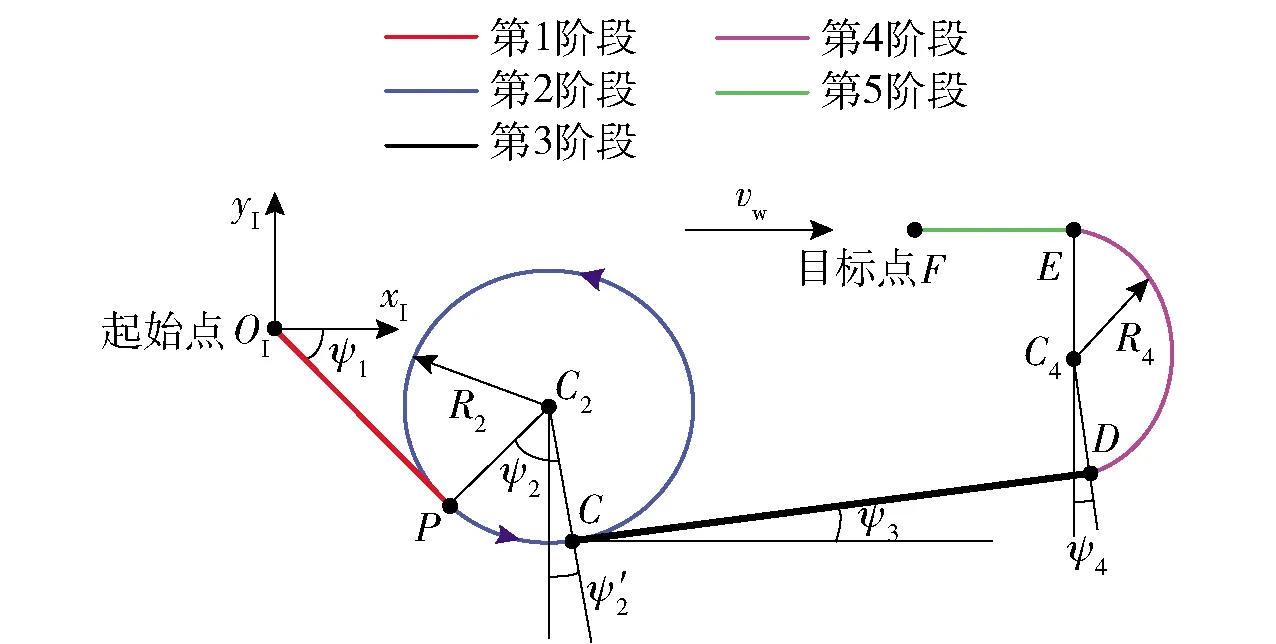
图6 翼伞系统5段归航示意图Fig.6 Schematic diagram of five segments homing of parafoil system

求解归航过程特征点P、C、D、E、C2、C4以及特征角度ψ2、ψ′2、ψ3、ψ4如下：

特征点P坐标为

(22)

特征点C2点坐标为

(23)

特征点E坐标为

(24)

特征点C4点坐标为

(25)

特征点C坐标表示为

(26)

特征点D坐标表示为

(27)

向量CD与xI轴正方向的夹角为

(28)

第2阶段盘旋圈数n可由(29)式确定：

(29)

给出整个归航轨迹的初始点和终点的坐标及偏航角、水平速度以及滑翔比，第1、第5阶段的飞行时间，如表2所示，其中Rmin=55 m. 从初始点开始经过Δt1=20 s后开始单侧下拉以调整前进方向和消耗高度，同时为保证雀降能顺利实施，要求最终雀降时间Δt5不小于10 s.

表2 初始条件

由表2所给条件，结合图6，依据(22)式～(28)式，转弯半径取R2=R4=100 m，所有角度大小限制在0～180°，求解得到5段归航轨迹的特征点及特征角度如表3所示。

需要说明的是，上述计算中没有考虑能量消耗情况，并非最优解。下文将在考虑耗能最小情况下对轨迹进行优化求解。

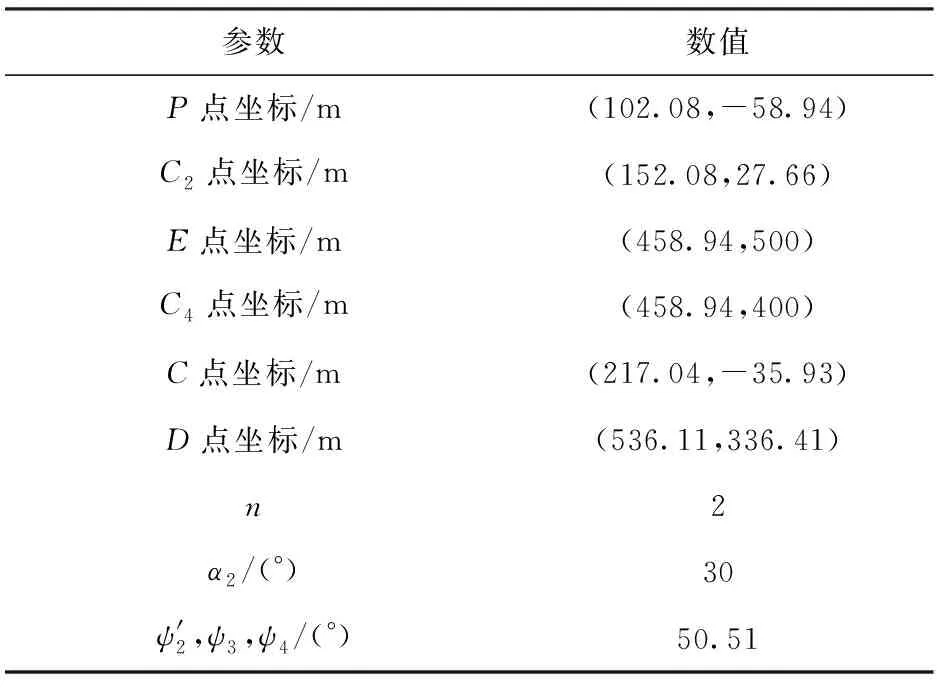
表3 轨迹解析解

2.3 轨迹最优化求解

高斯伪谱法将状态量(xI,yI,zI,ψ,ω)和控制量u进行离散，然后在离散点上构造拉格朗日插值多项式，采用适当的非线性规划得到最优解，在处理含初始和终端约束的问题上具有较大优势[17-18]。

采用高斯伪谱法进行轨迹优化，设定优化目标为耗能最小，即

(30)

式中：t0和tf分别为优化的初始和结束时间点。

设控制约束为

(31)

5段归航代数约束方程如(19)式～(21)式。

为了降低伪谱法中非线性规划的迭代次数，提高计算效率，将表3中的轨迹特征数据作为伪谱法优化的初始解。此外，将5段归航法和直接归航法进行对比。直接归航法以起始点坐标和偏航角为初始条件，以落地目标点坐标和偏航角为终端约束，同样以偏航角速度、角加速度不超过最大值为过程约束，通过优化得到一条满足条件的参考轨迹。相比于分段归航法，直接归航法不考虑中间过程，只要轨迹满足约束条件即可。

仿真得到优化后的轨迹三维曲线如图7所示。在5段归航模式下，翼伞第1阶段飞行20 s下降到948.7 m开始盘旋下降，经过255.6 s盘旋两圈下降到293.80 m的高度，之后朝着目标点飞行64.60 s到达方向修正起始点D，再经过39.8 s完成方向修正，然后逆风向目标点飞行，再经过10 s后雀降着陆到达目标点F. 在直接归航模式下，翼伞从初始点开始经过一系列转弯过程到达目标点。三维轨迹地面投影如图8所示，翼伞最终着陆方向沿着风场反方向。考虑实际偏航角速度不能突变，本文设其按照一定速率线性增大或减小，如图9和图10所示。第2阶段偏航角速度从0 rad/s开始以0.006 rad/s2的加速度增大到0.060 46 rad/s后稳定，此时转弯半径为97.5 m，而后又以-0.001 7 rad/s2的加速度减小到0 rad/s；第4阶段先以0.006 5 rad/s2的加速度增加到0.077 63 rad/s稳定，此时转弯半径为76 m，而后以-0.006 4 rad/s2的加速度减小到0 rad/s. 整个过程中偏航角速度连续线性变化，偏航角加速度通过电机操控在一定小范围内可突变，在工程上切实可行。

图7 归航三维轨迹曲线Fig.7 Homing 3D trajectory curves

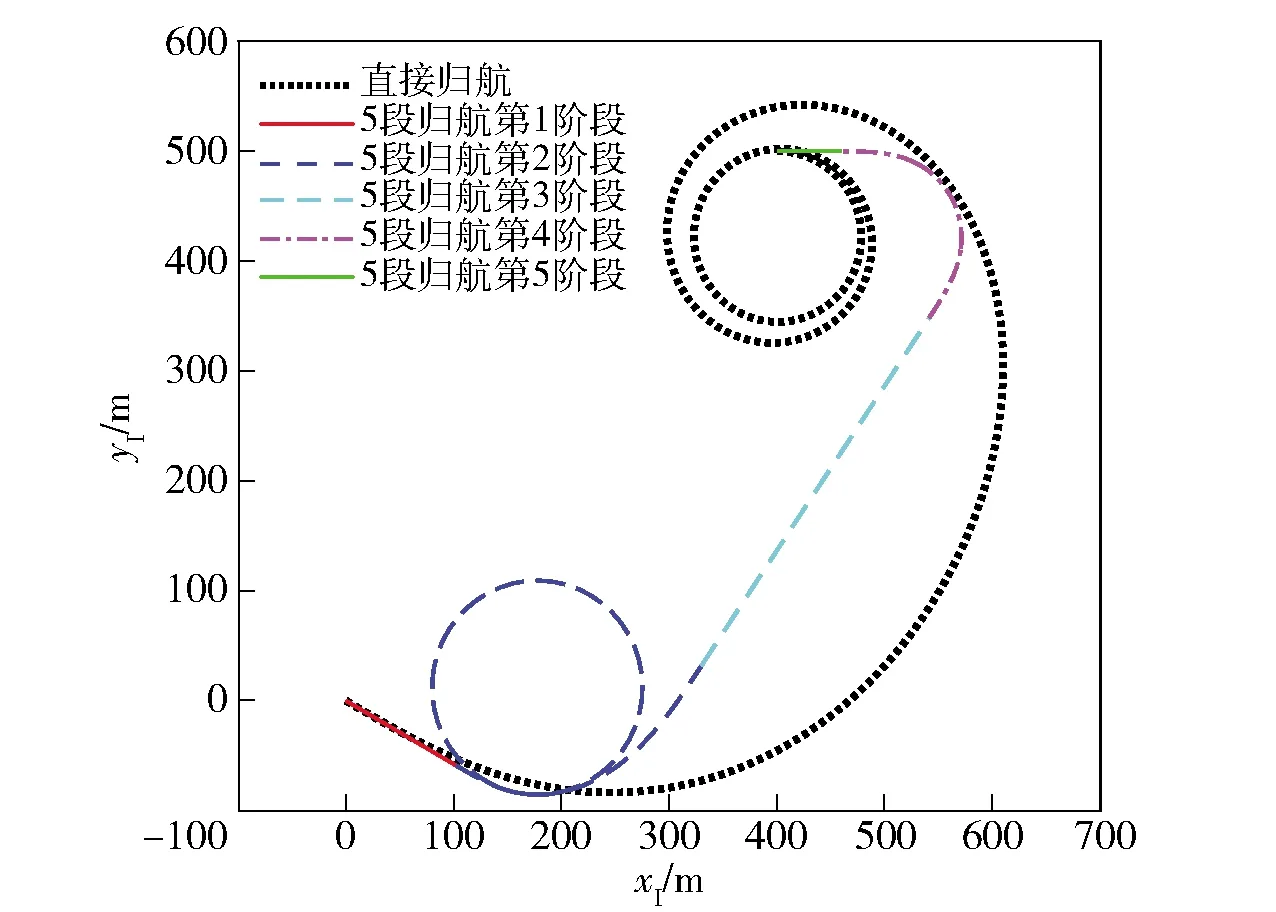
图8 归航轨迹在水平面投影Fig.8 Homing trajectory projected on the horizontal plane

图9 角速度随时间变化曲线Fig.9 Changing curves of angular speed with time

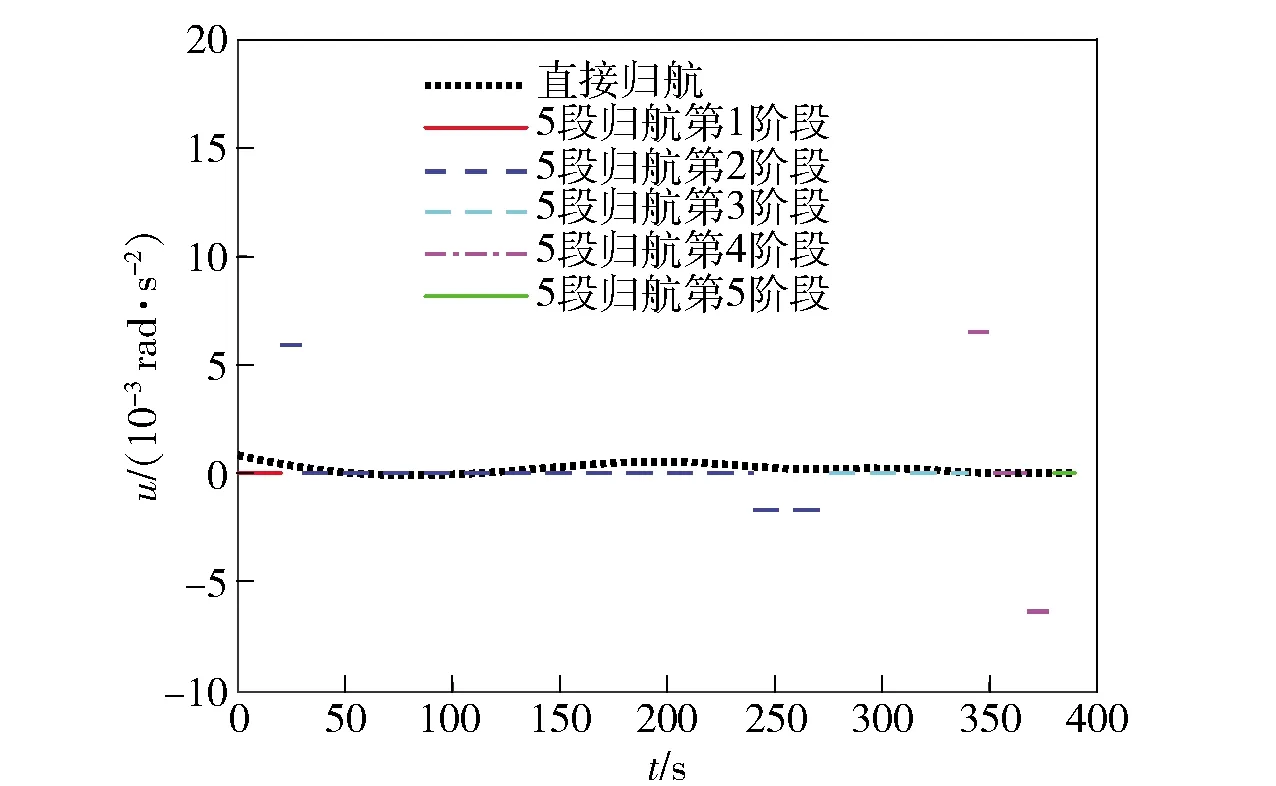
图10 控制量随时间变化曲线Fig.10 Changing curves of control quantity with time

将5段归航轨迹作为伪谱法优化的初始解，利用MATLAB软件运算耗时约4.5 s左右，而仅给出初始点和目标点然后进行5段优化，伪谱法需要在很大范围内寻找最优解，耗时约在30 s附近，且耗时、能否得到最优解均与设定范围大小有关。因此，对翼伞系统分段归航而言，预先求解轨迹的特征点，可在一定程度上较大地提高运算效率。

直接归航法和给出特征点的5段归航法两种方法在优化过程中耗能如表4所示。以偏航角加速度在时间上的积分为耗能参考，则5段归航法耗能约为直接归航法的50倍。对图9和图10进行比较分析可得：直接归航法过程简单，耗能少，但控制量u随时间变化复杂，实现难度大；5段归航过程总耗能较大，但每段的控制量均为常数，便于实际操控。在实际应用中，可根据翼伞系统能达到的最小控制精度以及耗能要求合理选择归航方案，以求在精度能达到的情况下耗能最少。

表4 两种归航方法耗能比较

3 结论

本文建立了翼伞系统拟坐标形式的两体9自由度动力学模型方程，通过飞行试验验证了模型的有效性；采用数值方法仿真求解了系统滑翔比及最大转弯速率，进而得到翼伞系统简化的4自由度模型特征参数；考虑5段归航方法，并将5段归航轨迹特征点作为伪谱法优化的初始解，以耗能最小为目标求得最优轨迹，最后将直接归航轨迹及耗能情况与之作比较。得出如下主要结论：

1)所建立的9自由度模型真实有效，可作为翼伞系统数值分析的模型参照。

2)翼伞4自由度模型可由复杂高自由度模型适当简化得到。

3)与直接归航法的轨迹优化比较，将5段归航法轨迹的特征点作为伪谱法优化初始解可显著提高计算效率。

4)5段归航伪谱法优化轨迹相比于直接归航方法耗能较多，但其每段的控制量均为常数，在能耗允许条件下5段归航法更具有工程实用价值。