舰炮含钳爪回转机构的伸爪运动特性研究

彭京徽， 王德石， 张弘弨

(1.海军工程大学 兵器工程学院， 湖北 武汉 430033；2.海军研究院， 北京 100161)

0 引言

为满足空间和运转要求，回转运送机构普遍应用于货物运输机械。大口径舰炮转弹机是一种含钳爪回转运送机构，相比于其他货物运输机械，具有承受强冲击、高转速和变负载的特点[1]，研究回转运输机构的运动特性对降低系统故障率，提高供弹机构动作可靠性有着重要意义。国内外学者对间歇式回转运输机构的研究不多[2-4]，主要集中在重型回转机构[5-8]。对含钳爪回转机构伸爪运动而言，其运动与机械手类似，应满足良好的定位要求，文献[9]给出了计算二自由度机械手动力学的一般方法。张大鑫[10]主要从整体结构、动作方案设计和各关节之间的传动关系等方面对多自由度取放机械手的结构设计和运动进行了分析。陈功等[11]利用解析法对6杆组合机构的机械臂进行速度及加速度分析，并优化结构设计。申团辉等[12]利用多体动力学仿真软件ADAMS和数学仿真软件MATLAB/Simulink联合仿真研究一种基于曲柄滑块机构原理设计的简易农用移栽机机械手夹持机构。机器人动力学方程非常复杂，相关的研究方法有拉格朗日方程、牛顿- 欧拉方程[13]、凯恩方程、广义达朗贝尔原理[14]等。其中，牛顿- 欧拉方程和拉格朗日方程是两种较为高效的求解机器人动力学模型方法。对于牛顿- 欧拉方程，在机器人关节速度、角速度已知时，运用牛顿- 欧拉公式求解出各个关节驱动力矩的递推公式，再根据递推公式求解出机器人动力学数学模型。拉格朗日方程是整体系统能量对系统变量及时间的微分而建立的。对于简单系统，使用拉格朗日方程比较繁琐，但是，系统较为复杂时，使用拉格朗日方程求解的效率就会体现出来[15]。上述文献对机械手臂的运动研究主要还是控制与路径规划，鲜有研究机械手手指的运动特性。

因此，本文首先以含钳爪回转运送机构为对象得到机构运动的简化杆件模型，根据伸爪运动过程中的构型变化、多坐标系的转换关系和封闭矢量法进行了机构伸爪的运动学分析；然后，进行机构伸爪受力分析、利用达朗贝尔原理和拉格朗日方程建立了机构伸爪的动力学方程；最后，基于机构的几何参数与驱动参数，通过MATLAB软件进行了算例分析。

1 机构模型与运动分析

含钳爪的回转运送机构主要由转轴、轮盘、钳爪以及其他辅件等组成，其中钳爪主要包括钩爪、驱动杆、偏心销等部件，具体结构如图1所示。

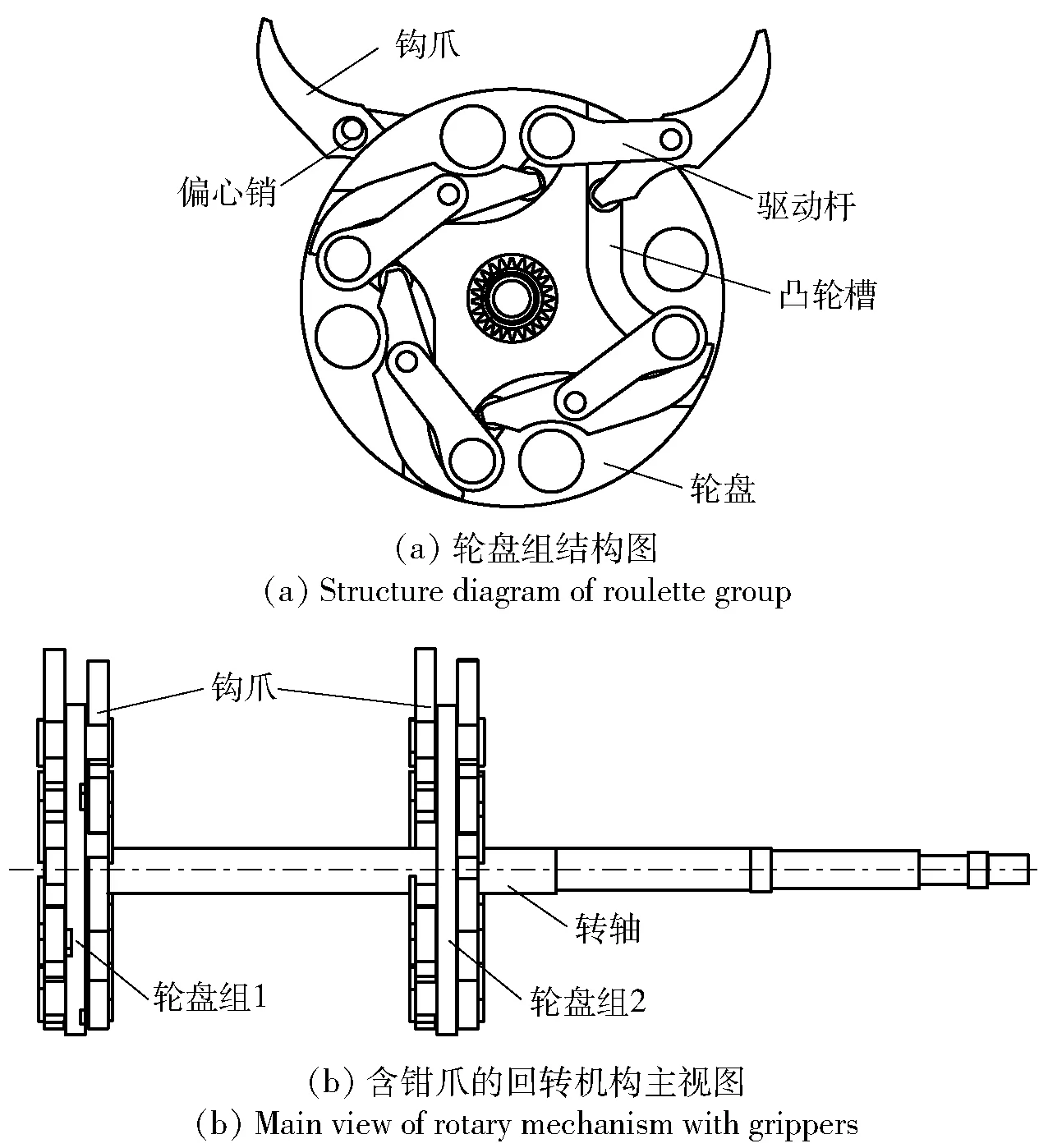
图1 间歇式钳爪回转运送机构Fig.1 Intermittent rotary mechanism with claws

其工作机理是：由两组双钩爪同时进行伸爪，转轴转动作为外部驱动转矩M0促使轮盘转动，转盘上的驱动杆、钩爪等组件随轮盘一起转动；而驱动杆同时受到外部驱动转矩M1和M2驱动，带动钩爪运动，但钩爪下部凸轮受到轮盘上凸轮槽的约束，凸轮沿凸轮槽方向运动，从而逐步进行由规定路径的伸爪运动，直至轮盘转动90°，钩爪在转弹起始位置完成伸爪动作，钩爪夹紧物体。每组双爪的两个爪在伸爪运动时的位置存在对应关系，因此在实际研究时可以先研究一个爪伸爪时的运动特性问题。同时，伸爪运动过程受到两个外部转矩驱动，包括转轴驱动轮盘转动和辅件促使驱动杆带动钩爪运动，进而完成伸爪动作。在运动模型简化中将偏心销视为间隙，先忽略间隙对理论运动轨迹带来的影响，得到的单钩爪和双钩爪运动简化模型分别如图2(a)、图2(b)所示。

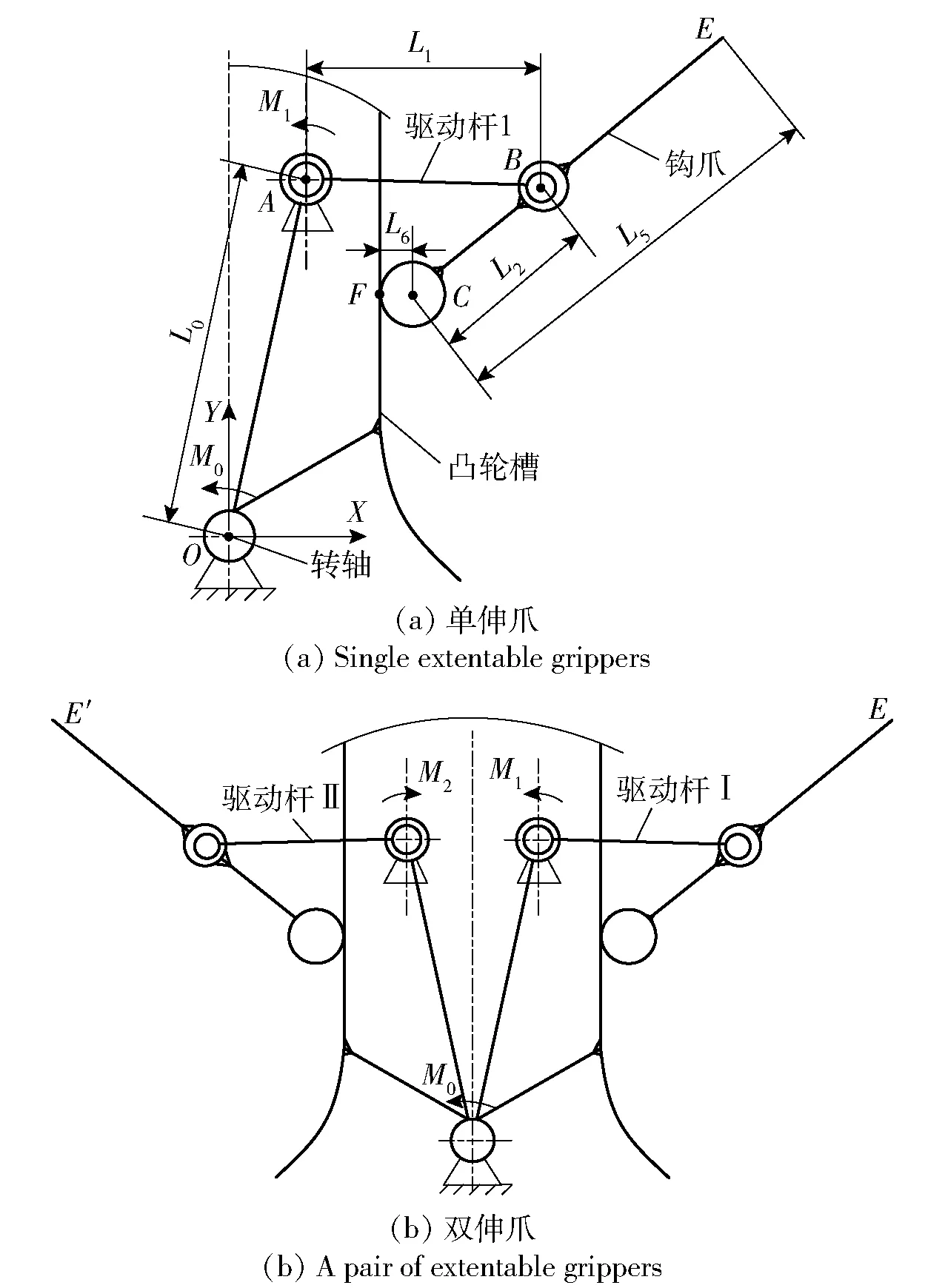
图2 运动简化杆件模型Fig.2 Simplified model of lever motion

图2中：O、A、B、C、E、F分别是转轴中心、驱动杆转动副中心、驱动杆连接孔中心、凸轮中心、钩爪末端位置、凸轮与凸轮槽接触点；L0、L1、L2、L5、L6分别是转轴中心到驱动杆转动副中心的距离OA、驱动杆长度AB、钩爪连接副中心到凸轮中心的距离BC、凸轮中心到钩爪爪尖的距离CE、凸轮半径CF；M0、M1、M2分别是转轴、驱动杆Ⅰ和驱动杆Ⅱ的驱动转矩。

2 机构伸爪过程的运动特性

2.1 伸爪过程的运动约束分析

图3 伸爪运动等效图Fig.3 Equivalent figure of extentable gripper motion

由图2可将伸爪过程等效为图3所示以A点为原点的局部坐标系下运动过程的3个状态。图3中起始状态的AB、BC、CD和DA分别对应Ⅰ杆、Ⅱ杆、Ⅲ杆和Ⅳ杆，分别建立Axy坐标系和Auv坐标系。由图3可将伸爪过程分为两个阶段，分别对应的时间和构型等参量如表1所示，其中Ⅰ杆、Ⅱ杆、Ⅲ杆和Ⅳ杆分别对应长度为L1、L2、L3、L4.

表1 不同时间段对应的参量

在t0～t1时间段，由封闭矢量法可建立Auv坐标系下4杆机构运动方程，A、B、C、D对应坐标分别是(uA，vA)、(uB，vB)、(uC，vC)和(uD，vD)，Ⅰ杆、Ⅱ杆、Ⅲ杆和Ⅳ杆与u轴对应夹角分别记为θ1u、θ2u、θ3u和θ4u，其中uA=0 mm，vA=0 mm，θ4u=0°.

(1)

因此，钩爪末端点E的坐标(uE,vE)为

由表1可知x轴与u轴的夹角α，则任一点Mi(i=1，2，…)在两个坐标系中的坐标分别为(xMi,yMi)、(uMi,vMi)，且用向量q、δ分别表示Axy和Auv坐标，θi和θiu分别为Mi在Axy和Auv坐标系对应的角度，对应几何关系的矩阵形式为

因此，得Axy和Auv坐标的转换矩阵关系式为

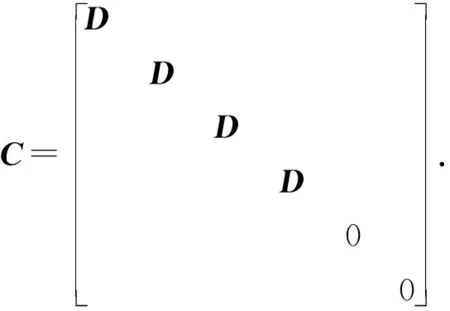
基于上述Axy坐标系与Auv坐标系的转换，在t1～t2时间段，建立Axy坐标系下曲柄滑块机构的运动方程：

(2)

式中：SC为AC的x轴方向的距离；R为y轴方向的距离。解得

在以转轴O原点建立的全坐标系OXY下：(XA,YA)=(L0cosβ,L0sinβ)，(xM,yM)=(-yM,xM)，(XM,YM)=(xM,yM)+(XA,YA)，β是OA杆与X轴的初始夹角，用向量η表示全坐标系下的坐标，B表示转换矩阵。轮盘转角γ=ω0t(ω0为轮盘角速度)，根据转换公式可求得全坐标系下各点对应的坐标：

2.2 伸爪过程的动力学特性

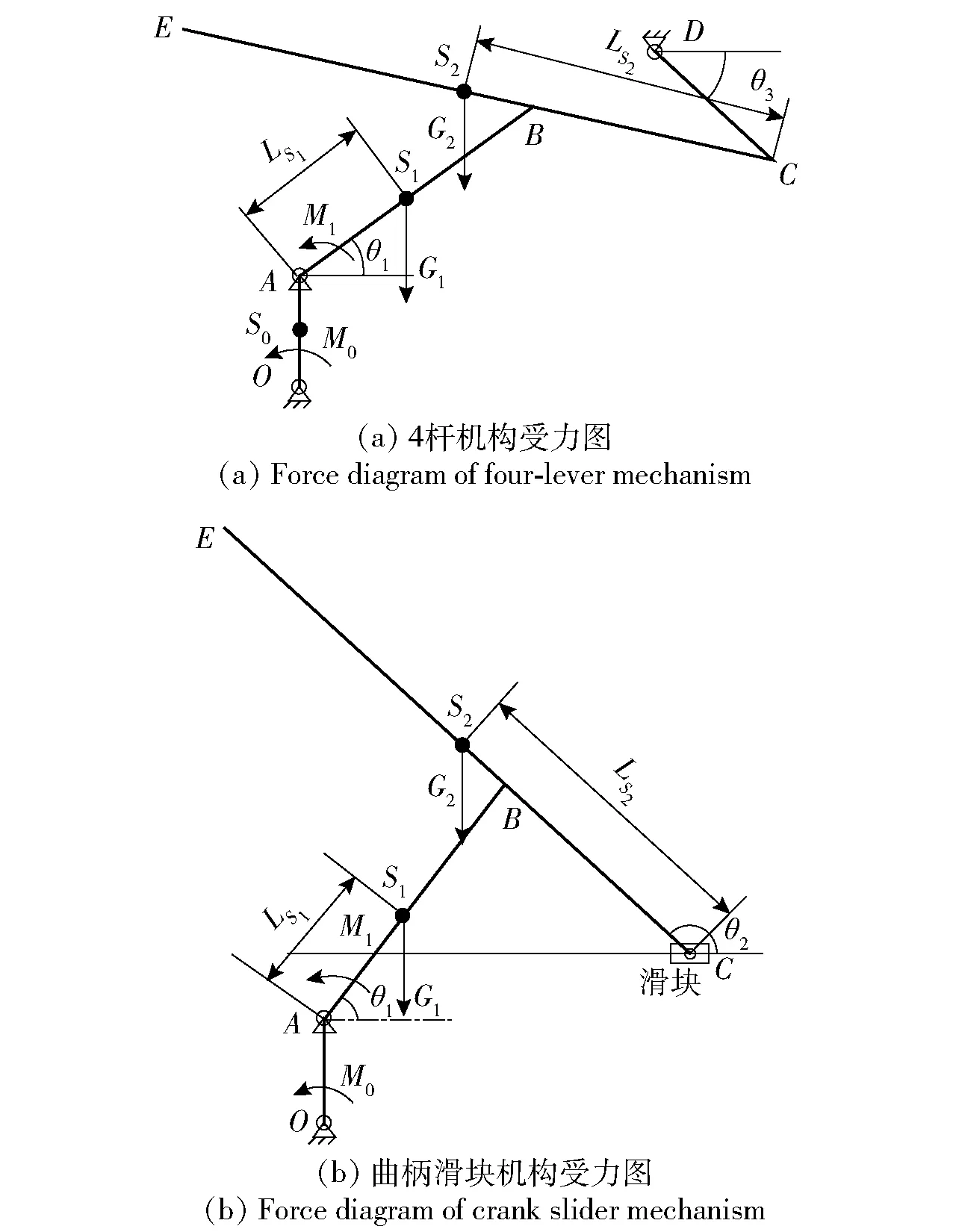
图4 两种构型机构的受力分析Fig.4 Force analysis of two configurations of rotary mechanism

机构在t0～t1时间段，构型为4杆机构；在t1～t2时间段，构型为曲柄滑块机构。两构型分别如图4(a)、图4(b)所示。图4中CD为无质量构件杆Ⅲ，滑块为无质量构件，S0、S1、S2分别表示轮盘组、杆Ⅰ和钩爪的质心，LS1、LS2分别表示A点到S1的距离和C点到S2的距离，OA机构质量集中在A点，LS0是转盘偏心距离，考虑到机构过于复杂且轮盘组质量远大于钩爪质量，假设O点到轮盘组S0的LS0距离保持不变。

拉格朗日方程：

(3)

(4)

δW0=F0δq0+F1δq1，

(5)

(6)

δW0=δW1，

式中：H为系统总动能，

(7)

令

式中：J11、J22、J12均具有转动惯量的量纲，称为2自由度系统的等效转动惯量；G0是轮盘的重力；G1是驱动杆的重力；G2是钩爪的重力；ηSnX和ηSnY分别表示坐标系OXY中Sn点的坐标；LSn是质心Sn到相应点的距离；qSnX和qSnY分别表示坐标系Axy中Sn点的坐标。

由此可计算出质心S1、S2矩阵形式的运动轨迹方程，整理可得伸爪运动的微分方程：

3 算例分析与仿真研究

利用MATLAB软件数值计算和ADAMS软件虚拟样机仿真对伸爪过程的运动特性进行分析，分别取m0=3 kg、m1=0.05 kg、m2=0.10 kg、L0=0.133 69 m、L1=0.095 2 m、L2=0.063 91 m、L3=0.062 m、L4=0.144 07 m、L5=0.191 7 m、R=0.042 6 m、ω0=π/6 rad/s、ω1=5π/54 rad/s、α=40.05π/180 rad、β=76.5π/180 rad、θ10=33.16π/180 rad、θ1u0=13.34π/180 rad进行算例分析。

3.1 运动曲线分析

由上述数据经MATLAB软件数值计算和ADAMS软件样机仿真计算可得E(XE,YE)的运动坐标、E点到全局坐标原点O的距离LOE变化以及OE转角变化，分别如图5(a)、图5(b)和图5(c)所示，其中仿真1是不考虑偏心销时的仿真结果，仿真2是计及偏心销对仿真影响的结果曲线。

图5 E点的位置变化Fig.5 Motion of Point E’s position

由图5得到的计算和仿真曲线可知，在伸爪过程中E点坐标、OE距离LOE及其转角的变化趋势基本保持一致。其中，OE距离LOE持续增大，E点的运动规律在构型变化处发生改变，LOE增长变缓直至伸爪运动结束。计算和仿真1的E点坐标分别为(-193.2 mm,229.6 mm)和(-193.0 mm,229.6 mm)，定位偏差为(-0.2 mm,0 mm)；计算和仿真1的LOE长度范围分别是188.4～300 mm和189～300 mm，变化裕度分别为111.6 mm和111 mm，平均偏差为0.3 mm；计算和仿真1的LOE转角范围分别为69.093 1°～130.080 5°和69.445 8°～130.048 9°，变化裕度分别为60.987 4°和60.603 1°，平均偏差转角0.192 15°. 仿真2得到的运动结束时刻E点坐标为(-187.7 mm,232.9 mm)，与计算值和仿真1的定位偏差分别为(-5.5 mm,3.3 mm)和(-5.3 mm,3.3 mm)；仿真2的LOE长度范围分别是189～299.1 mm，变化裕度为110.1 mm，相对于计算值和仿真1的变化裕度偏差分别为-1.5 mm和-0.9 mm；仿真2的LOE转角范围分别是69.564 0°～128.760 5°，变化裕度为59.196 5°，相对平均偏差转角分别为1.790 9°和1.406 6°. 由计算和仿真对比分析可知，二者仍存在一定误差，但误差较小；在考虑偏心销时得到的仿真曲线2与计算曲线以及仿真曲线1的对比可知，E点的运动轨迹存在波动现象。

3.2 动力学特性曲线

由ADAMS软件样机仿真可得到图6所示的有无偏心销时钩爪质心S2在全局坐标系的转角加速度变化曲线，并对有偏心销时转角加速度曲线进行了拟合。

图6 质心转角加速度曲线Fig.6 Curves of center of mass’s angular acceleration

由图6可知：无偏心销机构的钩爪质心S2点在全坐标系的转角加速度存在正负值变化，并在构型变化处有阶跃现象；在考虑偏心销时，加速度曲线存在波动现象，并对波动曲线进行了拟合，得到拟合曲线，拟合线的变化趋势与无偏心销时的加速度仿真曲线在变化趋势上基本一致，但也有一定程度的差别，尤其是在构型变化位置的加速度变化，偏心销的存在能有效降低加速度的突变。

4 结论

本文通过简化模型、建立系统方程和算例分析，进行了间歇式含钳爪回转机构伸爪运动的计算和仿真研究。得出以下主要结论：

1)机构在完成伸爪运动过程中存在构型的变化情况，第1个阶段是正4杆机构向反4杆机构的运动，第2个阶段是曲柄滑块机构。

2)伸爪过程中LOE的理论转角变化为60.987 4°，仿真结果分别为60.603 1°和59.196 5°，仿真与理论计算仍存在一定误差，但误差较小，误差原因主要来源于机构配合和尺寸等参数测量上的误差；E点的转角加速度在构型变化处发生突变，LOE持续增大直至伸爪运动结束。

3)分析偏心销对运动的影响由仿真可知，偏心销的存在会导致E点运动轨迹波动，但对钩爪定位误差影响较小；此外，偏心销能在减小加速度突变的同时会引起加速度振荡。