基于序贯蒙特卡洛与概率假设密度滤波的主动分布式声纳多目标跟踪

邵鹏飞， 王蕾， 王方勇

(杭州应用声学研究所 声纳技术重点实验室， 浙江 杭州 310012)

0 引言

分布式探测利用了空间分集的优势，有利于提高目标检测能力和定位精度，同时对跟踪检测融合算法也提出了更高的要求[1]，其中分布式声纳多目标跟踪模块是分布式声纳探测系统的一个核心要素，因此需要解决针对分布式探测模式的多目标跟踪问题。多目标跟踪可以看作为对目标状态集合的估计，需要解决目标不确实性和测量不确实性问题。目标不确实性包含目标状态及数目变化的不确实性，测量不确实性是指缺乏准确的目标背景环境先验信息及传感器观测过程中产生的随机性扰动，这些问题一方面可能因杂波过多而导致虚警过大，另一方面会因为未从测量中获取新生目标信息而导致漏检。目前常见的两类解决多目标跟踪器问题的方法有：1)基于数据关联的传统多目标跟踪方法[2-9]，包括最近邻方法[5]、联合概率数据关联方法[7-8]、多假设跟踪方法[9]等，该类方法的实质就是通过数据关联将多目标跟踪问题转化为多个并行的单目标跟踪器进行处理，然而该类方法计算量大，且需要较多先验信息和强约束条件，较难处理目标数目时变且未知的情形；2)基于随机有限集(RFS)的概率假设密度(PHD)滤波方法[10-19]，该方法建立在贝叶斯框架下，通过传递目标状态集合的1阶矩近似后验概率，通过序贯蒙特卡洛(SMC)方法[10-11,13-15]或混合高斯方法[12,19]递归实现目标预测与更新，该类方法可以解决数目时变的多目标跟踪问题。

本文主要研究基于SMC-PHD滤波的分布式声纳多目标跟踪技术，首先介绍了SMC-PHD多目标跟踪算法的理论基础，其次阐述了SMC-PHD多目标跟踪算法实现，最后针对分布式声纳测量仿真数据进行SMC-PHD多目标跟踪处理，并分析比较仿真结果，给出了该方法应用于主动分布式声纳目标探测的可行性。

1 SMC-PHD多目标跟踪算法

单目标系统的目标状态和测量是通过随机向量数学形式来表示的，而对于多目标系统，目标状态和测量通过RFS来表示。

1.1 RFS模型

在状态空间Es和测量空间Eo中k时刻的目标状态Xk和测量Zk[16-18]分别表示为Xk={xk,1,…,xk,M(k)}⊆Es，Zk={zk,1,…,zk,N(k)}⊆Eo，M(k)为k时刻目标数目，N(k)为k时刻包含了观测到的杂波和目标数目之和。在多目标系统下，RFS模型考虑了目标数量时变、测量杂波等不确定因素，k时刻的多目标状态RFSΞk包含了k时刻生存的目标状态RFSSk(Xk-1)、由上一时刻目标分化的新生目标状态RFSBk(Xk-1)及自发的新生目标状态RFSΓk；k时刻测量RFSΣk则包含了由k时刻目标状态产生的测量RFSΘk(Xk)及杂波测量RFSCk. 多目标状态RFS与测量RFS通过集合的形式表示为Ξk=Sk(Xk-1)∪Bk(Xk-1)∪Γk，Σk=Θk(Xk)∪Ck.

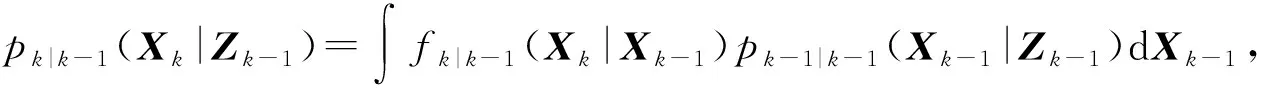
1.2 SMC-PHD滤波算法

对于像泊松点随机过程这样的计数过程，其1阶统计矩可以直接表示过程的密度函数或强度函数。因而，为了降低贝叶斯滤波传递表示全概率后验密度的复杂度，将RFSΞ的PHD表示为多目标后验密度的1阶期望形式[20]：

(1)

式中：δy(x)表示将测量观测建模为随机点过程，目标状态变量x聚集在观测测量变量y的狄拉克函数；PΞ(·)表示在多目标状态RFS下的多目标概率密度函数；X表示多目标状态。

由1.1节中RFS贝叶斯滤波的递归过程可以得到相应的PHD预测和更新方程，PHD预测算子Φk|k-1定义为

(2)

式中：α(·)表示在状态空间Es上任一可积分函数；γk表示k时刻自发新生目标状态RFS的强度函数；φk|k-1(x,ξ)=bk|k-1(x|ξ)+ek|k-1(ξ)fk|k-1(x|ξ)，bk|k-1(·|ξ)表示k时刻由之前目标状态ξ分化出的目标状态RFSBk(ξ)的强度函数，ek|k-1(ξ)表示k时刻之前目标状态ξ仍然生存的概率，fk|k-1(·|·)表示目标的转移概率密度函数。PHD更新算子Ψk定义为

(3)

式中：υ(x)=1-PD(x)，PD(x)为检测概率；Zk表示k时刻分布式多平台测量向量；ψk,z(x)=PD(x)·gk(z|x)，gk(·|·)为目标在k时刻的似然，z表示测量变量；κk(·)为k时刻杂波RFS的强度函数；〈·,·〉表示内积算符。

由于PHD滤波计算过程中涉及多个非闭合区间的积分，因此可以引入以随机样本近似概率分布的SMC方法，使PHD滤波在数值上可近似求解。SMC-PHD算法[16-20]可以分为如下步骤：

1)初始化。粒子在被观察区域初始化为均匀分布。

2)预测步骤。该步骤分为重要性采样及预测权重计算，其中重要性采样为

预测权重计算表示为

SMC-PHD算法的状态- 权重传递流程示意图如图1所示。

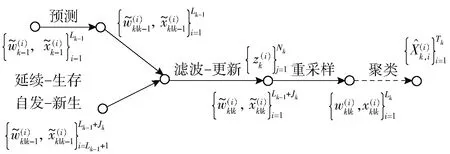
图1 SMC-PHD算法的状态- 权重传递流程示意图Fig.1 Flow chart of state-weight transfer of SMC-PHD algorithm

2 目标动力学与主动分布式声纳观测线性高斯模型

目标的运动状态主要包含目标的位置及运动速度，考虑声纳工作环境下水平与深度的尺度差异性较大，且深度变化的范围相对有限，因而本文将目标建模为二维水平观测下线性高斯的动力学状态方程，表示为

xk=Fxk-1+Gnk，

(4)

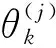
(5)

(6)

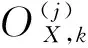
3 仿真分析

图2 观测平台4个节点与5个目标态势Fig.2 Situation of 4 observation platform nodes and 5 targets

图3为平台1在80 min内随时间变化的方位- 距离测量结果。由图3可知，由于杂波数目较多，单平台观测下的目标连续方位及连续距离变化历程较模糊，面临检测虚警高、目标定位精度低等问题。

图3 平台1观测结果Fig.3 Observation results of Platform 1

以图3所示观测结果作为SMC-PHD跟踪算法的输入，图4给出了相应的单平台跟踪滤波结果。图4(a)为某一时刻预测粒子与滤波粒子的权重分布，若粒子点越聚集，则概率方差越小，估计精度也更高；图4(b)为重采样后的粒子状态- 权重分布；图4(c)给出了仿真条件下真实的多目标运动轨迹；图4(d)为本文提出方法实现的单平台多目标跟踪轨迹输出结果。从图4中可以得出，单平台观测下似然函数无法表征多目标状态与杂波的充分统计信息，SMC-PHD算法处理过程中预测与滤波的粒子分布分散，导致重采样后对应多个目标的粒子不可分辨，故跟踪输出的目标位置估计误差较大，无法形成清晰的目标轨迹。

图4 单平台SMC-PHD跟踪处理Fig.4 Tracking processing of single platform SMC-PHD

图5描述了单平台观测下SMC-PHD跟踪算法输出的估计目标数目与真实目标数目随时间变化情况。从图5中可以得出，单平台观测下的SMC-PHD跟踪算法输出的估计目标数目普遍相对于真实目标数目偏大，原因是由于杂波相对于目标数目多，且单平台跟踪性能有限，导致跟踪- 检测的虚警率较高。

图5 单平台SMC-PHD跟踪算法输出的目标数目估计值与真实目标数比较Fig.5 Estimated targets number of single platform SMC-PHD tracking algorithm versus real targets number

图6给出了单平台观测条件下跟踪精度随时间变化的情况，其中：图6(a)与图6(b)分别为估计目标位置X轴、Y轴坐标分量随时间变化的结果；图6(c)为多目标跟踪误差(Wassertein距离)随时间变化结果，若Wassertein距离值越大，多目标估计性能越差。由图6中可以得出，不同时刻下目标坐标位置估计结果误差较大，且在不同时刻的多目标状态估计误差距离大多在5～10 km之间范围，主要原因是受杂波影响，导致跟踪虚警增大，误差距离增大。

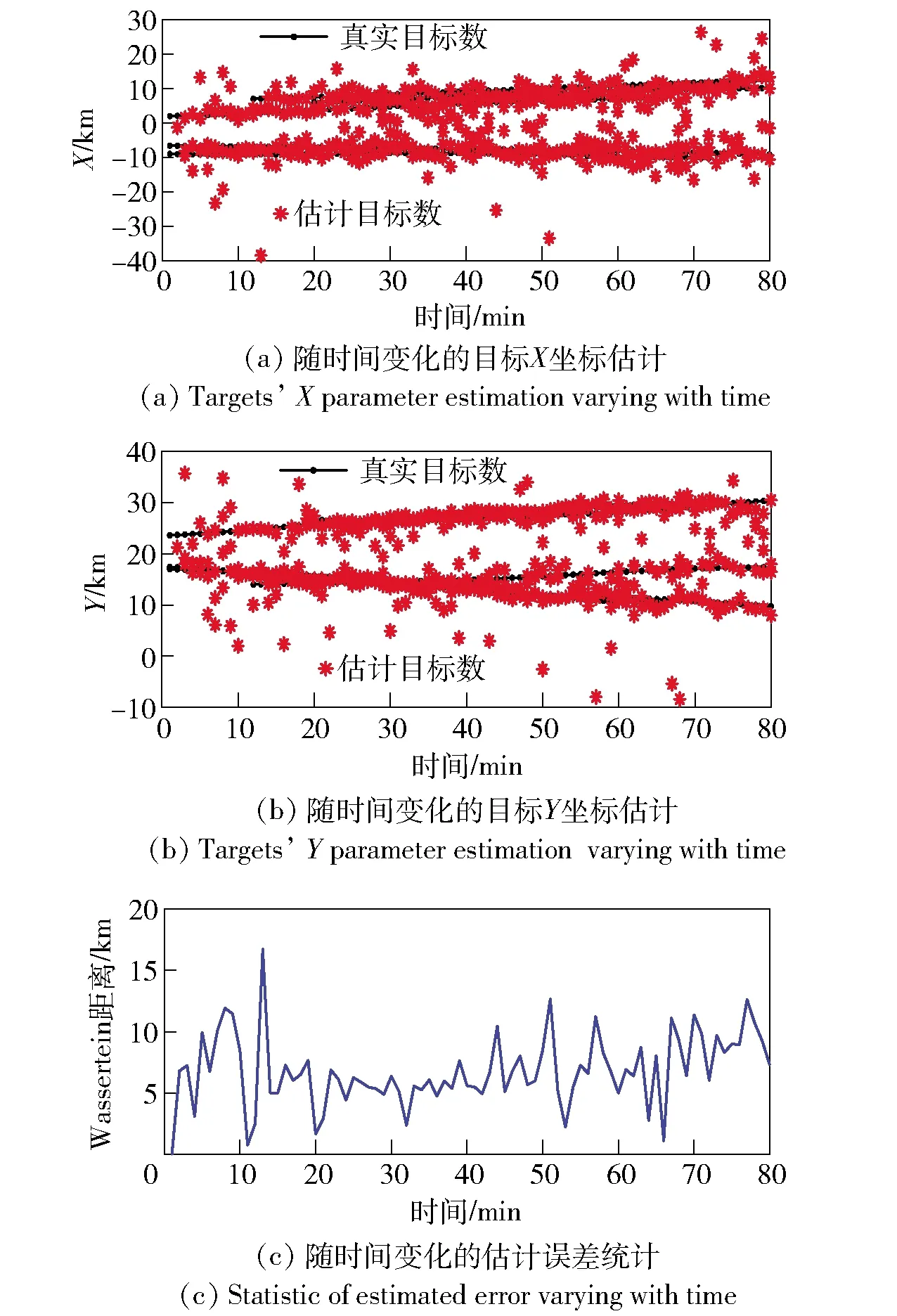
图6 单平台SMC-PHD跟踪算法输出随时间变化的目标位置估计及对应的估计误差分析Fig.6 Estimated time-varying target positions of single platform SMC-PHD tracking algorithm and corresponding estimated errors

图7给出了双平台观测下的跟踪滤波结果，其中，图7(a)为某一时刻预测粒子与滤波粒子的权重分布，图7(b)为重采样后的粒子状态- 权重分布，图7(c)给出了仿真条件下真实的多目标运动轨迹，图7(d)为利用本文方法实现的双平台多目标跟踪轨迹输出结果。由图7中可以得出，双平台观测下SMC-PHD算法处理过程中预测与滤波的粒子分布相对于单平台更集中，跟踪输出的目标位置估计可以形成可辨别的轨迹轮廓，然而由于估计的方差较大导致多目标轨迹模糊。

图7 双平台SMC-PHD跟踪处理Fig.7 Tracking processing of two-platforms SMC-PHD

图8描述了双平台观测下SMC-PHD跟踪算法输出的估计目标数目与真实目标数目随时间变化情况。比较图8与图5可以发现，双平台观测下的SMC-PHD跟踪算法输出的估计目标数目准确度相对于单平台提高甚为明显，仅在第50 min时出现一次估计值偏大情形。

图8 双平台SMC-PHD跟踪算法输出的目标数目估计值与真实目标数比较Fig.8 Estimated targets number of two-platforms SMC-PHD tracking algorithm versus real targets number

图9给出了双平台观测条件下跟踪精度随时间变化的情况，其中：图9(a)与图9(b)分别为估计目标位置X轴、Y轴坐标分量随时间变化的结果；图9(c)为多目标跟踪误差(Wassertein距离)随时间变化结果，若Wassertein距离值起伏较大，则可能出现了跟踪目标丢失(漏报)、跟踪目标为杂波(虚警)等跟踪不连续情形。比较图9与图6可以发现，相比于单平台观测，双平台观测下的SMC-PHD跟踪算法输出不同时刻下目标坐标位置估计结果误差明显下降，跟踪虚警明显减少，但受单平台测向- 测距性能影响，两平台对目标状态的估计性能受限，仍有较多时刻多目标状态估计误差距离明显偏大。

图9 双平台SMC-PHD跟踪算法输出随时间变化的目标位置估计及对应的估计误差分析Fig.9 Estimated time-varying target positions of two-platforms SMC-PHD tracking algorithm and corresponding estimated errors

图10给出了4平台观测下的跟踪滤波结果，其中，图10(a)为某一时刻预测粒子与滤波粒子的权重分布，图10(b)为重采样后的粒子状态- 权重分布，图10(c)给出了仿真条件下真实的多目标运动轨迹，图10(d)为利用本文提出方法实现的4平台多目标跟踪轨迹输出结果。由图10可以得出，4平台分布式观测下，SMC-PHD跟踪算法输出的目标位置估计结果准确，且目标轨迹清晰可辨。

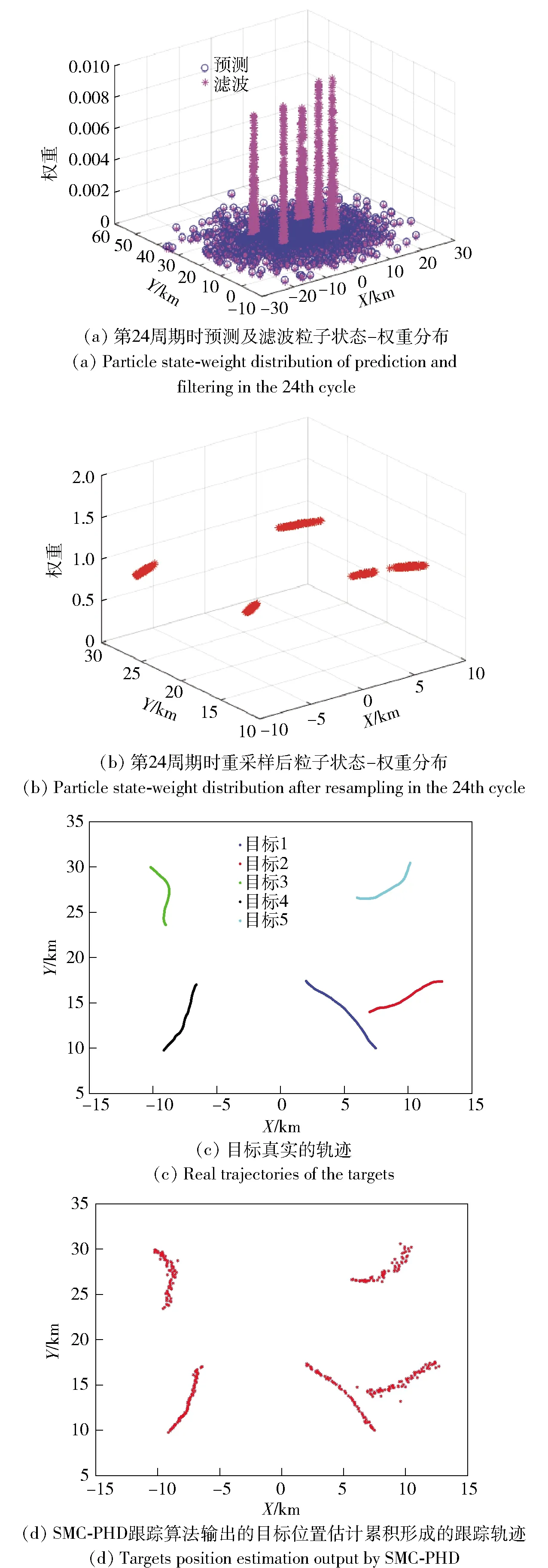
图10 4平台SMC-PHD跟踪处理Fig.10 Tracking processing of four-platforms SMC-PHD

图11描述了4平台观测下SMC-PHD跟踪算法输出的估计目标数目与真实目标数目随时间变化情况。由图11中可以看出，在4平台观测下，SMC-PHD跟踪算法输出的估计目标数目与真实目标数目完全一致。

图11 4平台SMC-PHD跟踪算法输出的目标数估计值与真实目标数比较Fig.11 Estimated targets number of four-platforms SMC-PHD tracking algorithm versus real targets number

图12给出了4平台观测条件下跟踪精度随时间变化的情况，其中，图12(a)与图12(b)分别为估计目标位置X轴、Y轴坐标分量随时间变化的结果，图12(c)为多目标跟踪误差(Wassertein距离)随时间变化结果。由图12与图9比较可以发现，相比于双平台观测，4平台观测下的SMC-PHD跟踪算法输出不同时刻下目标坐标位置估计结果误差进一步下降，仅有少量时刻估计状态误差偏大。

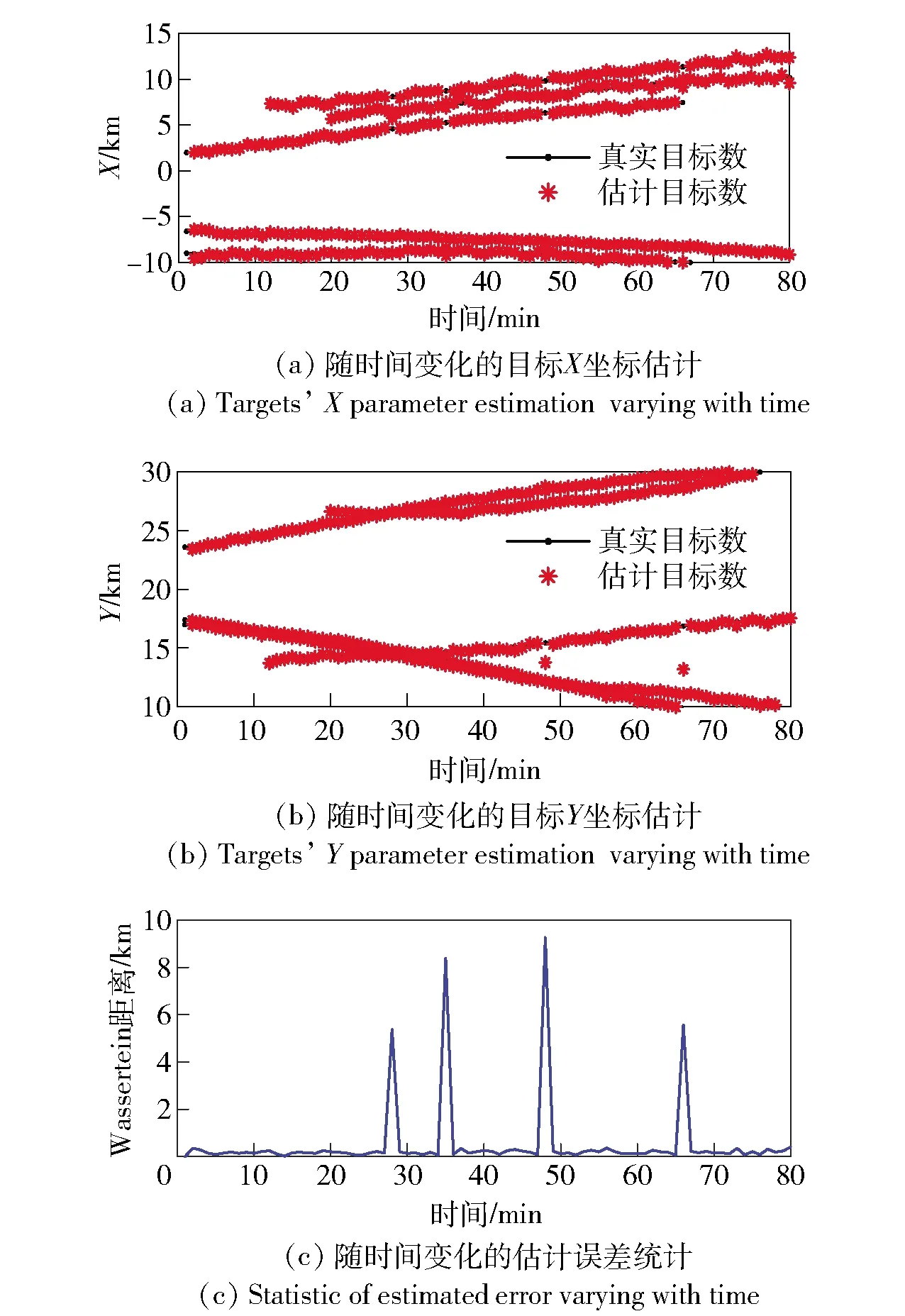
图12 4平台SMC-PHD跟踪算法输出随时间变化的目标位置估计及对应的估计误差分析Fig.12 Estimated time-varying of target positions of four-platforms SMC-PHD and corresponding estimated errors

4 结论

本文针对主动分布式声纳系统提出了一种利用SMC-PHD滤波解决高杂波环境下的主动分布式声纳多目标跟踪方法，并给出了算法实现流程，分别针对不同节点数目规模情形下进行主动声纳多目标跟踪仿真分析比较。得出以下主要结论：

1)单平台观测条件下，本文方法对多目标跟踪精度较差，虚警较高，无法准确估计目标数目并形成多目标运动轨迹。

2)双平台观测条件下，本文方法可以较准确估计目标数目，但是对于目标状态估计误差较大，目标运动轨迹较模糊。

3)4平台观测条件下，本文方法可以准确估计目标数目，对目标状态估计精度高，能实时输出清晰的目标运动轨迹。

综合结果表明：本文采用的SMC-PHD跟踪算法更适用于节点数目规模较大的主动分布式声纳系统，能在高杂波环境下实现对数目未知且时变的多目标自动跟踪；该方法数学理论清晰，实现流程简单，具有较好实时性，为发展集群化分布式融合探测等应用情景提供了有利支撑。接下来还需要进一步研究基于SMC-PHD贝叶斯滤波处理框架下的分布式声纳阵位优化、分布式声纳多目标估计性能限分析等内容。