GPD在地球化学元素异常识别中的应用
2020-06-17秦飞龙颜文勇周仲礼
秦飞龙,刘 剑,颜文勇,周仲礼,龚 灏,郭 科
(1.成都工业学院 大数据与人工智能学院,成都 611730;2.成都工业学院 汽车与交通学院,成都 611730;3.成都理工大学 数学地质四川省重点实验室,成都 610059)
地球化学元素含量异常指的是在某个区域或空间内,地球化学元素含量的空间分布与正常的地球化学含量分布模式产生偏离[1]。地质环境、构造背景、岩石类型等决定了地球化学元素异常的性质,厘清地球化学异常分布规律及其何种元素异常形成矿床,就能够有效进行深部矿产预测[2]。选取地球化学异常提取方法需要充分考虑异常分布特性,才能符合实际地质工作。因此,选取合理的方法提取地球化学异常至关重要。但由于地球化学异常形成的环境十分复杂,迄今并未有适用于各种地质环境下的地球化学元素含量异常求取方法[3-4]。如传统的三倍均方差法、概率格纸法、累计频率方法等在异常提取时要求样本数据满足正态分布;然而采集到的地球化学元素数据由于受到各种环境干扰,其分布规律并不呈正态分布[3]。分形方法近年来被广泛应用于地球化学异常提取,也有诸多成功的应用实例;但该方法需要建立在矿化信息基础上[5]。地球化学异常在地质空间中是后尾分布[6],而极值理论是对事件的超常大(或超常小)的随机性状进行研究,估计在已有观测水平上更为极端事件的概率[7],赵鹏大院士曾将其描述为极值[8]。因此,地球化学异常的分布特性符合 极值理论(EVT)研究范畴,并且 EVT 中的广义帕累托分布(GPD)正是对数据的后尾性特征进行刻画[9]。本文探讨利用极值理论的 GPD 研究地球化学元素含量异常空间分布规律,进行矿产预测,为深部矿产预测提供方法支撑。
1 地质背景
本文的研究区为湖北大冶鸡冠咀铜金矿床,矿床面积约为 2.18 km2,位于长江中部和中下游的Cu、Au、Fe成矿带以西,坐标是114°54′42″~114°55′45″E,30°04′45″~30°05′50″N,为第四系隐伏矿床[1]。截止到 2019 年 10 月,在研究区内共勘探到Ⅰ、Ⅱ、Ⅲ、Ⅶ主矿体群。矿体长度约为 950 m,宽度为160~800 m,深度为 5~1 412 m;在水平方向上,矿体投影面积约为 0.58 km2,倾向为北东 15°~72°,某些局部为北西西向[1]。Ⅰ、Ⅱ、Ⅲ、Ⅶ主矿体群为雁列状排列,倾向北西,局部倾向南[2]。主矿体主要分布在大理岩和侵入岩之间的断裂接触部位,并且还富集有大量的石榴石矽卡岩,在断裂带内闪长岩、角砾岩发育[1]。F1和 F3两条主断裂将研究区分为4个成矿部分(图1)。Ⅶ号矿体为研究区的主矿体,在 22 号勘探线与 34 号勘探线之间,深度从 447 m 开始,赋存十分丰富,具有巨大的找矿潜力[2]。因此,本文选取Ⅶ号矿体中 26 号勘探线 Mo、Ba、Zn 地球化学元素含量进行异常识别研究,探索新的矿体靶位。
2 GPD模型设计
2.1 GPD理论基础
GPD 分布是对大于某个观测值的样本数据进行分布拟合,刻画数据的后尾分布,也称为阈值模型[10]。如果数据x1,x2,…,xn是服从同一分布的独立随机变量序列,在样本数据中存在足够大的正数数据μ,则超过μ的分布定义为
(1)
式中:μ为样本数据的阈值;ξ为模型的形状参数;β为模型的尺度参数。如果ξ<0 时,则μ≤x≤μ-β/ξ;ξ≥0 时,x≥μ。在实际数据处理中,(2)式应用更为普遍。
(2)
如果β=1,(1)和(2)式称为 GPD 的标准形式。对(2)式求导,可得出GPD分布的密度函数
(3)
在(2)和(3)式中,取尺度参数β=1和形状参数ξ=-0.5,0,0.5,得出 GPD 的标准分布函数图(图2-A)和概率密度函数图(图2-B)。由图2-A知,当形状参数ξ由正值向负值变换时,GPD 分布的尾部逐渐变细。如果ξ<0,GPD主要分布在[0,-1/ξ] 内,形状参数ξ越小,区间越窄;如果ξ>0,GPD后尾性越明显,形状参数ξ越大,区间越厚。由图2-A知,GPD 的概率密度函数严格单调递减。
由式(1)和(2)知,GPD模型的确定需要估计形状参数、尺度参数和阈值。下面对对模型的阈值和参数进行估计。
2.1.1 阈值估计
GPD的阈值估计目前并没有精确的方法。在众多方法中,平均超出量函数E(μ)(MEF)是最为有效且应用较广的阈值估计方法[2],它是根据阈值μ和E(μ)的变化趋势进行阈值估计。
如果样本数据x1,x2,…,xn为独立同分布的随机序列,μ为阈值,当xi>μ,称xi-μ为超阈值量,如果给定样本数据的初始阈值为μ0,那么对任意阈值μ:μ>μ0,平均超出量函数E(μ)[11]定义如下
E(μ)=E(x-μ|x>μ)
(4)
进行积分得
(5)
如果ξ<1,积分收敛,极限为0;
如果0<ξ<1,E(μ) 为
(6)
由式(6)知,E(μ)是关于μ的线性函数。
在实际数据处理中,E(μ)常常利用如下统计方法进行计算[2]
(7)
式(7)中:n为样本的个数,N+为>μ的个数;(xi-μ)+为高于μ的第i个样品超过阈值量,也称损失量。
对于一组数据,如果阈值μ0已知,那么,任意的x>μ0都符合GPD分布,并且由上面理论知{(x,E(x)):μ0
2.1.2 估计形状参数和尺度参数
在GPD分布中,估计参数的方法较多,但是精度不高,目前应用最广且较为有效的估计方法包括最大似然函数法[12]和矩法估计[1],具体如下:
a.极大似然函数法
在GPD分布中,通过对方程(2)两边取导数,得GPD的概率密度函数为
(8)
同时对(8)式两边取自然对数,得对数似然函数
L(ξ,β:x)=-nlnβ-
(9)
在对数似然函数(9)式中,求取关于参数ξ和β的偏导数,得出如下的对数似然方程
(10)
b.矩法估计
在GPD分布中,利用矩法估计也可以得出形状参数ξ和尺度参数β,并且其估计精度优于极大似然函数方法。因为矩法估计是利用数据的样本矩反映数据的总体矩,它不会因为GPD形式不一样而得到不同的参数值[1]。矩法估计表达式如下
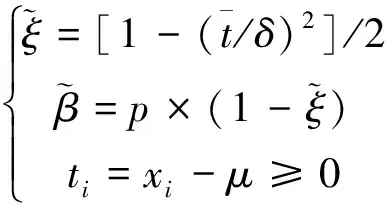
(11)
其中:p,δ分别是ti的均值与标准差;xi为样本数据。
2.2 地球化学异常 GPD 模型构建
由于地球化学数据X={x1,x2,…,xn} 的异常值位于观察数据尾部,GPD研究的是高于某足够大的阈值数据的后尾分布规律,本文利用GPD分布建立地球化学异常提取模型。由上述的相关理论可知,通过矩法估计求出地球化学数据的GPD分布的形状参数和尺度参数,再利用平均超出量函数MEF估计数据的阈值,从而得出地球化学数据GPD分布。具体如下:
① 获取数据X。
② 数据后尾性检验:利用QQ图或PP图检验地球化学数据是否具有后尾特性,利用 ADF (Augmented Dickey-Fuller) 检验数据的平稳性。
③ 参数估计:利用(11)式求出 GPD 分布中的参数。
④ 估计阈值:在X中选择不相同的阈值μ,通过式(7)得出超额均值函数E(μi),其中μi∈μ。绘制(μi,E(μi))的散点图,如果出现某个阈值μ0,当μ≥μ0,E(μ)关于μ是一个近似的线性函数,那么μ0就为异常值,亦为地球化学元素含量异常下限值。
⑤ 确定异常数据GPD分布:将得出的参数和阈值代入(2)或(3)式中,得出地球化学元素含量异常的GPD分布。
⑥ 结果检验:模型确定后,需要进行诊断性检验来确定求出的模型分布与实际分布是否吻合,如果效果不佳,返回第④步,估计新的阈值。诊断性检验常用的方法有PP图和QQ图。
在以上构建的异常提取模型中,阈值选取必须要合理,如果模型的阈值估计较高,则后尾数据xi(xi>μ;i=1,2,…,n)变少,造成后尾数据整体较大,影响参数估计的敏感性,使得方差变大;反之,阈值较小,后尾数据量增多,有利于提高GPD参数估计的精度,但存在部分数据并不符合GPD分布。并且,后尾数据量增多,数据的中心发生变化,使得估计值与理论值具有一定的差异。
尽管MEF在估计阈值μ上具有计算快、比较直观等优势,但仅仅通过线性方式进行阈值估计存在一定的缺陷。第一,该方法是在某个小区间范围内选取阈值,不能确定某一具体异常下限值,会造成地球化学元素含量异常分布区域过大及过小的问题,给实际勘探带来困难;第二,如果出现2个阈值μ1和μ2,使得平均超出量函数都呈现线性,可以选择线性关系明显的地方作为阈值。但是线性不明显,选取就存在困难。因此,本文在MEF原理基础上进行了一定的修正,得出了一种更为稳健的修正阈值法确定阈值,具体如下:
根据广义帕累托分布原理,只要确立了某个阈值,对于所有阈值μ(μ>μ0),样本数据的 GPD分布的形状参数和尺度参数是不会改变的,并由极值类型定量[13]可得
β(μ)GPD=δGEV+ξ(μ-μ0)
(12)
因此,对于μ>μ0,有
β(μ)=δ+ξ(μ0)或β(μ)=β(μ0)+ξ(μ-μ0)
(13)
如果令
β*(μ)=β(μ)-ξ(μ)
(14)
β*(μ) 不会随阈值μ的变换发生变化,本文将β*(μ)称为修正的阈值参数。因此,在某个阈值区间内,经修正函数拟合出β*(μ)不会随阈值μ发生变化的拐点μ0作为阈值,并且大于μ0的所有超出量均满足GPD分布。
2.3 GPD模型处理地球化学数据的有效性
本文所构建的地球化学元素含量异常提取GPD模型充分考虑了异常在地质中的实际分布特性。地球化学异常值相对于背景值来说,它是位于整个分布的尾部,具有后尾特性,反映了数据在超常大(或小)的随机形状特征。EVT是研究数据的统计规律,是统计学的一个分支,用来刻画数据的极值分布问题,并且EVT中的GPD正是对数据的后尾性特征进行刻画。因此,利用GPD分布刻画异常值的分布规律是完全可行的,并且本文还对阈值的选取设计了修正函数,能够确定数据的某一精准异常值,并已经进行了充分证明[1]。下面利用实际真实数据进行验证说明。
3 GPD模型分析原生晕地球化学元素异常分布规律
3.1 数据获取
为了体现本文模型的有效性,将其应用于研究区进行数据处理,选取Ⅶ号矿体26号勘探线上的Mo、Ba、Zn成矿元素的含量。3种元素的面含量随着深度的变化如表1所示。显然,深度越深,Ba含量有逐渐降低的趋势,Zn含量为逐渐升高的趋势,Mo随深度含量变化不大。从而,Ba为前缘晕元素,Zn为尾晕元素,Mo为近矿晕元素,也称主成矿元素。但是这3种元素实际上并没有表现为线性增加或减少(图3),而是出现了不同程度的中转,说明矿床表现出多期次的热液叠加现象。尤其是主成矿元素表现为强富集时,元素的前缘晕为强异常、尾晕为弱异常现象,指示深部还存在着盲矿体,为深部盲矿体预测提供了依据。
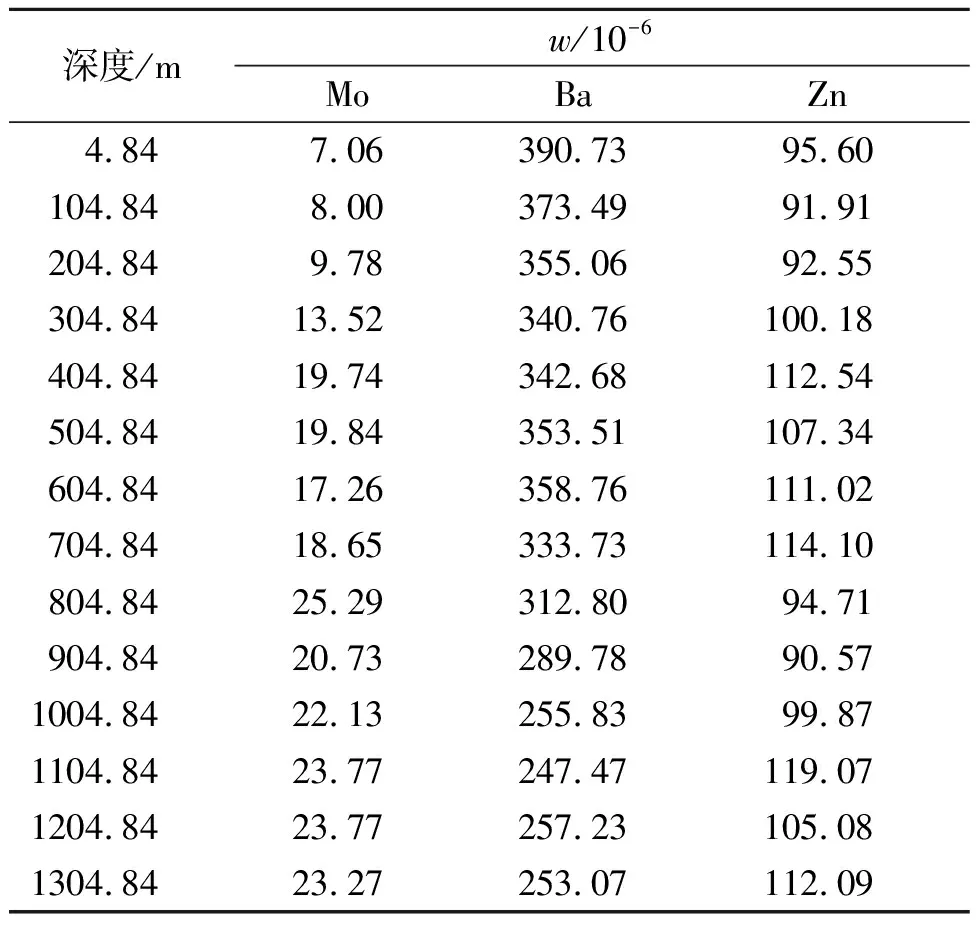
表1 元素的面含量Table 1 The surface content of metal elements
3.2 模型检验
3.2.1 数据后尾性检验
将Mo、Ba、Zn元素含量进行统计分析(表2),由统计结果知Mo、Ba、Zn元素的偏度分别为5.74、0.31、0.49,全部大于0,说明元素不满足正态分布,均为右偏;由变异系数知,Zn值最小、最稳定,Mo值最大、最不稳定;由峰度知,元素的峰度均高于正态分布值3,属于尖峰分布。由此,3种元素含量分布均为非正态分布,并且呈现尖峰、右偏特征。采用 QQ 图对数据进行后尾性分析(图4),发现3种元素仍是右偏。

表2 元素含量统计结果Table 2 The statistical results of element contents
3.2.2 数据平稳性检验
平稳性检验可以检验样本数据的自相关性。利用 ADF 法得出元素的平稳性结果如表3所示,显然,3种元素的t统计值均比1%的临界值(-3.43)低,无单位根,从而它们都是平稳序列。
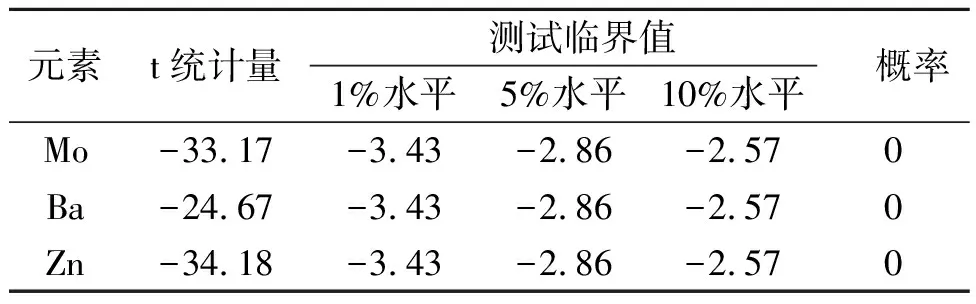
表3 元素含量的ADF检验Table 3 ADF test of element contents
通过上面分析,Mo、Ba、Zn元素均是后尾、非正态的平稳序列,完全满足所构建的GPD分布,从而利用所设计的模型进行异常提取。
3.3 模型求解
利用(11)式的矩法估计求出 Mo、Ba、Zn 元素的GPD分布的尺度参数分别为6.62、49.11、3.50,形状参数分别为0.37、0.17、0.31。根据(7)式绘出Mo、Ba、Zn元素的超额均值函数图(图5),通过超额均值函数图可以确定Mo、Ba、Zn元素分别在区间[35.86,38.23]、[378.41,388.73]、[135.21,140.18]以后,MEF为斜率>0的线性函数。因此,上述区间为地球化学元素含量的初始阈值区间。现在利用本文设计的修正函数确定具体的异常下限值,将这3个区间分别均匀地插入N个数,插入个数越大,阈值越精确,一般选取50个点就可以达到精度要求[2]。本文在3个区间上分别均匀插入50个点,由修正尺度函数β*(μ)得出3种元素的含量分别在36.29、382.56、138.47后,函数的ξ和β*(μ)值不再变化(图6、图7)。由前面的叙述可知Mo的异常下限为36.29,Ba的异常下限为382.56,Zn的异常下限为138.47。
利用(1)式得出3种元素含量GPD分布为
当元素含量的GPD分布确定后,利用诊断性检验判别所求模型是否合理,通过PP图得出元素异常含量实际数据与GPD分布拟合结果如图8所示。由图8知,元素含量的实际分布均拟合在直线周围,拟合效果较好。元素含量的理论分布和实际分布吻合,建立的模型具有有效性,阈值选取准确,能够利用所求结果进行元素含量异常空间分布和矿产预测。
3.4 原生晕地球化学元素异常分布
相应的地质剖面底图由湖北省地质局第一地质大队提供(图9)。确定元素异常下限后,利用 MapGIS 得出3种元素在地质体中的异常分布图(图10、图11、图12)。由这3张图可知,本文构建的GPD异常提取模型得出的元素含量异常的空间分布规律与矿体走势吻合, GPD 模型确定的元素含量异常分布规律(图10)和经典的累计频率方法得出结果吻合(图13),并且精度更高。说明本文的模型合理。根据元素空间分布规律发现,前缘晕 Ba 元素不仅在矿体顶部富集,在矿体下部也存在富集现象(图11),该现象属于前缘晕反分带现象,说明深部可能有矿体存在;尾晕 Zn 元素主要在矿体尾部富集,但是在矿体上方有部分与前缘晕存在叠加现象(图12),说明 Ⅶ 号矿体具有多期成矿的地球化学特征,并且尾部元素分布和前缘晕共存,进一步说明深部盲矿体的存在;近矿晕 Mo 元素与矿体走势吻合(图10),尤其在矿体深部出现延伸现象,说明深部有盲矿体存在,特别是位于Ⅶ号矿体东南向下延伸端,钻孔 ZK02620 地下1 300 m 处,Mo元素具有向下和向右的强异常趋势,指示盲矿体存在,并经实际工程验证在该处发现了钼矿和铜金矿(2016 年钻孔 ZK02620 终孔)[1],进一步证明 GPD 确定的结果具有有效性。根据分布规律发现近矿晕元素在钻孔 KZK10 和钻孔 KZK11 深度 1 100 m附近有强异常富集。由于该处未采集到地化数据,造成该现象的原因很可能是位于钻孔 ZK2620 下的钼矿体延伸所致[1],再结合地质成矿规律确定此处可划为一个找矿靶区。
4 结 论
本文以实际地质为背景,结合GPD原理和地球化学分布规律,构建了地球化学异常提取模型,有利于深部地球化学找矿。主要结论如下:
a.本文在地化元素含量异常分布特性和GPD理论基础上构建了异常GPD提取模型,并且设计了一种修正阈值方法,避免了异常值过大或过小的影响,提高了异常提取精度。
b.将本文构建的模型应用于实际矿区进行异常提取,结果该模型能够有效提取元素含量异常下限值,并且通过元素含量异常分布规律得出了深部地球化学找矿标志:①近矿晕Mo 元素含量异常作为直接地球化学找矿标志;②前缘晕Ba元素不仅在矿体顶部富集,在矿体下部也存在富集现象,属于前缘晕反分带现象,说明深部有盲矿体;③尾晕、前缘元素同时在矿体中部和下部富集,说明在矿体深部具有向下延伸的可能性。
c.本文通过构建模型确定的元素含量异常分带和成矿地质条件,预测到研究区26线位于钻孔KZK10和KZK11深度 1 100 m下有找矿靶位。
本文研究成果得益于湖北省地质局第一地质大队提供原始数据,以及成都理工大学刘洪军教授、徐争启教授提出建设性的建议,作者借此向他们深表感谢。
