新冠肺炎非均匀感染力传播模型与干预分析

汪剑眉，李 钢

(北京邮电大学经济管理学院 北京 海淀区 100083)

新型冠状病毒肺炎(COVID-19，以下简称新冠肺炎)全球确诊病例已超过百万例，受疫情影响的国家和地区已达200 多个。疫情在中国得到有效控制，目前境内确诊病例仅有零星散发。在积极干预的背后，流行病传播动力学研究为趋势判断和防控决策提供了重要参考。早期研究受限于时间跨度短、干预成效未完全显现以及对病毒特性的认知局限。目前国内疫情态势渐趋明朗，具备了更完整的数据观测周期和更丰富的临床认知佐证，使研究具有更多优化和拓展空间。

本文以SIR 经典仓室模型为逻辑架构，设计了分群、分阶段的非均匀感染力扩展模型，对全国、湖北、武汉3 层次分形网络进行建模训练，通过降阶得到更有效的子过程迭代，在参数设置和精度优化方面有所突破。在各干预杠杆强度上下浮动20%的场景设定下模拟疫情发展进程，评估中国防控模式的成效，并为我国和全球其他国家的后续防控工作提供有益参考。

1 前期研究与启发

在建模和参数研究方面，文献[1]应用SEIR仓室模型以多重拟合确定参数，结合LSTM 模型对疫情趋势进行综合预测，在参数估计方面更贴近临床实践；文献[2]对仓室模型进行了扩展，增加无症状感染者A、被隔离易感者Sq等，采用M-H算法进行参数估计建模；文献[3]在这一研究的基础上通过欧拉数值方法进行参数优化；文献[4]根据吉布斯采样确定基本再生数，以国际确诊病例反推武汉感染人数，并针对感染力进行差异化分场景仿真；文献[5]通过蒙特卡罗方法模拟联合分布进行参数推断和预测，将研究限定在2020 年1 月23 日前武汉的无干预自由传播期，这种阶段划分有效区隔了病毒传播早期与中后期的显著不同。

在控制措施效果评估方面，文献[6]主要围绕人口流动性和确诊感染病例数之间相关性的变化，评估交通管制、切断本地传播链等举措成效；文献[7]将有效再生数作为评价防控效果的核心指标，基于蒙特卡洛方法以患者症状出现时间和世代间隔对有效再生数进行估计；文献[8]研究了个人防护、早期诊断收治和后期诊断收治3 种控制策略组合下病毒的扩散速度，通过构造目标函数并转化为哈密尔顿函数极小化最优控制问题，发现全面组合策略更有效。

上述研究为模型的优化和突破提供启发：1)在检疫隔离和集中收治等政策下各群体感染力不均匀，应考虑分群。2) 干预政策出台时间点附近疫情曲线呈现明显弯折，参数具有显著分段特征，各时段感染力不均匀，应考虑分阶段。3) 建模主体选择方面，根据国家卫健委疫情通报数据计算，2020 年3 月25 日之前湖北确诊病例中70%以上来自武汉，全国确诊病例中70%以上来自湖北，局部与整体具有分形网络自相似量化统计特征，如结合分形架构，可在参数估计时充分利用全国、省、市3 层次数据。4) 根据国家和湖北卫健委疫情通报数据计算，未感染者始终在国内人口中占据主体，武汉约99.56%、湖北约99.89%、全国约99.94%，如能将感染者和未感染者的迭代过程分离，可有效提高模型精度和效率。5) 可将接触、隔离、收治和治愈视为干预杠杆，模拟并观测其在加强和减弱两个方向上调节时疫情态势变化，从而描绘可干预空间、评估干预成效并实现横向可比。

2 方法与数据

2.1 模型逻辑架构

基于经典SIR 仓室模型[9]进行扩展，如图1 所示。为体现感染力异质性，根据人群流动自由度分群：

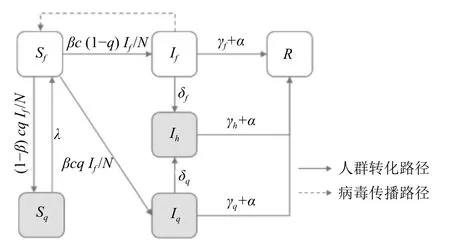
图1 SIR 非均匀感染力扩展模型的逻辑架构

S 为易感者(susceptible)，包括自由易感者Sf和隔离易感者Sq，对新冠肺炎人群普遍易感。

I 为感染者(infectious)，包括自由感染者If、隔离感染者Iq和收治感染者Ih，按其是否被隔离分别包含于If和Iq中，其中If主要包含潜伏期感染者及始终无症状感染者[10-11]。

R 为移除者(removed)，包括治愈者和病亡者。

感染路径仅有一条，即自由感染者If传染自由易感者Sf。人群转化路径包括以隔离效率系数q 监测并隔离有密切接触史或疑似症状的自由易感者Sf，如其未感染则成为隔离易感者Sq，并在隔离结束后再次成为自由易感者Sf(隔离解除率λ 为隔离期的倒数)；如其已感染则成为隔离感染者Iq。自由易感者Sf以接触效率系数c 和日感染率β 被感染，转化为自由感染者If。If和Iq继而以收治效率系数δ 转化为收治感染者Ih。三类感染者分别以治愈效率系数γ 及日病亡率α 成为移除者R。考虑分形架构，令i={1,2,3}分别表示武汉、湖北、全国3 个层次。模型微分方程如下：

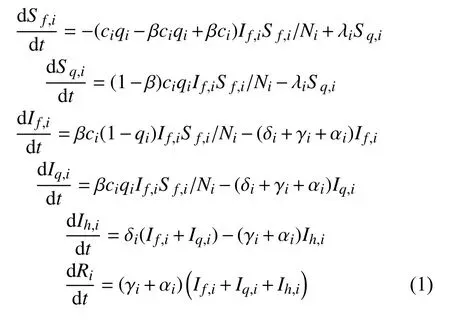
感染力为每位感染者的日均感染人数，即FOI=βcSf/N=R/DI(在干预初期为Ro/DI)。

病毒特性参数包括基础再生数Ro、世代间隔DI、日感染率β、日病亡率α，为不变参数，由病毒本身特性决定[12-13]，不随阶段改变而改变，其中前3 项参数在武汉、湖北、全国3 个层次保持一致，日病亡率α 考虑供给保障能力有所不同而保留差异。干预杠杆参数包括接触效率系数c、隔离效率系数q、收治效率系数δ、治愈效率系数γ，为可变参数，在不同阶段、不同层次具有不同的参数值，从而模拟空间分布上感染力的非均匀性。

一个完整的疫情周期需要经历自由感染者高峰、隔离和收治感染者高峰、移除者新增高峰，根据峰值点数据观测，将观察期划分干预初期(2020年1 月20 日−2 月4 日)、探索期(2020 年2 月5 日−2 月17 日)、 掌 控 期(2020 年2 月18 日−2 月27 日)、平 稳 期(2020 年2 月28 日 之 后) 4 个 阶段，从而模拟时间分布上感染力的非均匀性。

2.2 迭代矩阵降阶与子过程分解

时间步t 表示从起始日(1 月20 日)开始计算的第t 天，每日样本矩阵X=(Sf, Sq, If, Iq, Ih, R)。第t+1 步状态变量仅由第t 步状态变量决定，视为有限状态空间内的马尔可夫过程，x(t+1)=x(t)A，x(t)为n 维状态向量，A 为状态转移矩阵。因自由易感者人口占比超过99.5%，Sf/N≈1，则有：

分块降阶，则：

由此分离为两个子过程，即易感者迭代(Sf, Sq)A1、感染与移除者迭代(If, Iq, Ih, R) A4，对于疫情的模拟主要基于后者。两个子过程数据量级相差百倍以上(易感者与感染和移除者的数量比值武汉超过200 倍，湖北超过800 倍，全国超过17 000倍)，分离迭代有利于提高模型精度和计算效率。但子过程转移矩阵首行元素和不为1，不再是完整的马尔可夫过程。

2.3 数据来源与统计口径

数据来源为国家卫健委、湖北卫健委、武汉卫健委发布数据，并进行了两次修正。一是2020 年2 月12 日湖北确诊方式增加“临床诊断”，导致数据跃升，按确诊和临床病例比例对前序数据进行修正；二是2020 年1 月24 日9 家持有资质的医院和武汉市疾控中心获得检测授权，短期内大量积压待检病例得到确诊导致数据跃升，按平均增速对前序数据进行修正。

3 参数估计

3.1 病毒特性参数估计

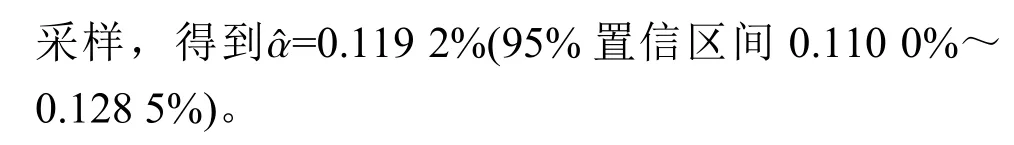
3.2 干预杠杆参数估计

在获得病毒特性参数估计值的基础上，干预杠杆参数估计转化为求各阶段线性定常系统状态转移矩阵的方程解析解。

通过分形理论的支持，如拓扑学和动力学领域时变曲线的无标度属性，可以综合利用武汉、湖北、中国3 个层次的统计数据进行参数估计。结合拟合特征，应用监督式机器学习GPR 高斯过程回归方法，将各时间步解向量作为样本对回归模型进行训练，得到4 个阶段的参数估计如表1 所示。

接触效率系数在干预初期受春节影响明显上浮，在交通管制、社区封闭等最大限度控制人口流动和聚集的应急干预下出现几何级数下降。隔离效率系数总体平稳略增，武汉以外区域优于武汉，湖北以外区域优于湖北。拟合周期主体处于医疗资源非挤兑期，全国实行统一诊疗方案、防控方案，收治效率系数在探索期出现短期提升，源于增加“临床诊断”和全面排查应收尽收。治愈效率系数随诊疗方案不断成熟而显著改善，通过提高医疗资源周转率，避免收治和隔离环节拥塞。

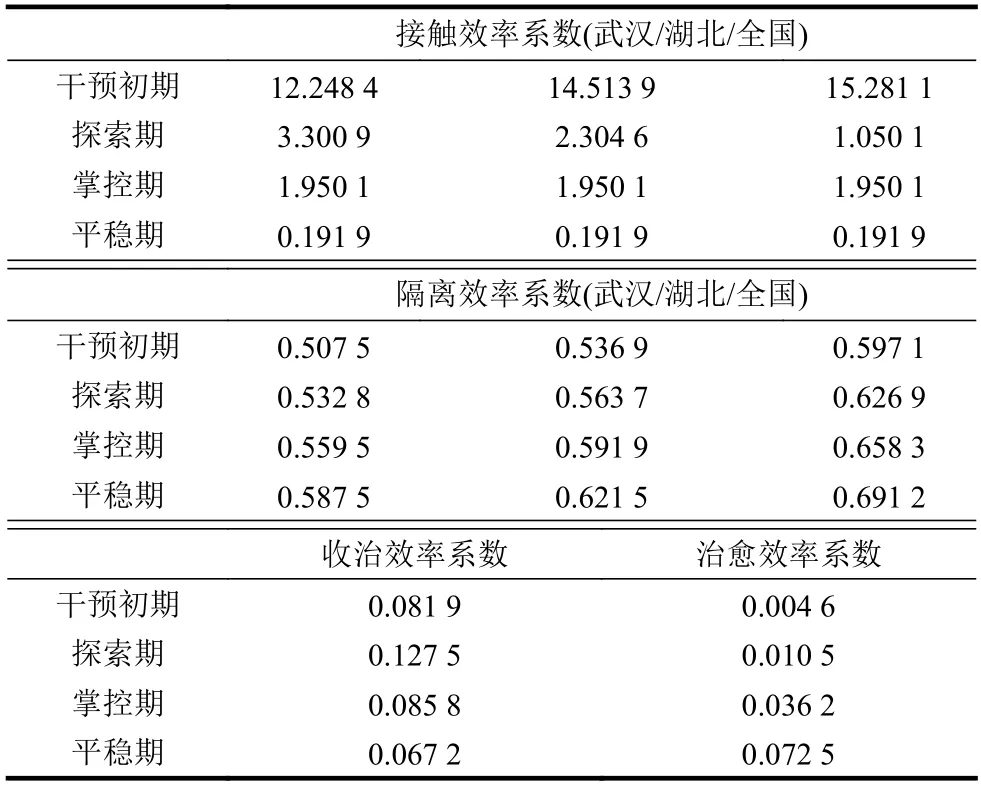
表1 干预杠杆参数估计均值

3.3 模型拟合

基于参数估计计算模型在各时期3 个区域层次的感染力均值如表2 所示。

表2 各阶段非均匀感染力FOI

模型对疫情发展实际趋势拟合良好，以此作为基础场景，如图2 所示。

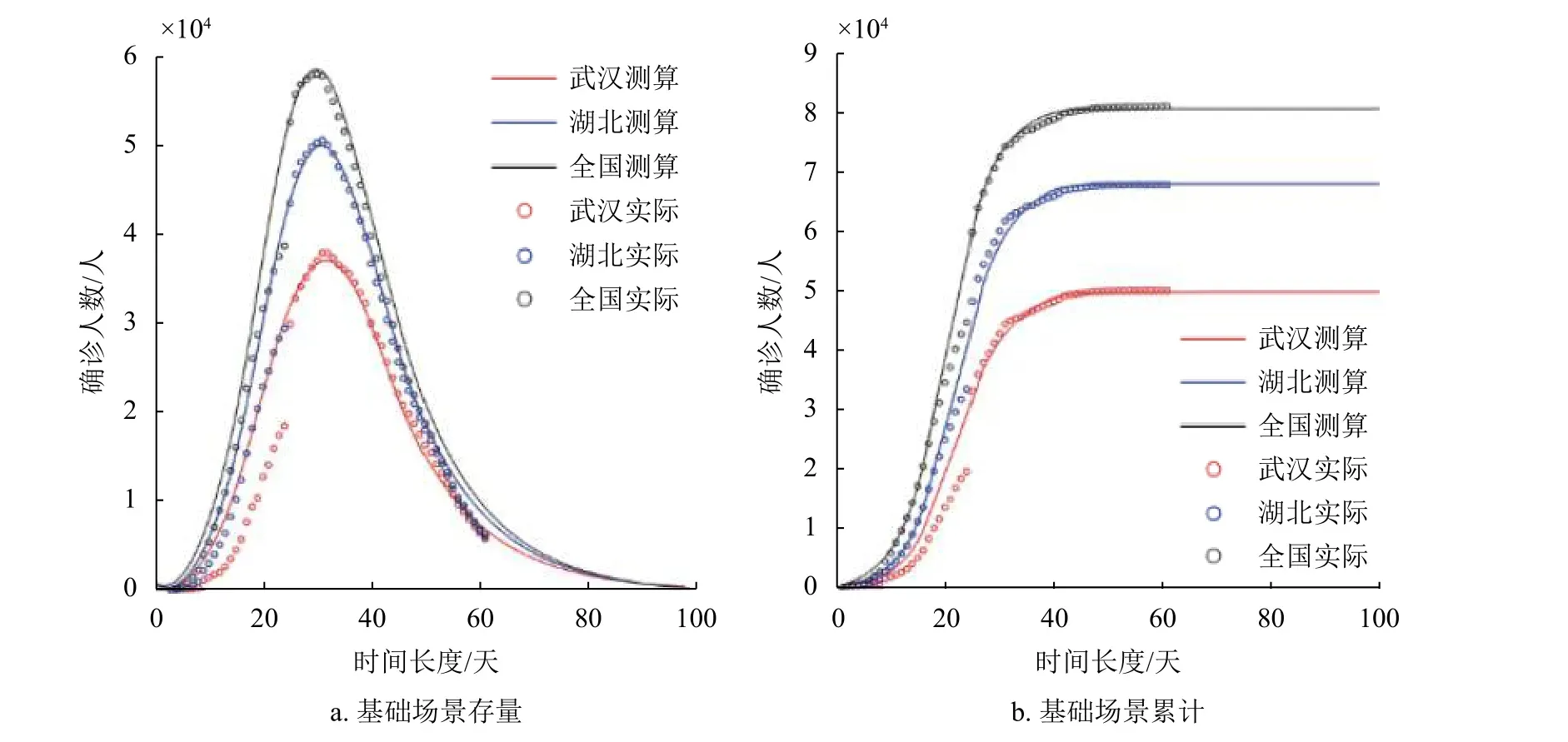
图2 基础场景模型预测与实际值比较

4 敏感度分析

分析疫情态势对干预杠杆参数变化的敏感度SAF[15]。态势变量包括感染者峰值规模NP、峰值周期TP、终值规模NF、终值周期TF。设杠杆参数为x，有：

以现有干预强度为基础场景，增强或减弱单项杠杆的强度，使其变化幅度达到20%，发现敏感度在趋强和趋弱两个方向上存在不对称的边际效应，弱干预场景下边际损失递增，强干预场景下边际收益递减，详见图3， If1/ If2/If3分别为武汉/湖北/全国自由感染者， Iq1/Iq2/Iq3为分别为武汉/湖北/全国隔离感染者， Ih1/Ih2/Ih3分别为武汉/湖北/全国收治感染者， R1/R2/R3为分别为武汉/湖北/全国移除者。

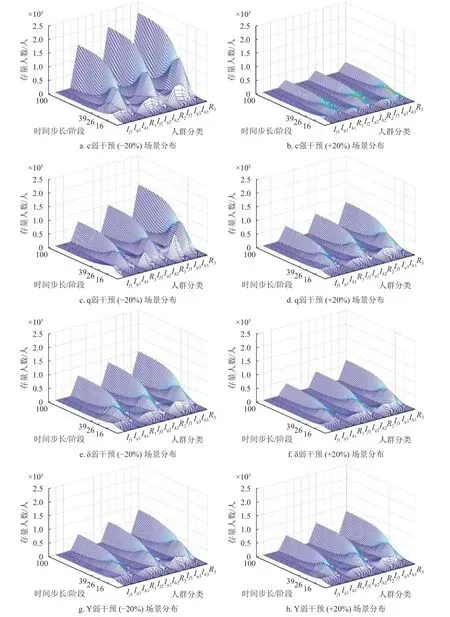
图3 干预杠杆参数的强干预场景与弱干预场景模拟分布

弱干预场景中，如人口流动性干预降低20%，全国可达21 万累计确诊规模；如对密切接触者和疑似者的隔离效率降低20%，全国可达15 万累计确诊规模；如集中收治效率降低20%，全国可达10 万累计确诊规模。强干预场景下，除降低接触和提高收治会使峰终值降至基础场景的37%和80%以外，加强其他两个杠杆对峰终值影响不大。表3 为干预杠杆参数的多场景调控幅度模拟值。

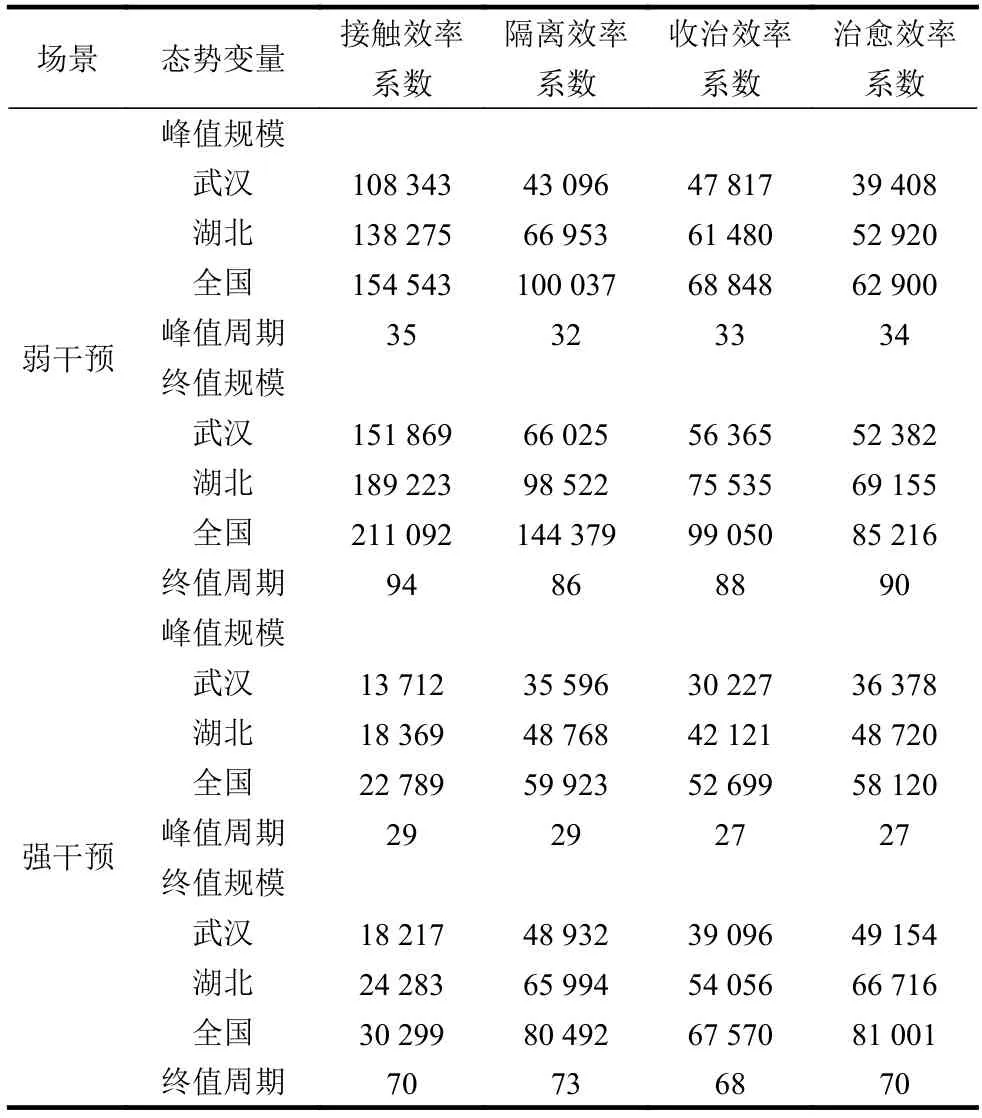
表3 干预杠杆参数的多场景调控幅度模拟值

表4 干预杠杆参数的敏感度

4 类干预杠杆中，降低接触是有效抑制疫情的核心杠杆，敏感度是其他干预杠杆的3.5 倍以上。隔离、收治、治愈属于防御型杠杆，可维持疫情态势平稳发展。

表4 为干预杠杆参数的敏感度值。弱干预敏感度提示了防控的重要风险点，降低接触是防止疫情失控的最基础手段；其次是隔离和收治，可避免峰终值过载；治愈可避免峰值周期不断拖延。强干预敏感度表明了主动防控的提升空间，降低接触是控制疫情规模和周期收效最为显著的手段，及时收治可以在一定程度上抑制终值规模。

5 结 束 语

根据模型的子过程解构，最大限度控制人口流动和聚集，对有效遏制疫情发挥了关键作用；通过增加“临床诊断”、全面排查、加大床位供给实现应收尽收，在短期内有力扭转了增长势头。

根据敏感度分析，强弱场景边际效应不对称，全程减弱干预会引发较大疫情风险，但加强干预只会带来较小疫情改善，证明中国方案比较接近准帕累托最优。虽然在降低接触和集中收治方面理论上存在优化空间，但实际受限于干预初期对病毒特性的发现与认知、探索期对医疗需求的刚性兑付、掌控期对社会管理的托底投入以及平稳期防疫与经济发展的再平衡。整体而言，中国模式干预杠杆组合有力有效。