在空间动态背景下要会建系解题

■钱浩鹏(指导老师：褚人统)

作者单位：浙江省天台中学2018级10班

大家在求解空间旋转类数学问题时，若仅凭直观感觉，则很难获得正确结论；若采用代数方法，则过程烦琐难解；若能建立合适的空间直角坐标系，将动态变化问题转化成向量问题，则能够获得清晰的解题思路，顺利求得最终结果。下列举例分析。

例1如图1所示，在△ABC中，AC⊥BC，BC=1，AC=a，D是AB的中点，将△BCD沿直线CD翻折，若在翻折过程中存在某个位置，使得CB⊥AD成立，则a的取值范围是____。

图1

解：建立空间直角坐标系及坐标标注情况如图2所示。在翻折过程中，始终有|BC|=1，|BD|=。当CB⊥AD，即时，有x2+，即，解得。

图2

评注：上述解法虽有一定的运算量，但思路清晰，思考量小，远胜于传统的思维方法。

例2如图3所示，在正方形ABCD中，E，F分别为线段AD，BC上的点，∠ABE=20°，∠CDF=30°。将△ABE绕直线BE、△CDF绕直线CD各自独立旋转一周，则在所有旋转过程中，直线AB与直线DF所成角的最大值为____。

图3

直觉推理：按照题意就会得到两个圆锥，即以BE为轴的圆锥和以DC为轴的圆锥，在两个圆锥上各任意取一条母线，这两条母线(大多是异面直线关系)所成的角就是题意所求。根据异面直线所成角的定义，只能改变(平移)圆锥的位置求解。尝试把以DC为轴的圆锥平移，并进行反向延长，得图4。当两母线分别是BA1，BM1的时候，所求的夹角为70°，为最大。

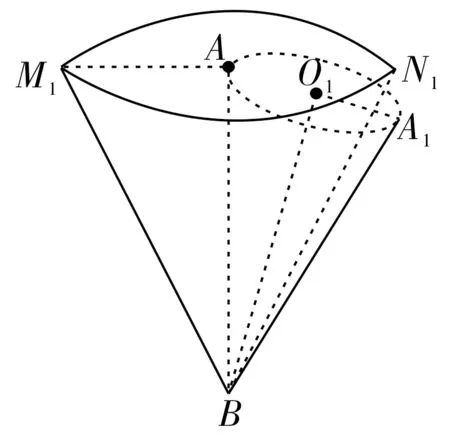
图4

进一步问：当直线AB与直线DF在什么情况下所成角最小呢?

图5

解：如图5，建立空间直角坐标系，不妨设正方形的边长为1。在圆C上任意取一点P，由，得，在圆O1上任意取一点Q(x，y，z)，其中P，Q是两个相互独立的运动点。分析Q点，Q点可由|BQ|=1和来确定，其中，O1(cos20°sin20°，0，cos220°)，所以Q点 是由方程组确定的。

由0°≤α≤40°，显然有；又由t的独立性，要使等号成立，需要；显然当α=40°且sin(t+β)=1 时，式子达到最小值，即，即θ取到最大值70°；当α=40°时，由Q点满足的方程组可得z=cos40°，x=sin40°，y=0，从而有β=90°，t=0°，即Q点与A1点重合，P点与N点重合。又在中，令sin(t+β)=-1，则cosθ=sin(α+60°)，取α=30°，可得cosθ的最大值为1，即θ取到最小值0°。此时z=1+cos30°，x=2tan 70° sin215°，y=。再求β的值。然后由sin(t+β)=-1可求得t的值，即证明了“θ取到最小值0°”的确定(存在)性，这就验证了两个圆锥面的公共部分应该是直线(公共母线)。

综上可知，直线AB与直线DF所成角的范围为0°～70°。

评注：求解空间动态问题，建立合适的空间直角坐标系，将动态问题转化为向量问题，可以获得事半功倍的效果。