燃油箱耗氧惰化与中空膜惰化的数值模拟及比较
2020-06-16王苏明冯诗愚李宗祺彭孝天刘卫华
王苏明,冯诗愚,李宗祺,彭孝天,刘卫华
(南京航空航天大学 航空学院 飞行器环境控制与生命保障工业和信息化部重点实验室,南京210016)
飞机燃油系统的起火或爆炸是造成各类军机民机失事的主要原因之一[1-2]。自1996年7月环球航空公司TWA800飞机飞行事故以来,燃油箱的安全性受到了国内外高度重视[3]。
机载惰化技术中,由于Halon1301的热稳定性和化学惰性,Halon1301惰化技术应用于F-16、F-20等飞机中[4]。但是Halon1301对环境有很大破坏,随后发展的采用中空纤维膜制取富氮气体的机载惰化气体产生系统(On-Board Inert Gas Generation System,OBIGGS)由于经济实用的特点应用于F-15、F-22、F-35等飞机中,其富氮气体(Nitrogen Enriched Air,NEA)的氮含量通常在88% ~98%之间[5-6]。只要保证燃油箱气相空间的氧浓度低于极限氧浓度(Lim itation Oxygen Concentration,LOC),则能保证燃油箱被惰化。但是,OBIGGS存在对气源压力要求高、分离膜容易被污染等缺点[7-8]。
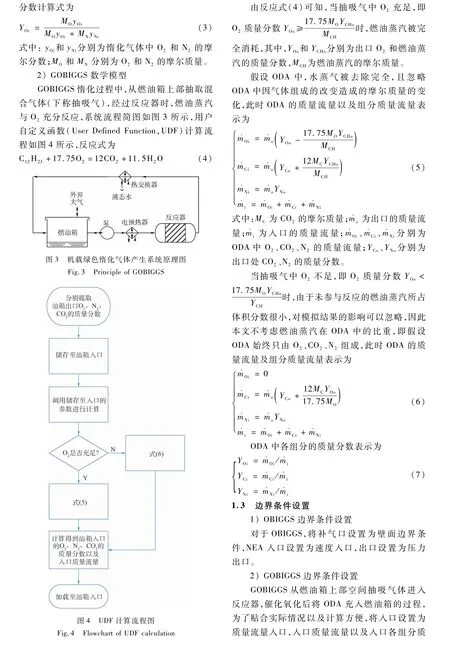
近年来,美国提出了新一代机载惰化技术——耗氧型惰化系统,即机载绿色惰化气体产生系统(Green On-Board Inert Gas Generation System,GOBIGGS),其基本原理是:从燃油箱上部空间提取空气和燃油蒸汽,通过催化氧化反应器进行可控的催化反应,其反应器出口的惰化气体为CO2、N2和少量未反应的O2,称为缺氧空气(Oxygen Depelated Air,ODA)。从国外文献报道来看,由于无需从发动机引气,其代偿损失小,同时相比OBIGGS,其拥有更高的惰化效率[9-11]。
目前国内对燃油箱惰化技术研究主要集中在中空膜惰化和燃油洗涤惰化方面[12-14],对GOBIGGS技术的研究起步较晚,目前还只停留在国外资料消化和前期的系统仿真阶段,例如冯诗愚等[15]在进行了大量简化的前提下,采用集中参数法对其进行了0维瞬态仿真,分析了反应器效率对惰化性能的影响。但是NEA和ODA气体组成成分存在差异,特别是ODA中含有CO2,其密度远大于N2和O2,因此2种气体充入燃油箱后浓度的分布和流动状态必然存在差异。有鉴于此,本文采用CFD方法对OBIGGS和GOBIGGS两种系统进行模拟,得到燃油箱上部空间各组分流动情况,并与燃油箱中空膜技术的惰化效率进行比较,为中国的新一代机载惰化技术研究工作提供支持。
1 计算方法与数学模型的建立
本文对OBIGGS与GOBIGGS惰化过程分别建立了数学模型,并采用Fluent模拟软件进行模拟,选取Jet A燃油作为研究对象,其分子式可以简化为C12H23,现作出如下假设:
1)燃油箱内气体视为理想气体。
2)计算步长内,各种气体充分混合。
3)在指定温度下,燃油箱内燃油蒸汽的体积分数保持不变。
4)2种模型下,恢复平衡状态所需的弛豫时间远小于时间步长Δt。
5)GOBIGGS模型下,反应器内燃油蒸汽与O2充分反应,且水蒸气去除完全。
1.1 几何模型与数值计算方法
对2种系统模拟采用相同的燃油箱模型,燃油箱为立方体结构,带有气体入口、出口和补气口(见图1),燃油箱容积为2.5m3,长宽高如图所示,入口、出口以及补气口面积均为9.4×10-3m2,为了防止补气口可能出现的回流,增加一个高度为0.15m的补气管道,区别在于对OBIGGS进行模拟时,将补气口设置为壁面边界条件,即OBIGGS不存在补气口。
本文采用ICEM CFD对燃油箱进行网格划分,为了提高网格精度,采用结构化网格,划分网格如图2所示,对孔口位置进行加密,最小网格尺度为2 cm。
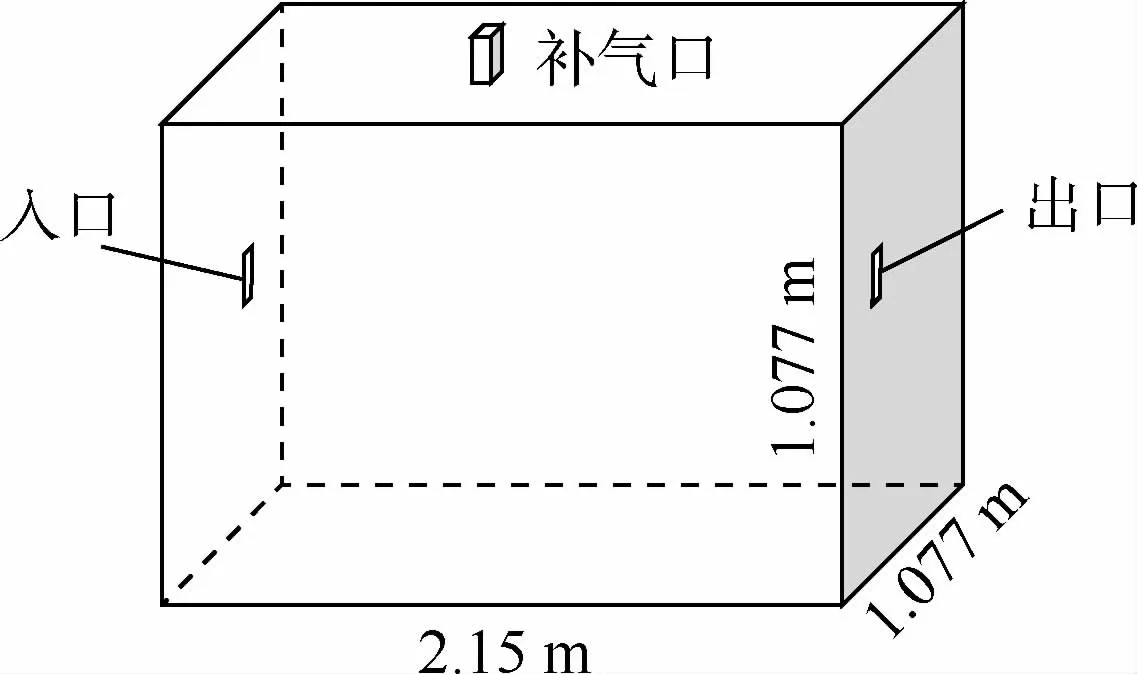
图1 几何模型Fig.1 Geometry model

图2 网格划分Fig.2 Mesh generation
采用Fluent19.0进行计算模拟,2种模拟方式速度压力耦合均采用压力隐式算子分割(Pressure Implicitwith Splitting of Operators,PISO)算法,并采用相同的控制方程,对于NEA和ODA的流动问题除遵循Navier-Stokes方程组外,同时由于计算域内组分在质量浓度梯度驱动下由高浓度区域向低浓度区域的扩散,因此还需要求解组分输运方程。由于整个过程没有发生任何化学反应,组分输运方程不考虑化学反应的净生成率以及自定义源项产生的额外生成速率。因此,控制方程主要由质量守恒方程、动量守恒方程、能量守恒方程以及组分输运方程组成,即

式中:Δ为数学符号,表示矢量的微分;ui为xi方向速度;fi为自定义动量源项;k为热传导系数;p为压力;cp为定压比热容;ST为自定义热源项;V为速度;ρ为密度;ν为运动学黏度;T为温度;Yn为组分n的组分质量分数;Jn为组分n的扩散通量;对于OBIGGS,n=1,2分别表示O2和N2;对于GOBIGGS,n=1,2,3,4分 别 表 示O2、N2、CO2、H2O。
经计算入口雷诺数Re=680,因此采用层流模型,对于层流:

式中:Dn,m为组分n的扩散系数。
1.2 2种系统数学模型的建立
1)OBIGGS数学模型
OBIGGS将一定体积流量一定氧浓度的NEA从入口充入燃油箱与燃油箱内气体混合后从出口排出,从而对燃油箱进行惰化,入口处O2的质量

2 燃油箱数值模拟结果验证与分析
2.1 燃油箱中空膜数值模拟结果验证
为验证本文建立的数值模拟方法的正确性,将模拟计算结果与文献[16]的实验数据进行比较,采用NEA4进行中空膜惰化,NEA体积流量分别为56.6、111.2、152.9 L/min,燃油箱内初始O2摩尔分数为0.21。
图5为燃油箱气相空间O2摩尔分数随时间的变化关系。从图中可以看出,惰化进行至1 600 s,体积流量为56.6 L/min时,利用CFD技术的数值模拟结果与实验结果吻合得较好。随着体积流量增大,数值模拟结果与实验结果的差距也在增大。惰化进行至1 600 s,体积流量为152.9 L/min时,数值模拟结果与实验结果显示的燃油箱内O2摩尔分数分别为0.075和0.07,相差6.7%。本文主要对比GOBIGGS与OBIGGS两种系统的惰化原理与惰化性能的差异,数值模拟结果与实验结果的误差在可接受的范围内,这证明了本文体积模拟方法的准确性和可行性。
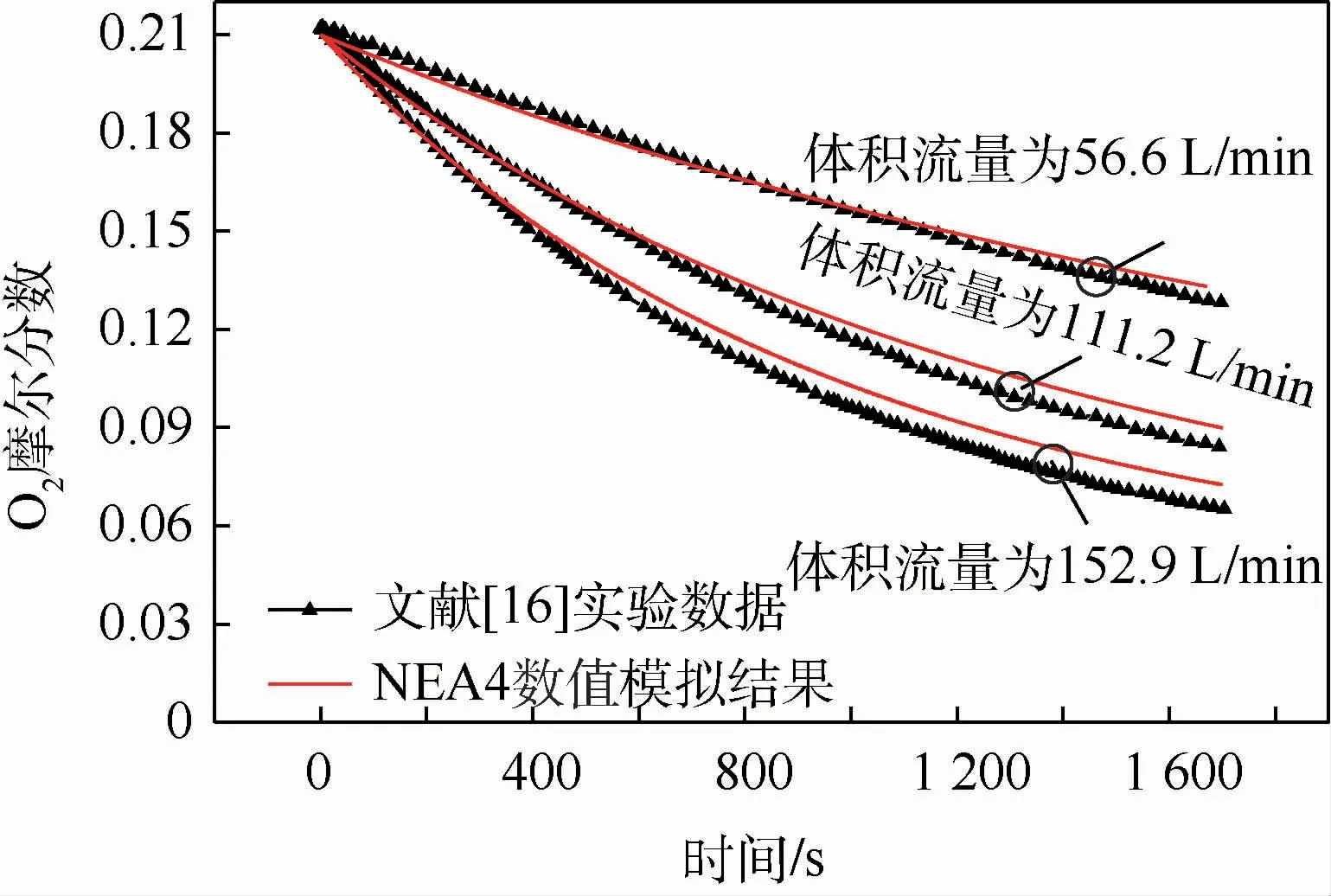
图5 数值模拟结果与文献[16]实验数据对比Fig.5 Comparison of numerical simulation results with experimental data of Ref.[16]
2.2 OBIGGS和GOBIGGS数值模拟结果
将GOBIGGS的出口的抽吸气体积流量设置为111.2 L/min,根据文献[17],40℃时,燃油箱上部空间的燃油蒸汽的体积分数为0.8%。入口体积流量与入口组分质量分数通过UDF加载至Fluent,得到GOBIGGS的燃油箱上部空间O2摩尔分数随时间的变化关系,同时计算出相同体积流量下NEA0的OBIGGS的燃油箱上部空间O2摩尔分数随时间的变化关系,如图6所示,对于GOBIGGS燃油箱入口和出口中O2与CO2的质量分数随时间的变化关系,如图7所示。
从图6和图7中可以看出,GOBIGGS惰化阶段分为2个阶段:第1阶段,开始到660 s时O2充足,ODA中O2的质量分数快速降低,CO2的质量分数逐渐增加,燃油箱内部O2摩尔分数下降速度逐渐增大;第2阶段,660 s以后O2不足,此后ODA中O2的质量分数持续为0,CO2的质量分数趋于稳定,忽略ODA中的燃油蒸汽,此时ODA中只有N2和CO2,燃油箱上部空间O2摩尔分数随时间变化关系趋于NEA0时OBIGGS燃油箱上部空间O2摩尔分数随时间变化关系。
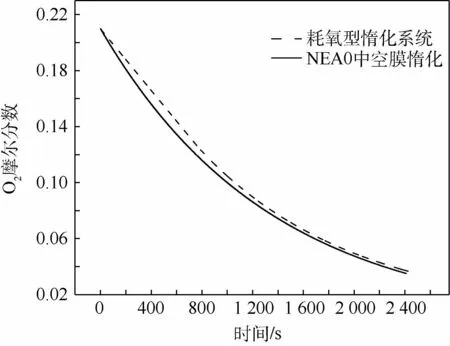
图6 不同模型下O2 摩尔分数随时间变化关系比较Fig.6 Comparison of oxygen mole fraction variation with time under differentmodels
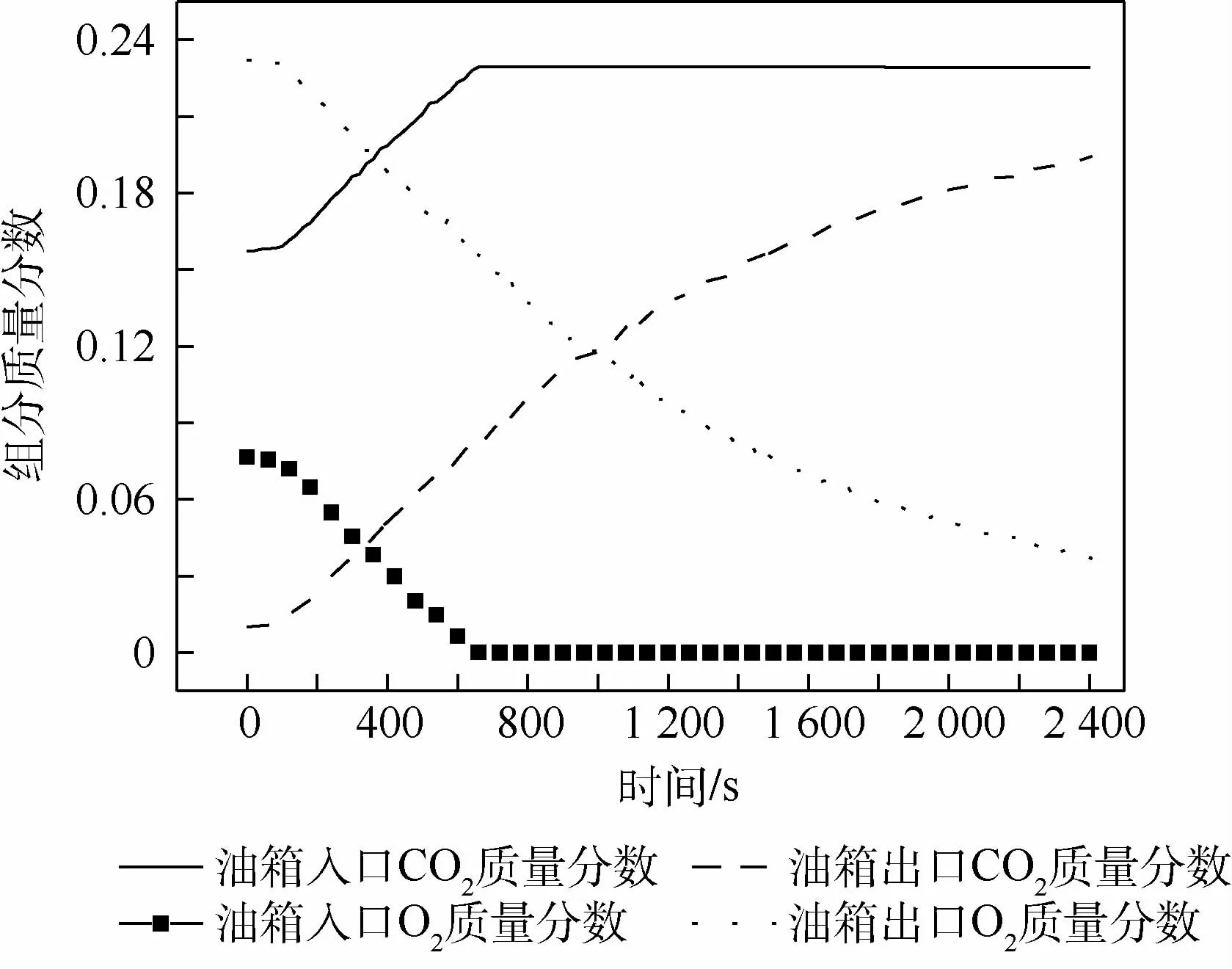
图7 GOBIGGS燃油箱入口O2 和CO2 质量分数随时间变化关系Fig.7 Time-dependent oxygen and carbon dioxide mass fractin at fuel tank inlet of GOBIGGS
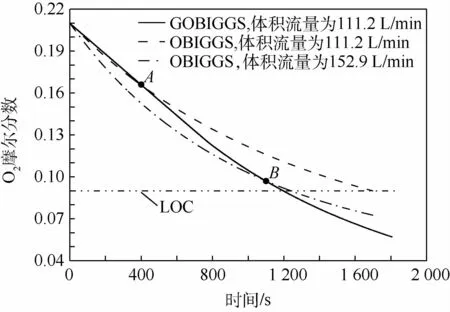
图8 不同体积流量、不同模型下O2 摩尔分数随时间变化关系比较Fig.8 Comparison of oxygen mole fraction variation with time under different volume flow rates and differentmodels
图8将体积流量分别为111.2 L/m in和152.9 L/min的OBIGGS与体积流量为111.2 L/min的GOBIGGS燃油箱上部空间O2摩尔分数随时间的变化关系进行了对比。从图中可以看出,在相同体积流量下,第1阶段,由于ODA中O2摩尔分数在前期一段时间内高于NEA4的OBIGGS的惰化气体中O2摩尔分数,GOBIGGS的燃油箱上部空间O2摩尔分数略高于OBIGGS,但随着GOBIGGS惰化气体中O2摩尔分数持续下降,GOBIGGS的燃油箱上部空间O2摩尔分数的下降速度迅速增大,3种计算条件O2摩尔分数达到9%所需时间从小到大依次为1 196、1 238、1 697 s,可以看到,相同体积流量下,GOBIGGS的惰化效果远好于NEA4的OBIGGS,且体积流量为111.2 L/min的GOBIGGS的惰化时间小于体积流量为152.9 L/min的NEA4的OBIGGS的惰化时间。
2.3 OBIGGS和GOBIGGS的O 2 摩尔分数分布
图9给出了图8中2个交点A、B处的流场分布图。图9(a)为在400 s时,体积流量均为111.2 L/min的GOBIGGS和OBIGGS的流场分布图;图9(b)为在1 100 s时,体积流量分别为111.2 L/min和 152.9 L/m in 的 GOBIGGS 和OBIGGS的流场分布图。
从图9可以看到,在燃油箱内平均O2摩尔分数相同的情况下,两者O2摩尔分数分布存在显著差别。对于GOBIGGS,上部空间O2摩尔分数明显大于下部空间,OBIGGS则相反,主要原因在于NEA中主要气体为N2,其密度低于O2,故此会浮在O2上方,而ODA中含有约20%的CO2,其密度远大于O2,因此会向下沉积。显然当燃油箱存在燃油时,气相空间的O2摩尔分数也与此类似。
在两者平均O2摩尔分数相同,且均小于LOC的情况下,GOBIGGS的安全性优于OBIGGS,其原因在于CO2的覆盖作用,气-油界面燃油蒸汽最高的区域被保护,一旦燃油箱其他局部位置产生燃烧,在CO2的保护下燃烧不易向气-油界面扩散而加剧燃烧,反而有可能抑制燃烧,OBIGGS则相反。
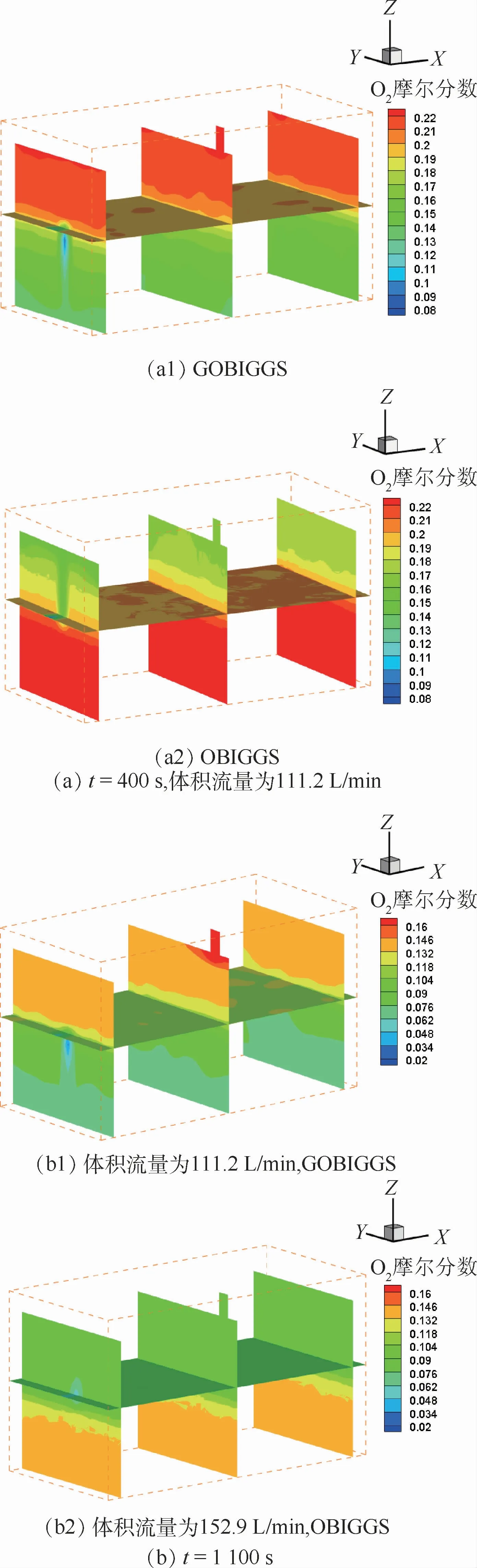
图9 不同模型的O2 摩尔分数分布云图Fig.9 Oxygen mole fraction distribution contours of differentmodels
3 结 论
本文建立了GOBIGGS和OBIGGS的数学模型,并分别模拟了GOBIGGS与OBIGGS的流场分布,OBIGGS数值模拟结果与实验结果相比较显示数值模拟结果较为准确,研究结果表明:
1)GOBIGGS惰化过程分为2个阶段:第1阶段,O2充足时,ODA中O2的质量分数快速降低;第2阶段,O2不足时,ODA中O2的质量分数持续为0,此时GOBIGGS使燃油箱气相空间O2摩尔分数下降曲线与100%NEA的OBIGGS使燃油箱气相空间O2体积分数下降曲线相近。
2)相同惰化气体体积流量下,GOBIGGS使燃油箱气相空间O2摩尔分数达到LOC所需时间远小于OBIGGS;在ODA流量体积为NEA的一半时,GOBIGGS使燃油箱气相空间O2摩尔分数达到LOC所需时间仍略小于OBIGGS,主要原因在于ODA中O2含量极低。
3)GOBIGGS对燃油箱进行惰化时,气相空间上部O2摩尔分数大于下部空间O2摩尔分数,OBIGGS则相反,主要原因在于NEA中主要成分为N2,密度小于O2,浮在O2上方,ODA中含有20%左右的CO2,密度大于O2,沉在O2下方。
