热化学反应方程式教学过程中的反思

朱晓珍

【摘要】化学反应过程中同时存在着物质与能量的变化，而热化学方程式正好体现出这两者之间的关系，这对于燃料燃烧所放出的能量、热工和化工等各方面都有重要的意义。本文首先阐述了热化学方程式的书写要求，再结合自己在教学过程中的一些思考，谈一谈如何更好的掌握热化学方程式。

【关键词】热化学方程式;反应热大小;计算反思

一、热化学方程式对比普通化学方程式

1.热化学方程式的特点

热化学方程式就是化学方程式的一种，它包含两个方面，一个是物质变化，一个是能量变化。即参加反应的物质的量与反应热的关系的一种式子。通过与普通的化学方程式相比，它有以下几点的不同：1.反应物、生成物的状态;2.反应条件只表示温度与压强，大多数的反应热是在298K、101kPa下测定的，可不注明反应条件。不用注明气体或沉淀符号等;3.要根据化学计量数写出相应的反应热的数值。放热反应即放出能量（热量），热量与反应热成负相关关系，反应热为负值;吸热反应即吸收能量（热量），热量与反应热成正相关关系，其反应热为正值;4.配平后的化学方程式中，各物质的化学计量数仅表示物质的量，不表示分子或原子的个数，故可以是整数，也可以是分数;5.反应热△H与参加反应的物质的量有关，化学计量数加倍，△H也要相应加倍;6.反应热的数值与物质的量要成正比。

2.巧记热化学方程式

听到这里很多同学就混乱了，内容太多，记不住。这时我们可以对这些信息进行处理，站在学生的角度，用更精炼的语言去概括小结。我们可以把以上信息归纳为3点：第一个是看反应热，第二个是看物质的状态，第三个是看反应条件，只要记住了这三点，相信学生们可以正确快速的判断热化学反应方程式的正误，写对热化学反应方程式。例如，1molA气体和1mol的B气体恰好反应生成1mol的E气体和3mol的F气体，吸收 w kJ热量，写出该热化学方程式？同学们可以利用上述三点快速得出答案：A（g）+B（g）=E（g）+3F（g）;△H = + w kJ/mol 。

3.注意特殊要求

在书写热化学方程式时，还要区分普通的热化学方程式、中和热的热化学方程式以及燃烧热的热化学方程式。有限定条件的按限定条件来书写，否则普通的热化学方程式的书写因系数的不同可以出现多种答案。例如，稀溶液中，1mol的硫酸溶液与KOH完全反应时，放出114.6kJ热量，写出表示中和热的化学方程式？根据特殊要求，中和热的热化学方程式中生成物H2O（l）的化学计量数必须是1，答案为1/2 H2SO4（aq）+KOH（aq）=1/2 K2SO4（aq）+H2O（l） ;△H = -57.3kJ/mol 。

二、反应热大小比较

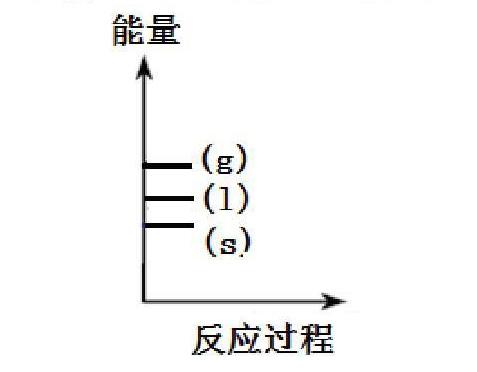
反应热大小比较可以利用技巧来巧记。例如，①C（s）+O2（g）=CO2（g） △H1 ; ②C（s）+1/2O2（g）=CO（g）△H2 ，比较△H1与△H2的大小？我的方法是，先判断该反应是放热反应还是吸热反应，如果是放热反应，热效应与△H成反比，热效应越大，△H值就越小。如果是吸热反应，热效应与△H成正比，热效应越大，△H值也越大。式①式②都是放热反应，式①是完全燃烧，热效应比较大，则△H1就比较小;式②是部分燃烧，热效应比较小，则△H2就比较大。还有一种状态比较法，可以利用作图的方法，更直观的得出正确答案。同种物质的三种不同状态的能量图如下：

三、关于反应热简单计算的反思

关于反应热的计算是难点内容，主要有两种表达式：（1）△H等于反应物断键吸收的能量减去生成物成键释放的能量，用通俗的语言来概括就是按顺序从左边减去右边。（2）△H等于生成物的总能量减去反应物的总能量。这个学生比较好理解，通常以图表的形式考查，形象直观，可以直接判断该反应的能量变化。旧化学键的断裂和新化学键的形成，是从微观的角度去探析;与周围环境之间存在的热量交换，是从宏观的角度去辨识，两者之间相互作用而导致对环境的影响，就是要学生们形成从宏观和微观相结合的角度去分析和解决实际问题的能力。

我们在运用盖斯定律去计算反应热时，许多老师容易犯的一个误区是：我们自认为很简单的相加减数学问题，在课堂上会轻易的一笔带过，直接说出式①加上式②等于目标方程式。回想一下，自己在刚刚走上讲台教书的那年，遇到这样的計算题，都要在草稿纸上演算一遍，写出详细的计算过程，生怕算错，谨慎对待，更何况是现在的学生，他们也更需要这样的一个演算过程。留出点时间，让学生们自己动手写一写，更能加深他们的印象，记忆更深刻。

以上是笔者在教学过程中对热化学方程式的见解与反思，作为一线教师，只有在平时的工作中不断反思，不断总结，更多地从学生的角度出发，把复杂的问题简单化，把简单的问题具体化，用通俗易懂的语言概况总结，用生动形象的语言打动学生，让更多的学生能轻松地投入到化学学习中来。

参考文献：

[1]曲一线.同学教材分层讲练·高中化学·化学反应原理：人教版[M].北京：教育科学出版社，2018（3）：3-8.

[2]任志鸿.高中优秀教案[M].南方出版社，2005（8）：66-78.