基于城市供水管网优化调度研究

叶 露 ，郑雪婷

（沈阳建筑大学 市政与环境工程学院，辽宁 沈阳 110168）

随着城市的快速发展和日益紧张的水资源开发，城市供水管网传统的经验调度形式已无法满足当代科学化管理管网的要求，以计算机技术和数学模型作为基础的管网优化调度模型是管理供水管网的重要技术手段。在水质、水量以及水压等基础上，通过建立模型达到节水和节省费用的目的，以提供科学化的供水管网管理模式。Chase等[1]采用非线性规划算法求解目标函数，并用水力模拟解决管网约束问题，得到较准确的结果，但是对大规模管网，采用该算法的计算效率显著下降，甚至出现无解的情况。Pasha 等[2]提出了泵组能耗-流量的线性规划模型，通过计算可最快速地求出最优解，为大型管网计算提供了便利条件。信昆仑等[3]基于综合水龄指数建立管网水力优化调度模型，采用遗传算法实现优化问题求解，优化效果较好。牟天蔚等[4]通过引入漏失量与电耗之和作为目标函数，提出布谷鸟算法对泵组实时调度模型的研究，结果表明节能效果较好。

城市供水管网建立的水力学模型越复杂，其模型算法计算量也就越大，建立模型通常采用最优算法得出最优解。本篇论文在前人研究的基础上，采用遗传算法来对管网分别进行一级、二级优化计算，建立模型进行优化调度研究。

1 优化调度模型的建立

1.1一级优化调度的目标函数及约束条件

管网经济性目标通过控制管网的供水费用来实现，可靠性目标通过减小管网压力实现。根据目标函数建立管网模型，通过合理分配各水厂、泵站的供水量最终确定出系统内水泵最优流量和扬程，从而能达到系统的整体优化[5]。

1.1.1 目标函数

将水厂运行时产生的总费用作为经济目标以及水厂供水管网的压力来作为目标函数。

（1）制水成本f1：

式中：Qi——第i个水厂的供水量（m3/h）；

C1i——第i个水厂单位水量制水成本(元)；

N——水厂个数。

（2）泵站运行费用f2：

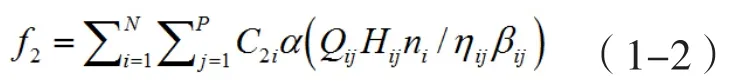
式中：

Qij——单泵供水量（m3/h）；

Hij——单泵扬程（m）；

ni——水泵运转数（台）；

ηij——水泵效率；

βij——水泵电机效率；

C2i——耗电成本；

P——水泵数；

α——耗电系数。

（3）供水收入f3：

式中：Qi——水厂的供水量（m3/h）;

C3i——水厂单位水量售价（元）；

N——水厂数。

则运行目标函数为：

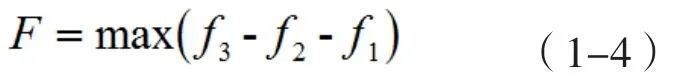
1.1.2 约束条件

城市供水管网优化调度的约束条件主要包含以下几方面[6-8]：

（1）供水量约束

式中：Qi——泵站的供水量（m3/h）；

Qimin——泵站的最小供水量（m3/h）；

Qimax—— 泵站的最大供水量（m3/h）。

（2）供水压力约束：

式中：Hi——供水压力，m；

Himin——最小供水压力（m）；

Himax——最大供水压力（m）。

（3）管网水力平衡约束：

式中：m——泵站个数；

Qt——管网需水量（m3/h）。

（4）监测点水压约束：

式中：hj——第j个测压点的服务水头（m）；

hjmin——第j个测压点的最低运行水头（m）；

hjmax——第j个测压点的最高限制水压（m）。

（5）水泵转速约束：

式中：nij——i泵站j水泵的转速(r/min)；

nijmin——i泵站j水泵的最低转速(r/min)；

nijmax——i泵站j水泵的最高转速(r/min)。

1.2 二级优化调度的目标函数及约束条件

供水管网建立二级优化调度模型的目标函数一般情况下是泵站整体运行时的功率，水泵的转速比和开启度作为决策变量，供水系统的运行状态和水泵机组的供水能力通常是作为约束条件。在供水量一定的情况下，供水管网运行功率最小时，供水设备的转速情况以及组合的方式，从而达到供水系统的优化和节能。

以陕西办事处、南阳办事处、邯郸办事处、胶东办事处、豫东办事处、晋南办事处、福建办事处，广西办事处、四川办事处、山西省社会化服务体系为根据地，打造的十大现代农业技术服务的探索基地和价值营销的实践基地，形成了天脊品牌提升的重要基点和“市场堡垒”。

1.2.1 目标函数

（1）定速泵功率：

（2）调速泵功率：

式中： Qi——第i台水泵流量；

si——第i台水泵流量转速比；

Wi——水泵开启决策变量；Wi=0，水泵未投入运行；Wi=1，水泵投入运行。

l——定速泵台数；

a0i，a1i，a2i——第i台水泵流量功率曲

线拟合参数。

1.2.2 约束条件

（1）转速比约束：使调速泵运行时在高效区域工作。

式中：Simn，Simax——水泵转速比的最小值和最大值。

（2）总流量约束：

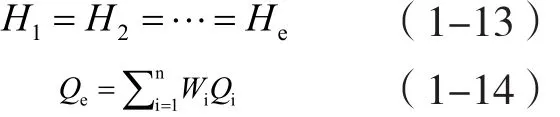
式中：He——一级优化调度中求得的泵站最佳供水压力；

Qe——一级优化调度中求得的泵站最佳供水量。

（3）单泵流量约束：

式中：Qimin，Qimax——水泵供水量的最小值和最大值。

1.3 建立数学模型

供水管网优化模型建立的最终目的就是将多目标因素转化为单目标因素进行求解，以目标函数及其约束条件为基础建立管网数学模型，采用最优算法求出最优结果。

则一级优化调度数学模型为：

二级优化调度数学模型：

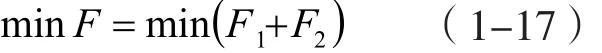
2 遗传算法求解优化调度模型

遗传算法在1975 年由美国的J.Holland教授提出，正式兴起于20世纪90年代，因其效率高、适应性好等优点而被广泛应用。自然界生物中每个表现型都对应一对基因，人们受生物种群内基因的选择、变异、重组等遗传操作启发创造了寻优算法[9-10]。遗传算法是从整个集合进行寻优，而不是以单个个体逐步迭代寻优，所以具有全局搜索能力，且可以多个个体并行寻优，避免了陷入局部最优解的风险；遗传算法具有很好的自组织性、自适应性和自学习性。因此，相较于传统的寻优算法，遗传算法具有很强的适应性，能够在所有种群中进行搜索，适合处理很多复杂的模型。但是遗传算法较于其他传统优化算法的效率低，且容易过早收敛，发生早熟现象[11]。但是由于遗传算法在对整体进行寻优计算时需要的信息相对较少，同时对函数的要求也相对较少，当对多个领域的复杂问题进行求解时只需一套求解框架即可，因此遗传算法对组合问题进行优化求解时的准确度较高，相比于其它算法，该算法的效率也相对较高。遗传算法的运算过程如图1所示：

图1 遗传算法计算流程图

3 优化调度模型实例应用

某市B水厂，有一个供水泵站，由于供水管网错综复杂等众多因素，考虑到其实用性和复杂性，采用一级和二级并用的两级优化调度来对供水管网进行科学化的管理。

3.1 一级优化调度模型的建立与求解

管网一级优化调度模型的建立是将多目标问题转化为单目标问题，将每一台水泵的供水量和水泵的供水压力来作为一级优化调度模型的决策变量，分别将供水管网运行时的经济目标及其可靠性作为目标函数。

在模型建立时为了能够更高效的节约水源，因此本篇文章在建立模型时加入了节水系数Ki。

则目标函数为：

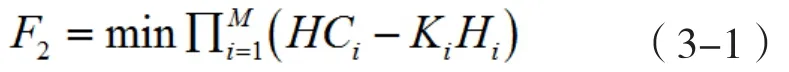
总平衡公式：

式中：K值为每个压力检测点处的节水系数Ki的加权平均值。

城市供水管网复杂，用户种类也不尽相同，所以节水系数也会有较大差距，在此次的研究工作中将没有进行特别说明的节水系数取值为0.97。所以节水工况下的数学模型为：

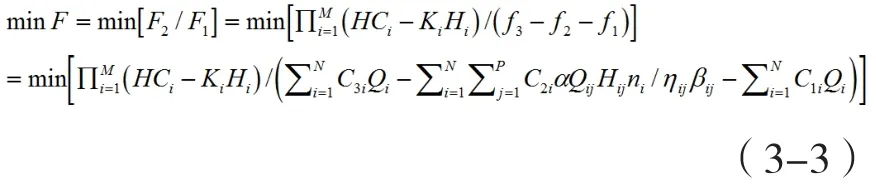
并同时结合公式（1-5）、（1-6）和公式（3-2）进行建模。已知该市B水厂的制水成本为0.15元/m3，售价为2.6元/m3，B水厂的电费为0.64元/kWh。电耗系数为0.000278[12]。

3.1.1 模型算法求解设计

采用遗传算法对优化模型进行求解，将目标函数及其约束条件进行转化，转化成采用遗传算法中所需要的条件，如染色体和遗传算子等，然后再进行编码求解。步骤如下：

（1）遗传编码

遗传编码是将优化调度中的所有变量转化成遗传算法求解过程中可以利用的能够存储一定遗传信息的遗传因子。在此次优化调度采用维数为20 的二进制编码对供水点的水量进行编码[13]。

（2）产生初始种群

初始种群是对水量进行编码后随机产生的，在本次模型中采用crtbp函数，产生的初始种群数为100，遗传代数的数值为400，其遗传代沟为0.95。

（3）评估和选择适应度值

适应度值的评估在运算的过程中是由适应度函数来加以实现的。本次模型采用费用为目标函数来作为模型的适应度函数。在评估的过程中目标函数值代入的是初始种群值，求出结果进行排序，留下最优费用目标进入下一代的遗传算法的运算中。

（4）交叉和变异操作

在遗传代数为400时的遗传变比中，设可能发生交叉的概率为0.7，变异的可能性为0.01，在这个过程中用到的函数为‘sus’、‘xovsp’等等。

3.1.2 模型求解结果分析

利用遗传算法对9月16号的预测时用水量通过建立的优化模型求解的结果进行分析，则优化前后的供水量和供水压力如表1和图2和图3所示。

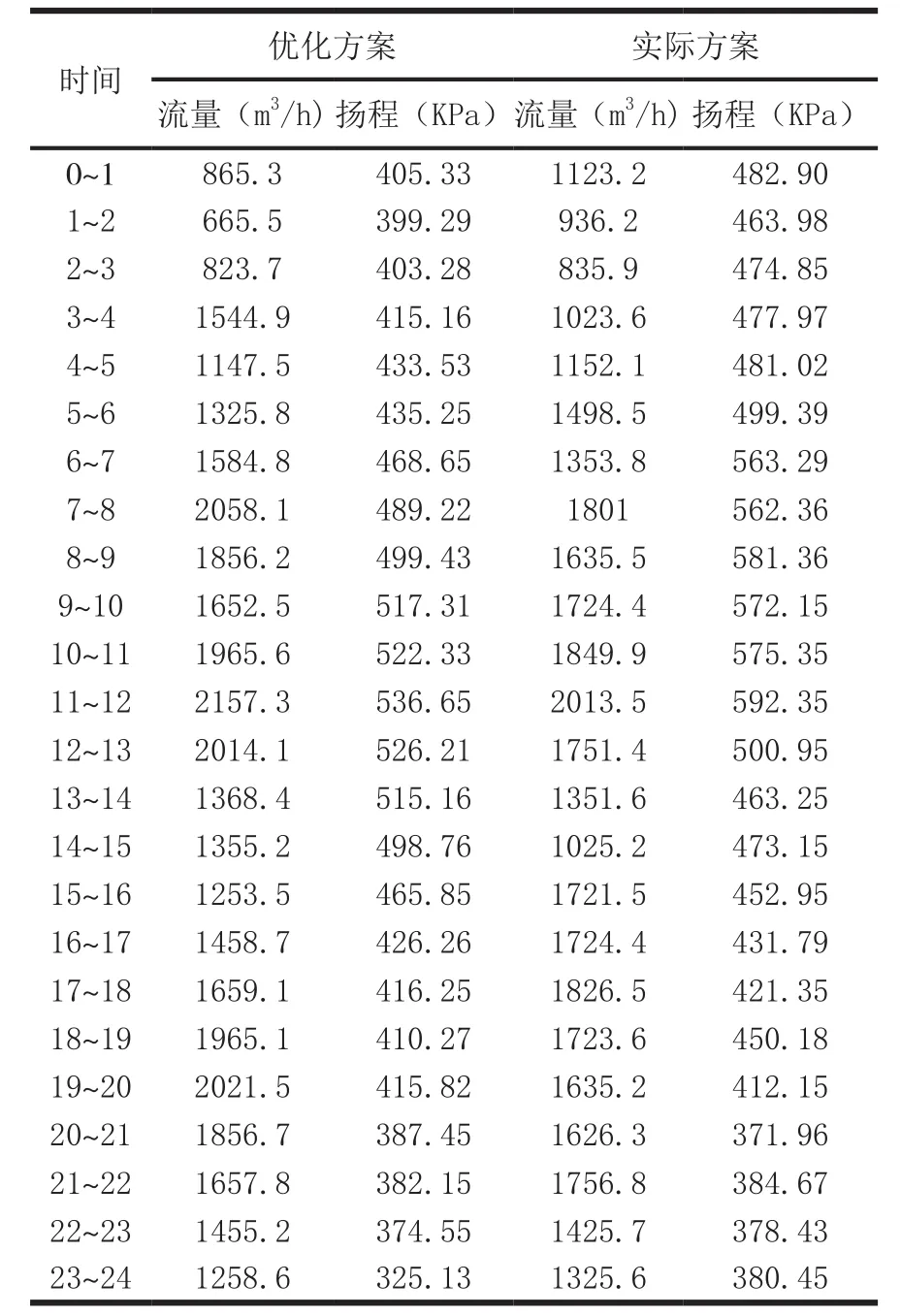
表1 B水厂优化调度方案与实际运行方案对比表

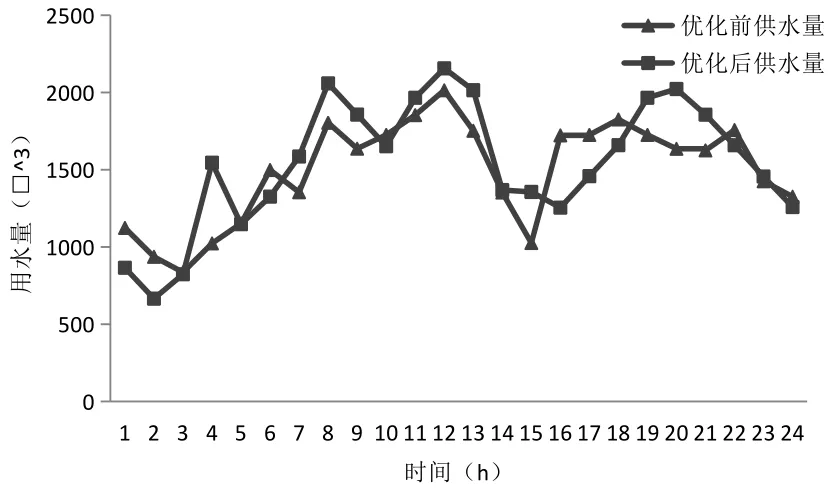
图2 B水厂供水量前后对比分析图

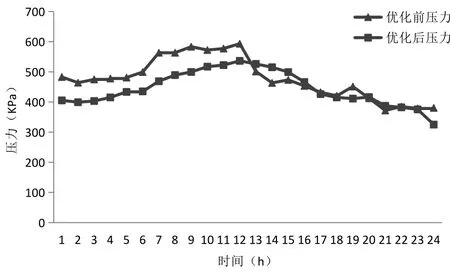
图3 B水厂前后压力分析图

根据图2可以看出供水点重新分配了供水量，由压力前后分析图3可以看出供水点处的压力值较之前有所减小，说明该方案达到了一定的可行性。

3.2 二级优化调度模型的建立与求解

3.2.1 模型的建立

在上部分的一级优化调度模型中虽然已经求出了泵站的最佳供水量和供水压力值，但是并没有对水厂中的单个泵站是如何组合做出具体分析。将水泵的运行台数和调速泵的比转速作为二级优化调度的决策变量，目标函数为单个泵站的运行功率来建立模型。B水厂的供水泵站中，定速泵为1#和5#,调速泵为2#和3#及4#水泵，B水厂的制水成本是0.15元/m3（包括水自身费用、电耗以及药耗）。

具体的数学模型为：

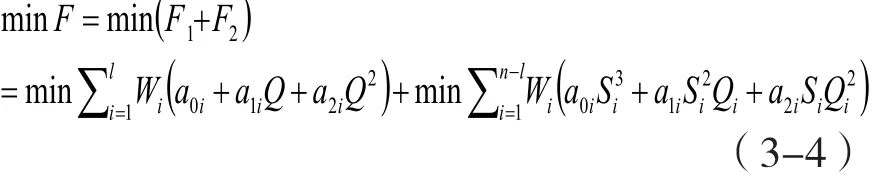
同时结合式（1-12）、（1-13）、（1-14）以及（1-15）进行二级优化调度建模。

将5台水泵的转速比作为二级优化调度的优化变量，遗传算法过程同一级优化调度相同。根据转速比公式求解出每一个水泵的流量和水厂可以提供的供水量。

3.2.2 模型结果分析

B水厂的5台水泵24h的开启情况、模型的优化结果以及优化前后的B水厂的节能情况分别如下表2、表3、表4所示：

表2 B水厂水泵开启策略表

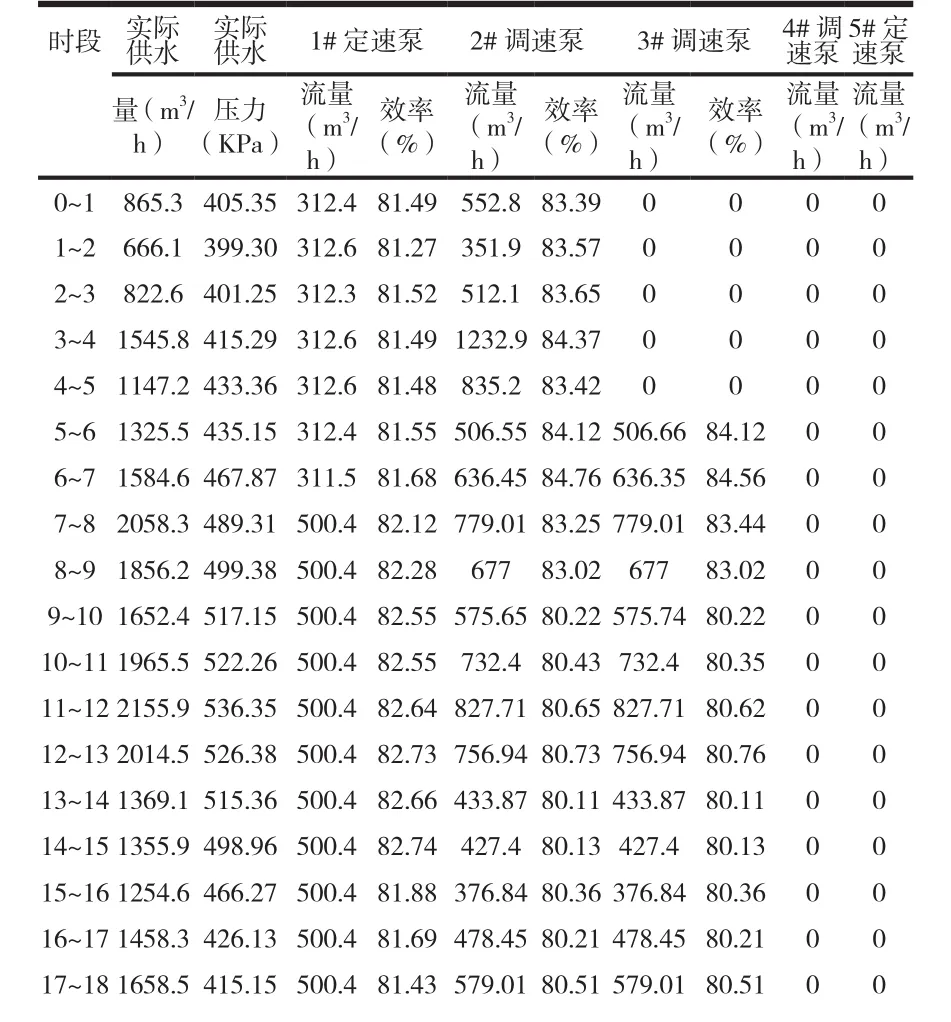
表3 B水厂泵站优化结果表

18～19 1965.6 411.28 500.4 81.55 732.4 80.33 732.4 80.33 0 0 19～20 2021.9 416.24 500.4 81.65 760.81 80.62 760.81 80.62 0 0 20～21 1856.3 387.26 500.4 81.63 677.8 80.76 677.8 80.76 0 0 21～22 1657.9 382.12 500.4 82.59 578.7 80.58 578.7 80.58 0 0 22～23 1456.4 375.57 500.4 82.41 477.8 80.66 477.8 80.66 0 0 23～24 1258.5 325.06 500.4 82.32 378.96 80.64 378.96 80.64 0 0

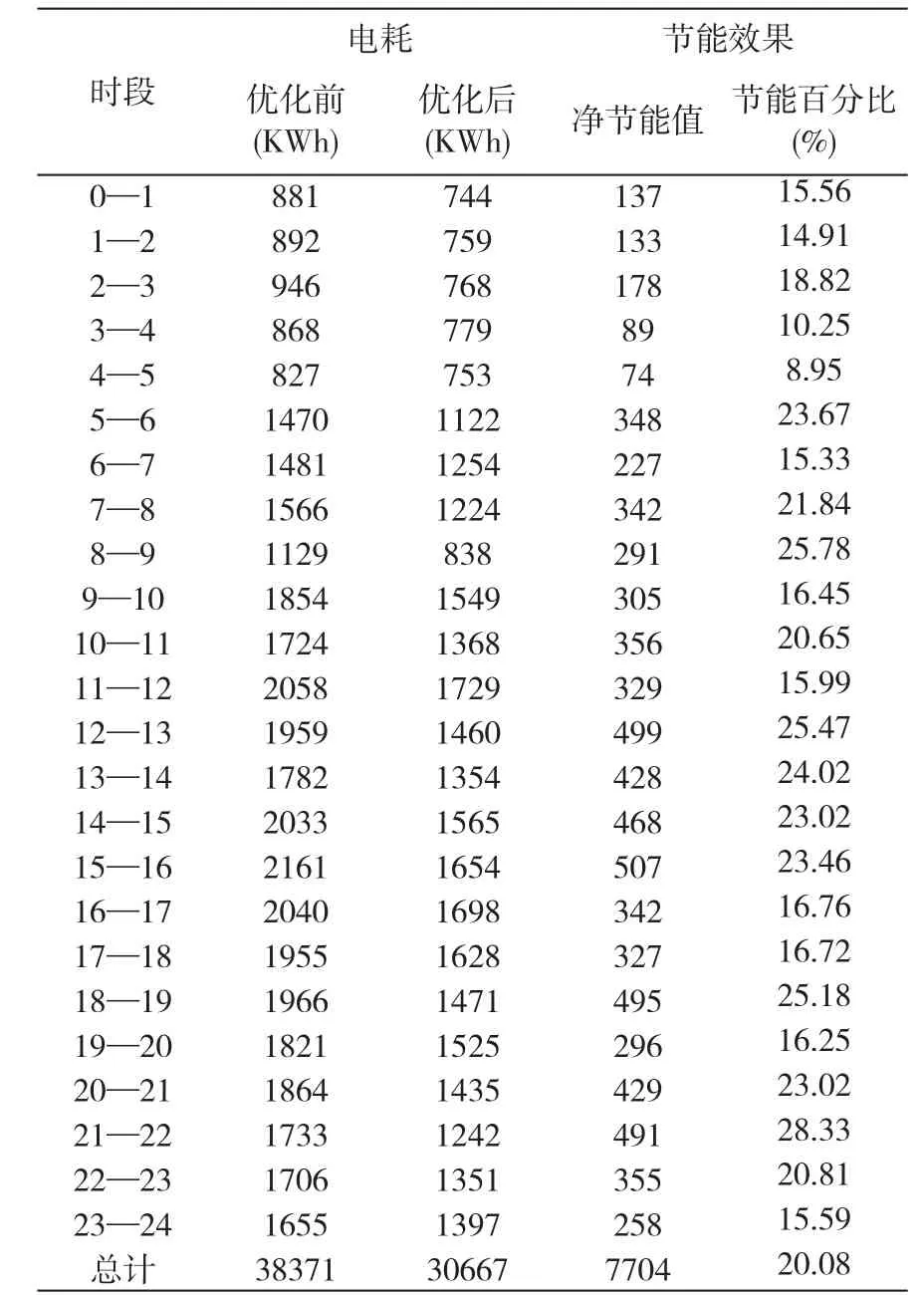
表4 B水厂优化调度前后节能分析表

根据表3可知水泵优化之后的供水量和优化之前的供水量明显不同，可以重新划分供水任务。在供水管网优化之前1#～3#水泵一直都是处于开启的状态，4#和5#为备用泵。经过二级优化模型调度后根据表3-2可知在0～5点开1#、2#水泵即可，5～24点开1#～3#水泵。优化后的泵站运行与传统经验调度相比，一天可节约电量7704kWh，节省电费大概4930.56元，优化和的节能效率可达20.08%。

4 结论

在城市供水管网水力模型优化调度的基础上，提出了通过遗传算法对某市B水厂进行一级和二级优化调度模型，实例证明一级优化调度模型求出的水压和最佳供水量，供水压力与实际监测数据相比水压较小，可以减少管网因压力过大造成管道发生爆管等事故。二级优化模型是在一级优化模型的基础上，求出泵站机组的最佳组合方式。经过优化调度后一天可节省电量7704kWh，节能效率可达到20.08%，结果表明优化后对管网具有较好的节能降耗作用，可以带来较好的经济效益。