叶轮直径对双蜗壳离心泵压力脉动特性的影响
2020-06-15杨从新
杨从新,杨 藤,刘 满
(1.兰州理工大学能源与动力工程学院, 兰州 730050; 2.甘肃省流体机械及系统重点实验室,兰州 730050)
0 引 言
离心泵是现代流体机械领域最常用的旋转叶轮机械,其叶轮部件的几何参数对流动性能的影响起着关键性作用。经过旋转部件的流体作用在静止部件上会使泵体产生振动;叶轮内发生旋转失速以及二次回流也会诱导离心泵产生振动[1-3]。为保证泵体稳定性以及降低振动产生的疲劳损坏,通过对离心泵过流部件优化以改善流致振动已成为国内外学者研究的热点[4,5]。
叶轮与蜗壳之间由动静干涉作用引起的压力脉动是离心泵振动的重要因素,其脉动幅值会随叶轮出口条件以及蜗壳条件的变化发生改变[6]。叶轮作为离心泵主要过流部件,其几何参数变化对流动性能有很大影响,合理的叶片出口安放角对优化泵内外流场起着积极作用[7,8]。不同叶轮出口宽度和叶轮直径参数直接影响着流动激励特性,故会对压力脉动频域分布有不同程度的影响[9-11]。
试验发现在小流量工况下低比转速离心泵会发生回流,且压力脉动更为明显,其表现为在轴频和叶片通过频率处会产生明显峰值[12,13]。Kergourlay等[14]采用分流叶片的方法改善叶轮周边的流动,对改善压力脉动有积极的影响。周莉等[15]对串列叶栅扩压器进行非定常流场分析,得出叶轮尾流与前排叶片尾流和缝隙流之间的相互干扰,会使脉动激励作用更加明显。倪丹等[16,17]采用LES方法对核主泵以及离心泵内部流动进行数值计算,张德胜等[18]通过对轴流泵叶轮出口尾部流动分析,均发现叶轮周期性的尾流涡是产生压力脉动的主要原因。
以上研究通过改变离心泵流动参数或叶轮几何参数分析泵内部非定常流动情况,然而对叶轮直径变化引起的叶片尾部流动状态改变与压力脉动特性的相关性研究较少;叶轮直径变化会使流道型线和叶轮与蜗壳径向间隙发生改变,进而对叶片出流尾迹结构及动静干涉效应均产生影响是影响压力脉动的重要因素;本文采用全流道六面体网格对不同叶轮直径下双蜗壳离心泵的流场进行计算[19],将外特性参数与试验数据进行对比,通过非定常计算得到各测点压力脉动信号,经过快速傅里叶变换对脉动进行频谱分析,为叶轮直径对双蜗壳离心泵内部压力脉动的影响分析提供参考。
1 计算模型与网格划分
本文以普通卧式双蜗壳离心泵(模型3)为研究对象,其基本参数为Qopt=110 m3/h,n=3 000 r/min,D2=220 mm,b2=15 mm,Z=6;以N-S控制方程为计算基础,其控制方程如式(1)~(5),考虑到其计算的不闭合性,为精确模拟流动状态,以及近壁面粗糙度对黏性流体流动的影响,结合计算资源的有限性,本文采用SSTk-ω湍流模型,SIMPLEC算法进行数值计算,该湍流模型结合了k-ω模型对近壁面计算的优点以及k-ε模型对远场计算的优点,该算法相对于其他算法更易收敛;湍动能耗散项采用二阶迎风格式,其中进口条件设置为速度入口,出口条件设置为自由出流。
(1)
其中:
(2)
(3)
(4)
(5)
式中:β*=0.09,α1=5/9,β1=3/40,σk1=0.85,σω1=0.5,α2=0.44,β2=0.082 8,σk2=1,σω2=0.856。
对离心泵进行全流道六面体网格划分,并对边界层进行加密。为了使数值计算结果更加接近试验值,考虑到除主要过流部件之外其他部分(如口环泄露等)的流动损耗,图1(a)为叶轮局部网格,图1(b)为蜗壳网格,图1(c)前口环网格图,图1(d)为后口环网格图。
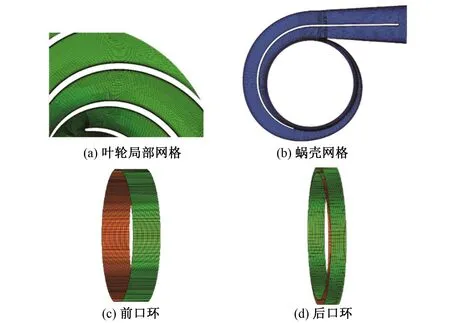
图1 计算域网格Fig.1 Computational domain grid
2 计算方法验证
经过网格无关性验证,最终选取网格总数为600万的网格,网格质量均在0.3以上;其中加密边界层的叶轮网格数为4 064 778。
对于一般离心泵叶轮,理论上叶轮直径增大前后流量、扬程、轴功率之比,等于增大前后外径1次方、2次方和3次方之比,根据单吸泵经验修正公式[20]:
(6)
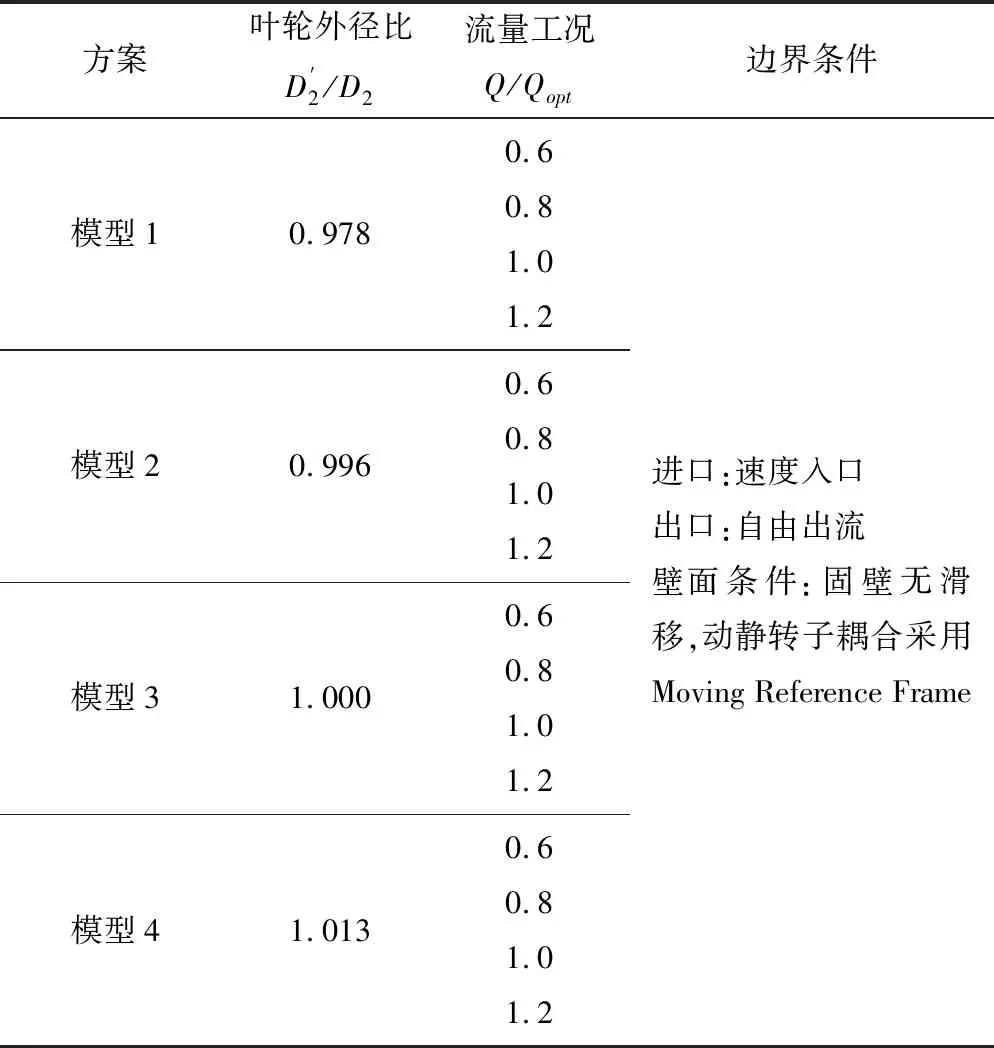
表1 计算方案Tab.1 Calculation scheme
注:Q为实际流量工况,Qopt为最优工况流量。

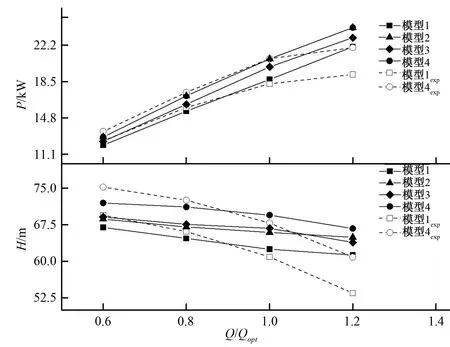
图2 模型泵特性曲线Fig.2 Model pump characteristic curve
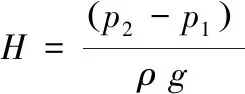
(7)
P=ρgQH
(8)
式中:H为扬程;p1、p2分别表示进出口总压;ρ表示介质密度;P表示输出功率;Q为泵的进口流量。
3 非定常计算结果分析
以定常计算结果作为非定常计算初始值。本文将时间步长设置为Δt=0.000 111 1 s,即叶轮旋转2°为一个时间步长,设置叶轮旋转5圈,取最后一圈的计算结果进行分析。在D=235 mm的基圆上设置监测点v1~v11,其中,v4~v11每点间隔45°,监测点v1位于隔舌顶圆切线与基圆相交处,v2、v3分别位于v1两侧与其夹角为10°;监测点布置如图3所示。
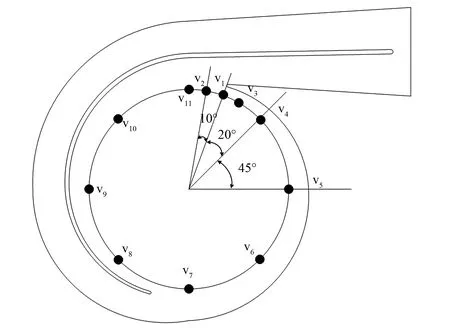
图3 监测点示意图Fig.3 Monitoring point diagram
3.1 蜗壳入口压力脉动
为了分析比较不同叶轮直径下双蜗壳离心泵的压力脉动特性,对监测点的压力值进行无量纲化,引入压力系数Cp;
(9)
(10)
式中:Δp为监测点静压值与平均静压值之差;u2为叶轮出口圆周速度。
本文研究对象的叶片通过频率(fBPF)为300 Hz。如图4,对模型3不同流量工况下隔舌区域进行快速傅里叶变换(FFT),得到频域分布,可以看出小流量工况下隔舌区域压力脉动幅值高于其他流量工况,且脉动主频出现在叶片通过频率及其高次谐波处,小流量工况受隔舌区域复杂流动影响产生回流,会产生较高峰值脉动;大流量工况下压力脉动低于额定工况和小流量工况下的压力脉动,受射流-尾迹影响,脉动峰值位于nfBPF(n=1,3)处,v2测点位于蜗壳扩散段与螺旋段交界处,此位置处会形成一个局部低压区,从而压力脉动幅值降低,但主频波动趋势与额定工况相同。结合不同流量工况下叶轮部件湍动能分布(图5)发现,小流量工况下高湍动能分布范围较大,且在叶片压力面以及叶片尾缘区域湍动能分布变化明显;但在大流量工况下,叶片压力面区域湍流脉动不明显,主要在叶片尾缘流动区发生了较强的湍动能波动。其中,湍动能系数Tu根据文献[21]定义:
(11)
式中:K表示湍动能;u2表示叶轮出口圆周速度。
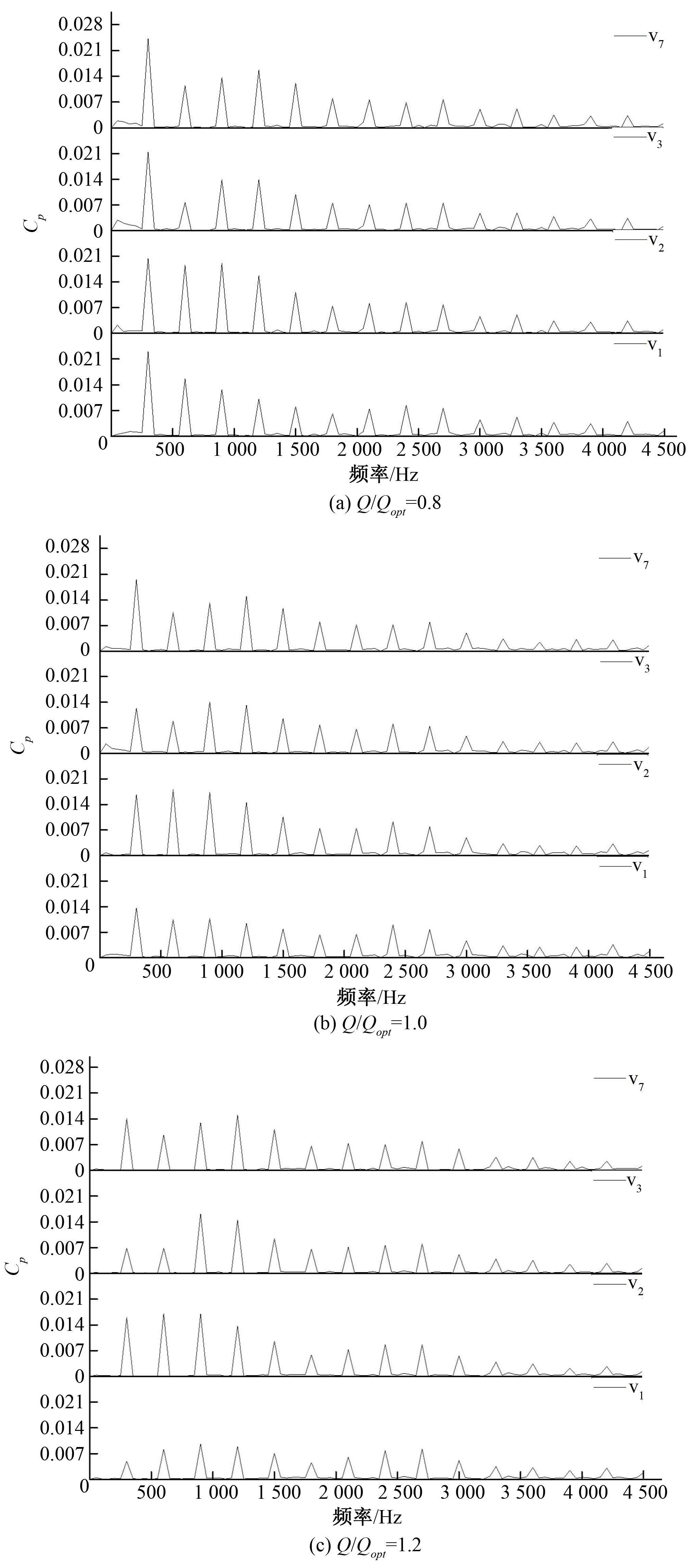
注:Q为实际流量工况,Qopt为最优工况流量。 图4 模型3各流量工况下隔舌区域压力脉动频谱Fig.4 Pressure pulsation spectrum of model 3 under various flow conditions

注:Q为实际流量工况,Qopt为最优工况流量。 图5 模型3各流量工况下湍动能分布Fig.5 Dynamic energy distribution of model 3 under various flow conditions
进一步分析不同叶轮直径下双蜗壳离心泵随叶轮周期旋转的内流场速度分布(图6),当叶片1从初始位置t0旋转至相邻叶片初始位置时,所经历周期变化为t0+2/12T,旋转角度为60°。受叶片曲率影响,叶轮旋转过程中,叶轮受到叶片做功不均匀,使得压力面受力大于吸力面,随着附面层不断增厚,流体逐渐被推向压力面,此时叶片吸力面侧容易出现流动分离现象,从而形成尾迹区;当叶片1从t0时刻旋转至t0+1/12T时刻时,叶片吸力面区域的尾流不断增厚,促进吸力侧的流体不断流向压力侧,进而形成射流-尾迹,促进了流动的混合[22];这一现象伴随着叶轮旋转至下一时刻会发生流动分离,但分离现象并不明显,叶片旋转至t0+2/12T时刻叶片尾流产生明显混合;如此周期循环,相邻叶片由于具有相同的叶片通过频率,受射流-尾迹影响会使得脉动产生叠加,如图4所示,脉动峰值出现在nfBPF(n=1,3)处,且隔舌附近的流动混合现象明显大于其他位置。这一现象可以从压力脉动时域图上看出(图7),在一个波峰和波谷中间会产生许多小的波峰和波谷,这是由幅值和频率相近的简谐波叠加形成的;一个周期内压力波动出现6个波峰和波谷,与叶轮叶片数一致,说明动静干涉是压力脉动的主要成因。
由图4中额定工况下压力脉动频谱分析发现脉动主频出现在叶片通过频率及其高次谐波处,故对不同叶轮直径下部分蜗壳周向测点频域分布(图8)进行分析,4种叶轮直径下的双蜗壳离心泵隔舌附近监测点(v11,v7)的压力脉动峰值均出现在fBPF处,远离隔舌区域的监测点受射流-尾迹影响,其脉动峰值均出现在nfBPF(n=3,4)处;除过隔舌区域监测点之外的其他监测点处压力脉动峰值处的脉动幅值随叶轮直径增大逐渐增大,且最高幅值波动达到23.8%。
3.2 隔舌区域压力脉动
图9为额定工况下不同叶轮直径下隔舌测点压力脉动频谱,分析发现除模型3以外,v2测点处压力脉动峰值出现在叶片通过频率处,且该处的脉动幅值高于其他两测点,模型1中v2与v3幅值波动最大为40.6%,v1与v3测点处压力脉动峰值出现在nfBPF(n=1,3,4)处,v2测点位于分流区,此处流体一部分进入蜗室扩散流道,一部分经隔舌撞击随叶片旋转至涡室环形流道,此处会形成复杂的流动状态,使得该位置处主频脉动为叶片通过频率;v1测点位于隔舌顶圆正下方,该处流体进入涡室环形区域,流动状态相较于v2测点更稳定,v3测点远离隔舌区域,此时主要受两叶片间射流-尾迹以及动静干涉作用导致3种叶片数的双蜗壳离心泵脉动峰值均出现在nfBPF(n=1,3,4)处。比较4种不同叶轮直径下双蜗壳离心泵隔舌区域压力脉动幅值发现模型3的压力脉动幅值明显低于其他模型,且最大波动为38.2%。
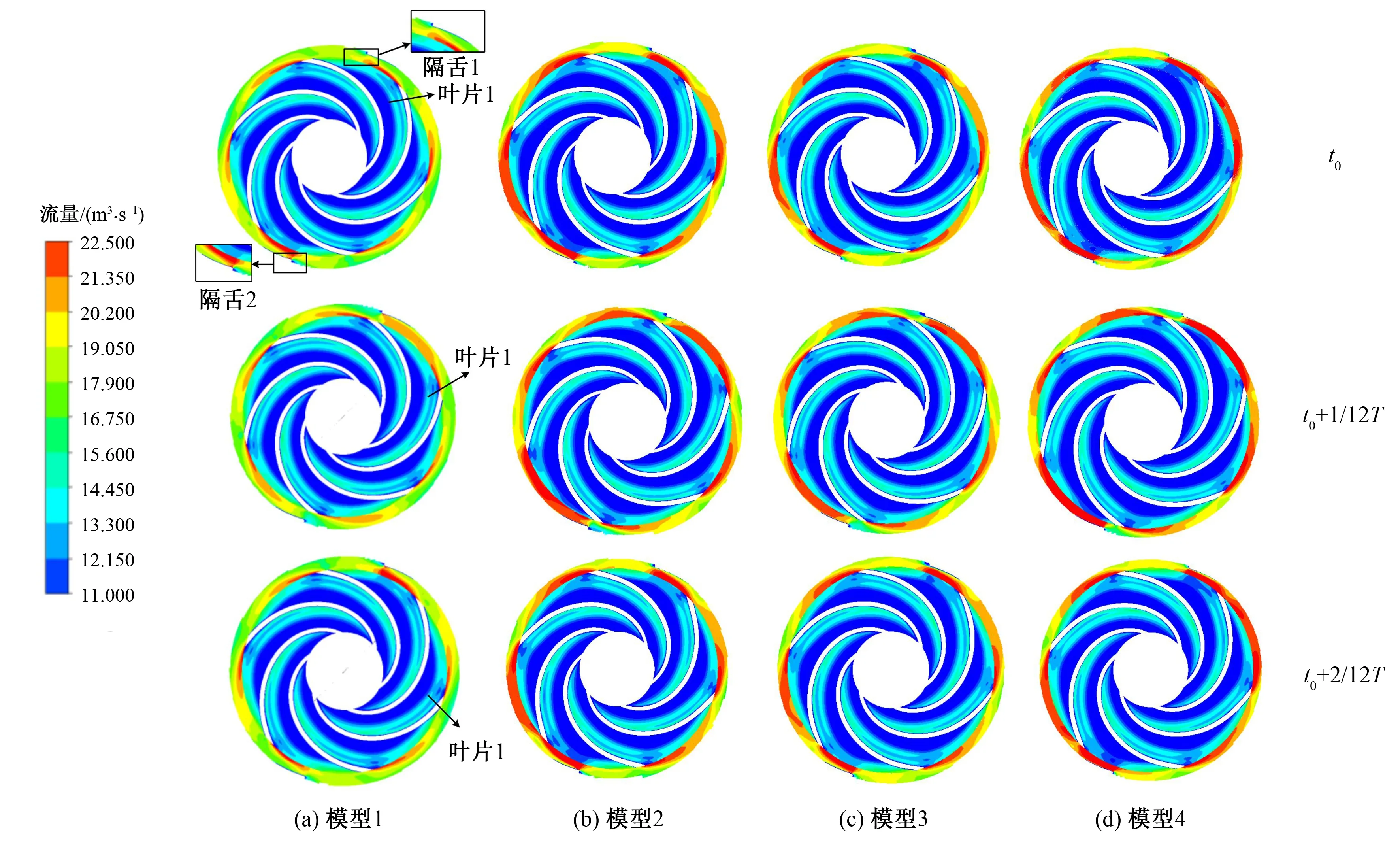
图6 额定工况下不同叶轮直径泵模型速度周期分布Fig.6 Velocity distribution of pump models with different impeller diametersunder rated conditions
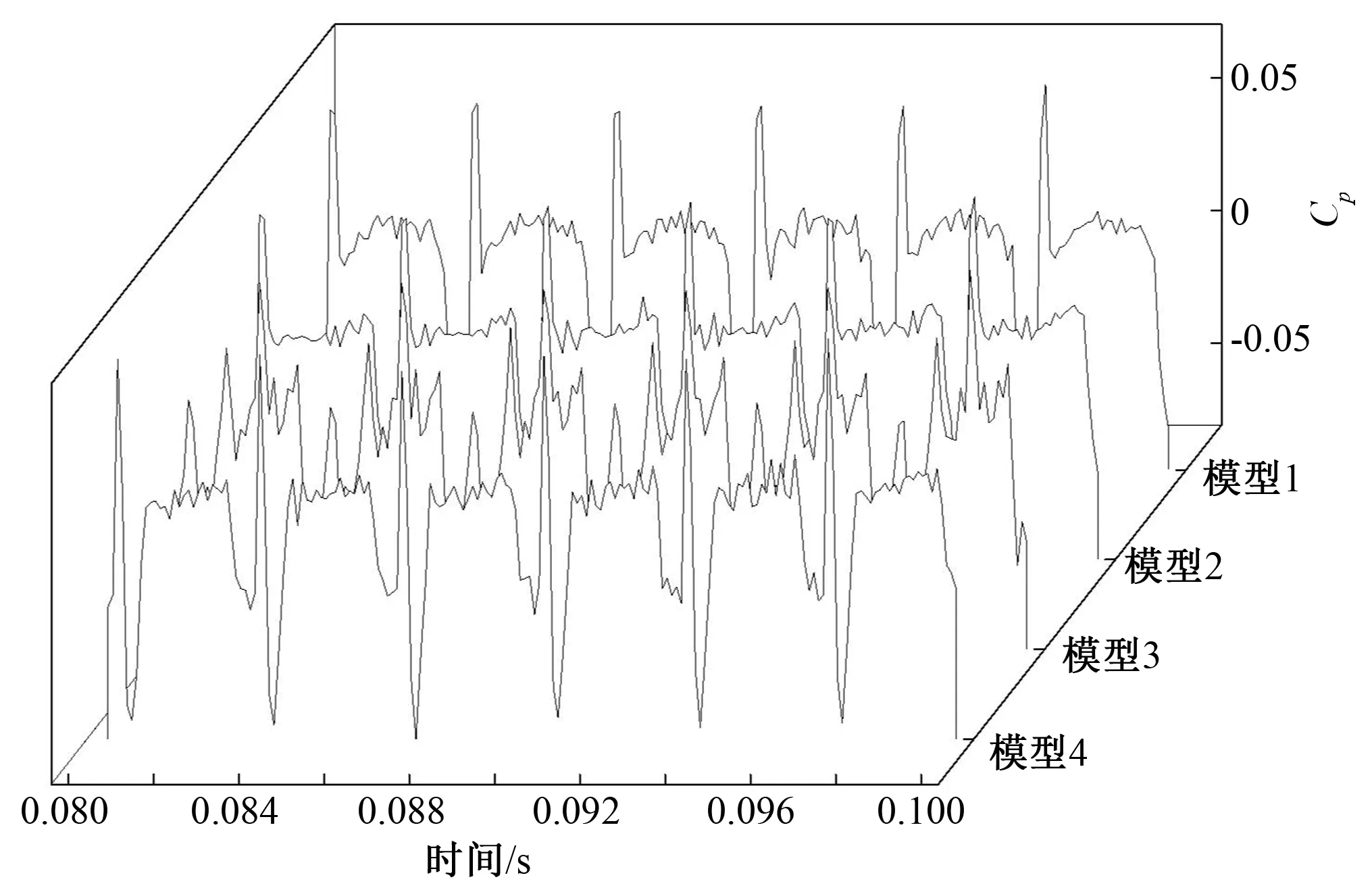
图7 模型泵压力系数时域图Fig.7 Model pump pressure coefficient time domain diagram
4 结 论
本文对不同叶轮直径下的双蜗壳离心泵进行压力脉动频谱分析。主要结论如下。
(1)受动静干涉作用的影响,不同叶轮直径的双蜗壳离心泵在叶片通过频率及其高次谐波处会出现脉动幅值的波动;
(2)小流量工况下脉动幅值高于其他流量工况,脉动强度会随流量增大逐渐减弱;在所选模型中,除隔舌区域监测点之外的其他监测点处压力脉动峰值处的脉动幅值随叶轮直径增大逐渐增大,且最大幅值波动达到23.8%。;模型3隔舌区域脉动幅值明显低于其他模型,且最大幅值波动为38.2%;
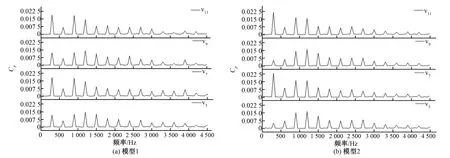

图8 不同叶轮直径下蜗壳周向测点频域分布图Fig.8 Frequency domain distribution of circumferential measuring points of volute under different impeller diameters
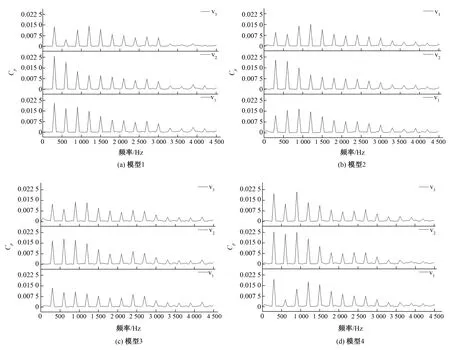
图9 额定工况下不同叶轮直径下隔舌测点压力脉动频谱Fig.9 Pressure pulsation spectrum of the tongue at different impeller diameters under rated conditions
(3)叶轮和蜗壳内流体流动过程中由动静干涉和射流-尾迹同时作用会使脉动产生叠加[nfBPF(n=1,3,4)],随着叶轮直径的改变,叶轮流道面积发生变化,使得射流-尾迹对流动混合作用更加明显,隔舌区域流动混合最为剧烈。
□
