改进的非参数时间序列模型在地下水位动态预报中的研究

杨淇翔，张琼楠

(1.河南省水利勘测设计研究有限公司，郑州 450016；2.水资源高效利用与保障工程河南省协同创新中心，郑州 450045)

0 引 言

地下水位是衡量生态环境优劣和地下水资源的一个重要指标，开展地下水位动态预报对于科学研判地下水位演变规律、保护地质生态环境和分析评估地下水超采区治理工程效益重要的理论意义和实践价值，尤其是最严格水资源管理制度下对开展水资源“双控”行动意义重大。目前地下水动态变化预测的方法较多，概括来讲主要分为以有限差分法、有限单元法等数值法为基础的分布式参数数学模型和以人工神经网络模型、门限自回归模型、混沌理论等非线性时间序列预测理论为基础的集总式参数数学模型。应当指出，分布式参数模型虽然一定程度上地解决了解析法中要求的含水层均质各向同性、结构规则、分布无限等限制，但模型的建立需要大量水文地质数据作为支撑，同时模型对初始条件、边界条件具有较强的敏感性，决定了模型的预测结果有很大的不确定性；而集总式参数模型中，无论时间序列模型中的随机项自回归系数[1]、小波神经网络基础上遗传算法[2]、支持向量机中先验知识和适宜核函数的选用[3]等也影响着模型的预报精度。

可以看出，传统的时间序列预测应用研究主要集中于与神经网络模型、自回归模型等其他非线性理论的耦合[4-6]，模型结构和计算过程相对较为复杂，尤其对于缺乏长期实测资料且影响因子关系复杂不明确的时间序列存在一定的局限性。鉴于此，本文借鉴相似预测理论，探讨以最大相似度准则改进的非参数时间序列模型，并首次应用于地下水水位动态预测的研究中，以期为地下水水位动态预报提供新的研究思路。

1 改进的非参数地下水位动态预报模型建模步骤

设有地下水位时间序列Y={x(t)}(t=1,2,…,n)，鉴于含水层系统地下水位动态演变的滞后响应效应，即第t年地下水位x(t)取决于前m个相邻样本值x(t-1)，x(t-2)，…，x(t-m+1)，x(t-m)，定义集合Ai=[x(t),x(t+1),…,x(t+m-1)](t=1,2,…,n-m)的预测值为Ai的后续值x(t+m)。可简单理解为：作为因变量的第(t+m)年地下水位预测值x(t+m)是集合At中m个自变量元素(影响因子)的函数：

x(t+m)=f[x(t),x(t+1),…,x(t+m),x(t+m-1)]

(1)

对于预测后续值第(n+1)年地下水位x(n+1)，可采用基于最大相似度的地下水位动态预报的集对分析模型，分析集合An+1=[x(n-m+1),x(n-m+2),…,x(n-1),x(n)]与At的同一度、差异度和对立度关系。具体建模步骤如下：

(1)构造集合A1，A2，An-m和An+1及其对应的后续值x(m+1)，x(m+2)，…，x(n)和x(n+1)，如表1所示。m取值不宜过小，否则不能客观反映地下水位动态变化的滞后延迟效应；m取值也不宜过大，否则地下水位时间序列非线性关系不能准确表达，同时造成序列中变量间较强的相依性。m取值建议在区间4～6较为合适。

表1 地下水位时间序列构成的集合表

(3)根据已建立的分类标准，符号量化第(n+1)年地下水预测水位x(n+1)所对应的集合An+1=[x(n-m+1),x(n-m+2),…,x(n-1),x(n)]，集合An+1分别与(n-m)个集合At分别构造集对H(An+1,At)t=(1,2,…,n-m)，将集合An+1～At对应元素逐一进行同异反比较分析。统计符号相同(同一性)的个数，记为S；统计符号相差一级(偏同差异)的个数，记为F1；统计符号相差二级(全差异)的个数，记为F2；统计符号相差三级(偏反差异)的个数，记为F3；统计符号相差四级(对立性)的个数，记为P。计算各集对H(An+1,At)的联系度μt(An+1,At)。

(2)

式中：ωk为K个相似集合相对于集合An+1的权重，在数值上等于集合An+1中元素平均值与集合Ai元素平均值的比值。

2 实例分析

2.1 研究区概况

根据中牟县水文地质条件和地下水观测井分布情况，由于18号观测井位于极富水区，地下水位埋藏较浅，地下水位动态主要受黄河侧渗影响，变化类型为径流-补给型，年际与年内水位变化相对较大，因此可选取18号观测井验证改进的非参数地下水位动态预报模型在地下水位预报中有效性的。根据水文地质部门提供的地下水动态资料，本文以1999-2016年逐月浅层地下水埋深构建时间序列，其中以1999-2014年时间序列数据构建模型，以2015-2016年时间序列数据作为改进模型的验证。

2.2 地下水埋深动态预报

2.2.1 地下水埋深年内动态预报

2015年逐月地下水埋深值以1999-2014年月时间序列构建模型，2016年逐月地下水埋深值以1999-2015年月时间序列构建模型，为最大程度利用实测数据，2015年逐月地下水埋深值采用实测值。限于篇幅，本文以2015年5月地下水埋深为例详细说明基于相似预测理论以最大相似度准则改进的非参数时间序列模型的预测过程。

(1) 将1999-2015年5月数据按照表1构建12个集合A1～A12和当前集合An+1(A13)，如集合A1=(5.24,5.19,5.15,4.90,4.88)分别对应于1999-2003年5月地下水埋深时间序列，其后续值x(6)=5.10对应于2004年5月地下水埋深值，依此类推。

表2 均值标准差法标定预测精度等级

表3 集合A13的相似集合及其联系度(数)

(5)根据式(1)容易计算求出改进的非参数地下水位动态预报模型下2015年5月地下水埋深 的预测值为6.03 m。同理可以计算出2015-2016年其他月地下水埋深的预测值，结果见表4。为直观起见，图2～图3给出了基于改进模型的2003-2004年逐月地下水埋深预测值和实测值的时间序列图。

表4 中牟县18号观测井2015-2016年逐月地下水埋深改进模型预测值与实测值对比

表4说明：在2015-2016年共24个月的地下水埋深预测值和实测值拟合序列中，相对误差|δ|全部在20%范围内，符合《水文情报预报规范》(SL 250-2000)要求[7]。其中，|δ|≤5%有19个，占到79.2%；5%<|δ|≤10%有4个，占到16.6%；10%<|δ|≤15%有1个，占到4.2%。

图1 中牟县18号观测井2015年逐月地下水埋深预测值与实测值对比

图2 中牟县18号观测井2016年逐月地下水埋深预测值与实测值对比

另外，从图1～图2中可以看出，中牟县18号观测井2015-2016年年内逐月地下水埋深动态模型预测值与实测值具有较好的拟合优度，两者呈现较强的趋势性，即同时在人工开采占主导因素的每年7月地下水埋深达到最大值，在地表水体补给浅层地下水占主导因素的每年5-9月地下水埋深达到最小值。埋深值平均绝对误差为0.30 m，其中最小绝对误差仅为0.03 m，最大绝对误差在2015年8月达到0.68 m，在2016年6月达到0.54 m，这是由于6～8月处于黄河调水调沙时段，地下水侧向补给及受人类活动影响相对复杂，往往对应着峰值转变产生的随机因素突变，模型由此产生了较大的系统误差。

2.2.2 模型验证

(1)有效性和可靠度检验。模型的有效性和可靠度可以通过分析所建立地下水位时间序列模型的实测值与预报值的绝对误差、相对误差及合格点数的百分率等指标予以验证。本文采用后验差检验法对模型的有效性和可靠度进行验证[8]。将2015-2016年中牟县18号观测井地下水逐月埋深实测数据和模型预测数据为例进行后验差检验，检验结果见表5所示。

表5 改进的非参数地下水位动态预报模型后验差检验结果

由表5分析可知，改进的非参数地下水位动态预报模型应用于中牟县18号观测井2015-2016年地下水逐月埋深预测中，C值均小于0.35，小误差概率P均大于0.9，该模型泛化能力较好，预测精度较高。

(2)不同时间序列预测方法结果比较。为进一步说明本文提出的基于最大相似度准则的地下水动态预报模型的可靠性，考虑神经网络模型在时间序列预测中，过程较为烦琐且预测结果受网络节点、最小训练速率、动态参数、迭代次数、允许误差等影响较大，拟选取与本文提出的模型预测思路、理论和方法相对一致的门限自回归模型作对比分析。

以1999-2015年月时间序列构建门限自回归模型，预测2016年中牟县18号观测井地下水逐月埋深为例，门限变量延迟取2，模型延迟阶数取6，经数据标准化处理，门限值为5.156 9，相关系数为0.915 8，2016年18号观测井地下水逐月埋深预测值见表6。

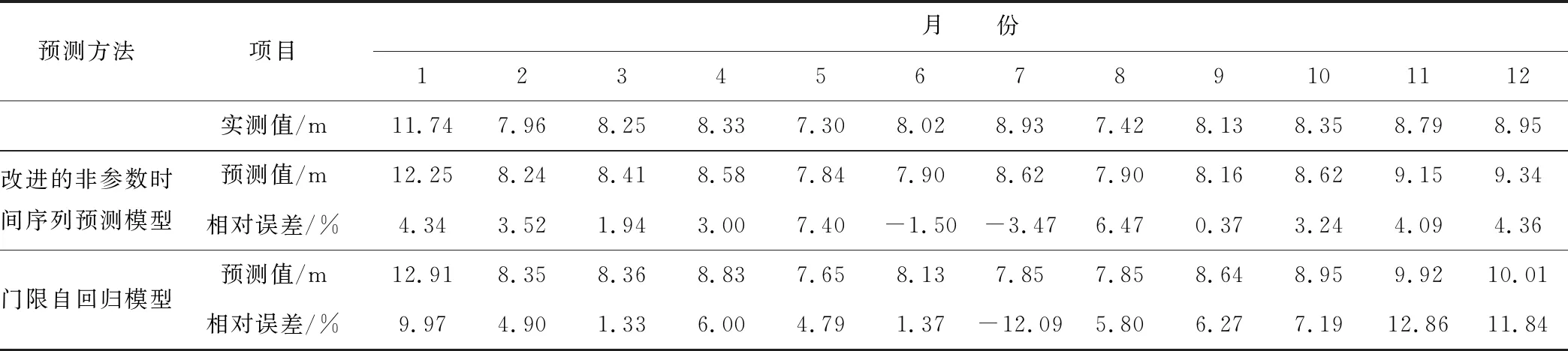
表6 本文模型与门限自回归模型预测结果比较

根据《水文情报预报规范》(SL 250-2000)，在2016年共12个月的地下水埋深预测值和实测值拟合序列中，本文提出的基于最大相似度准则的地下水动态预报模型和门限自回归模型相对误差均全部在20%范围内。但门限自回归模型相对误差|δ|≥10%有3个，占比25%；5%<|δ|≤10%有5个，占比42%；|δ|≤5%仅有4个，占比33%，相对本文提出的模型预报精度较低。门限自回归模型预报误差较大的月份出现在7月、11月和12月，主要原因是受黄河河道水位变化较大，侧向补给条件复杂等因素影响，延迟阶数范围内的最优回归模型拟合度较差，地下水位预报精度降低，而本文提出的改进的非参数时间序列预测模型可以最大程度利用多个最相似的历史样本的地下水位，减小系统随机误差，提高预报精度。

2.3 结果分析

(1)本文提出的五元联系度模型刻画了地下水时间序列中集对H(An+1,At)的同一度、差异度以及对立度的复杂非线性关系结构，不确定性关系能够定量予以表示。例如，表4中在预测中牟县18号观测井2015年8月地下水埋深中，集合An+1(A13)与集合A6的同异反联系度向量(0,0.4,0.4,0.2,0)表示对应元素均值标准差标定的等级下，集对(A13,A6)中对应元素等级相同的同一度为0，相差1级的偏同差异度为0.4，相差2级的全差异度为0.4，相差3的偏反差异度为0.2，相差4的对立度为0。

(2)改进的非参数地下水位动态预报模型从同异反联系度的角度来测度地下水位时间序列历史样本之间的相似性，以最相似历史样本的地下水位作为设定月(年)地下水位的预测值，为地下水位动态预报提供了新颖的研究思路。此外，本文提出的地下水埋深模型改进了传统统计预报理论的模式，即预报函数形式是随着历史数据资料变化而变化的。因此，基于样本之间最大相似度的预报模式符合地下水文系统的实际演变情况。表4从绝对误差-相对误差的角度，说明改进的非参数地下水位动态预报模型应用于地下水埋深预报中具有较高精度，达到了相关规范要求；图2～图3直观表明预测值与实测值具有较高的拟合度，年最大埋深月份和最小埋深月份等趋势性基本保持一致，符合观测井区域补径排特征和动态变化特性。总体来讲，改进的非参数地下水位动态预报模型依据科学合理，计算过程简单有效，在时间序列分析预测中具有较好的推广应用前景。

3 结 语

本文提出的改进的非参数时间序列预报模型在地下水位动态预报中的应用以定量的形式描述了的样本间的相似度，如何更准确、客观地量化联系度是提高地下水位动态预报精度的关键问题，而差异度不确定性系数I的取值是值得深入探讨的。本文的重点在于阐述集对分析在地下水位动态预报中的应用研究，而差异度不确定性系数I1、I2和I3的取值为方便起见采用特殊值法分别赋值为-0.5、0、0.5，但特殊值法有可能成为地下水位动态预报中相对误差偏大、预报精度偏低的原因之一。以2015年8月的埋深值预测为例，预测绝对误差为0.68 m，相对误差达到10.78%，而此时历史样本之间的最大相似度(联系数)为0.4，也就是说以联系数0.4作为最大相似度是值得商榷的。

因此，三角模糊数法[9]、梯形模糊数法[10]以及文献[4]提出的马尔科夫理论优化差异度不确定性系数等方法为深入研究I的合理取值提供了理论指导。同时，本文基于均值标准差法对集合At中各个元素进行了等级分类和符号化处理，在此基础上界定了集对H(An+1,At)的同一度、差异 度和对立度，但尚缺乏坚实的科学基础，也需要对集对分析原理进行深度探索。以文献[9]提出的以三角模糊数确定联系数为例，针对差异度系数I在区间[-1,1]连续变化特征，可引入α截集和置信区间概念，确定不同α取值条件下置信区间长度的变化规律，以置信区间形式而不是一个固定值预定地下水位埋深是值得深入研究的。

此外，地下水系统是一个受水文地质条件控制,并受降雨、气候和人类工程活动等多种因素影响而发展演化的非线性耗散动力结构, 内部各因素之间以及内部因素与外部因素之间存在着复杂的交互作用和因果关系，并且具有明显的混沌特征。对于联系数的确定，还需进一步探讨研究如何在集对分析框架下与随机性、灰色性、模糊性、未确知性、分形和混沌等其他理论耦合以定量深入表征不确定性关系。混沌理论中的相空间重构技术从实际单因变量时间序列拓扑为动力学系统吸引子结构未改变的高维空间，包含了系统所有变量长期的演化信息。因此，从相空间重构的角度出发寻求时间序列的混沌特征、时间延迟τ和嵌入维数m的确定方法，构建混沌-集对分析耦合模式进行降水-径流、地下水动态预报等水文预测将成为时间序列新的研究方向和热点，同时对于优化联系数取值、提升集对分析应用研究也具有重要的意义。

□