渐进演化类拓扑优化算法的优化准则对比研究

2020-06-15张鹄志张棒谢献忠马哲霖

土木与环境工程学报 2020年3期

张鹄志，张棒，谢献忠，马哲霖

(湖南科技大学 a.土木工程学院；b.结构抗风与振动控制湖南省重点实验室，湖南湘潭 411201)

近20年来，结构拓扑优化成了实现结构轻量化的重要手段之一，这是一种根据设计区域、优化目标、设计载荷等约束条件来寻找结构最优材料分布的优化方法。优化结果被广泛应用于建筑、机械、航天、海洋工程等领域。随着相关研究的深入，渐进类拓扑优化演化算法得到了不断的改进和优化，取得了不少研究成果。

渐进结构优化(简称ESO)算法[1-3]最早由Xie等提出，并证实其具有高效性和稳定性的特点。荣见华等[4-5]利用ESO算法对车辆结构进行优化设计，验证了ESO算法在机械工程领域中的应用价值，王磊佳等[6]对ESO的删除准则进行改进，提出了加窗渐进结构优化算法。Querin等[7]提出了与ESO优化进程相对的算法，即在高应力区域逐渐添加材料，以获取拓扑解的递增演化结构优化(简称AESO)算法。之后，Xie等[8]、Rozvany等[9]、Yang等[10]又在此基础上提出结合AESO与ESO的双向演化结构优化 (简称BESO)算法，母德强等[11]使用BESO算法实现了对大型龙门工程机械横梁的拓扑优化。江旭东等[12]利用BESO算法实现了结构多目标动态优化设计。而随着王小平等[13]对遗传算法的推广，易伟健等[14]将ESO算法和遗传算法结合，提出遗传演化结构优化 (简称GESO) 算法，提高了这类算法全局寻优的能力，张玉顺[15]利用GESO算法完成了钢筋混凝土三维构件拓扑优化方法，张望喜等[16]在GESO基础上提出了遗传递增演化结构优化算法(简称GAESO)。

当前，ESO、BESO和GESO等3种算法均可以稳定地获得拓扑解，但由于其优化准则的差异，使得3种算法对同一构件完成优化时结果不尽相同。由此，以简支深梁为算例，针对渐进演化类拓扑优化算法的优化准则进行对比研究，一方面讨论确定性优化准则和概率性优化准则的差异，另一方面探索单向优化准则和双向优化准则的差别，讨论不同的优化准则造成优化过程和优化结果上的异同，并分析造成这种现象的原因，以探讨不同优化准则的优劣和适用范围。

1 渐进演化类拓扑优化算法对比

1.1 算法基本思想

渐进演化类算法的基本思想是先利用有限元软件，对结构进行力学分析，借助分析结果获取每一个单元的灵敏度并对之进行排序，以此判断单元对于结构性能指标的贡献度，再基于算法使用的优化准则，逐步删除对整体结构性能指标贡献较低的单元或者增加对结构性能指标贡献较大的材料，促进结构向最优化解演化，最终使得结构能够在满足特定性能指标的前提下尽可能地降低材料的消耗，从而降低建造成本。

1.2 确定性和概率性的优化准则

优化准则是获取最优拓扑的关键一环，有多种分类方法，第一种是按选择优化单元的方式分为确定性优化准则和概率性优化准则。确定性优化准则是指在优化过程中选择删除的无效材料或增加的有效材料完全根据应力计算结果，优胜劣汰，如ESO算法即采用这种优化准则；概率性优化准则有所不同，如GESO算法即加入遗传算法的遗传和突变特性，以改变每代删除或添加的单元位置和数量，实际选择优化单元的方式具有一定的随机特性，所以，重复一次完整的优化过程可能会得出有所区别的解，但大多数解应该大同小异。

1.3 不同优化方向的优化准则

优化准则的另一种分类方式是按优化方向进行划分，当前包括正向优化、反向优化以及结合两者而形成的双向优化方法。正向优化即初始域是满设计域，优化过程单向删除低效和无效材料，演化出最优拓扑解；反向优化则刚好相反，初始域仅存在必要单元，优化过程单向补充高效材料，演化出最优拓扑解；双向优化则取两者所长，既可能从正向优化开始，也可能从反向优化开始，但伴随优化的进行，迭代过程维持着一边删除低效和无效材料，一边补充高效材料的双向演化状态，最终演化出拓扑解。

2 优化准则的确定性与概率性

从材料力学来看，深梁不满足平截面假定，属于典型的复杂受力构件，与适用于传统抗弯和抗剪理论的浅梁受力有明显区别。以深梁为例，探讨采用确定性优化准则的ESO算法和采用概率性优化准则的GESO算法的差异。算例均以ANSYS有限元软件为平台，假定结构材质均匀，各向同性，且所有结构处于平面应力状态，因此，选用PLANE82单元将钢筋和混凝土视为复合材料，对其线弹性行为进行模拟，建模时输入的材料弹性模量为E=3.0×104N/mm2，泊松比为v=0.2，网格划分时单元尺寸设定为20 mm×20 mm，对结构进行线弹性分析，即仅考虑结构弹性阶段的变形，忽略裂缝的开展和塑性阶段的变形，在此参数设置下建立的有限元模型可以模拟钢筋混凝土共同工作下梁弹性阶段的受力变形情况。ESO算法每代淘汰单元个数为20，GESO算法中杂交率为0.2，变异率为0.2，最优个体选择率为0.3。ESO算法和GESO算法的具体操作流程和淘汰率选取分别依据文献[1]和文献[14]的建议。

2.1 简支开洞深梁数值算例

由于结构功能的需要，荷荷载有时作用于深梁下部，形成所谓的吊挂荷载，如料仓、水箱的侧壁以及高层建筑的墙梁等都属于下部受荷深梁。对三点承载的简支开洞墙梁[17]进行优化，算例的结构尺寸为2 000 mm×1 000 mm，有两个对称洞口，洞口尺寸均为500 mm×500 mm，洞口位置及其他具体的几何尺寸如图1所示，梁底四分点处分别施加大小为P=40 kN的3个集中荷载，ESO算法的优化过程如图2所示，GESO算法的优化过程如图3所示。

从图2(b)和图3(b)可以看出，对于多点加载的简支开洞深梁，两种算法初期即在跨中的受压区表现出显著的差别，且造成该区域接下来优化过程中腹杆角度及腹部间拉杆位置的明显差异(如图2(c)和图3(c)所示)，该区域的最优拓扑也有着较大的区别，ESO的两根斜压杆在底部交于一点，而GESO的两根斜压杆向下分别转成竖直压杆，形成了两条完全不相交的压力路径(如图3(d)和图4(d)所示)。

经统计，ESO算法比GESO算法节省时间50%～60%。这是由于GESO算法需要进行遗传的仿生过程，每一次迭代都需要进行选择、杂交和变异，造成优化效率下降。由此可见，ESO尽管优化能力略弱于GESO，但却有着更高的优化效率。

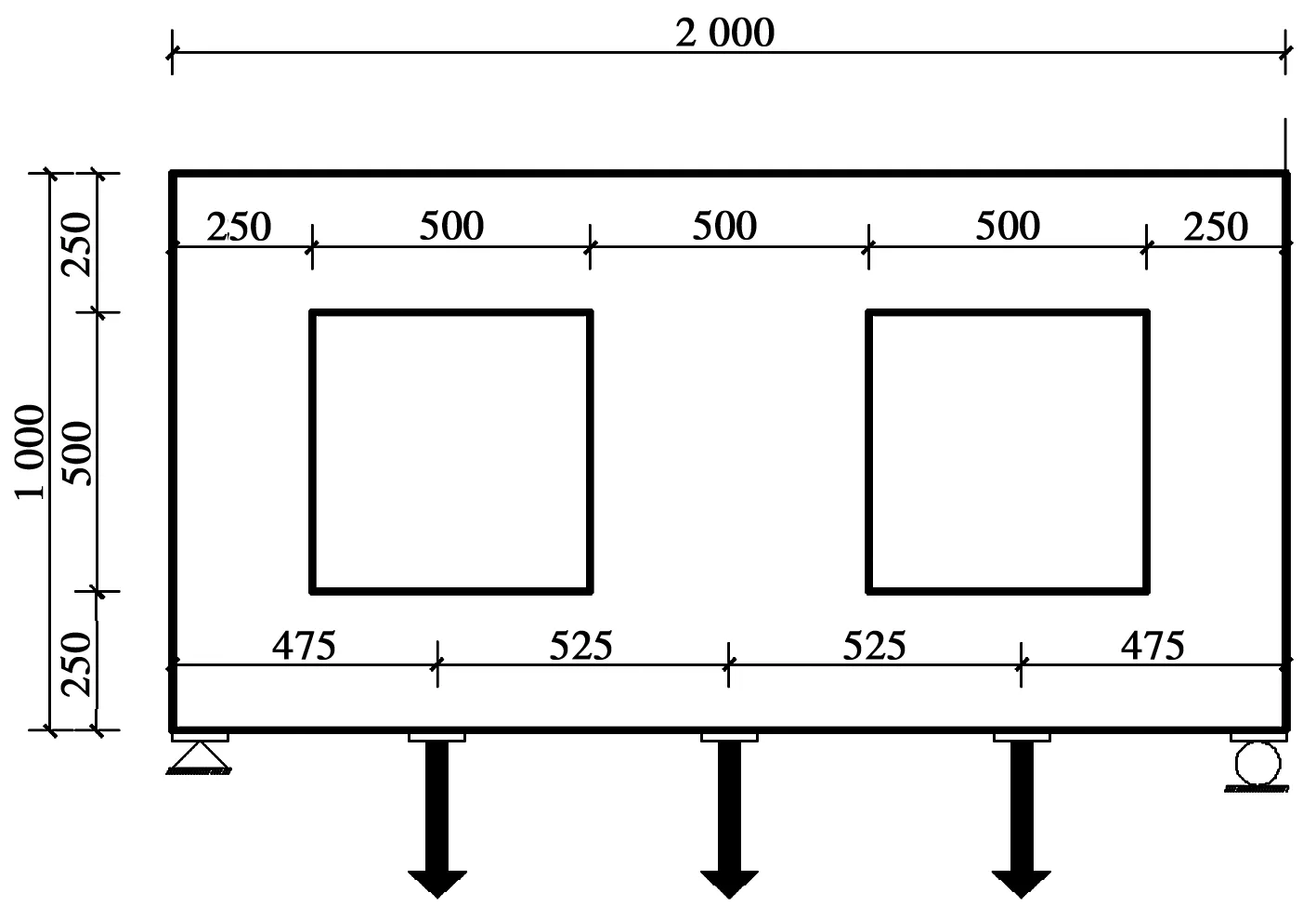
图1 简支开洞深梁几何尺寸Fig.1 Dimension of simply supported deepbeam with openings

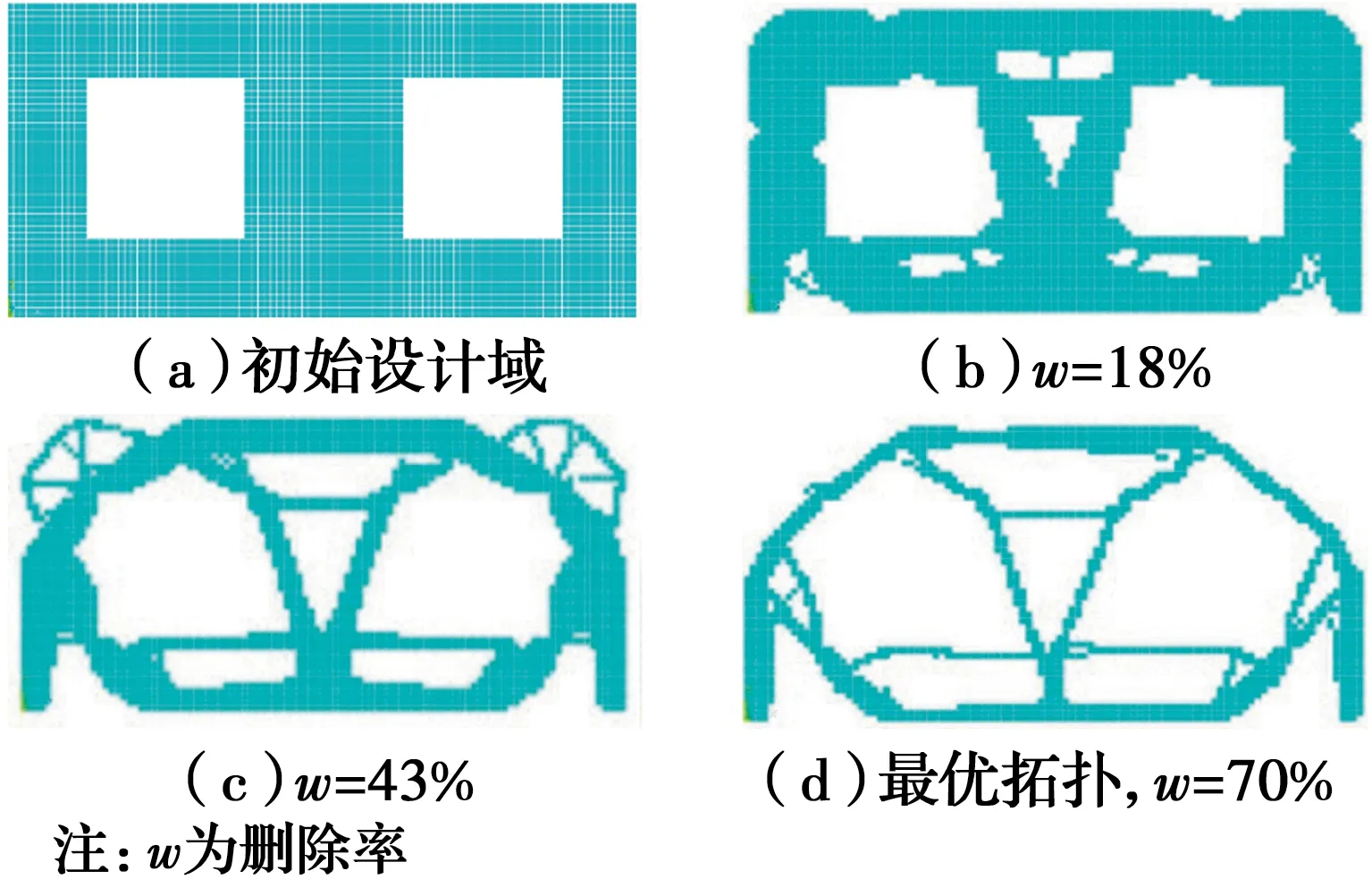
图2 简支开洞深梁ESOFig.2 ESO of simply supported deep beam with openings

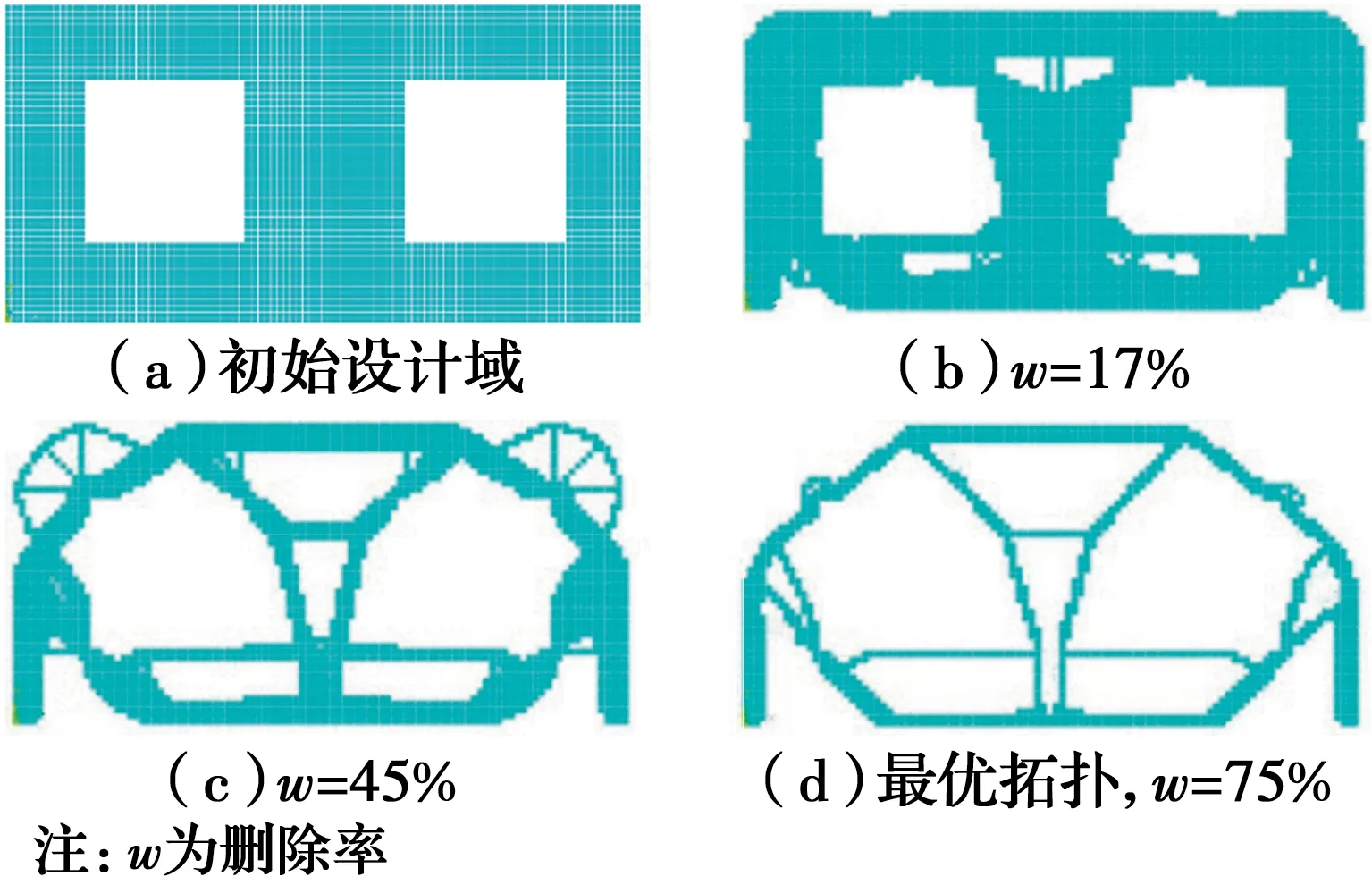
图3 简支开洞深梁GESOFig.3 GESO of simply supported deep beam with openings

2.2 算例结果分析

两种算法的优化过程表现出较大差异，这是因为：

1)ESO采用每代固定删除单元数量或者删除率，当部分区域内单元的灵敏度值十分接近时，也可能因删除数量和浮点精度的影响而产生不对称的单元删除，并在随后的优化过程中因应力重分布和应力集中加剧这种畸变现象。而GESO则会在计算完灵敏度后对单元进行变异和杂交等遗传过程，再计算单元的适应度和每个单元被删除的概率，正是因为这种全设计域内概率性选择删除方式，GESO一方面很大程度上降低了浮点计算精度产生畸变的可能，另一方面，即使早期少量畸变的发生，之后的概率性选择删除也能在一定程度上消除这种畸变。

2)根据文献[18]推导的此类结构的Michell桁架解(符合满应力的解析解)，压杆之间的夹角整体上是均匀分布的，对称轴附近适当减小。对比两种算法下的拓扑解，GESO结果中一直保持着Michell桁架解的压杆分布特性(如图3(c)和图3(d)所示)，其结果中上部斜拉杆的夹角要明显小于ESO优化结果中的上部斜向拉杆(如图2(c)和图2(d)所示)，GESO的优化结果稳定性要明显强于ESO优化结果。由此可知，GESO对于复杂应力构件的优化又优于ESO算法。

对于荷载条件、边界条件或传力路径较模糊的构件，确定性优化准则误删单元的可能性更大(根据实例研究所知，对于受力简单传力路径明显的结构，ESO算法和GESO算法优化结果十分相似，误差易收敛)。从图2(d)和图3(d)还能看出，ESO算法的优化程度只达到了70%，较GESO算法低5%，当对处于吊挂荷载下的开洞深梁这类传力路径复杂的构件进行优化时，ESO得到的最优拓扑的棋盘格现象和优化畸变均要大于GESO得到的最优拓扑，如各杆相交的节点处，不论对称性还是演化出杆件的清晰度，GESO都略胜一筹。

3 优化准则中的优化方向

以深梁为例，探讨优化准则中优化方向对优化过程及结果的影响。有限元分析参数及优化参数的选取基本与2.1节算例相同，BESO设定每代淘汰单元数为20，复活单元数为5，具体操作流程和优化参数选取参考文献[2]。

3.1 固支开洞深梁数值算法

考虑到边界条件越复杂，结构受力就越复杂，早期误删单元的可能性也越大，在寻求这种情形下的全局最优解时，加入复活机制形成双向优化准则，优势也更明显，故选用与2.1节相同的构件尺寸和荷载条件，但将原有的两端简支换成了两端固定支座，如图4所示，ESO算法的优化过程如图5所示，BESO算法的优化过程如图6所示。

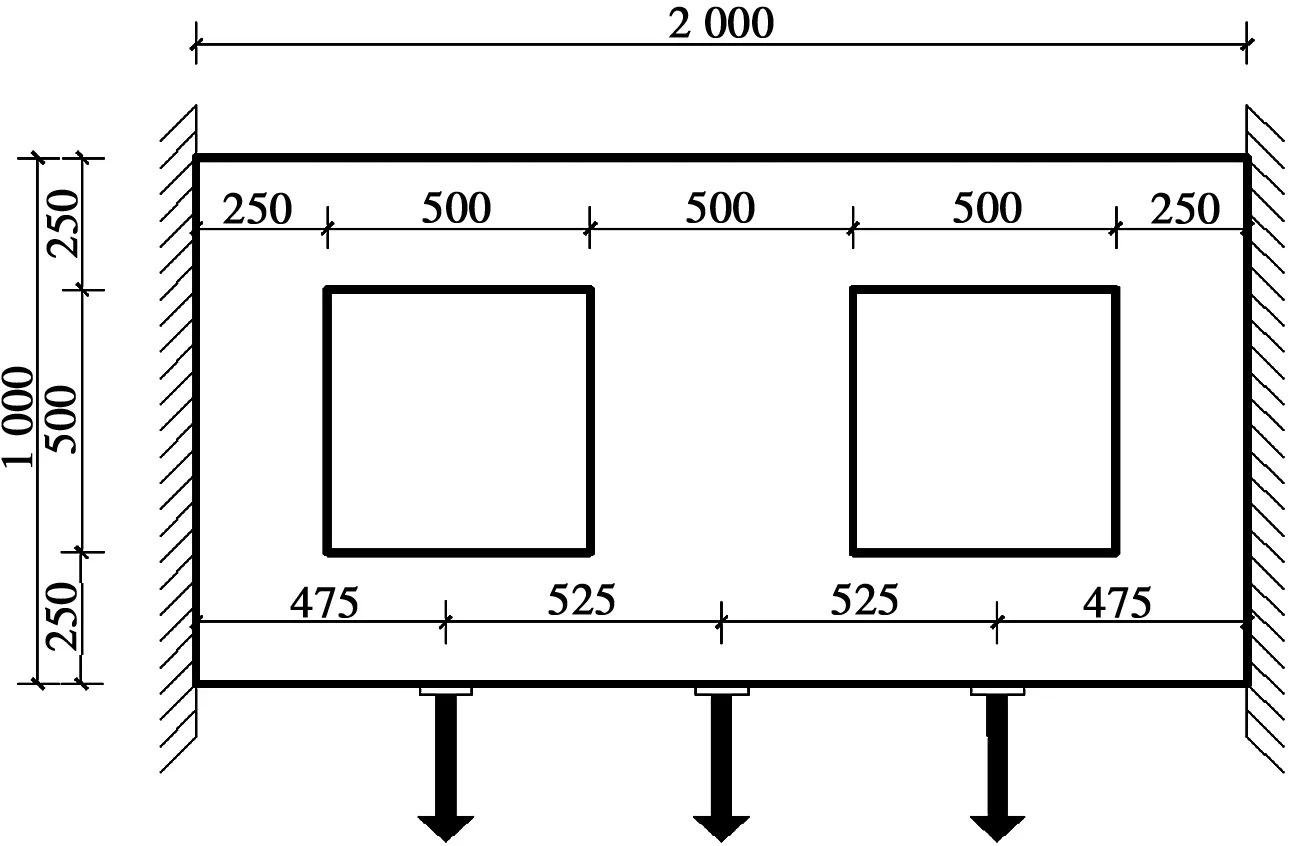
图4 固支开洞深梁几何尺寸Fig.4 Dimension of fixed-fixed deep beam with openings

图5 固支开洞深梁ESOFig.5 ESO of fixed-fixed deep beams with openings

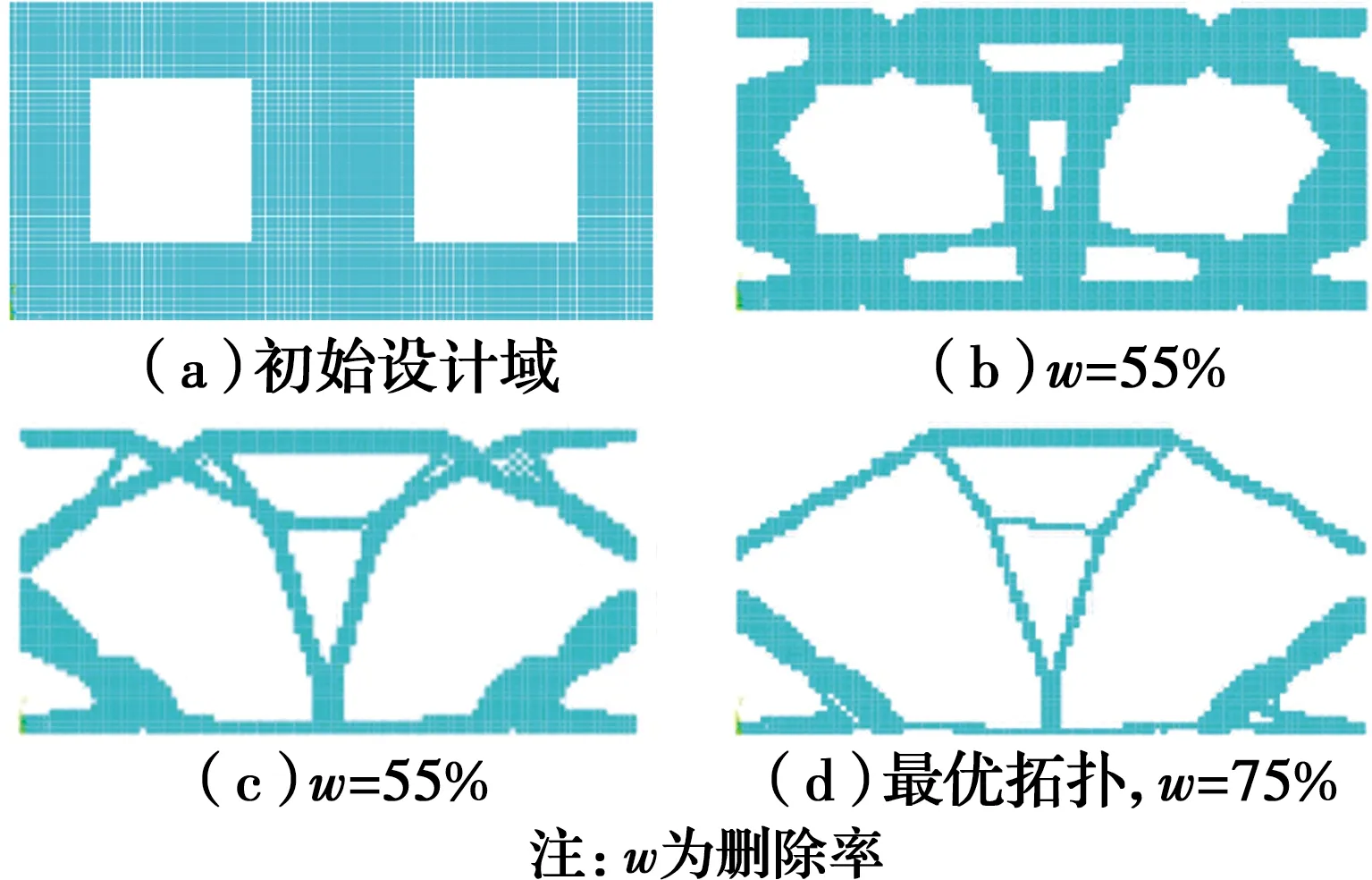
图6 固支开洞深梁BESOFig.6 BESO of fixed-fixed deep beams with openings

从图5(b)和图6(b)可以看出，两种算法初期差别不太大，仅ESO在跨中局部出现不对称拓扑的小幅畸变，整体上结构左侧单元数量略多于右侧单元，在后续优化过程中，这一畸变效应产生的不对称拓扑继续发展，在整个结构顶部尤为明显(如图5(c)和图6(c)所示)，最终得到的最优拓扑，ESO算法较BESO算法多删除3%的单元量，ESO算法的结果依然在顶部呈现明显的不对称(如图5(d)和图6(d)所示)；而BESO在整个过程中对称性保持良好，仅在最后阶段两侧底部出现轻微不对称畸变，且该畸变对最优拓扑影响不大。此外，与ESO略有不同的是，BESO的最优拓扑在跨中腹部保留有一根水平系杆。

经统计，ESO算法比BESO算法节省时间一半以上。这主要是因为BESO算法在完成类似ESO算法的灵敏度计算以删除部分单元后，还需要对当前被删除的所有单元进行二次灵敏度的计算以复活部分单元，所以优化耗时更长。

3.2 算例结果分析

两种算法的优化过程和拓扑解表现出一定异同，这是因为：

1)首先，根据文献[18]推导的此类结构的Michell桁架解(符合满应力的解析解)展开分析可知，由于洞口位置对上部压杆分布的影响，该结构的跨中腹杆不可能为一根竖直拉杆，图5和图6中的斜腹杆分布很大程度上符合Michell桁架解的杆件分布特性。

2)仔细对比可以发现，图6(d)所示的BESO拓扑解中，跨中腹部水平系杆的两端结点处，上下的斜腹杆间存在小角度的夹角，而图5(d)所示的ESO拓扑解中，该位置没有折角，对这两个拓扑解建立桁架模型完成结构力学计算可知，一方面，图6(d)中这根水平系杆对于保证其两侧的压杆稳定有着重要的意义，另一方面，图6(d)中斜腹杆的轴力小于图5(d)中的斜腹杆。由此可见，BESO寻得的拓扑解优于ESO。

3)BESO比ESO寻优能力更强的原因在于其优化准则中存在的复活机制，当发生类似ESO过程中删除单元引起拓扑优化进程向局优解或畸变发展时，能够通过对被删除单元进行灵敏度二次计算，复活一定比例的单元，三点加载的两端固支开洞深梁相较于2.1节中的简支开洞深梁具有更为复杂的边界条件和传力路径，BESO的双向优化准则一方面能在较大程度上消除畸变，另一方面可以对陷入局优的拓扑解逐渐修正，所以，BESO较之ESO拥有更强的全局寻优能力。

4 遗传双向渐进演化结构优化算法

单向和确定性优化准则的ESO算法，在面对较复杂的工程对象时，易于优化早期误删单元，导致优化过程出现畸变或陷入局部最优。GESO算法引入遗传算法的概率思想，可以在一定程度上避免因确定性优化准则造成的误删；而BESO算法则通过改进出双向优化准则，前期的误删单元有了被复活的可能，同样能避免过早删除最优解单元的问题。GESO算法的概率性优化准则和BESO算法的双向优化准则均能在很大程度上减少优化过程中误删单元的问题，避免优化结果陷入局部最优解。

然而，GESO终因不可复活误删单元而存在局限性，BESO也终因确定性的优化准则而存在一定的弊端，所以它们的全局寻优能力依然还需进一步加强。将概率性优化准则和双向优化准则结合，发展出遗传双向渐进演化结构优化 (简称GBESO) 算法是一条显而易见的思路，其操作流程如图7所示。在利用GBESO进行第2节和第3节的开洞深梁拓扑构造时，拓扑解呈现出一定的畸变，这可能是由于开洞后直接的传力路径受到阻碍，引起拓扑解复杂化，而当前对GBESO的开发还处于起步阶段，对淘汰机制和复活机制间的权重关系研究还不充分，故仅以未开洞的简支深梁作为算例，简要展示GBESO过程，构件尺寸及拓扑优化分别如图8和图9所示。

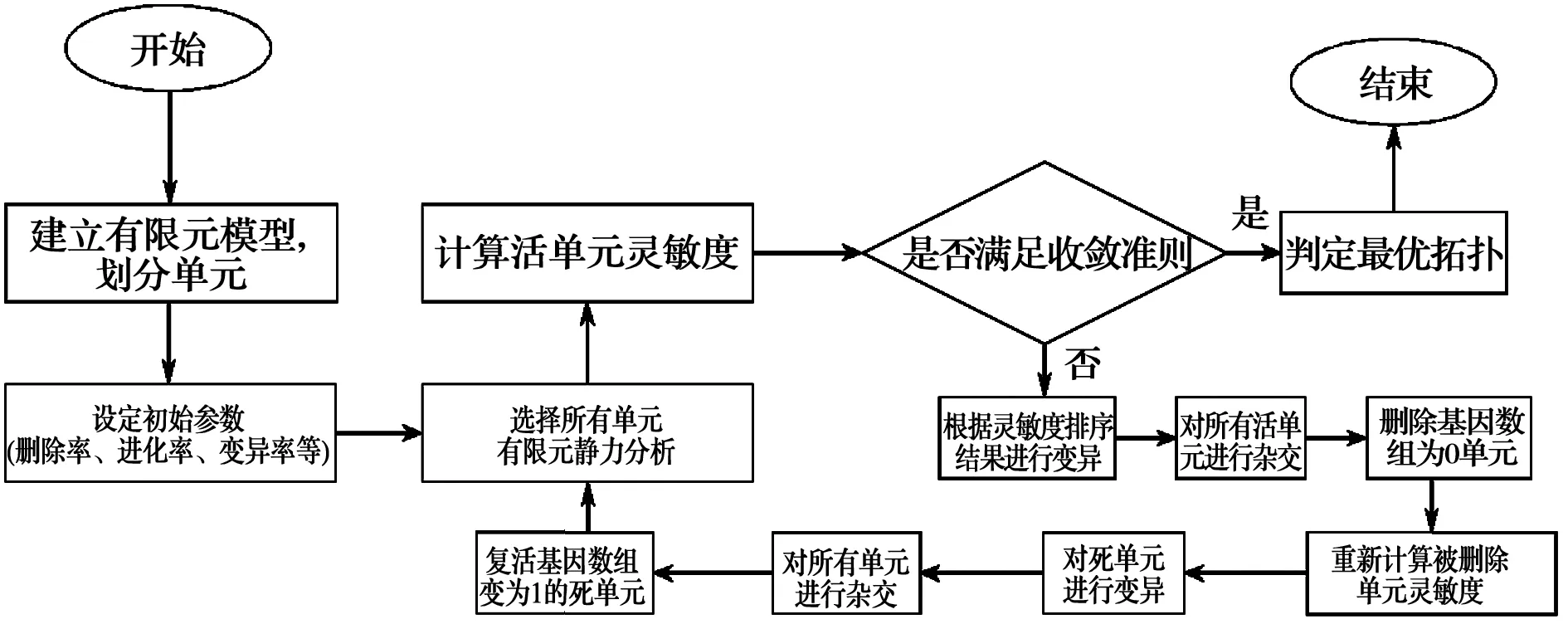
图7 GBESO算法流程图Fig.7 Flow chart of GBESO algorithm

图8 简支深梁几何尺寸Fig.8 Dimension of simply supported deep beam

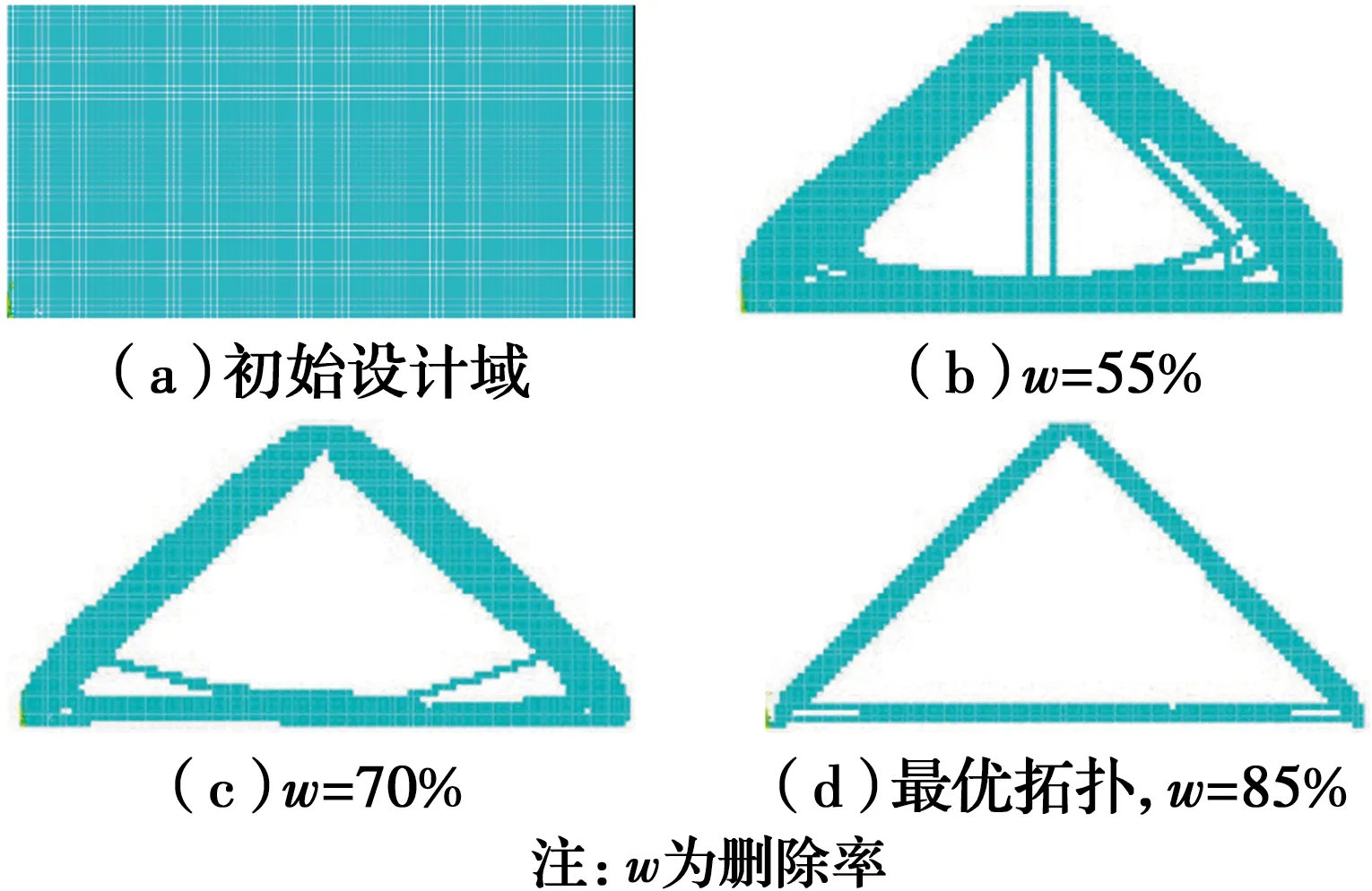
图9 简支深梁GBESOFig.9 GBESO of simply supported deep beam

GBESO算法先使用遗传算法对单元进行变异和杂交，初次删除的单元中仅包含少数高应力单元，随后使用双向优化准则，对被删除单元进行第二次灵敏度计算，复活其中被删除的单高应力元，进一步减轻误删单元造成的结构畸变现象以获取全局最优解。当然，一方面，算法的实现有待落实，算法的稳定性、普适性等多方位的性能也有待进一步验证；另一方面，随着概率性复活单元操作的加入，GBESO算法的优化效率可能会较GESO和BESO算法进一步降低，这也有可能成为限制其工程应用的一大障碍。