磁流变阻尼器拟静力力学特性及力学模型

2020-06-15张香成毋贵斌赵军

土木与环境工程学报 2020年3期

张香成，毋贵斌，赵军

(郑州大学力学与安全工程学院，郑州450001)

磁流变阻尼器(Magnetorheological damper, MRD)是一种可调节阻尼的减振控制装置，具有结构简单、出力大、阻尼力连续可调且控制效果好的优点，在土木工程减振防灾方面展现出了良好的应用前景，已成为目前结构振动控制的重要装置[1-7]。近年来，学者们对MRD做了大量研究，梅真等[8]对MRD进行了动力学试验，建立了双曲正切滞回模型和BP神经网络正向、逆向力学模型，并对这两种模型进行验证；杜成斌等[9]对MRD在低频下力学性能进行研究，并对非线性滞回双粘性模型进行了修正；张香成等[10]基于米氏方程提出了米氏模型，并通过试验加以验证。

对设置MRD的结构(或结构构件)进行拟静力试验是研究其力学性能、耗能性能和二者相互作用机理的经济、可靠手段，然而，关于MRD拟静力性能的研究较少，因此，在研究设置MRD结构(或结构构件)的力学性能之前，应当先对MRD的拟静力性能进行研究。Zekeriya等[11]采用准静态分析的方法研究了MRD中的非牛顿流动，并对MRD进行了计算流体动力学分析；Mohammad等[12]对MRD中的磁流变流体流动进行了准静态分析，说明了磁流变流体惯性产生的影响，但这些研究并未描述MRD的拟静力力学性能。

笔者采用位移加载方式，利用三角波加载函数在低速下对自制的MRD进行拟静态加载，得到不同工况下MRD的阻尼力-位移曲线。通过对结果进行对比分析，研究MRD在不同位移幅值、不同电流下的力学性能，分析试验中MRD阻尼力波动等现象出现的理论原因。基于试验结果提出一种拟静力作用下修正的MRD阻尼力计算模型，并对力学模型中的参数进行了识别。

1 阻尼器拟静态试验

1.1 阻尼器结构

采用四线圈剪切阀式阻尼器，阻尼器多级活塞材料为电工纯铁，其余部分为45号钢，其结构如图1所示。基座连接板利用螺栓将阻尼器与下方基座连接，线圈导线从MRD多级活塞和活塞杆中心的圆柱形孔道引出。阻尼器各部分参数见表1。

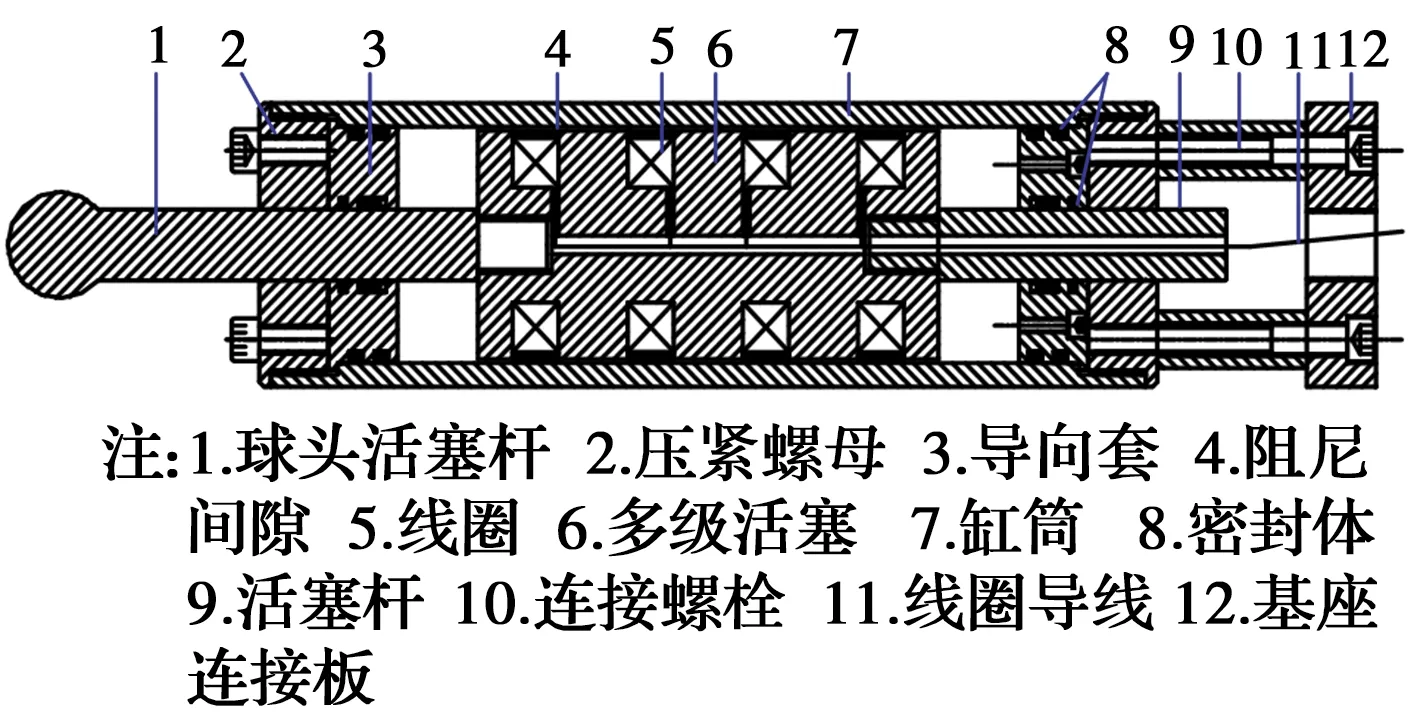
图1 多线圈剪切式MRD结构构造图Fig.1 Structuralchart of multi coil MRD

行程/mm线圈电阻/Ω线圈槽深/mm活塞杆直径/mm±354×8.52496.8阻尼间隙/mm缸筒内径/mm缸筒外径/mm线圈匝数(n×turns)1.61001204×840

阻尼器内部填充的磁流变液采用自制方法获得，其组分为羰基铁粉、硫酸钠、液体石蜡、皂土、石墨以及甲基硅油等，其中，羰基铁粉占60%、甲基硅油占28%(质量分数)。磁流变液的相关性能在中国科学技术大学智能材料与振动控制实验室测定，在磁场强度为0.44 T时，当剪切速率分别为0.01、0.34/s-1时，磁流变液的剪切应力分别为9 456.2、9 492.2 Pa，二者相差0.38%；当剪切速率为100/s-1时，磁流变液在不同磁场下的剪切应力见表2。

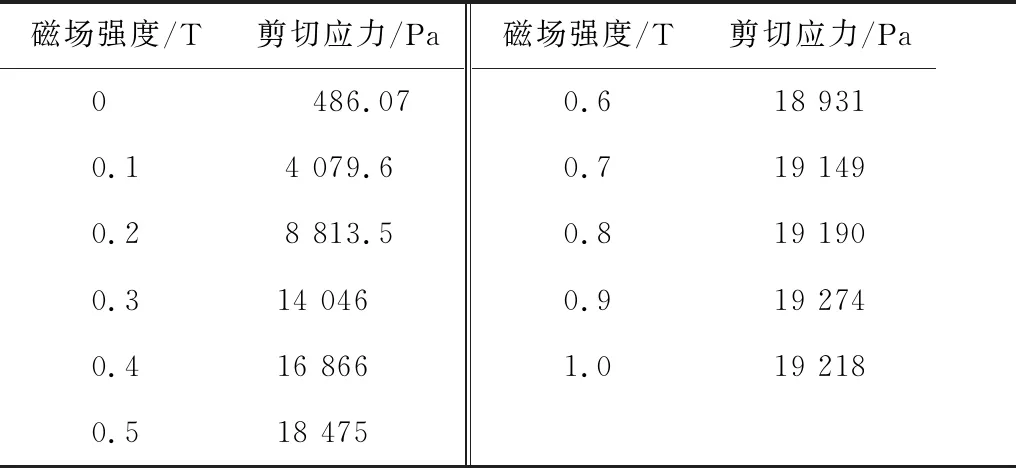
表2 磁流变液磁场-剪切应力关系Table 2 Field-shear stress relationship of magnetorheological fluid

1.2 试验加载

试验通过作动器进行位移控制，作动器的最大出力为100 kN，采用拟静态下的三角波对阻尼器进行位移加载；基座连接板和基座中心均开有圆孔，线圈导线穿过圆孔后从基座侧面引出，并与直流电源连接；试验过程中，MRD由稳压直流电源供电，且MRD 4个线圈中的电流等级保持一致，电流等级从小到大依次为0、0.5、1.0、1.5、2.0、2.3、2.6 A，在每个电流等级下，均采用图2所示的加载制度对MRD进行加载，共进行了7次加载试验，未进行重复性试验，试验装置见图3。

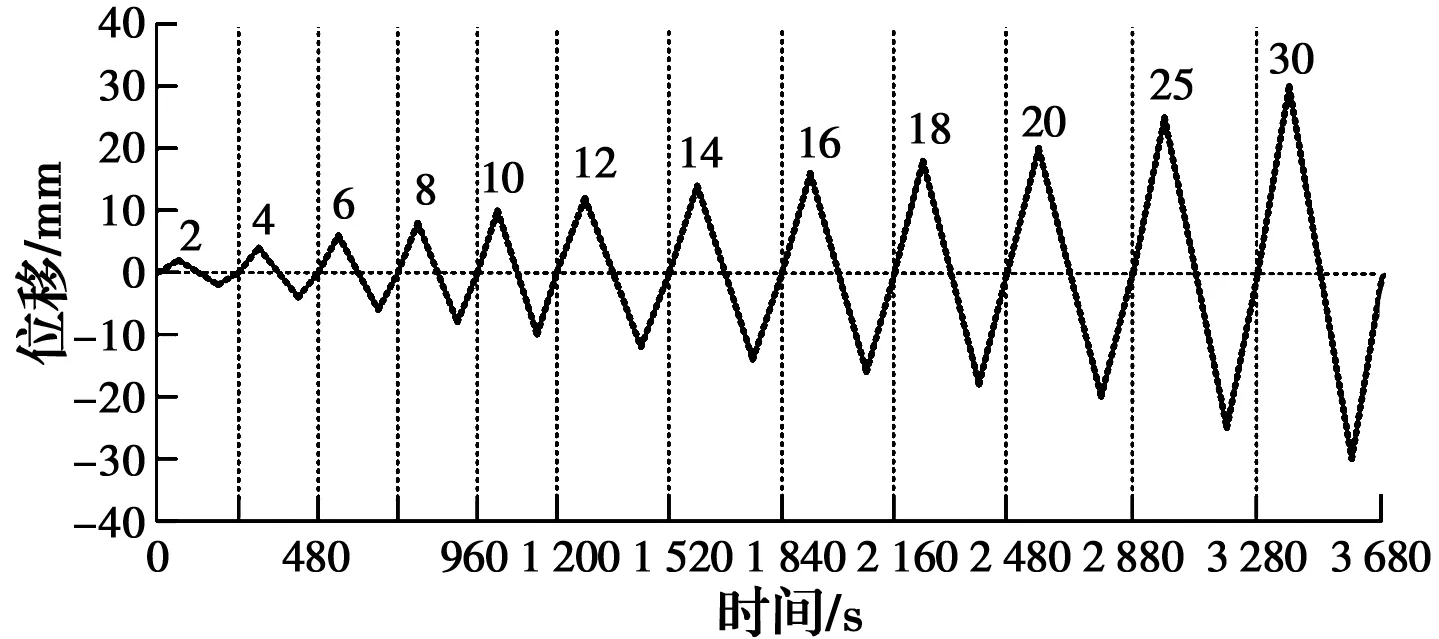
图2 阻尼器拟静态加载制度Fig.2 Quasi-static loading system of dampers

图3 阻尼器试验照片Fig.3 Test photo of MRD

2 试验结果分析

试验通过改变加载电流、阻尼器位移和加载时间，测得阻尼器在不同工况下的试验数据，通过MATLAB软件绘制，得到相关的阻尼力-位移曲线。由于图2中MRD试验的最小、最大加载速度分别为0.03、0.33 mm/s，与之对应的阻尼间隙处磁流变液的剪切速率在该剪切速率范围内，磁流变液的剪切应力相差极小，因此，在MRD试验结果分析中忽略速率的影响。

2.1 力学性能随位移幅值的变化规律

MRD在电流为0、1.5、2.6 A时，不同位移幅值下的试验结果分别如图4、图5和图6所示。

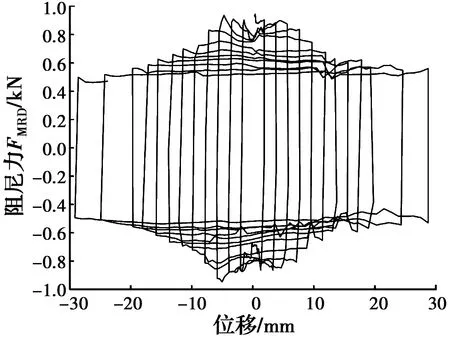
图4 不同位移幅值阻尼器试验曲线(0 A)Fig.4 Test curves of MRD with different displacement amplitude (0 A)

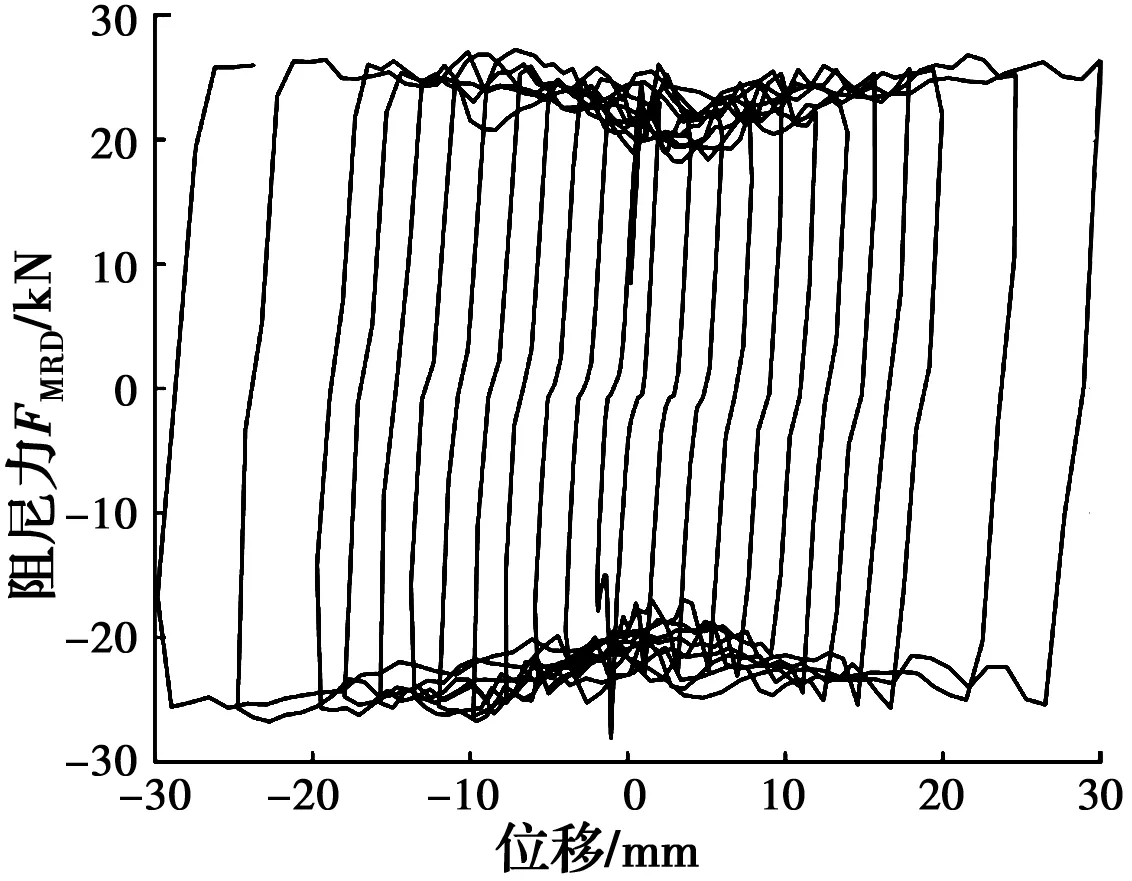
图5 不同位移幅值阻尼器试验曲线(1.5 A)Fig.5 Test curves of MRD with different displacement amplitude (1.5 A)

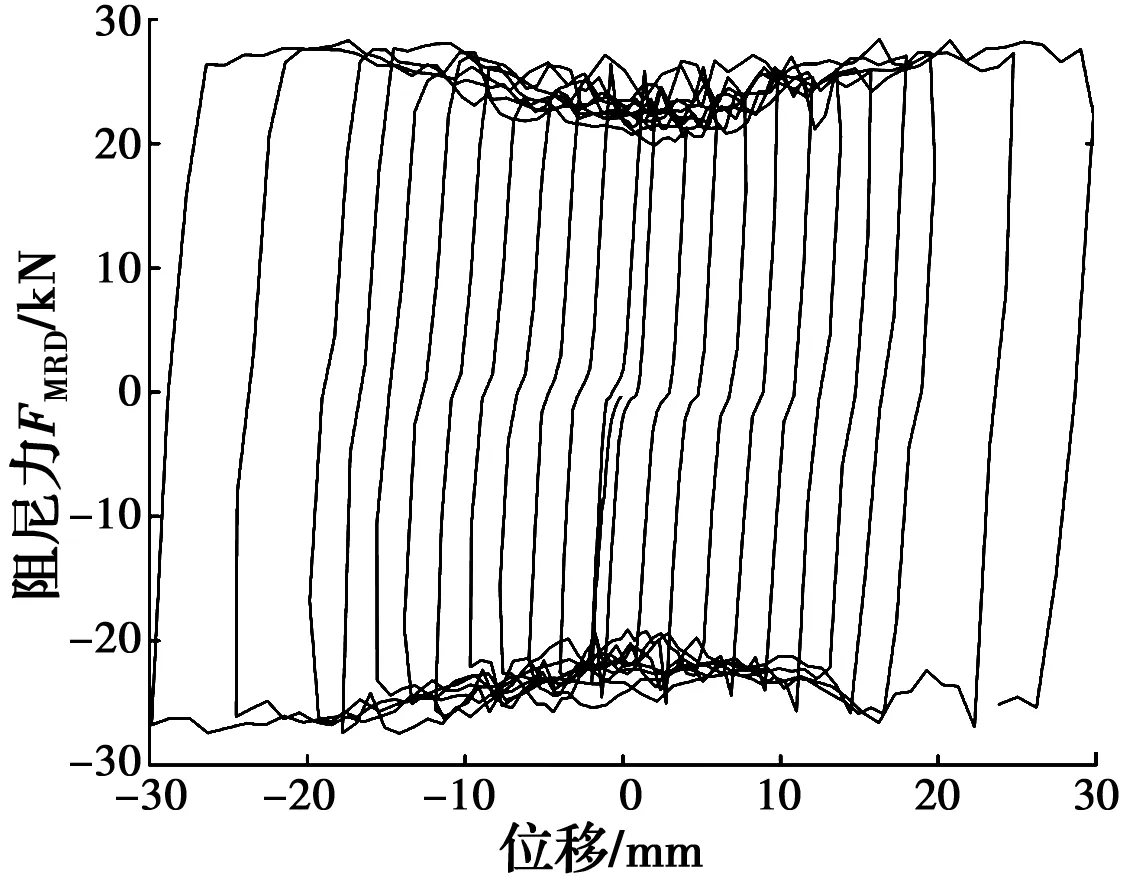
图6 不同位移幅值阻尼器试验曲线(2.6 A)Fig.6 Test curves of MRD with different displacement amplitude (2.6 A)

从图4可以看出，当MRD通电电流为0 A时，在MRD位移幅值较小时，阻尼器所提供的阻尼力值约为0.8 kN。随着MRD位移幅值的增加，MRD所提供的阻尼力逐渐降低。当MRD位移幅值为30 mm时，MRD所提供的阻尼力值约为0.5 kN。此时，MRD在较小位移幅值下阻尼力较大，而在较大位移幅值时阻尼力较小。

从图5、图6可以看出，随着MRD通电电流增加，阻尼器所提供的阻尼力也随之增加。在通电的情况下，当位移幅值较小时，MRD的阻尼力也较小；随着MRD位移幅值的增加，阻尼力也会增加。此外，由图5、图6可以看出，阻尼力迅速上升至最大值后，会在一定区间内不断波动。

Spencer等[13]在Bingham模型基础上提出修正公式

(1)

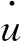
由于MRD试验为静力加载，其速度极慢，速度所产生的粘滞力很微小，可忽略不计；在低电流时，磁流变液本身剪切强度低，剪切力与挤压力也较小。此时，MRD内部摩擦力占主导地位。

摩擦力主要由活塞杆与密封圈(MRD采用O型圈密封)间相对滑动提供，摩擦力大小的变化可分为两个阶段：启动阶段活塞杆开始运动，摩擦力逐渐增大，直到达到O型圈启动摩擦力，由于在达到相对滑动前，O型圈会产生预位移，密封圈自身产生变形，所提供摩擦力较最大静摩擦力更大；之后为滑动阶段，此时活塞杆开始稳定运动，O型圈处于滑动状态，预位移得到释放，O型圈与摩擦杆之间的摩擦力趋于稳定，此时为滑动摩擦，摩擦力比最大静摩擦力要小。在MRD位移幅值较小时，阻尼器活塞的运动速度极慢，密封圈与活塞杆之间一直处于静摩擦-滑动摩擦-静摩擦不断交替的状态[14]，此时的摩擦力以静摩擦为主，摩擦力较大；在MRD位移幅值增加后，阻尼器活塞运动速度变快，密封圈与活塞杆之间稳定处于动摩擦状态，摩擦力较小。因此，在低电流时，摩擦力在阻尼力中处于主导地位，出现了小位移幅值下阻尼力较大而在大位移幅值时阻尼力较小的现象。

由式(1)可知，阻尼力部分包括挤压力Fn，而Fn与活塞移动位移成正比[15]。当阻尼器线圈通电流后，磁流变液抗压屈服强度迅速增加，此时，随着活塞移动位移的增加，挤压力也随之增加，进而导致阻尼力随着位移的增加而增加。

2.2 力学性能随电流的变化规律

不同电流下阻尼器的工作状况如图7和图8所示。当电流较小时，MRD所提供的阻尼力也较小；随着电流的增加，阻尼力也在不断增加；电流达到1.5 A后，阻尼力增加不再明显，说明MRD已经达到磁饱和状态。

图7 不同电流阻尼器试验曲线(16 mm)Fig.7 Test curves of MRD with different current (16 mm)

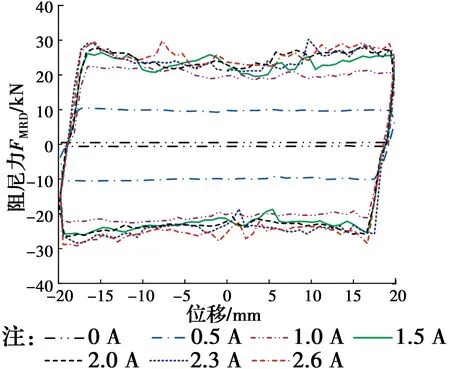
图8 不同电流阻尼器试验曲线(20 mm)Fig.8 Test curves of MRD with different current (20 mm)

2.3 阻尼力波动现象成因分析

试验采用剪切阀式阻尼器，由式(1)可知，在线圈通上一定电流后，磁流变液剪切力将成为阻尼力的主要部分。

由阻尼力的试验曲线可以看出，在MRD活塞杆的运动过程中，阻尼力没有稳定地保持在某一数值上，而是在某一区间内上下波动。

这种现象出现的原因是：如图9(a)所示，磁流变液中的磁性粒子在磁场的作用下整齐排列成链[16]，在活塞与缸体产生相对滑动时，阻尼通道中的磁流变液层间也会产生相对滑动，且随着剪切速率增加，颗粒链的倾斜角也随之增加，如图9(b)所示。在外界磁场和剪切作用的共同作用下，颗粒链将不断断裂重组，直至达到动态平衡状态[17]。由于磁流变液并非完全匀质，且拟静力加载下，剪切速率低，加载时间长，磁性粒子间的动态平衡无法保持完全稳定，随着活塞运动，打乱、破坏的磁性粒子链数量也在变化。因此，在磁性粒子链不断被打乱、重组的过程中，阻尼力也在小范围内不断波动。

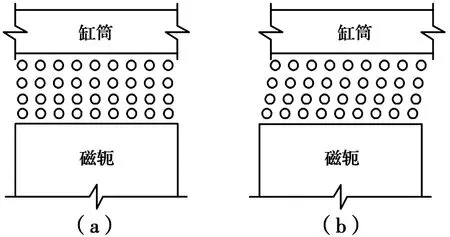
图9 磁性粒子在剪切作用下的结构演化Fig.9 Structural evolution of magnetic particles under shear

3 力学模型及参数识别

3.1 阻尼器计算模型

Fn=ku

(2)

因此，阻尼力计算公式可简化为式(3)。

FMRD=Fτ+Ff+ku

(3)

3.2 计算模型参数识别

首先确定Ff。在电流为0 A时，无外加磁场，磁流变液呈现低粘度的牛顿流体特性，此时，磁流变液剪切力Fτ和挤压力Fn均为0，MRD的阻尼力由摩擦力Ff提供。由此可得出，在各循环时，MRD摩擦力Ff的大小如表3所示。

表3 参数Ff识别结果Table 3 Identification results of parameter Ff

根据Ff识别结果，利用最小二乘法对Ff进行拟合，得到Ff的拟合公式

Ff=0.893 4e-0.021 57u

(4)

在拟静态加载下，加载速度极低，MRD剪切阻尼力Fτ的大小只与磁流变液剪切屈服强度有关，因此，在相同电流下，MRD剪切阻尼力Fτ不变。

将求得的摩擦力及不同工况下试验结果带入式(3)中，通过非线性拟合，可得到不同电流下的系数k，以及不同加载电流下MRD的剪切阻尼力Fτ，如表4、表5所示。

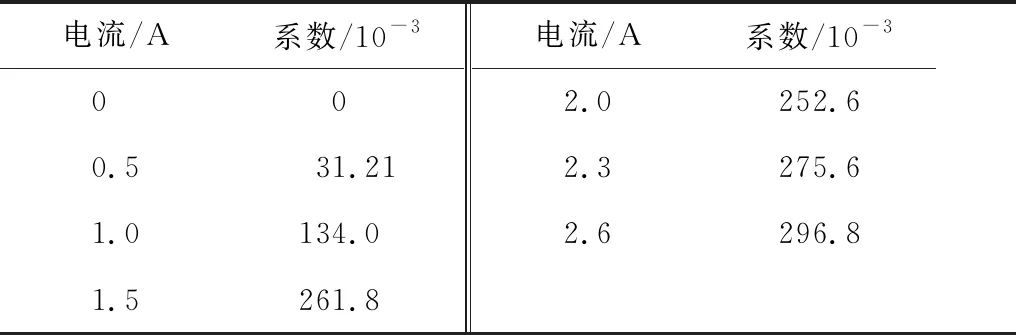
表4 参数k识别结果Table 4 Identification results of parameter k

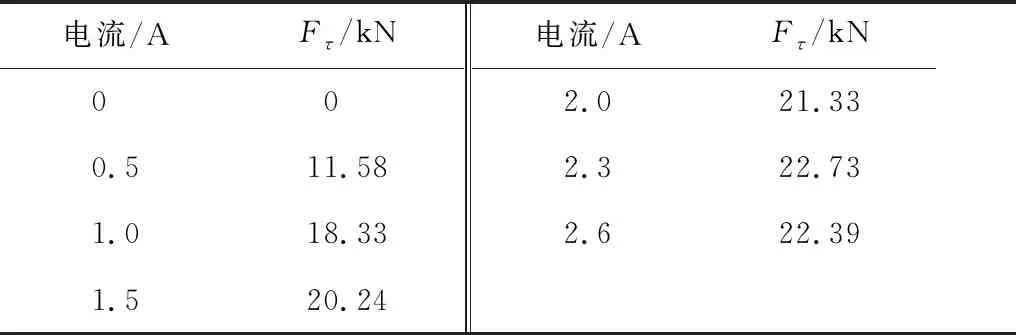
表5 参数Fτ识别结果

由于Fτ是MRD在不同磁感应强度下的屈服应力，与MRD的位移幅值和激励频率无关，只与电流强度有关。Fn是MRD在不同磁感应强度下的挤压应力，只与磁场强度以及活塞与筒壁距离有关，式(2)中，u为活塞移动位移，而磁场强度与电流强度正相关，故k为与电流强度有关的系数。

从图10、图11可以看出，Fτ与k随电流增加呈指数关系，故将模型参数表示为[18]

Fτ=Fτ0-Fτ0e-aI

(5)

k=k0-k0e-bI

(6)

采用非线性最小二乘法，根据式(5)、式(6)对Fτ和k进行非线性拟合，可得式中各参数值分别为：Fτ0=23.03、a=1.464、k0=561.4、b=0.304 1。图10、图11分别为参数Fτ和k的试验值和拟合值之间的对比。以图10为例，在电流分别为0、0.5、1.0、1.5、2.0、2.3、2.6 A时，试验测得Fτ分别为0、11.58、18.33、20.24、21.33、22.73、22.39 kN，相应电流下的拟合值为0、11.95、17.70、20.47、21.79、22.23、22.51 kN，试验值和拟合值非常接近。

3.3 模型对比验证

为了验证模型精度，将得到的模型结果与试验所得滞回曲线进行对比，如图12、图13所示。同时，通过试验数据中实测位移计算各数据点对应的模型值，与实测的阻尼力进行比较计算，取平均值得到了相应电流下试验测得阻尼力与模型计算阻尼力的平均误差，见表6、表7。

图10 Fτ试验值和拟合值Fig.10 Testvalue and fitting value of Fτ

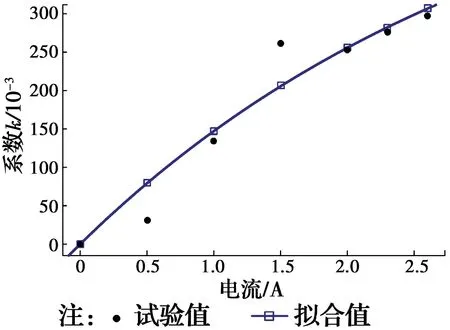
图11 系数k试验值和拟合值Fig.11 Test value and fitting value of k

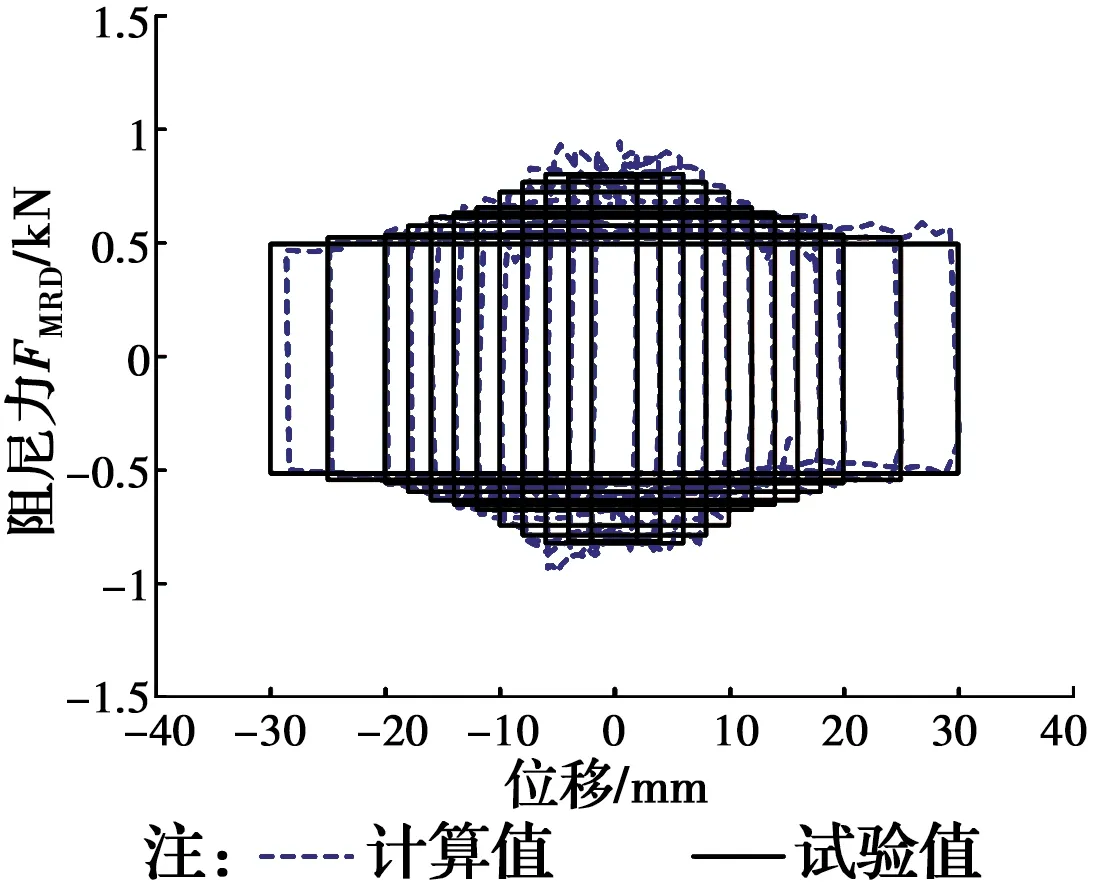
图12 模拟曲线与试验曲线对比(0 A)Fig.12 Comparison of simulation and test curves (0 A)

图13 模拟曲线与试验曲线对比(2.0 A)Fig.13 Comparison of simulation and test curves (2.0 A)

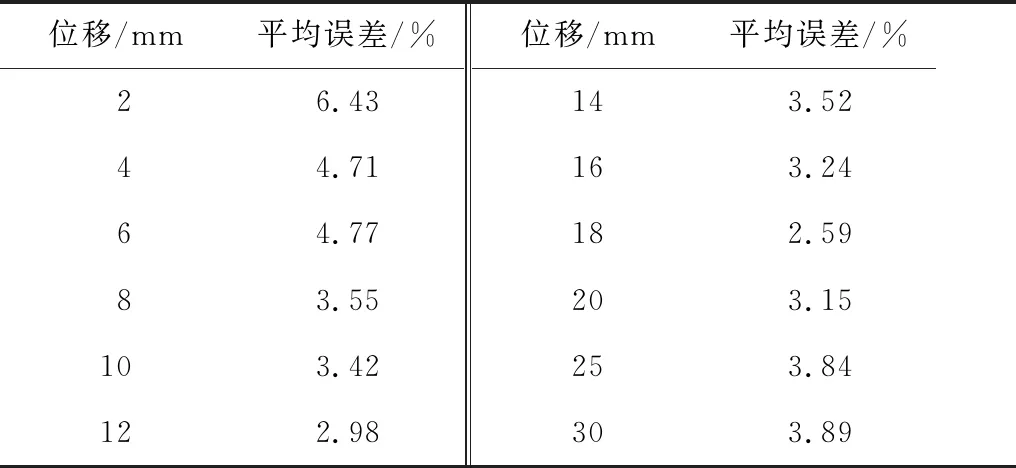
位移/mm平均误差/%026.43044.71064.77083.55103.42122.98位移/mm平均误差/%143.52163.24182.59203.15253.84303.89

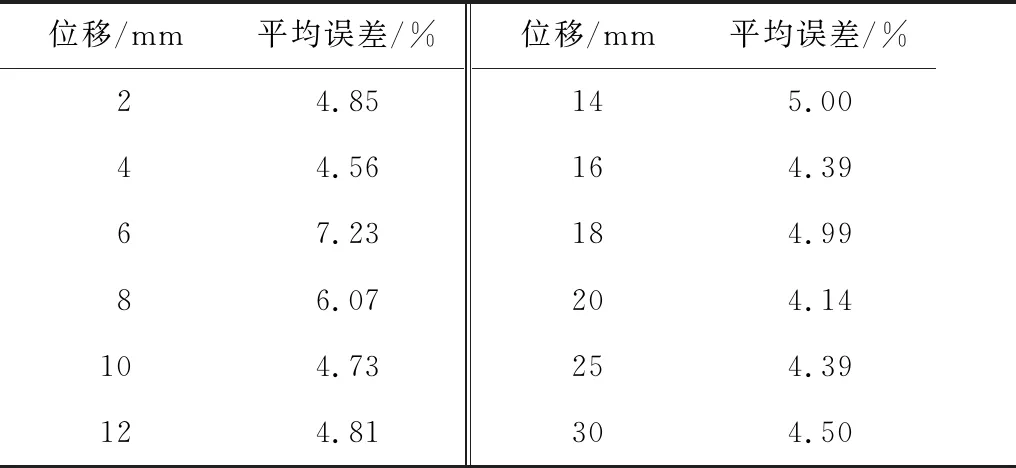
表7 实测阻尼力与模型计算阻尼力的平均误差(2.0 A)Table 7 Average error value between measured damping force and model calculated damping force(2.0 A)

从图12和图13可以看出，所得力学模型与试验结果较吻合，不仅能很好地描述出MRD在拟静态加载制度下阻尼力随电流的增加而增加的特征，也能够模拟阻尼力在不同电流下随位移幅值变化的特性，即：在无电流时，阻尼力随着位移幅值的增加而减小；在通电流时，阻尼力随着位移幅值的增加而增加。但是，该模型不能描述MRD静态试验时阻尼力随着活塞的运动而产生的上下波动情况。

从表6和表7可以看出，24组数据中共有21组误差小于等于5%；误差较大的3组数据：电流0 A时，位移幅值2 mm，电流2.0 A时，位移幅值6、8 mm，均为较小位移幅值时的工况。由于MRD在制作时无法保证磁流变液完全填满缸筒内部，会在磁流变液中存在气泡，这种情况在位移幅值较小时会导致模型误差相对较大。而在位移幅值较大的工况中，这一模型误差所造成的影响将会降低，因此，试验数据与力学模型间的误差也更小。