测距定位方程的多解性及粒子群搜索算法
2020-06-15杨文龙薛树强曲国庆王薪普王冠宇
杨文龙,薛树强,曲国庆,王薪普,王冠宇
测距定位方程的多解性及粒子群搜索算法
杨文龙1,2,薛树强2,曲国庆1,王薪普1,2,王冠宇1
(1. 山东理工大学,山东 淄博 255000;2. 中国测绘科学研究院,北京 100036)
针对用传统解算方法求解非线性测距定位方程时,其解算结果不稳定及可靠性低的问题,利用粒子群算法对测距定位方程进行求解。模拟和实测算例的结果表明,粒子群算法相较于传统解算方法能够准确、高效地搜索到多个全局最优候选解,对进一步结合实际或引入约束条件,最终获取唯一解具有一定的应用价值。
测距方程;非线性;病态方程;多解性;粒子群算法
0 引言
大地测量学科中观测模型多数为非线性模型[1-2],其中测距定位方程又是1类应用最广、最为关注的非线性观测模型。非线性平差问题,通常采用待求参数的近似值对非线性方程进行泰勒(Taylor)级数展开,并取其1阶项,使其转化为线性平差问题进行求解[3]。然而,待求参数的初值与真实值偏差较大时,会导致解算失败;当平差模型的非线性强度较大时,线性化处理甚至失效[4-5]。非线性强度的刻画,通常以模型的固有曲率和参数效应曲率作为评价指标[6-7]。
非线性观测方程的求解,通常是基于线性化处理的普通线性最小二乘法,或采用高斯-牛顿法为代表的非线性最小二乘法。大地测量平差模型病态时,线性化平差方法和高斯-牛顿法等数值解法会呈现出解的不稳定特性[8-10]。文献[2]指出,病态问题的主要特征是解的不稳定性质。文献[11]从经典测量平差理论出发,讨论了处理非线性问题的适用条件。文献[12]指出,非线性扰动主要来自于线性化过程中系数矩阵的扰动及附加的截断误差,文献[12]也讨论了非线性平差的收敛稳定性问题。文献[13]提出1种似解析非线性平差解法,该解法的基本思想源自高斯-雅克比组合平差方法,通过将超定非线性方程组转化为多个恰定方程组来进行参数求解。文献[14-15]在高斯-牛顿法的基础上,推导出了非线性的封闭式牛顿法,并对封闭式牛顿法退化为牛顿法的相关条件进行了探讨。
本文对测距定位方程解算产生多解性的原因进行解析,以控制点近似共线及近似共面2类定位构型为例,对测距定位方程多解原因进行了探讨。应用粒子群算法(particle swarm optimization, PSO)对测距定位方程进行求解,这是因为粒子群算法在求解非线性测距定位方程时,不需进行线性化处理,而且粒子群算法在解决解的多解性、稳定性及全局解搜索方面具有一定优势。最后以模拟和实测病态测距定位方程求解为例,验证了粒子群算法求解测距定位方程的优越性和可靠性。
1 测距定位方程多解性分析
大地测量学科中不适定问题是广泛存在的,其中系统的病态性更是测量平差领域中的常见问题,系统存在病态将影响参数解的稳定性,难以获取准确的参数估值和可靠的平差成果。系统病态性产生的原因涉及多方面,测距定位中系统病态性产生的原因,主要是由控制点的几何分布造成,体现在控制点与待定点组成的定位图形的设计矩阵表现出严重的复共线性。例如,当控制点近似共线或近似共面分布时,2类定位构型对待定点进行求解时,常出现多个不同解的情况产生,即由于定位图形结构而产生的病态性,使参数的求解表现为不稳定性。下面将讨论控制点近似共线和近似共面2类定位构型产生多解性的原因,图1为控制点近似共线分布示意图。
从图1中可知,控制点近似共线分布可表示为控制点分布在以圆柱体为限制的图形中,其中控制点的平面坐标(,)以圆柱体的底面圆为范围随机生成,坐标分量均匀分布在以圆柱体的高为限制的范围内,控制点的共线程度以圆柱体的半径作为评价指标,越小表示控制点的共线程度越强,反之则共线程度越弱。
控制点近似共面的分布时,控制点与待定点之间组成的定位图形如图2所示。
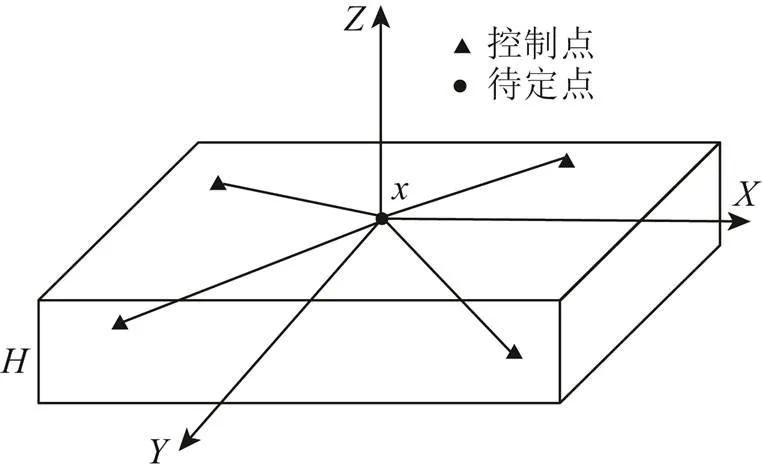
图2 控制点近似共面分布
从图2中可知,控制点近似共面分布可表示为控制点分布在以高度为限制的几何体内部,控制点的平面坐标(,)在几何体底面内均匀分布,坐标分量在高度内随机生成,控制点的共面程度以几何体的高度作为评价指标,越小表示控制点的共面程度越强,反之则共面程度越弱。
从理论上讲,仅用2个控制点的测距信息就能应用最小二乘算法对待定点坐标进行求解,然而,当控制点近似共线和近似共面时,控制点坐标分量的取值相差很小,就空间几何图形而言,其变化是微小的,是几何结构非常差的系统,因而设计矩阵是病态的;就观测信息而言,由于近似共线和近似共面时,控制点与待定点的设计矩阵不是满秩矩阵,相当于观测信息不足的情况,因而参数的求解会出现多解现象。下面从定位构型的角度,分析测距定位方程解算产生多解性的原因,图3为定位构型多解性的解析图。
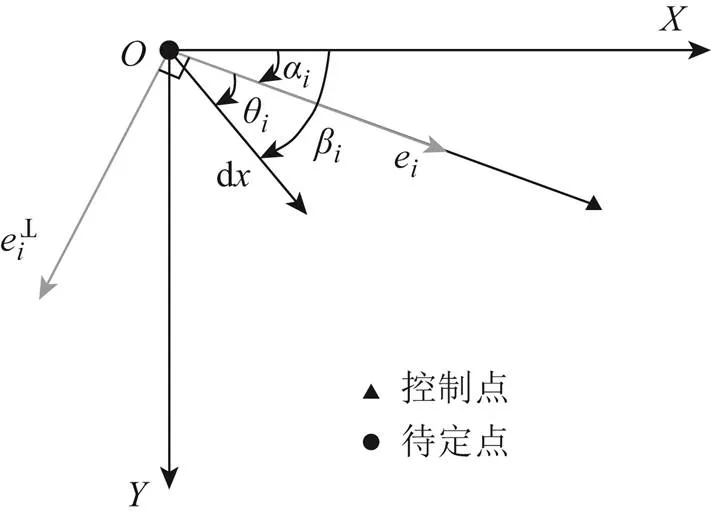
图3 定位构型多解性解析示意图
为了便于几何图解,讨论仅限于2维空间,相关结果很容易推广到3维空间。2维距离方程为





2 测距定位方程粒子群搜索解法
非线性观测方程的求解,可通过Taylor级数展开后,进行线性方程组的求解,然而当方程的非线性强度较大时,线性化所产生的误差对解算结果将产生较大的误差影响。当采用迭代算法进行参数求解时,例如高斯-牛顿算法会涉及矩阵求逆等复杂运算,待估参数初值的准确性也决定了方程组求解的成功与否,这也成为这类算法求解非线性观测方程的不足之处;此外,包括高斯-牛顿法、牛顿法等解析方法获取的解算结果通常为局部最优解,很难获得问题的全部解和全局最优解。因此,本文将启发式算法中的粒子群算法,应用于测距定位方程的求解,该算法的核心思想为种群间个体的信息交互,从而使种群个体不断优化得到问题的最优解[16]。粒子群算法具有高精度、高稳定性和全局搜索能力,计算过程中不需要进行线性化和矩阵求逆等复杂运算。图4为应用粒子群算法对最优化问题求解的流程图。

图4 粒子群算法流程图
由图4可知,应用粒子群算法的关键步骤为适应度函数的建立,对粒子的适应度进行评价,使粒子不断对自身进行优化,从而搜索到全局最优解。应用粒子群算法对待定点求解时,可将式(1)的测距定位方程转化为最优化问题的求解,即
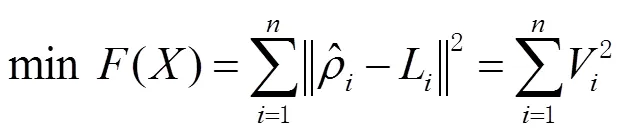

式中Fitness为粒子群算法求解测距定位方程的适应度函数。


式中:为惯性权重因子,是粒子的历史信息对速度更新产生的影响;为自身认知参数,是粒子自身历史最优值的权重系数;为社会认知参数,是粒子全局最优值的权重系数;为[0,1]区间的随机数。由式(8)可知,粒子群算法的核心思想是群体信息的传递与共享,从而使粒子在限定范围内搜索到问题的最优解,图5为粒子群算法搜索最优解过程中,粒子的更新示意图。
3 算例列举
算例1。3维测距定位中,控制点近似共线时,待定点的求解出现不稳定的态势,表现为产生多个参数解的情况。为验证这一结论,随机生成1000组近似共线的定位构型,对待定点坐标进行解算,控制点坐标范围为:坐标分量为-2~2 m;坐标分量为-2~2 m;坐标分量为-100~100 m。每组实验的控制点数目设置8个,观测距离添加0.5 m的随机误差,待定点坐标模拟值为(50 m,0 m, 50 m)。采用粒子群算法对待定点进行求解,粒子在3个坐标分量的搜索范围都为-100~100 m,移动速度范围为-2~2 m。具体的解算结果如图6和图7所示。
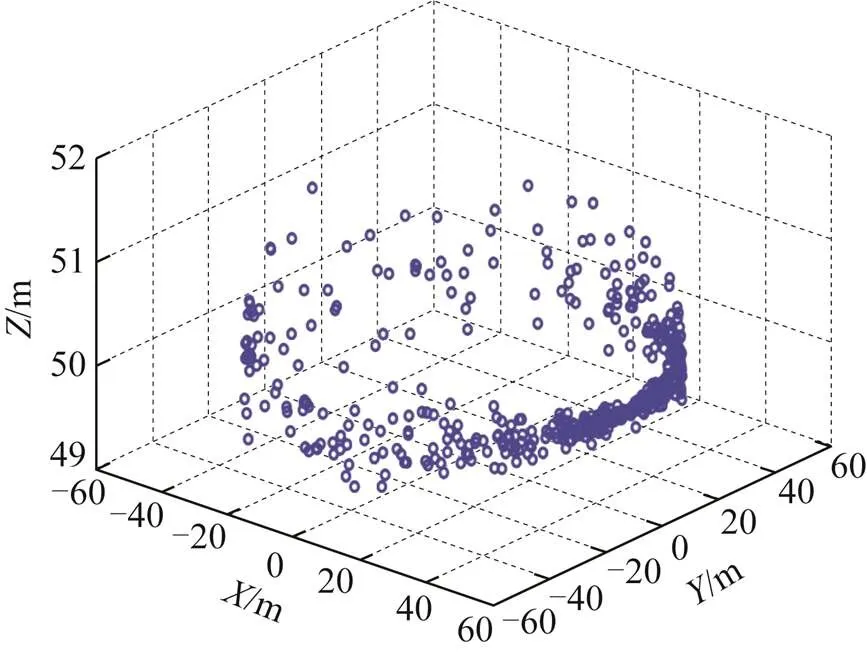
图6 控制点近似共线定位解分布

图7 控制点近似共线定位解算结果
图6和图7为应用粒子群搜索算法,对随机生成的1000组近似共线定位构型进行待定点坐标解算的结果,可知当控制点呈现近似共线分布时,待定点的解算结果分布在围绕控制点的近似圆周之上,其原因为,当控制点为近似共线分布时,控制点与待定点之间的距离计算结果与观测距离之差较小,从解算结果的残差平方和中能证实此结论,此时进行待定点的解算时会出现多解现象。
算例2。3维测距定位中,控制点近似共面时,待定点的求解出现不稳定的态势,表现为产生多个参数解的情况。为验证这一结论,随机生成1000组近似共面的定位构型控制点,对待定点坐标进行解算,控制点坐标范围为:坐标分量为-10000~ 10000 m;坐标分量为-10000~10000 m,坐标分量为-100~100 m。每组实验的控制点数目设置6个,观测距离添加0.5 m的随机误差,待定点坐标模拟值为(50 m, 0 m, 50 m)。采用粒子群算法对定位点进行求解,粒子在3个坐标分量的搜索范围都为-100~100 m,移动速度范围为-5~5 m,具体的解算结果如图8和图9所示。

图8 控制点近似共面定位解分布

图9 控制点近似共面定位解算结果
如图8和图9可知,当控制点呈现近似共面分布时,待定点的解出现在待定点与控制点平面的垂直方向上,呈现线型分布,其原因为当控制点近似共面分布时,垂直方向上存在的偏差对距离计算的影响较小,从而与观测距离之差较小,造成距离变化的不敏感而产生多解现象。

表1 控制点坐标和距离观测值 单位:m

图10 算例3的定位解分布

如图10和图11所示,当采用文献[19]中控制点近似共线的测边网算例对待定点坐标进行解算时,应用粒子群算法对待定点坐标进行1000次解算,可知当控制点近似共线时,待定点的解算结果产生多解现象呈现出近似圆形分布,与本文所得结论一致。
4 结束语
本文对控制点近似共线和控制点近似共面2类定位构性产生多解性现象的原因进行了探讨,从图形的角度进行多解现象的成因分析,发现控制点近似共线与近似共面分布时,造成多解的原因主要是由于控制点与待定点之间的距离计算结果与观测距离之差较小,从而产生多个残差平方和较小的解算结果而产生多解现象。
引入粒子群算法对测距定位方程进行解算,该算法相比于传统迭代算法不需进行线性化处理,具有高精度、高稳定性和全局搜索能力。粒子群算法为解决复杂的非线性最优化提供了全新的思路,然而算法的性能与相关参数的设置密切相关,参数的合理设置以及与其它智能算法的融合,用以提升算法的性能将会是未来研究的主要内容。
[1] 杨元喜, 张丽萍. 中国大地测量数据处理60年重要进展第一部分:函数模型和随机模型进展[J]. 地理空间信息, 2009, 7(6): 7-11.
[2] 杨元喜, 张丽萍. 中国大地测量数据处理60年重要进展第二部分:大地测量参数估计理论与方法的主要进展[J]. 地理空间信息, 2010, 8(1): 1-6.
[3] 孙振, 曲国庆, 苏晓庆, 等.测距定位模型参数估计的Landweber迭代法[J]. 测绘科学, 2019, 44(4): 15-19.
[4] STEFANIA B, SERGE G, ELISA R. A Levenberg–Marquardt method for large nonlinear least-squares problems with dynamic accuracy in functions and gradients[J]. Numerische Mathematik, 2018, 49(140): 791–825.
[5] 曲国庆, 孙振, 苏晓庆, 等. 非线性参数估计的自适应松弛正则化算法[J]. 武汉大学学报(信息科学版), 2019, 44(10): 1491-1497.
[6] 刘国林, 姜岩, 陶华学, 等. 非线性最小二乘参数平差[J]. 测绘学报, 1998, 37(3): 224-230.
[7] 王新洲. 非线性模型线性近似的容许曲率[J]. 武汉测绘科技大学学报, 1999, 24(2): 29-31.
[8] BAO Jifeng, LI Chong, SHEN Weiping, et al. Approximate Gauss–Newton methods for solving underdetermined nonlinear least squares problems[J]. Applied Numerical Mathematics, 2017, 111: 92–110.
[9] WANG Chuanyang, YU Hang, WANG Jian, et al. Bias analysis of parameter estimator based on Gauss-Newton method applied to ultra-wideband positioning[J]. Applied Sciences, 2019, 10(1): 273.
[10] 齐珂, 曲国庆, 薛树强, 等. 测距定位方程的多解性及其非线性最小二乘迭代算法[J]. 测绘通报, 2018(8): 37-40,46.
[11] TEUNISSEN P J G, KNICKMEYER E H. Nonlinearity and least-squares[J]. CISM Journal ACSGC, 1988, 42(4): 321-330.
[12] 李斐, 郝卫峰, 王文睿, 等. 非线性病态问题解算的扰动分析[J]. 测绘学报, 2011, 40(1): 9-13.
[13] AWANGE J L, GRAFAREND E W. Explicit solution of the overdetermined three-dimensional resection problem[J]. Journal of Geodesy, 2003, 76(11/12): 605-616.
[14] XUE S Q, YANG Y X, DANG Y M. A closed-form of Newton method for solving over-determined pseudo-distance equations[J]. Journal of Geodesy, 2014, 88(5): 441-448.
[15] 薛树强, 杨元喜, 党亚民. 测距定位方程非线性平差的封闭牛顿迭代公式[J]. 测绘学报, 2014, 43(8): 771-777.
[16] XIA Xuewen, XING Ying, WEI Bo, et al. A fitness-based multi-role particle swarm optimization[J]. Swarm and Evolutionary Computation, 2019, 44: 349-364.
[17] 归庆明, 张建军. 压缩型抗差估计[J]. 测绘学报, 2000, 29(3): 224-228.
Multiple solutions of distance equations and particle swarm optimization algorithm
YANG Wenlong1,2, XUE Shuqiang2, QU Guoqing1,2, WANG Xinpu1,2, WANG Guanyu1
(1. Shandong University of Technology, Zibo, Shandong 255000, China;2. Chinese Academy of Surveying and Mapping, Beijing 100036)
In view of the instability and low reliability of the traditional method to solve the nonlinear distance equation, the particle swarm optimization(PSO) algorithm is used to solve the distcace equation. The performance of particle swarm optimization is verified by simulation and practical examples. The results show that PSO can search multiple candidate solutions accurately and efficiently compared with the traditional method. It has a certain practical value for further combining the actual situation or introducing constraints to obtain the final solution of the problem.
distance observation; non-linear models; ill-conditioned equation; multiple solutions;particle swarm optimization
P228
A
2095-4999(2020)03-0121-06
杨文龙,薛树强,曲国庆,等. 测距定位方程的多解性及粒子群搜索算法[J]. 导航定位学报, 2020, 8(3): 121-126.(YANG Wenlong, XUE Shuqiang, QU Guoqing, et al. Multiple solutions of distance equations and particle swarm optimization algorithm[J]. Journal of Navigation and Positioning, 2020, 8(3): 121-126.)
10.16547/j.cnki.10-1096.20200320.
2020-03-02
国家自然科学基金资助项目(41674014,41931076);国家重点研发计划项目(2016YFB0501700)。
杨文龙(1995—),男,天津人,硕士研究生,研究方向为GNSS数据处理与应用。
曲国庆(1962—),男,山东莱阳人,博士,教授,研究方向为测量数据处理理论与方法。
