一种基于近景摄影测量的三轴气浮台连续姿态测量方法
2020-06-15张继超兰文琦金泽林杨雄丹周沛希刘建程
张继超,兰文琦,金泽林,杨雄丹,周沛希,刘建程
一种基于近景摄影测量的三轴气浮台连续姿态测量方法
张继超,兰文琦,金泽林,杨雄丹,周沛希,刘建程
(辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000)
针对3自由度气浮仿真实验平台的姿态测定中,现有测量手段对气浮台空间占用较大,导致缩减了气浮台可用负载的问题,提出1种基于近景摄影测量的3轴气浮台连续姿态测量方法:分析气浮平台姿态测定的任务需求,采用10参数模型对高精度工业相机进行标定;在气浮平台布设人工标志点,通过台体坐标系将相机坐标系下的测量值转换到真北基准下,完成气浮仿真装置姿态测量平台的搭建,实现对气浮台的连续动态测量。实验结果表明,该方法在3轴方向的重复测量误差,均优于设计的10″容差值,证明具有可行性和有效性,可以为降低航天器系统的研制风险提供参考。
3轴气浮台;近景摄影测量;标定;真北基准;姿态角测量
0 引言
随着航空航天技术的飞速发展,对航天器姿态稳定性和控制水平的要求也大幅提高。要制造更精密且结构复杂的航天器控制系统,不仅对航空航天制造技术提出了较高要求,而且对精确测定航天器在太空失重环境下的位置姿态也是一项巨大的挑战。气浮仿真实验平台能够模拟卫星本体在失重环境下的运动状态,并利用特定的测量手段,精确地测定仿真平台在任意时刻的空间姿态信息,从而对航天器系统进行评估[1-2]。
目前,根据气浮台姿态测定的需求,国内有些学者提出了基于伺服测角系统、感应同步器、倾角仪传感器等气浮台姿态测量方案,但这些系统都具有复杂的机械结构和敏感器部件,对气浮台空间占用较大,从而缩减了气浮台的可用荷载[3-4]。文献[5]提出了“陀螺加倾角传感器”(micro electro mechanical systems, MEMS)的姿态测定系统,通过采集低精度输出的MEMS陀螺仪角速度和高精度的倾角传感器数据,利用扩展卡尔曼滤波器进行角速度和角度数据处理,从而得到气浮台在3轴方向上的位姿信息。文献[6]为解决气浮台偏航轴转角难以精确测量的问题,提出通过室内星敏感器模拟仿真,进行气浮台3轴姿态角的测定方法。文献[7]通过视觉测量的方法,将光电耦合器(charge coupled device, CCD)相机安装在气浮台台面上,在台体上方布置1种非同心圆对的特征标靶,经过实验分析得出气浮台3轴姿态角、光心与平面标靶距离最大相对误差分别小于0.02 %和0.008 %。文献[8]为实现对3轴气浮台姿态的控制,尝试采用模型预测控制器的方式,以1种非线性跟踪微分器作为观测器,在控制器的配合下,0同对气浮台自由飞行与定点悬浮、矩形轨迹跟踪、圆形跟踪等运动进行仿真实验,通过与比例积分微分(proportion integration differentiation, PID)控制器进行对比,结果显示PID控制效果相对较好,但前者也显示出控制过程更加平稳直接、抗干扰能力强等优点。文献[9]提出了1种基于单目视觉的气浮台位姿测量方法,通过设计1种具有旋转、平移、缩放不变形的圆形靶标,在待识别区域内通过“行、列”扫描算法,实现靶标点圆心快速定位,并结合计算机系统下的圆心位置与视觉测量系统中的坐标转换关系,完成气浮台实际位姿的解算。
本文采用近景摄影测量方法,来解决气浮台姿态测量问题,实现了气浮台的连续动态监测。近景摄影测量方法因其具有信息容量大、非接触、操作简便、快速高效、易储存和不易受温度变化、振动等外界因素干扰的特点,已经广泛地应用到了大型工业测量领域中[10]。将近景摄影测量方法应用到3自由度气浮仿真实验平台的姿态角测量中,则是1种对气浮台姿态测量的新尝试。
本方法是在气浮台上布设人工标志点,搭建气浮台仿真装置姿态测量平台。采用高精度的相机标定方法和立方镜光学准直技术,分别标定测量气浮台姿态的相机和台体的真北基准。
1 相机标定
气浮仿真平台姿态测量的精度要求是,3轴方向的角度重复测量误差不超过10″。相机标定是影响近景摄影测量精度的主要因素之一,用标定参数修正后,能有效减弱镜头的光学畸变与相机系统误差。
1.1 相机待标定的10参数模型
为使共线方程成立,必须考虑像点坐标偏差。图像中任意点的系统性误差可以归纳为径向、偏心、像平面和内方位元素等导致的畸变误差,考虑像点系统误差的存在,共线条件方程[10]最终形式为

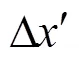
假定平面标定板在世界坐标系中的坐标为0,在2个以上位置对标定版进行采集,基于线性模型计算得出摄像机参数的1个优化解,考虑径向误差和切向误差构造目标函数,然后基于最大似然法进行非线性求解,能有效减弱镜头的光学畸变与相机系统误差的影响。采用改进的10参数模型进行相机标定,像点坐标误差方程式可由式(1)经过线性化得

其余各参数相应的系数矩阵为

c(=1,2,=1,2,…,6)为线性化后投影矩阵的相机系数,为像点的径向距离。
式(2)~式(4)统称为数字摄影相机标定的10参数模型,可根据情况对全部或部分参数进行标定。
1.2 相机标定误差分析
本文应用的高精度工业相机相机参数如表1所示。

表1 高精度相机参数
标定测量方法是使用高精度单相机,对气浮台锥形筒上的编码标志进行测量而完成的。相机测量精度取决于像点提取的精度、测量物体的大小和测量距离。
2 真北基准、相机与台体坐标间转换
为测量获取气浮台装置在真北基准下的实时姿态角,采用立方镜光学准直技术、陀螺全站仪定向寻北和同名点坐标系转换等相结合的方法,通过台体立方镜坐标系,完成动态测量相机坐标系和真北基准间关系的建立[11]。
2.1 台体坐标系与真北基准间的标定
台体坐标系与真北基准标定工作有2个方面:①通过对台体立方镜的准直测量,以及各台仪器间的互瞄,来建立台体坐标系;②寻找真北基准,将真北基准引到基准立方镜上,再通过几次方位角的转折传递,来标定台体立方镜准直面法线的地理方位角。
实验采用3台LeicaTM6100A电子经纬仪和1台陀螺全站仪。为了让各台仪器间能够通视,需要对各台仪器的安放位置进行调整,实验室测量情况如图1(a)所示。利用陀螺全站仪和LeicaTM6100A电子经纬仪间的相互瞄准观测来解算2立方镜间的转角,如图1(b)所示。

图1 台体坐标与真北基准间的标定
首先通过准直测量确定准直面法线方向,采用交会法测定立方镜中心点坐标;其次由仪器间的互瞄测量,得到各仪器设站位置点的空间坐标;最后得到立方镜中心点坐标和2台准直经纬仪所在点的坐标。以立方镜中心为原点,通过3个点确定台体立方镜坐标系的轴和轴,再由右手准则得到轴,最后测出台体立方镜准直面法线的地理方位角,即为立方镜坐标系轴的地理方位角,由此便建立了台体坐标系与真北基准之间的联系。
2.2 相机坐标系与台体坐标系间的标定
相机坐标系与台体坐标系之间的标定主要通过公共点的转换来实现。分别使用标定相机和全站仪测量台体上的标志点,获取同名标志点在标定相机坐标系和台体坐标系下的坐标数据,经过计算得到2坐标系之间的转换参数(如表2所示)。

表2 单相机与标定相机间的转换参数
由此建立动态测量相机坐标与标定相机坐标、标定相机坐标与台体坐标之间的转换关系,又因标定相机坐标系在前后2次转换中保持不变,故动态测量相机坐标系下的测量成果在经过2次坐标间的转换后,得到台体坐标系下的测量值,并且台体坐标在此之前经过与真北基准之间的标定,最终将台体坐标系下的值转换到真北基准下,获得气浮台真北基准下的实时姿态角。
3 实验与结果分析
3.1 相机标定实验
将标定板放置在稳定且周围无其他杂点的位置上,手持待标定相机从标定板正面、正面旋转90°、前俯、后仰、左倾斜和右倾斜角度进行拍摄;采用摄影测量系统IDPMS进行解算,经扫描、标志点提取、匹配和平差迭代,获得标志点点云(如图2所示)。

图2 4相机标定点云数据
根据上述求解的标志点坐标,采用待标定的10参数模型建立相机内部参数误差方程式,经解算得到4相机内部参数标定结果(如表3[12]所示)。
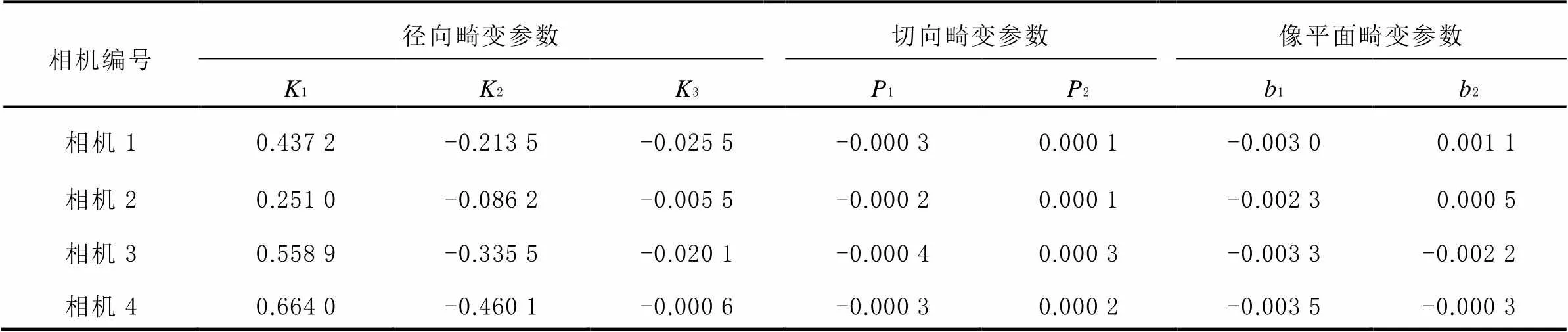
表3 测量相机内部参数标定结果
为体现相机标定对测量结果的影响,设置了7组不同畸变标定参数来进行实验。将物方点坐标计算值与高精度标定相机测量值进行对比,统计坐标差值,并用均方根(root mean square, RMS)来评定测量点精度,对比结果如表4所示。
从表4可看出:
1)镜头光学畸变对测量精度影响较大,相机使用前必须进行标定;
2)3、1和2对坐标测量结果影响较小;
3)采用10参数来修正像点系统误差是有效的。

表4 不同畸变参数标定结果
3.2 锥形测量控制网布设
实验采用模拟现场环境的方式来模拟气浮台工作,在相对稳定的环境下,采用锥形构件代替气浮台锥形筒,在锥形构件内侧粘贴直径为6 mm的编码标志块和无编码标志点,多个标志块和多个标志构成了锥形检定实验场。锥形筒内编码标志粘贴情况如图3(a)所示。首先,利用标定子系统中的高精度标定相机模块对锥形构件进行拍摄,获取锥形构件控制场图像;其次,将图像导入IDPMS中进行图像扫描、标志点识别和特征点匹配等处理,经光束法平差迭代得到控制场内各标志点坐标,最后,将其结果作为后续测量数据解算的控制点。经解算得到控制场标志点点云如图3(b)所示。

图3 气浮台锥形控制场与标志点点云
3.3 理论测量精度
使用单相机后方交会对气浮台实时姿态角测量,设计相机的测量精度小于等于10″,即在单相机后方交会时,测量精度小于等于48.5 μm。测量误差源来自于相机及解算模型误差。
采用后方交会进行精度评定的方法为

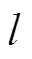
3.4 实验测量精度
实验方法为:保持锥形构件垂直朝下的初始位姿,用4台测量相机竖直向上对准锥形构件靶面;在4台相机中央架设三角支架,在支架上固定锥形构件。调节支架使构件旋转1周,转动过程中4台相机对构件进行实时拍摄,获取标志点图像后进行解算,所得点云数据及4台相机在控制场中的位置如图4(a)所示。为验证这种方法的可靠性[13-14],采用3 mm的编码块和标志点重新布设锥形构件,然后再次测量,得到点云数据如图4(b)所示。

图4 相机获得靶面标志点电云
对标志点坐标数据进行光束法平差,得到测量点的结果如表5所示。
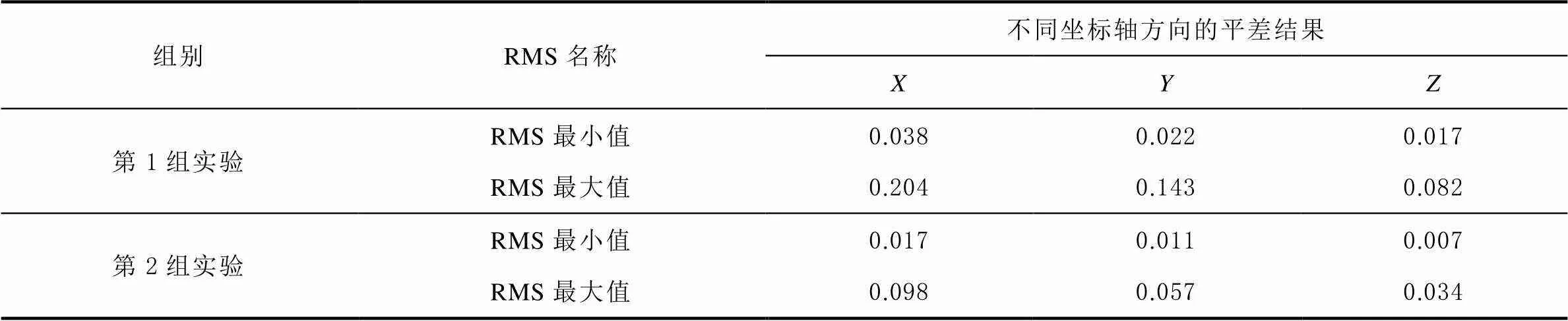
表5 测量点坐标平差结果 单位:mm
从表5可以看出,标志点坐标2次平差结果在、和3个方向上最小偏差分别为0.038、0.022和0.017以及0.017、0.011和0.007mm,相机测量及解算的点位精度高,可作为基准数据,为后续测量值作对比参考。


表6 位姿变化后标志点平差结果 单位:mm
根据前后变化的标志点坐标数据,解算模拟构件在3轴方向的角度变化,解算结果如表7所示。
从对准结果的坐标残差值来看,2次标志点对准效果相当,在3轴方向上的点位对准精度在0.02~0.05mm的理想解算精度范围,标志点坐标测量结果准确有效。
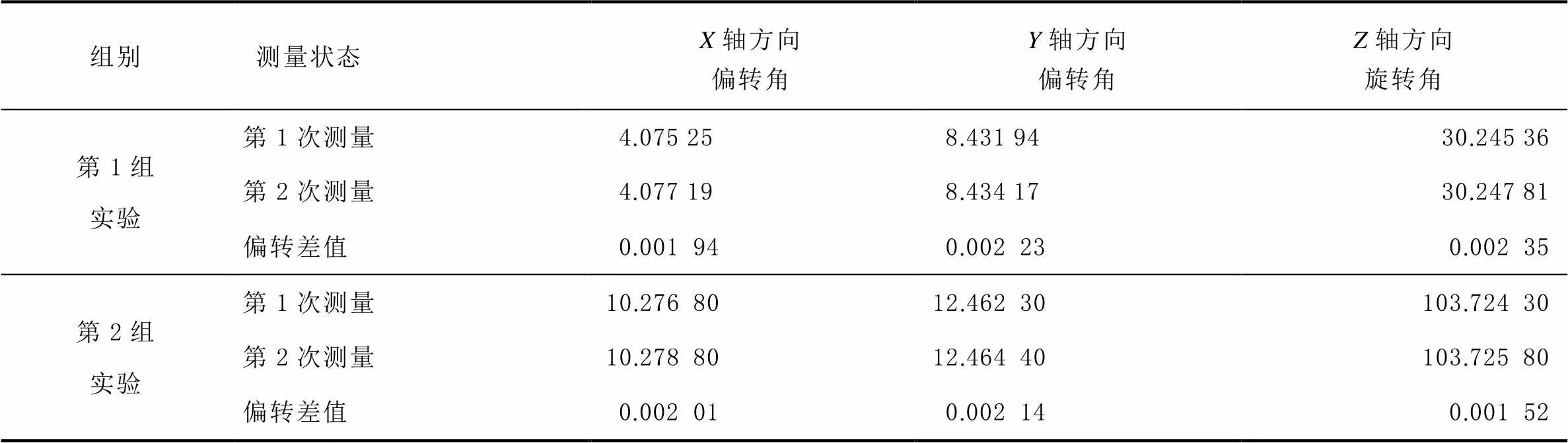
表7 模型相对初始位姿偏转值 单位:°
第1次实验测量相机在3轴方向上对模拟构件角度重复测量的误差分别为0.00194°、0.00223°和0.00235°,即差值为6.984″、8.028″和8.46″,3轴方向角度测量偏差不超过10″,满足测量精度要求。
第2次实验测量相机在3轴方向上对模拟构件角度重复测量的误差分别为0.00201°、0.00214°和0.00152°,即差值为7.236″、7.704″和5.472″,可排除测量精度效果具有的偶然性。说明采用标定的测量相机能够实现对气浮台模拟构件的精确测量,在3轴方向,姿态角的测量误差不大于10″。
4 结束语
通过分析气浮平台姿态测定的任务需求,提出采用近景摄影测量方法对气浮平台的位姿进行测量。为获得可靠的结果,首先利用10参数模型对高精度工业相机进行标定,然后通过标志点坐标解算来获取气浮仿真实验平台在3轴方向的位姿信息,经对锥形构建的实验室模拟测量,得出如下结论:
1)镜头光学畸变对测量精度影响较大,经过10参数模型标定后的相机在测量误差精度上要高出1~2个数量级,相机参数标定是必要的。
2)对动态测量相机后方交会的精度进行分析后,总结出3轴气浮台姿态角测量方案的理论精度,模拟实验表明,该测量方案在3轴方向的偏转重复误差均小于10″,验证了该测量方案的可行性。
[1] 林海奇. 三轴气浮台质量特性优化设计及其参数辨识方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[2] 潘俊帆, 康国华, 周琼峰. 三轴气浮台重心自动调整研究[J]. 航天控制, 2017, 35(2): 83-88.
[3] 李新峰, 向东, 田兴华, 等. 平面微重力模拟气浮系统的侧向力测量与处理[J]. 系统仿真学报, 2018, 30(10): 3746-3752.
[4] 徐洲洋, 肖东升. 近景摄影测量支持下的地铁盾构管片姿态测量方法及其应用[J]. 测绘通报, 2019(1): 75-78.
[5] 展浩. 基于MEMS的运动姿态参考系统的设计与研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
[6] 肖岩, 叶东, 孙兆伟.面向三轴气浮台的室内星敏感器定姿方法[J]. 哈尔滨工业大学学报, 2016, 48(10): 51-56.
[7] 邱万彬, 陆婷婷. 基于计算机视觉的三轴气浮台姿态确定[J]. 计算机测量与控制, 2015, 23(2): 554-557.
[8] 王恩友. 基于模型预测控制的气浮台运动控制研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
[9] 刘宇航, 顾营迎, 李昂, 等. 气浮实验台位姿视觉测量方法[J]. 红外与激光工程, 2017, 46(10): 195-202.
[10] 李召鑫. 基于图像处理的头盔空间位置测量[D]. 杭州: 浙江大学, 2012.
[11] 晏磊, 陈瑞, 孙岩标. 极坐标数字摄影测量理论与空间信息坐标体系初探[J]. 测绘学报, 2018, 47(6): 705-721.
[12] 楚万秀. 近景摄影测量标志点设计及信息处理研究[D]. 上海: 东华大学, 2008.
[13] 梅文胜, 胡帅朋, 李谋思, 等. 基于普通数码相机的旋转全景摄影测量方法[J]. 武汉大学学报(信息科学版), 2017, 42(2): 243-249.
[14] 黄桂平. 数字近景工业摄影测量理论、方法与应用[M]. 北京: 科学出版社, 2016.
[15] 单杰. 光束法平差简史与概要[J]. 武汉大学学报(信息科学版), 2018, 43(12): 1797-1810.
A continuous attitude measurement method of three-axis air bearing platform based on close range photogrammetry
ZHANG Jichao,LAN Wenqi,JIN Zelin,YANG Xiongdan,ZHOU Peixi,LIU Jiancheng
(School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China)
Aiming at the problem that it is reduced for the available load of the air bearing platform due to the large space occupied by the existing measurement methods in the attitude measurement of the three-axis air bearing simulation experiment platform, the paper proposed a continuous attitude measurement method of the three-axis air bearing platform based on close range photogrammetry: the task requirements of the attitude measurement of air flotation platform were analyzed, and the ten parameter model was used to calibrate the high-precise industrial camera; then the artificial mark points were set up in the air flotation platform, and the measured values under the camera calibration system were converted into the true north datum through the platform coordinate system, so as to complete the construction of the attitude measurement platform of the air flotation simulation device and realize the continuous dynamic measurement of the air flotation platform. Experimental result showed that the repeated measurement errors of the proposed method would be better than the designed 10″ tolerance value in the three-axis direction, which could provide an reference for reducing the development risk of spacecraft systems with its feasibility and effectiveness.
three-axis air bearing platform; close range photogrammetry; calibration; true north datum; attitude angle measurement
P228
A
2095-4999(2020)03-0069-07
张继超,兰文琦,金泽林,等. 一种基于近景摄影测量的三轴气浮台连续姿态测量方法[J]. 导航定位学报, 2020, 8(3): 69-75.(ZHANG Jichao, LAN Wenqi, JIN Zelin, et al. A continuous attitude measurement method of three-axis air bearing platform based on close range photogrammetry[J]. Journal of Navigation and Positioning, 2020, 8(3): 69-75.)
10.16547/j.cnki.10-1096.20200311.
2019-01-09
张继超(1975—),男,内蒙古赤峰人,博士,副教授,研究方向为遥感数据处理与应用。
金泽林(1996—),男,辽宁抚顺人,硕士研究生,研究方向为近景摄影测量和工程测量。
