鲁棒性的水下高精度时延估计算法

李记龙，王雪琰，翟玉爽，黄敏燕，冯海泓

鲁棒性的水下高精度时延估计算法

李记龙1，王雪琰1,2，翟玉爽1,2，黄敏燕1，冯海泓1

（1. 中国科学院声学研究所 东海研究站，上海 201815；2.中国科学院大学，北京 100032）

为进一步提高水下目标定位和导航的精度，提出1种适用于时变多途衰落信道的高精度时延估计算法，包括2种核心算法：高精度时延估计算法，以广义互相关算法为基础，对相关峰包络做样条插值，在降低计算量的同时，实现时延的高精度估计；鲁棒性相关包络检测算法，在相关峰包络比特征参数的基础上，引入短时能量比和子带能量比2个特征参数，在保证相同检测概率的前提下，大大降低虚警概率。实验结果证明，该算法的计算量小、性能可靠、测时精度较高。

水声定位；时延估计；短时能量比；子带能量比

0 引言

时延估计是目标定位跟踪系统的关键技术，自20世纪80年代文献[1-2]提出广义相关法以来，时延估计已成为广泛研究的课题。声波在海洋中具有最佳的远距离传播性能，是海洋环境中信息传播的主要载体。水声信道是典型的快速时变信道，不仅表现为多普勒频移严重、可用带宽窄和复杂多变的强多径干扰[3]，同时还受到海洋环境背景噪声和各类航行器噪声的干扰，这极大地降低了时延估计的精度和可靠性。

从接收机的基阵阵元个数区分，时延估计算法分为单阵元时延估计算法和阵列信号时延估计算法。单阵元时延估计算法通常应用于长基线定位导航系统，以广义互相关算法[1-2]和有限脉冲响应（finite impulse response, FIR）时延估计算法[4-6]为基础，通过计算接收信号的载波相位，估计系统的时延；阵列信号时延估计算法应用于短基线和超短基线定位导航系统，主要包括波束形成算法和特征子空间分解算法[7-10]。文献[11]的算法是阵列信号时延估计的经典算法，通过将信号空间分为期望信号子空间和干扰或噪声子空间，抑制多途干扰信号和噪声的干扰，实现了高精度的时延估计。文献[12]对多输入多输出(multiple-input multiple-output, MIMO）系统的时延估计算法进行了深入研究，在理论分析时延估计算法的基础上，给出了时延估计的克拉美-罗界（Cramer-Rao bounds）。

在水声信号定位算法中，通常假设信号是零均值平稳非高斯过程, 噪声是零均值平稳高斯过程。在低信噪比的信道中，除了采用阵列信号处理的算法提高信噪比以外，广义互相关法[2]、双谱法[13-15]或者高阶累积量[16]等改进算法也大大提高了时延的估计精度，同时系统的鲁棒性较好，性能稳定。

在水声信道中，广义互相关算法的匹配滤波输出通常是失配的，输出的包络信号存在多峰和伪峰。通过设计发射信号的波形，研究抑制相关峰包络信号旁瓣的算法[17]；同时在时变信道中，基于已知信道的统计特性，相继提出了低计算量和高鲁棒性的时延估计检测算法[10-20]。

在低信噪比和强多途干扰的水声信道中，本文提出1种高鲁棒性的时延估计检测算法。该算法主要包括，高精度时延估计算法和高鲁棒性的相关包络检测算法：采用罗斯（Roth）滤波器对接收信号做白化预处理，根据测时精度需求，采用3次样条插值的方法，对检测到的相关峰包络信号插值；采用信号的短时能量比、子带能量比和相关峰包络比3个特征，完成线性调频信号的检测；解决接收信号中的瞬时干扰信号、白噪声，有色噪声和窄带随机噪声干扰影响，比如持续的浪花声和雨滴声等。相对于相关峰包络比单特征量检测，大大降低了虚警概率，提高了相关包络检测的鲁棒性和可靠性。本文通过引入短时能量比、子带能量比2个特征检测量，理论计算虚警概率降低系数。

1 高精度的时延估计算法

发送信号经过水下多途信道传输，接收信号可以表示为

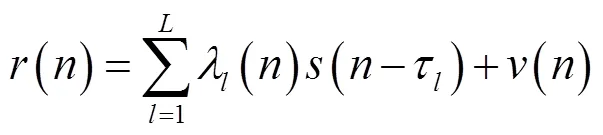
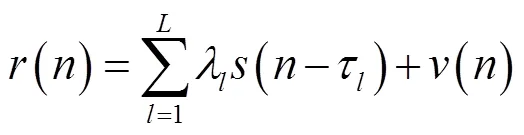
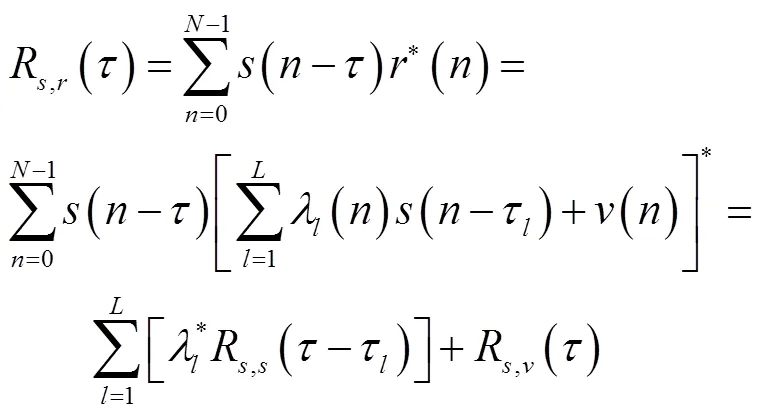
其中：

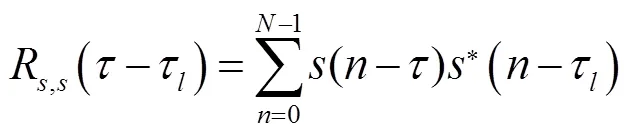
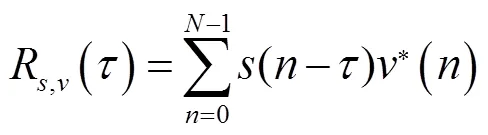
式（3）是常规的互相关时延估计算法，该算法的时延估计精度主要取决于信号的带宽和脉宽，而时延估计的准确性与接收信号的信噪比，和噪声之间的相关性有关。线性调频信号（linear frequency modulation signal, LFM）具有较大的时间带宽积；同时相位谱具有平方律特性，在脉冲压缩过程中可以获得较大的压缩比。由于匹配滤波后的输出信号对回波信号的多普勒频移不敏感，同时又具有较好的距离分辨率和径向速度分辨率，因此LFM信号广泛应用到定位导航系统。如无特殊说明，本文的发送信号主要采用LFM信号。

信号经过时变衰落信道传输后，接收到的信号中通常包括多途干扰信号、有色噪声、窄带随机噪声和谐波分量等，其中可能有明显的周期成分，噪声的干扰使得相关包络出现起伏，相关主峰变宽,甚至出现多峰现象，降低了时延估计的可靠性和精度。

广义互相关的实现流程如图1所示。

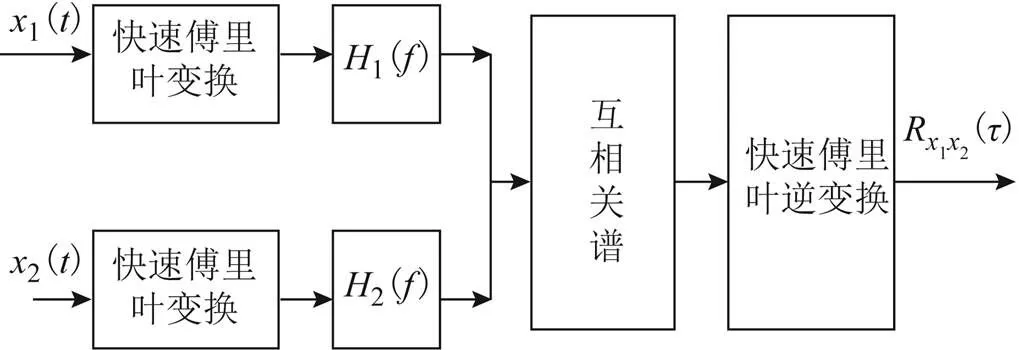
图1 广义互相关实现流程

广义互相关函数的理论计算公式为

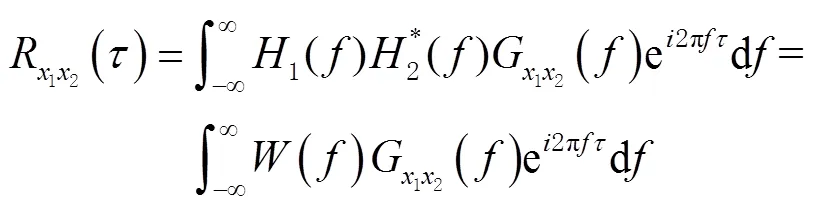
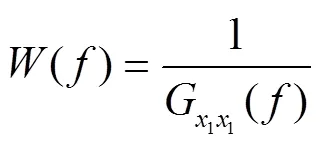
3次样条插值算法的基本思想是在满足插值条件的同时，节点划分的若干区间，除了2端的边界点外，其余内部节点具有连续的1阶和2阶导数，保证节点处光滑而且凹凸性不变，保证了插值曲线的连续性。

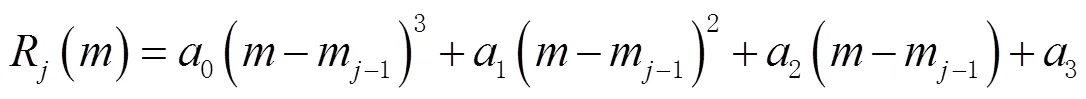
2 高鲁棒性的相关峰包络检测算法

海洋环境中有色噪声、窄带随机噪声和多途干扰信号使得相关包络函数出现振荡，相关峰的包络宽度变宽，同时相关包络函数出现多峰现象，降低了时延估计的精度。本文提出的高鲁棒性的相关峰包络检测算法应用到高背景噪声、复杂多变的水声信道中时，可以精确地检测出相关包络函数直达声信号的峰值，极大地提高了时延估计的准确性。

在远距离（>10 km）的定位系统中，定位信号的频段相对较低，而海洋环境中带有复杂的干扰噪声信号。本算法在采用信号长时间的相关峰包络比特征参数的同时，通过增加信号的短时能量比和子带能量比2个特征参量，解决了接收信号中的瞬时信号干扰问题，以及接收信号中的白噪声、有色噪声或窄带随机噪声干扰影响，比如持续的浪花声和雨滴声等；极大地降低了检测的虚警概率，增强系统检测的鲁棒性。本文提出的算法在高环境噪声的水声信道中性能良好，可靠性高，处理流程如图2所示。图2中：AD（analog-to-digital）表示模/数转换；FFT（fast Fourier transform）表示快速傅里叶变换。

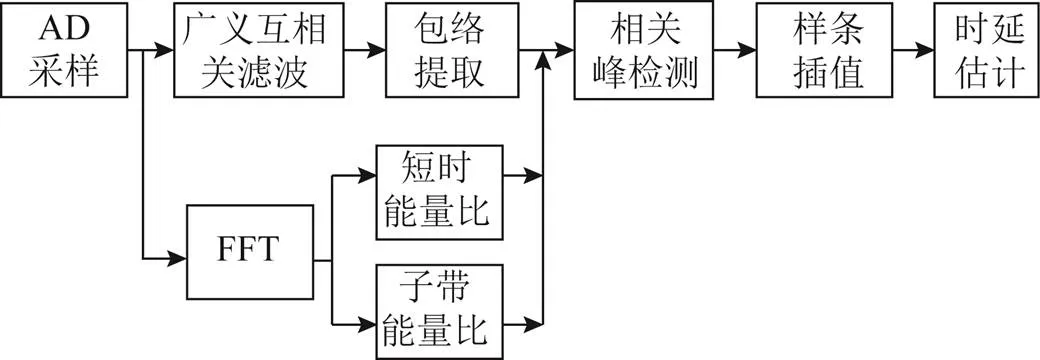
图2 时延估计算法流程

2.1 相关包络

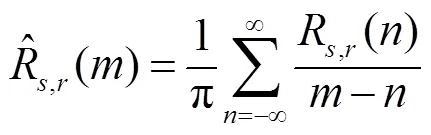
通过广义互相关函数的实部和虚部，得到广义互相关函数的包络

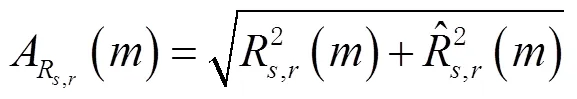
检测相关包络函数的局部极大值，对极大值做出评价和判断，完成信号相关峰包络信号的基本检测。

2.2 短时能量

接收信号分帧处理，每帧信号的长度小于定位信号脉宽的一半，实时计算接收信号的能量。通过 FFT算法，得到每帧信号的频谱为

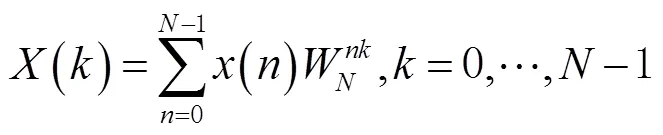
信号的短时能量是通过计算其频谱带内的能量和来获取的，其计算公式为

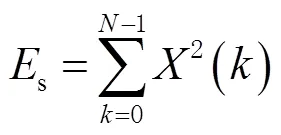
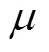
概率密度函数为

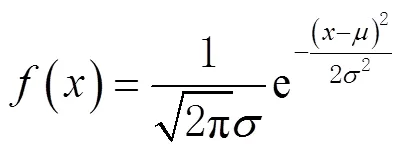
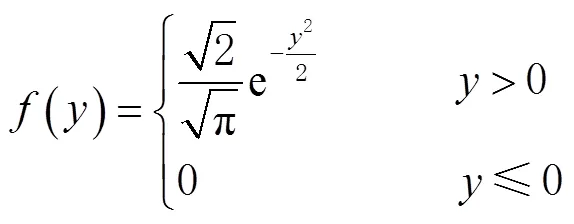
通过计算信号的短时能量，得到系统虚警概率为

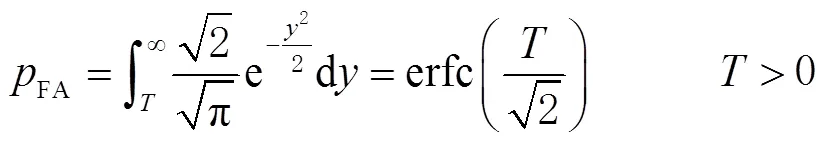
经式（14）和式（15），得到基于短时能量的虚警概率

2.3 子带能量

通过式（11）快速计算采集信号的频谱，将频谱划分不同的子带，得到每1个子带的能量为

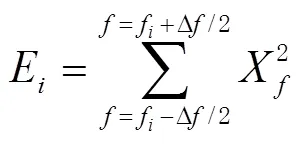
在频域中做检测，通过FFT算法，数字量化计算信号的信噪比，假设噪声信号的频点位置在1到2之间，默认每个频点的噪声是符合标准高斯分布特性的，信号的能量默认是已知的，则信号信噪比定义为

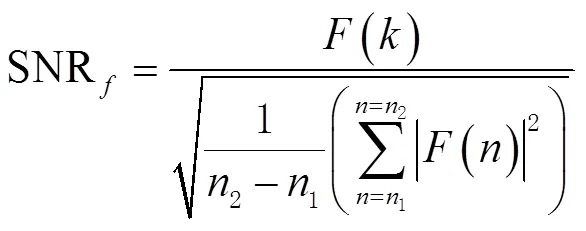
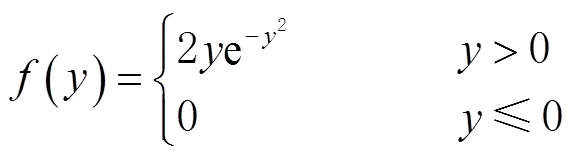
通过信号的子带能量，得到系统虚警概率为

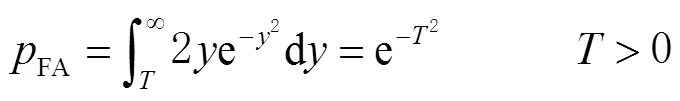
经式（19）和式（20），得到基于子带能量的虚警概率

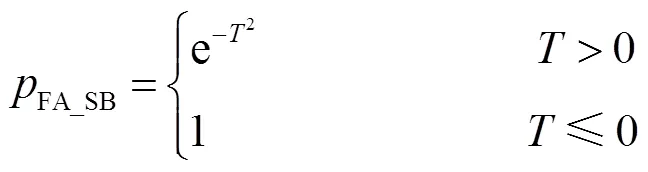
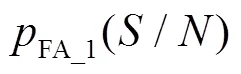
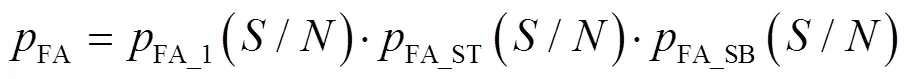
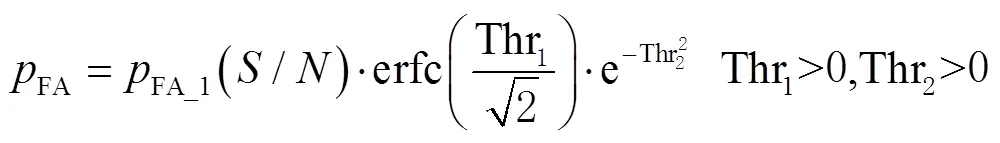
3 实验与结果分析

3.1 仿真模型

本文主要考虑了多途射线水声信道模型，模型设计如下。

根据实际应用环境，结合多途相干水声信道模型，主要考虑了能量较高的5条声线的多途影响，仿真验证了不同信噪比下的水声多途信道模型。根据信道设计模型，考虑信道的传输损失，设计了多径水声模型，其传递函数为

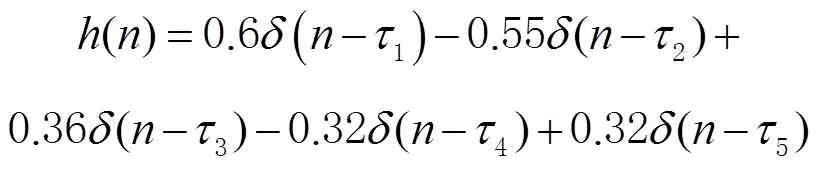
信道模型的参数如图3所示，仿真环境为通信距离5 km、水深40 m，发射换能器是全向型换能器，位于水下10 m，接收换能器位于水下15 m的水声信道。

3.2 仿真结果

在模型中，该算法主要仿真验证强多途干扰环境下，高鲁棒性的相关峰包络检测算法的性能。信噪比为30 dB，只存在多途干扰时，广义互相关输出效果如图4所示。

从图4的对比中得知，当信道存在多途干扰信号后，互相关匹配滤波的输出信号仍然存在多峰的现象。本文算法能够检测到直达声的峰值包络，实现高精度测时的功能。

仿真验证了在模型下，不同信噪比的时延估计性能（如图5所示）。

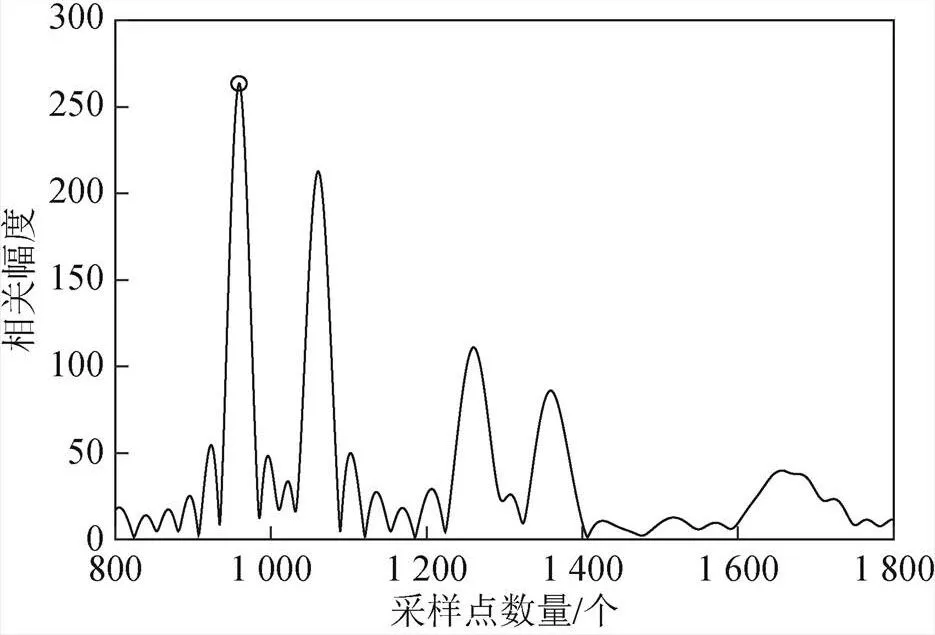
图4 信道模型下相关包络信号

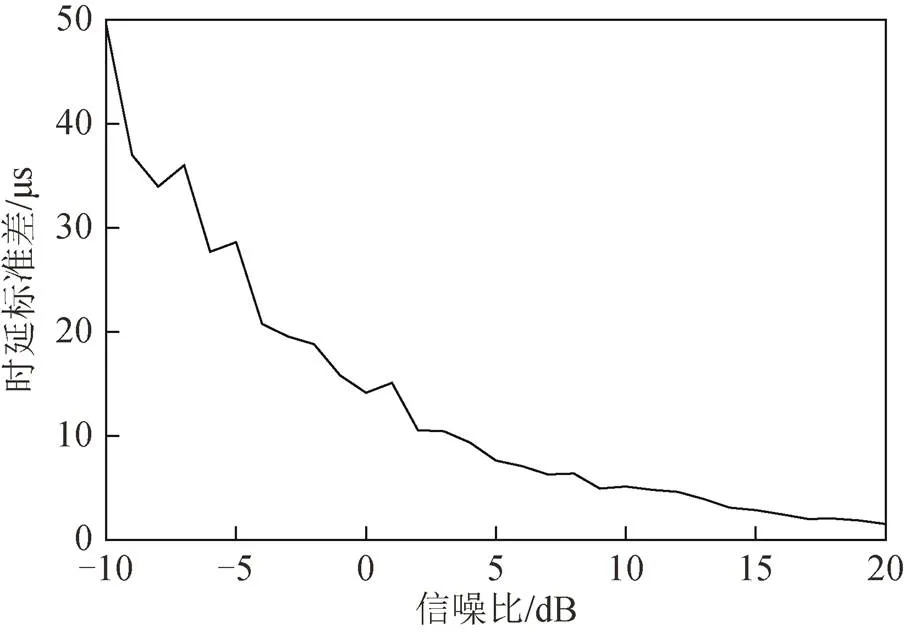
图5 时延估计算法的测时标准差

从图5中得知，在水声射线信道模型下，本文算法，在信噪比是2 dB及其以上时，测时精度优于2 μs；在信噪比是6 dB及其以上时，测时精度优于1 μs。从图7中得知，本文算法的测时标准差随着信噪比的提高而逐渐下降，可靠性越高。

3.3 湖上实验

2018年6月，在千岛湖新安江实验场做了湖上实验的验证。该实验分为2部分，第1部分是远距离的固定节点测试，第2部分的移动节点测试。

实验测试1：采用2个全向型换能器，长缆悬吊在水下10 m，发射声源级185 dB，接收灵敏度-190 dB。定位距离2.5 km，发射信号是间隔为300 ms的LFM信号脉冲串，LFM信号脉宽20 ms，带宽4~6 kHz，共测试了20组数据。接收到信号的原始波形如图6所示，相关包络信号如图7所示。

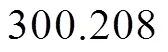
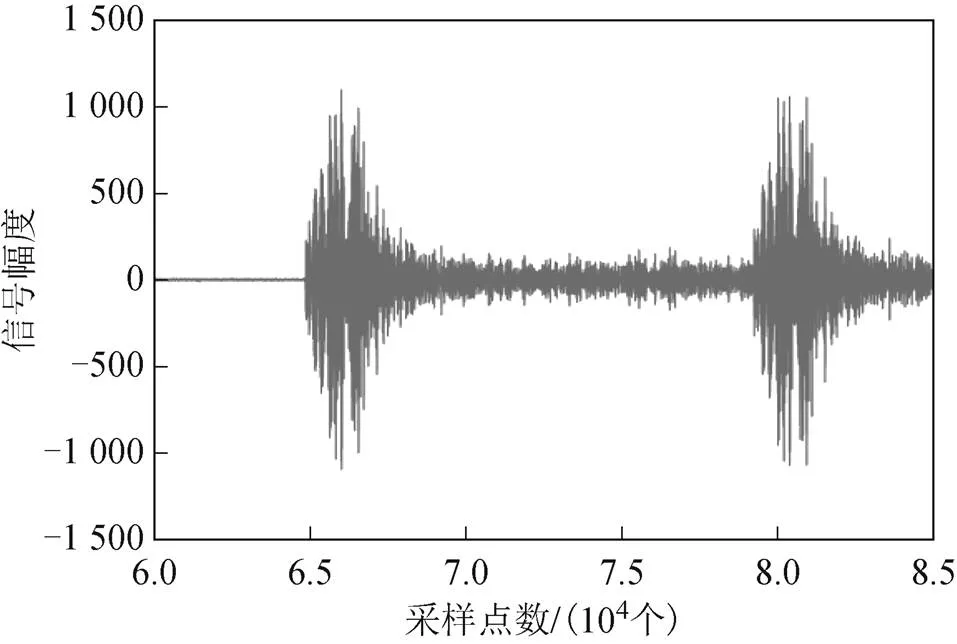
图6 接收信号原始波形

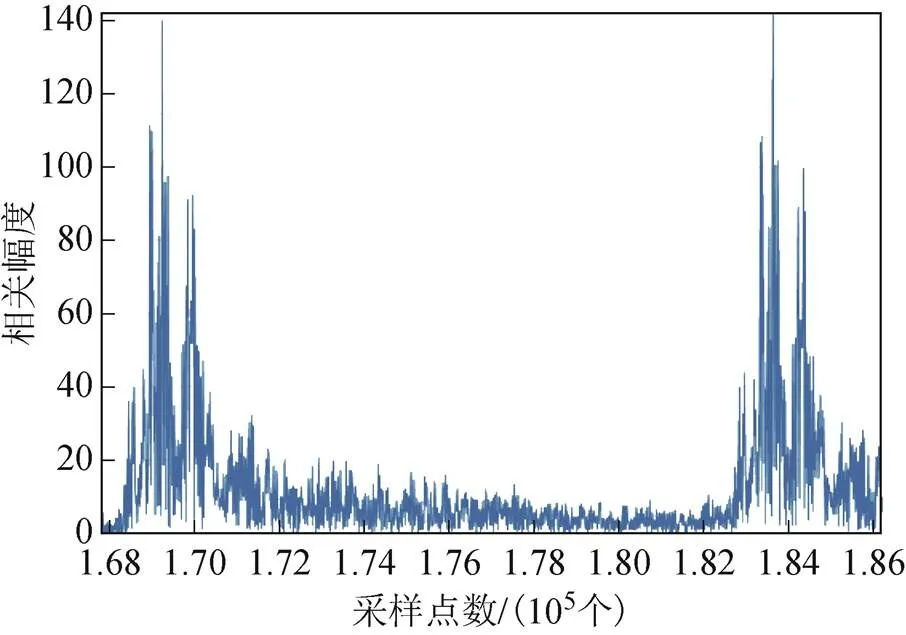
图7 广义互相关包络信号波形

实验测试2：采用2个全向型换能器，其中发射换能器长缆悬吊在水下10 m，发射声源级185 dB；接收换能器固定在水下航行器（unmanned underwater vehicle, UUV）上。UUV航速为6 kn，接收换能器的接收灵敏度-190 dB。定位距离500~1000 m，发射信号是间隔为300 ms的LFM信号脉冲串，LFM信号脉宽20 ms，带宽4~6 kHz，共测试了10组数据。

接收到的信号原始波形如图8所示，匹配滤波输出的波形如图9所示。

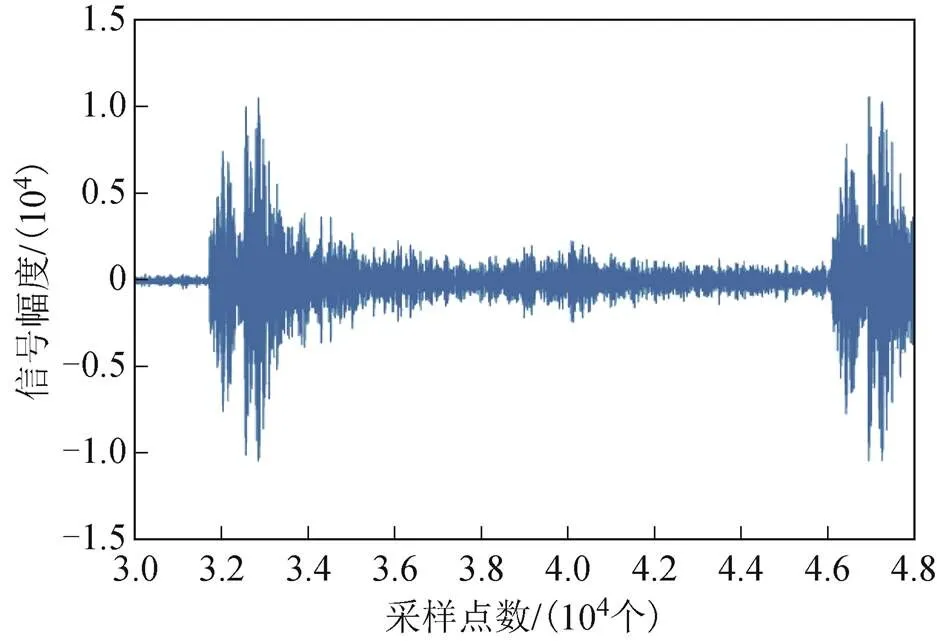
图8 接收信号原始波形

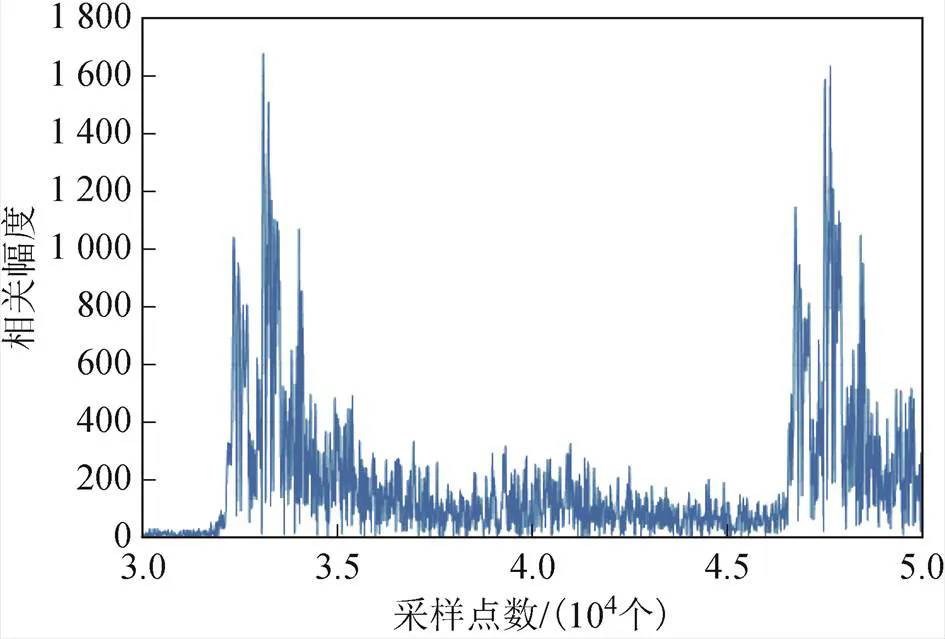
图9 广义互相关包络信号波形

测试10组信号间的测时精度，分别计算相邻2组信号的时延差，并计算均值和方差。原始信号采用48000的采样率，经过5倍样条插值后，相关包络信号的采样精度达到240000。共得到9组测时数据{300.008, 300.000, 299.996, 300.004, 300.004, 299.992, 299.992, 300.000, 299.988}，单位为ms。最终得到时延估计精度均值299.999 ms，标准差0.006 ms。在远距离测时实验中，数据处理有效率是100 %，测时精度小于1 μs。

本文从理论和仿真以及湖上实验数据处理结果等方面，分别验证了该算法测时的高精度和高可靠性，在复杂多变的时变水声信道中，准确地检测出直达声的峰值包络，采用样条插值的方法估计峰值包络的小数时延，仿真测时精度小于1 μs，湖上实验测时精度小于3 μs。在雨滴声、浪花声和螺旋桨噪声的影响下，虚警概率为0，检测概率100%。

4 结束语

[1] KNAPP C H, CARTER G C. The generalized correlation method for estimation of time delay[J]. IEEE Transactions, Acoustics, Speech and Signal Processing, 1976, 24(4): 320-327.

[2] GARTER G C. Coherence and time delay estimation[J]. Proceeding of the IEEE, 1987, 75(2): 236-255.

[3] CATIPOVIC J A. Performance limitations in underwater acoustic telemetry[J]. IEEE Journal of Oceanic Engineering, 1990, 15(3): 205-216.

[4] ANSARI R, LIU B. Efficient sampling rate alteration using recursive (IIR) digital filters[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1984, 31(6): 1366-1373.

[5] SO H C, CHING P C. Comparative study of five LMS-based adaptive time delay estimators[J]. IEEE Proceedings-Radar, Sonar and Navigation, 2001, 148(1): 9-15.

[6] MASKELL D L, WOODS G S. The discrete-time quadrature subsample estimation of delay[J]. IEEE Transactions on Instrumentation and Measurement, 2002, 51(1): 133-137.

[7] GE F X, SHEN D X, PENG Y N. Superresolution time delay estimation in multipath enviroments[J]. IEEE Transactions on Circuit and Systems-I, 2007, 54(9): 1977-1986.

[8] SAANRNISSARI H. TLS-ESPRIT in a time delay estimation[C]//The Institute of Electrical and Electronic Engineers(IEEE). Proceedings of the IEEE 47th Vehicular Technology Conference. Phoenix: IEEE, 1997: 1619-1623.

[9] BESSON O, STOICA P. Analysis of MUSIC and ESPRIT frequency estimates for sinusoidal signals with lowpass envelopes[J]. IEEE Transactions on Signal Processing, 1996, 44(1): 2359-2364.

[10] REN Q S. WILLIS A J. Extending MUSIC to single snap-shot and online direction finding applications[C]//The Institution of Engineering and Technology(IET). Proceedings of Record of IEEE International Radar Conference. Edinburgh: IET, 1997: 773-787.

[11] 王云龙, 吴瑛. 改进SSMUSIC超分辨多径时延估计算法[J]. 信号处理, 2014, 30(8): 979-986.

[12] BEKKERMAN I, TABRIKIAN J. Target detection and localization using MIMO radars and sonars[J]. IEEE Transaction on Signal Processing, 2006, 54(10): 3873-3883.

[13] NIKIAS C L, PAN R. Time delay estimation in unknown Gaussian spatially correlated noise[J]. IEEE Transactions on Acoustics Speech Signal Processing, 1988, 36(3): 291-325.

[14] ZHANG W, RAGHUVEER M R. Non-parametric bispectrum based time delay estimators for multiple sensor data[J]. IEEE Transactions on Signal Processing, 1991, 39(3): 770-774.

[15] HINIEH M J, WILSON G R. Time delay estimation using the cross bispectrum[J]. IEEE Transactions on Signal Processing, 1992, 40(1): 106-113

[16] TUGNAIT J K. Time delay estimation with unknown spatially correlated Gaussian noise[J]. IEEE Transactions on Signal Processing, 1993: 41(2): 549-558.

[17] MA N, GOH J. Ambiguity-function-based techniques to estimate DOA of broadband chirp signals[J]. IEEE Transactions on Signal Processing, 2006, 54(5): 1826-1839.

[18] 崔维嘉, 张鹏, 巴斌. 基于贝叶斯自动相关性确定的稀疏重构正交频分复用信号时延估计算法[J]. 电子与信息学报, 2019, 41(10): 2318-2324.

[19] 童峰, 许肖梅, 方世良. 一种单频水声信号多径时延估计算法[J]. 声学学报(中文版), 2008, 33(1): 64-70.

[20] 王巍, 熊瑾煜, 朱中梁. CDMA信号码片内多径时延估计算法[J]. 电子与信息学报, 2004, 26(9): 1345-1350.

A high-precise time delay estimation algorithm with robustness for underwater acoustic channel

LI Jilong1, WANG Xueyan1,2, ZHAI Yushuang1,2, HUANG Minyan1, FENG Haihong1

(1. Shanghai Acoustics Laboratory, Chinese Academy of Sciences, Shanghai 201815, China; 2.University of Chinese Academy of Sciences, Beijing 100032, China)

In order to further improve the accuracy of underwater target positioning and navigation, the paper proposed a time delay estimation algorithm with high precision and robustness for time-varying and multipath fading channels, which includes two key methods: based on generalized cross correlation algorithm, the spline interpolation was performed for the correlation peak envelope by the high-precise time delay estimate, to realize the high-precise estimation while reduce the computation; based on the features of correlation peak envelope ratio, the short-term energy ratio and sub-band energy ratio were introduced by the robust correlation envelope detection, to greatly reduce the false alarm probability while keep the same detection probability. Experimental result showed that the proposed algorithm would have small calculation, reliable performance and high accuracy of time measuring.

acoustic positioning; time delay estimation; short-term energy ratio; sub-band energy ratio

P228

A

2095-4999(2020)03-0058-07

李记龙，王雪琰，翟玉爽，等. 鲁棒性的水下高精度时延估计算法[J]. 导航定位学报, 2020, 8(3): 58-64.（LI Jilong, WANG Xueyan, ZHAI Yushuang, et al. A high-precise time delay estimation algorithm with robustness for underwater acoustic channel[J]. Journal of Navigation and Positioning, 2020, 8(3): 58-64.）

10.16547/j.cnki.10-1096.20200309.

2019-12-31

国家重点研发计划项目（2016YPB0501703）；国家自然科学基金重点项目(61531018)。

李记龙（1988—），山东德州人，博士，助理研究员，研究方向为水声定位和通信。