范数最小估计的海底大地控制点精密标校方法
2020-06-15胡致远王盼龙唐秋华周兴华周东旭
胡致远,王盼龙,唐秋华,周兴华,周东旭
范数最小估计的海底大地控制点精密标校方法
胡致远1,2,王盼龙3,唐秋华1,2,周兴华1,2,周东旭2
(1. 山东科技大学 测绘科学与工程学院,山东 青岛 266590;2. 自然资源部第一海洋研究所,山东 青岛 266061;3. 自然资源部大地测量数据处理中心,西安 710054)
针对海洋测绘水下声学定位中常用的最小二乘平差法易受粗差和系统误差影响,导致解算精度和稳定性较差的问题,提出1种水下控制点解算的方法:介绍海底大地控制点标校基本原理和方法,给出全球卫星导航系统(GNSS)和水下声学定位模型;然后选用中国科学院测量与地球物理研究所(IGG)选权迭代法和一次范数最小法,用于水下声学定位数据精密标校。实验结果表明,一次范数最小法能有效抗拒异常观测扰动,抗差能力较强,能够实现浅海海底控制点厘米级定位精度。
海底大地控制点;水下声学定位;一次范数最小法;选权迭代法
0 引言
海洋占地球表面积的71 %,对其进行调查研究和合理开发利用,对我国这样的海洋大国是必不可少的。以海洋大地控制网为代表的海洋基础测绘设施建设,是完成这些工作的先决条件,而高精度的水下声学定位技术是建设海洋大地控制网的基本保障。
1985年,斯克里普斯海洋研究所的Spiess教授首次提出利用全球定位系统(global positioning system, GPS)和声学定位系统相结合来构建海底大地控制网[1-2]。该方法利用GPS动态差分的方法求出测量船在地固坐标系下的坐标,结合声学信号测量船载换能器和水下应答器之间的传输时间,联合平差解算得到海底控制点绝对坐标。自该方法提出以来,美国、日本、欧洲等国家和地区先后开展了海底大地控制网的研究与布测[3-15],通过不断完善海洋大地测量的基础设施建设,有效地提升了海洋学科的综合实力。我国海洋大地测量基准建设,虽然较陆地相关研究发展较晚,但相关的海洋技术研究和应用却发展迅速[16]。近年来,国内学者对海洋大地测量基准建设涉及的关键技术进行了深入研究,取得了一些成果[17-20]。
高精度海底大地控制点坐标的获取,需要全球卫星导航系统(global navigation satellite system, GNSS)技术和声学定位技术相结合后,进行高精度的标校才能满足要求;但由于海洋环境复杂多变,水下的声线传播存在传播延时和声线弯曲等影响,这给水下声学测距带来较大误差,给海底大地控制点的精确标校带来困难[17-20]。本文针对声学测距结果包含大量粗差和系统误差、常用的最小二乘法易受粗差和系统误差的影响,其解算精度和稳定性较差的问题,提出基于一次范数最小法的抗差最小二乘估计,用于水下控制点的解算,并使用青岛灵山岛附近海域实验数据进行了验证。
1 GNSS/水下声学定位模型
通常海底控制点(应答器)位置精确标校是由安装在测量船底部的换能器发射出声信号,位于海底的应答器接收该声信号并给予反馈,反馈的声信号由换能器接收并记录声信号在海水中的传播时间;通过对声速的测量获取声速,声速乘以声信号单程传播时间即可获得换能器和应答器之间的距离。当观测到3个以上的距离值后,利用距离交会方法可以精确解算出海底应答器的3维坐标位置,如图1所示。
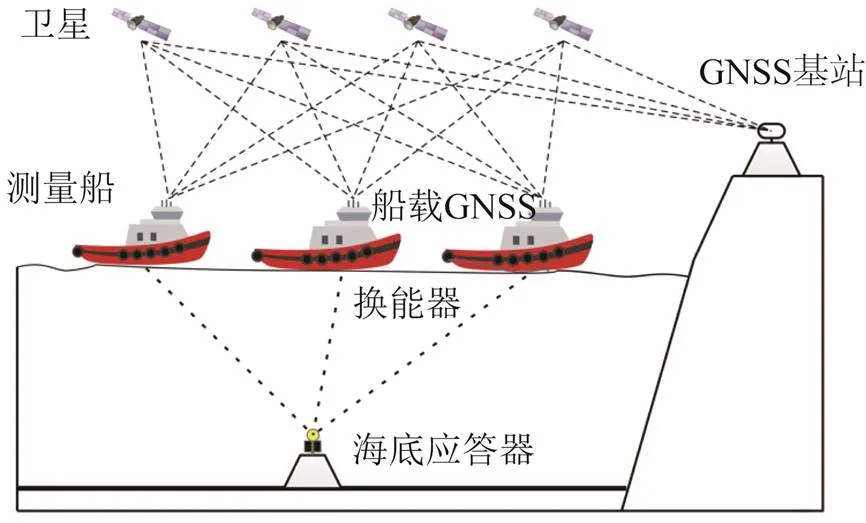
图1 海底应答器精确位置解算示意

线性化式(1)后得
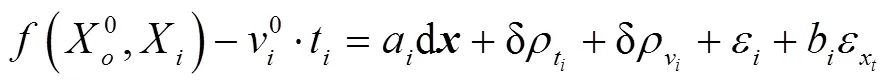
当观测历元数大于3,在不考虑系统误差影响的前提下,根据式(2)得出误差方程为
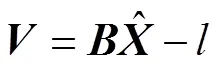
根据最小二乘推导法方程为

解得
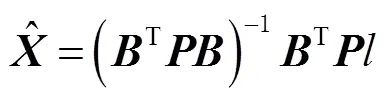

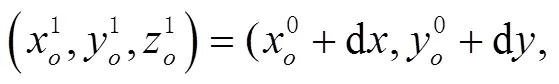

协方差阵为
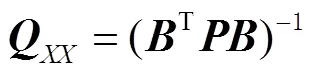
2 水下声学定位抗差估计方法
受海洋环境复杂多变的影响,水下声学观测数据存在着一定的粗差。在经典最小二乘平差中,通常假定观测值中仅含偶然误差,并且观测误差服从正态分布,由此可以根据最小二乘准则求出未知参数最优估值,并进行精度分析。这种条件下,估计的参数是最优线性无偏估计。水声观测数据中的粗差会破环最小二乘无偏估计的前提。近代测量平差中,通常有2种粗差处理方法[21-22]:将粗差归入随机模型处理。第1种方法使用3倍中误差作为限差,对数值较大的粗差处理效果好,但是难以发现数据中数值较小的粗差;第2种方法根据逐次迭代平差的结果不断修正观测值的权或方差,最终使含有粗差的观测值的权趋向于零或者方差趋向于无穷大,对较小的粗差也有很好的处理结果。
本文将常用的随机模型抗差法,即选权迭代法和一次范数最小法用于水下声学定位粗差探测。
1)IGG选权迭代法。IGG(Institute of Geodesy & Geophysics, Chinese Academy of Sciences)选权迭代法由中科院测量与地球物理研究所周江文[21]提出,其函数来源于M估计,即
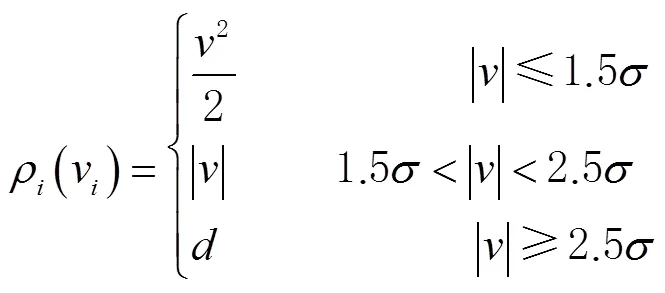

IGG选权迭代法表明:当观测值服从正态分布时,采用最小二乘估计;当观测值超出给定范围时采用降权估计,当有观测值出现明显的异常就采用淘汰法将其剔除。
自IGG选权迭代法提出以来,众多学者对其在测量数据抗差估计的应用中做了大量研究和改进。文献[22]提出采用最小二乘法(least square method, LS)估计的IGG Ⅲ方案;文献[23]提出了1种可容忍较大面积数据污染的符号约束抗差估计方法;文献[24]提出了分别采用了IGG Ⅲ方案和双因子等价权函数的抗差估计法。该抗差方法在GNSS数据处理中应用效果较好,但在水下声学定位数据处理中应用还不多见。
2)一次范数最小法。抗差估计的抗差性及有效性主要取决于初值的准确性与权函数的合理性。目前通常选取最小二乘估计的结果作为抗差估计的初值,但最小二乘估计对粗差具有不敏感性和均衡性,致使含有粗差的观测值的残差并非最大,导致选权迭代时易出现错误判断[25]。采用一次范数最小估计法,由于其有较强的稳健性,对测量数据的粗差发现有着较好的效果[26-27],能有效削弱滤波后的观测值中误差对结果的影响。
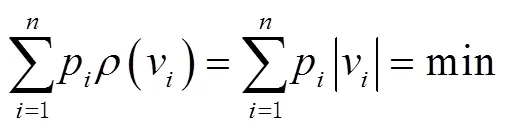
误差方程写为
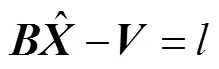

得
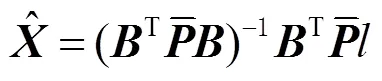
3 实验与结果分析
3.1 实验数据采集
为检验本文提出的海底控制点坐标位置标校方法的正确性,在青岛灵山岛东部海域进行海上标校实验,实验场如图2所示。该海域地势较为平坦,水下地形起伏变化不大,平均水深在20~30m之间,且海底沉积物类型为砂质粉砂,无地质灾害赋存的迹象,能够满足海底控制点布设要求。

图2 海底控制点标校实验位置
标校实验前,严格测定船载换能器、GNSS天线和惯性测量装置(inertial measurement unit, IMU)姿态传感器在船体坐标系下的坐标,将其归算至统一坐标系统下。标校过程中,测量船围绕海底应答器,进行田字走航和圆形走航测量(如图3所示),同步采集高精度船载GNSS、水下声学定位数据。
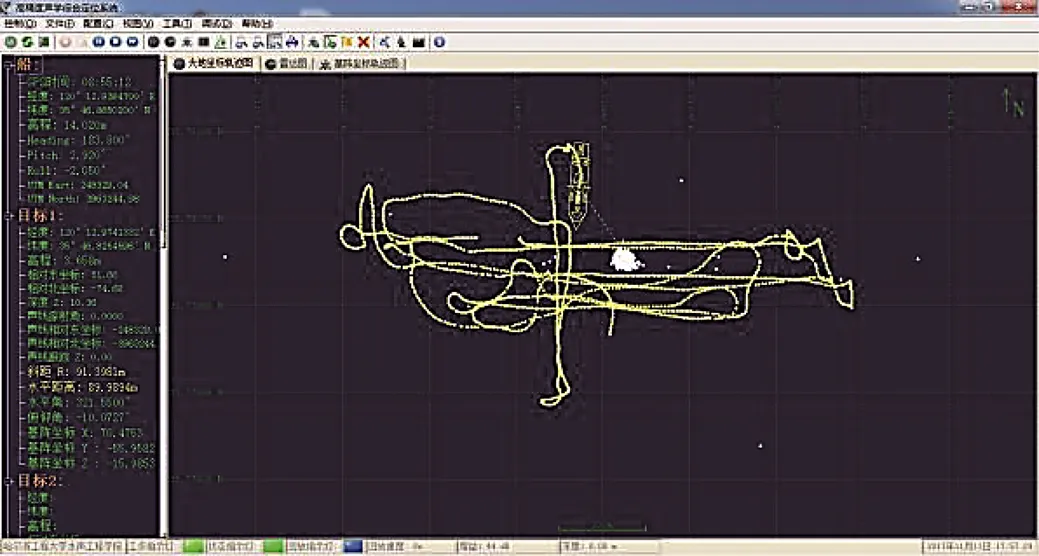
图3 海底控制点标校实验航迹
3.2 声速确定
实验海区位于青岛灵山岛周围的浅海区域,海水深度在25 m左右,通过现场实测的温、盐、深等参数计算出来的声速剖面如图4所示。
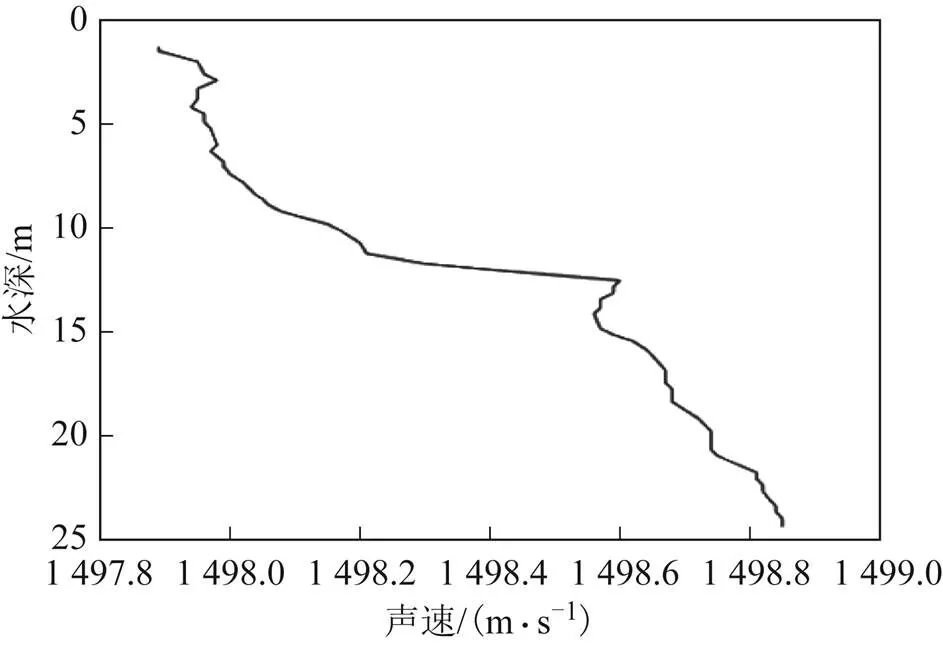
图4 标校实验海区声速剖面
有研究表明,在声速变化不超过1 m/s的水域,当声学定位入射角小于80°时,声线弯曲造成的测距误差为毫米级[28],可以用平均声速代替声线跟踪算法标校浅海海底控制点坐标。
在浅海水下定位中,求声速常用方法的有平均声速法,初始平均声速为

3.3 不同航迹组合解算结果比较
分别提取小圆、大圆和田字等3种简单图形的航迹定位数据。其中,小圆半径约为77 m(3倍水深),大圆半径约为200 m(10倍水深),田字航迹中心位于应答器正上方附近,最大边长为120 m。将3种不同形状单一航迹进行组合,形成套圆、小圆加田字、大圆加田字以及套圆加田字等4种组合航迹图形。7种航迹图形如图5所示。

图5 7种不同标校航迹
为了验证海底控制点精密标校方法与精度,设计了3种海底控制点标校解算方案。
1)方案①:利用平均声速1498.39 m/s进行最小二乘迭代解算,得海底控制点的坐标。将所有观测值的权值设为1,假设换能器到应答器的距离观测值不受系统误差影响,观测误差均由随机误差引起,声速值为1498.39 m/s。通过最小二乘迭代法解算,得到各走航航迹下应答器坐标及定位精度,其结果如表1所示。

表1 经典最小二乘法海底控制点解算结果 单位:m
由表1可知,利用平均声速进行最小二乘法坐标解算,不同航迹的海底应答器坐标解算精度都不高,尤其高程变化较大,高程精度远低于平面精度。其中:
①半径为77 m的小圆航迹标校精度最高,平面中误差为3 cm,高程方向解算精度为6 cm;原因主要是,小圆航迹在水平方向上近似对称,利用最小二乘法解算时,可以消除或减弱平面方向上的系统误差。
②半径为200 m的大圆航迹坐标解算结果迭代发散,解算结果为平面中误差超过80 cm,高程中误差大于5 m,无法满足海底控制点精密标校要求。
③田字航迹平面中误差为5 cm,平面解算精度低于小圆,分析其原因是,圆形的对称性优于田字,小圆平面精度优于田字;但田字航迹在高程方向增加了约束,高程中误差为6 cm,优于小圆高程精度。
④利用3种单一航迹,组成4种组合航迹,组合后的航迹解算结果并非都优于单独航迹,其中,小圆加田字解算平面中误差为5 cm,高程中误差为9 cm,精度低于小圆、田字航迹结果。
2)方案②:使用IGG方法进行抗差处理,选用平均声速1498.39 m/s进行海底控制点坐标解算。由于实验区域位于海洋环境比较复杂的浅海区,观测值中必定会存在较大的偶然误差乃至粗差。经典最小二乘法对粗差十分敏感,且没有抗差的能力,使用经典最小二乘法解算的结果必定会受观测数据中的粗差影响。为了减小粗差对数据解算精度的影响,将IGG选权迭代法应用于水下声学定位解算,其解算结果如表2所示。

表2 IGG法海底控制点解算结果 单位:m
从表1和表2可以看出,观测数据中的粗差对最小二乘法解算精度影响严重,在使用了IGG抗差估计法后,解算精度显著提高,各航迹的坐标精度明显优于经典最小二乘法。其中:
①7种航迹中,平面精度最高的仍为小圆航迹;高程()方向上,田字航迹的中误差最小,解算精度相对最优。
②大圆航迹在最小二乘解算时发散(如表1所示,平面中误差超过80 cm),无法获得高精度的海底控制点坐标位置;而采用IGG抗差估计法时,大圆平面解算精度大幅提高,解算精度和小圆解算精度基本相近,北方向()和东方向()中误差分别由原来的85、82提高到了3、3 cm。
③同时与大圆组合的航迹解算精度均明显提升,套圆组合后,方向、方向定位精度分别从58、58提高到4、4 cm;大圆加田字组合后,方向、方向定位精度分别从58、52提高到3、3 cm;套圆加田字组合后,方向、方向定位精度分别从44、41提高到4、3 cm。
3)方案③:使用一次范数最小方法进行抗差处理,选用平均声速1498.39 m/s进行海底控制点坐标解算。前人研究表明[27],在观测数据中存在粗差较多的情况下,IGG选权迭代法并不一定能达到预期的精度。为了更好地进行观测数据的抗差处理,采用一次范数最小法对海底应答器坐标位置进行解算,其解算结果如表3所示。

表3 一次范数最小法海底控制点解算结果 单位:m
对比表2和表3可以看出:
1)采用IGG选权迭代法的方案②和采用一次范数最小估计的方案③,其小圆航迹海底控制点解算精度相当,平面位置解算精度都在2 cm左右,高程位置解算精度在5 cm左右。
2)大圆航迹的解算结果表明,利用一次范数最小法解算的坐标精度优于IGG选权迭代法解算的坐标精度1 cm左右。分析原因是:大圆航迹半径大,受浅海环境影响,观测数据中粗差较小圆航迹和田字形航迹多,而IGG选权迭代法首次平差是在等权的条件下进行的,这使得粗差被分配到各个改正数上,影响下1次水声测量观测值权的确定;而一次范数最小法首次平差时的权由残差决定,因此一次范数最小法能更好地减小可能存在的粗差影响,从而提高整体抗差性。
3)与大圆组合的航迹解算精度均有明显提升,在方案③中的7种不同航迹的解算结果较方案①和方案②总体精度有较大提高。
对比以上3种方案解算结果可知:当观测数据中存在粗差时,最小二乘法受粗差影响最大,平面和高程解算精度都不高,不能满足高精度海底控制点标校要求;当观测数据含有较多粗差时,一次范数最小法要优于IGG法,它具有较强的粗差探测能力,在第1次平差时能快速确定粗差位置,并对相应观测值进行降权,能较好地处理初次平差时的权分配问题;利用一次范数最小法能快速获取高精度海底控制点坐标位置。
4 结束语
本文介绍了海底大地控制点标校基本原理与方法,通过将抗差估计算法应用于水下声学定位解算,对比了IGG选权迭代和一次范数最小2种抗差估计方法在水下声学定位中的精度。实验结果表明,一次范数最小法抗差能力较强。最后利用浅海海底大地控制点实测数据验证后得到以下结论:
1)不同标校航迹情况下海底控制点坐标解算精度不同。实验证明小圆航迹具有良好图形对称性,平面解算精度最高;田字航迹具有交叉点约束,高程解算精度最高。
2)经典最小二乘法在水下声学定位计算中受粗差和系统误差影响较大,解算精度不高,结果也不稳定,不能满足海底控制点精密标校需要。利用IGG和一次范数最小法2种抗差估计法解算海底控制点坐标,可将海底控制点定位精度由分米级提高到厘米级。
3)实验结果表明,1次范数最小法抗差能力较强,尤其是在标校航迹图形结构不好的情况下,通过一次范数最小法解算得到的海底控制点坐标精度更高、更稳定,有效提高了海底控制点标校作业的灵活性。
[1] SPIESS F N. Suboceanic geodetic measurements[J]. IEEE Transaction Geoscience Remote Sensing, 1985, GE-23(4): 502-510.
[2] SPIESS F N. Analysis of a possible sea floor strain measurement system[J]. Marine Geodesy, 1985, 9(4): 385-398.
[3] SPIESS F N, CHADWELL C D, HILDEBRAND J A, et al. Precise GPS/acoustic positioning of seafloor reference points for tectonic studies[J]. Physics of the Earth & Planetary Interiors, 1998, 108(2): 101-112.
[4] OBANA K, KATAO H, ANDO M. Seafloor positioning system with GPS-acoustic link for crustal dynamics observation-a preliminary result from experiments in the sea[J]. Earth Planets and Space, 2000, 52(6): 415-423.
[5] MOCHIZUKI M, SATO M, YOSHIDA Z, et al. Seafloor geodetic observations around Japan[C]//The Institute of Electrical and Electronic Engineers(IEEE).Proceedings of the 2002 Interntional Symposium on Underwater Technology. Tokyo Japan: IEEE, 2002: 239-243.
[6] GAGNON K, CHADWELL C D, NORABUENA E. Measuring the onset of locking in the Peru-Chile trench with GPS and acoustic measurements[J]. Nature, 2005, 434(7030): 205-208.
[7] SWEENEY A D, CHADWELL D C, HILDEBRAND J A, et al. Centimeter-level positioning of seafloor acoustic transponders from a deeply-towed interrogator[J]. Marine Geodesy, 2005, 28(1): 39-70.
[8] XU P, ANDO M, TADOKORO K. Precise, three-dimensional seafloor geodetic deformation measurements using difference techniques[J]. Earth, Planets and Space, 2005, 57(9): 795-808.
[9] FAVALI P, BERANZOLI L. Seafloor observatory science: a review[J]. Annals of Geophysics, 2006, 49(2/3): 515-567.
[10] FUJITA M, ISHIKAWA T, MOCHIZUKI M, et al. GPS/acoustic seafloor geodetic observation: method of data analysis and its application[J]. Earth, Planets and Space, 2006, 58(3): 265-275.
[11] MATSUMOTO Y, ISHIKAWA T, FUJITA M, et al. Weak interplate coupling beneath the subduction zone of Fukushima, NE Japan, infered from GPS/acoustic seafloor geodetic observation[J]. Earth, Planets and Space, 2008, 60(6): 9-12.
[12] IKUTA R, TADOKORO K, ANDO M, et al. A new GPS-acoustic method for measuring ocean floor crustal deformation: application to the Nankai Trough[J]. Journal of Geophysical Research, 2008, 113(B2): B02401.
[13] LOVELESS J, MEADE B. Geodetic imaging of plate motions, slip rates, and partitioning of deformation in Japan[J]. Journal of Geophysical Research, 2010, 115(B2): B02410.
[14] YOKOTA Y, ISHIKAWA T, SATO M, et al. Heterogeneous interplate coupling along the Nankai Trough, Japan, detected by GPS-acoustic seafloor geodetic observation[J]. Progress in Earth and Planetary Science, 2015, 2(1): 10.
[15] CHEN H Y, RYOYA I, LIN C H, et al. Back-arc opening in the western end of the Okinawa trough revealed from GNSS/acoustic measurements[J]. Geophysical Research Letters, 2018, 45(1): 137-145.
[16] 杨元喜, 徐天河, 薛树强.我国海洋大地测量基准与海洋导航技术研究进展与展望[J].测绘学报, 2017, 42(1): 5-12.
[17] 李林阳, 吕志平, 邝英才.高精度海底大地控制网建立方法分析与比较[J].测绘科学技术学报, 2018, 35(4): 343-348.
[18] 邝英才, 吕志平, 蔡汶江, 等. GNSS/声学系统定位精度影响因素分析[J].测绘通报, 2018(12): 15-20.
[19] 赵建虎, 梁文彪. 海底控制网测量和解算中的几个关键问题[J].测绘学报, 2019, 48(9): 1197-1202.
[20] CHEN Guanxu, LIU Yang, LIU Yanxiong, et al. Adjustment of transceiver lever arm offset and sound speed bias for GNSS-acoustic[J]. Remote Sense, 2019, 11(13): 1606.
[21] 周江文. 经典误差理论与抗差估计[J]. 测绘学报, 1989, 18(2): 115-120.
[22] 杨元喜. 抗差估计理论及其应用[M]. 北京: 八一出版社, 1993: 303.
[23] XU P. Sign-constrained robust least squares, subjective breakdown point and the effect of weights of observations on robustness[J]. Journal of Geodesy, 2005, 79(1-3): 146-159.
[24] 王潜心, 徐天河, 许国昌. 粗差检测与抗差估计相结合的方法在动态相对定位中的应用[J].武汉大学学报(信息科学版), 2011, 36(4): 476-480.
[25] 林国标, 刘立龙, 蔡成辉, 等. 一种基于丹麦法的改进型双步M估计[J].大地测量与地球动力学, 2015, 35(2): 235-238.
[26] 赵新秀, 王解先. 一次范数最小估计的两种算法[J].测绘工程, 2010, 19(2): 13-15.
[27] 赵言, 黎慕韩, 王鹏, 等. 一次范数最小和选权迭代联合的抗差法[J].大地测量与地球动力学, 2016, 36(4): 331-333.
[28] 王振杰, 李圣雪, 聂志喜, 等. 水声定位中一种大入射角声线跟踪方法[J].武汉大学学报(信息科学版), 2016, 41(10): 1404-1408.
Precision calibration method of subsea geodetic control points based on norm minimum estimation
HU Zhiyuan1,2, WANG Panlong3, TANG Qiuhua1,2, ZHOU Xinghua1,2, ZHOU Dongxu2
(1. School of Surveying and Mapping Science and Engineering, Shandong Science and Technology University, Qingdao, Shandong 266590, China; 2. The First Institute of Oceanography, Ministry of Natural Resources of the People's Republic of China, Qingdao, Shandong 266061, China; 3. Geodetic Data Processing Center, Ministry of Natural Resources of the People's Republic of China, Xi’an 710054, China )
Aiming at the problem that it is liable to gross errors and system errors for least squares adjustment method commonly used in underwater acoustic positioning of marine surveying and mapping, leading to low solution accuracy and weak stability, the paper proposed a solving method of underwater control points: the basic principle and method of subsea geodetic control point calibration were introduced, and the GNSS/underwater acoustic positioning model was given; then IGG weighted iterative method and L1-norm minimum method were selected to implement the precise calibration of underwater acoustic positioning data. Experimental result showed that the L1-norm minimum method could effectively resist the disturbance of abnormal observation with a strong anti-error ability, and achieve the centimeter level positioning accuracy of subsea control points in shallow sea.
seafloor geodetic control point; underwater acoustic positioning; L1-norm minimum method; weighted iterative method
P228
A
2095-4999(2020)03-0015-08
胡致远,王盼龙,唐秋华,等. 范数最小估计的海底大地控制点精密标校方法[J]. 导航定位学报, 2020, 8(3): 15-22.(HU Zhiyuan,WANG Panlong, TANG Qiuhua, et al. Precision calibration method of subsea geodetic control points based on norm minimum estimation[J].Journal of Navigation and Positioning, 2020, 8(3): 15-22.)
10.16547/j.cnki.10-1096.20200303.
2019-12-13
国家重点研发计划(2016YFB0501703);国家自然科学基金(41904040)。
胡致远(1996—),男,山东青岛人,硕士研究生,研究方向为水声定位数据处理算法研究。
