基于空谱联合异常度的高光谱异常目标检测

张 炎，华文深，黄富瑜，王强辉，索文凯

陆军工程大学石家庄校区电子与光学工程系，河北 石家庄 050003

引 言

高光谱遥感(hyperspectral remote sensing)兴起于20世纪80年代，是一种融合光谱学理论与成像原理的前沿技术[1]。高光谱图像的光谱分辨率达到了纳米级别，具有大量波段，是一种“图谱合一”的三维图像。光谱特征能够表达地物的本质特性，在目标检测领域运用光谱特征进行检测更加可靠。由于光谱信息库的不完善和大气校正的困难，不需要先验知识的异常目标检测应用更加广泛，成为了近年来的研究热点[2]。

最经典的异常目标检测算法是Reed等[3]在1990年提出的RX算法(reed-xiaoli detection，RXD)，最开始应用于多光谱图像，后来成为高光谱异常目标检测的基准算法，其本质是基于广义似然比检测的一种恒虚警率异常目标检测算法，通过计算背景的协方差矩阵和均值向量获得被检测像元与背景像元的马氏距离，从而得到检测结果。但由于异常目标在高光谱图像中尺寸较小，出现概率低，全局RX算法(global RX，GRX)的检测精度较低，虚警率较高。为提高检测效果，Taitano等[4]提出了一种局部RX算法(local RX，LRX),采用滑动双窗口模型进行检测，有效提高了检测精度。但由于RX算法及其改进算法[5]本质上属于线性检测算法，没有挖掘出高光谱数据的非线性特性，检测效果仍然不够理想。Kwon等[6]通过引入核函数提出了KRX算法(kernel RX，KRX)，该算法是一种典型的非线性检测算法，将线性不可分的原始数据投影到高维特征空间，增强了目标和背景的差异性，提高了检测精度，降低了虚警率。但由于KRX算法及其改进算法[7-8]存在计算复杂度高等问题，因此，为突破传统的广义似然比检测和非线性核函数等方法的局限性，提高检测精度，需要对算法进行进一步的改进和优化。

当前大多数高光谱异常目标检测算法只关注目标和背景在光谱信息方面的差异，忽略了两者空间信息的差异，事实上，高光谱图像异常不仅包括光谱异常，同时也包括空间异常。如果能够挖掘出图像的空间信息，对高光谱数据的光谱信息和空间信息进行综合分析，可以有效地提高检测算法的精度[9]。因此，提出了一种基于空谱联合异常度的高光谱异常目标检测算法(space-spectrum joint anomaly degree for hyperspectral anomaly target detection,SSJHAD)，该算法不需要假设背景模型，基于滑动双窗口的基础上对图像进行检测。光谱角距离是一种常用的计算像元之间光谱信息差异的有效方法，但由于光谱角距离不能充分挖掘出像元之间的非线性差异，因此引入核函数将核光谱角作为度量像元之间光谱差异的方法，计算出中心像元的光谱异常度(spectral anomaly degree，SADspec)；通过构建空间窗模型得到图像块灰度向量的手段来描述空间方面的差异性，得到中心像元的空间异常度(spatial anomaly degree，SADspat)；最后将两者进行加和得到最终的空谱联合异常度(space-spectrum joint anomaly degree，SSAD)，从而来判定像元是否属于异常目标。

1 基于空谱联合异常度的高光谱异常目标检测算法

基于空谱联合异常度的高光谱异常目标检测算法建立在滑动双窗口的基础上，中心像元为待测像元，内外窗之间的像元为背景像元，如图1所示。分别求解中心像元和背景像元之间的光谱差异和空间差异得到光谱异常度和空间异常度，并将两者进行加和得到空谱联合异常度，从而得到检测结果。

图1 算法的滑动双窗口检测模型Fig.1 The sliding double window model of algorithm

1.1 光谱异常度

光谱异常度的原理是利用像元之间光谱信息的差异，逐个求解中心像元与背景像元的核光谱角，同时设定阈值ε1，若距离大于阈值，则中心像元的光谱异常度加1，反之，则加0，利用滑动窗模型即可得到所有像元的光谱异常度。

1.1.1 核光谱角

光谱角(spectral angle，SA)是一种能够衡量两个光谱向量差异程度的方法[10]。两个光谱向量之间的光谱角越小，说明两者的光谱曲线越相似，属于同一种物质的概率越高；反之，属于同一种物质的概率越低。假定原始数据集为X=[x1,x2，…,xN]∈RD×N，其中D为光谱维数，N为像元数，其列向量为像元的光谱向量，则光谱角的表达式为

(1)

从式(1)可以看出光谱角只和向量的方向有关，和向量本身的长度无关，因此，光谱角能够有效地度量两个光谱曲线的差异性，同时具有很好的抵抗乘性干扰的能力，不受光谱强度变化的影响[11]。但由于光谱角不能很好地挖掘出高光谱图像的非线性特性，检测精度不高，因此引入核函数求解像元之间的核光谱角(kernel spectral angle，KSA)能够有效地挖掘图像的非线性特性，提高检测精度[12]。通过非线性映射函数φ可将原始数据集X映射到高维特征空间得到：φ(X)=[φ(x1),φ(x2)，…,φ(xN)]∈RQ×N，Q远远大于D，则光谱角在高维特征空间中的表达式为

(2)

由于非线性映射函数φ一般不可知，无法直接在高维特征空间中进行计算，从而转化为核函数在原始特征空间点积计算的形式，一般采用高斯径向基(Gaussian radial Basis function，GRBF)核函数，表达式为

(3)

利用核函数性质k(x,y)=〈φ(x),φ(y)〉将高维特征空间的数据运算映射为低维空间的核函数运算，则可得到核光谱角的表达式

(4)

通过逐个求解中心像元和背景像元的核光谱角，根据得到的核光谱角结果的平均值设置阈值ε1，通过比较得到高光谱图像中像元的光谱异常度SADspec。

1.2 空间异常度

高光谱图像中的像元成千上万且都不是独立存在，以像元为中心的邻域能够表达该像元的空间结构信息[13]。为了能够定量的衡量不同像元空间信息的差异程度，基于双窗口的基础上以坐标点为(i,j)的待测像元为中心建立一定大小的空间窗，得到图像块灰度向量H(i,j)，内外窗均表示直径为奇数大小的正方形，内窗直径定义为rin，外窗直径定义为rout，如图2所示。通过求解中心像元和背景像元图像块灰度向量的欧式距离衡量空间信息方面的差异。由于图像中存在很多噪声点，并且都是独立存在的，容易与异常目标相混淆，建立空间窗能够有效地避免噪声点的影响。

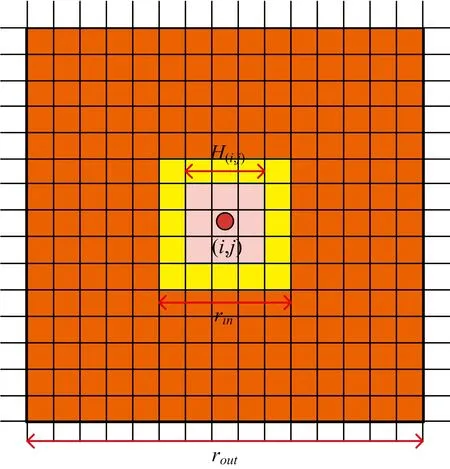
图2 空间异常度的检测模型Fig.2 Detection model of spatial anomaly degree

高光谱图像具有大量波段，为降低计算的复杂度，本文先利用典型的PCA(principal component analysis)算法对原始高光谱图像进行降维，将得到的前M个主成分作为空间异常度检测的输入图像。在降维之前首先根据虚拟维度(virtual dimensionality,VD)确定原始数据的本征维数(intrinsic dimensionality,ID)，从而确定M的值。文献[13]中表明L2距离能够作为度量图像块之间空间结构相似性的一个可靠准则。因此，通过计算中心像元和背景像元的图像块灰度向量的欧式距离，并根据得到的欧式距离结果的平均值设定阈值ε2，若距离大于阈值，则中心像元的空间异常度加1，反之，则加0，对得到的M个图像的空间异常度进行加权和得到最终空间异常度。像元的空间异常度SADspat定义为

SADspat(i,j)=q1SAspat(i1,j1)+

q2SAspat(i2,j2)+…+qMSAspat(iN,jN)

(5)

(6)

虚拟维度：降维的本质是将高维特征空间的原始数据投影到低维特征空间中，低维特征空间的维数称为本征维数。通过求取虚拟维数确定本征维数，选择相应的波段数目。基于Neyman-Pearson探测理论分析的HFC(Harsanyi-Farrand-Chang)是确定VD值的常用方法，原理如下：

(7)

(8)

其中，μ是未知量。当图像像元N足够大时，方差约为

(9)

检测率Pd和虚警率Pf的定义表达式为

(10)

1.3 空谱联合异常度

中心像元的空谱联合异常度由光谱异常度和空间异常度共同决定，定义为

SSAD(i,j)=SADspec(i,j)+SADspat(i,j)

(11)

像元的空谱联合异常度越大，表明该像元属于异常目标的概率越大。

按照上述方法遍历高光谱图像中的所有像元，得到每个像元的空谱联合异常度，并设置阈值，异常度高于阈值的像元为异常像元，反之，为背景像元，从而获得图像的最终检测结果。

2 结果与讨论

为充分验证本文算法的可靠性和有效性，采用了三组真实的高光谱数据进行实验仿真。仿真环境为：CPU处理器为Intel Core i7-3635QM，主频为2.40 GHZ，安装内存为8 GB，软件为Matlab2018a。

2.1 数据

数据1选取的是AVIRIS传感器拍摄的美国San Diege海军机场的部分数据，波长范围为0.37～2.51 μm，去除低信噪比和水蒸气吸收比较严重的波段，保留波段为189个；空间分辨率为3.5 m，截取的区域大小为100×100像素，存在38个异常目标；数据2和数据3选取的是AVIRIS传感器拍摄的美国洛杉矶机场的数据，波长范围为0.37～2.51 μm，去除低信噪比的波段和水蒸气吸收比较严重的波段，保留波段为205个；其空间分辨率为7.1 m，截取的区域大小为100×100像素，分别存在2个异常目标和17个异常目标。图3为数据1的伪彩色图像和目标分布图；图4为数据2的伪彩色图像和目标分布图；图5为数据3的伪彩色图像和目标分布图。

2.2 参数选择

本文算法是基于双窗口模型的基础上进行检测，利用双窗口进行选择待测像元和背景像元。因此内外窗口的尺寸大小对检测结果具有很大的影响，如果选择的内外窗口使背景像元中存在异常目标则会很大程度上影响检测的精度。对本文中采用的三组数据进行具体分析，可以发现，不同数据的异常目标的大小和分布不同，选取的理想窗口尺寸也存在差异。数据1的异常目标大小基本为4×4像素的范围内，相邻目标的距离大约为11个像素，因此，选取的内外窗的尺寸分别为rin=9，rout=11时能够获得最为纯净的背景像元，避免了异常目标的污染，具有最好的检测效果；同理，数据2选取的内外窗尺寸大小为rin=11，rout=17时能够获得最好的检测效果；由于数据3中的不同异常目标的大小和距离存在很大的变化，因此，通过大量实验结果得出最为理想的尺寸大小为rin=9，rout=15。

图3 伪彩色图像(a)及其相应的目标分布(b)Fig.3 Pseudo-color image (a) and its corresponding target distribution (b)

图4 伪彩色图像(A)及其相应的目标分布(b)Fig.4 Pseudo-color image (a) and its corresponding target distribution (b)

图5 伪彩色图像(a)及其相应的目标分布(b)Fig.5 Pseudo-color image (a) and its corresponding target distribution (b)

2.3 检测结果与分析

为充分说明SSJHAD算法的可靠性和适用性，分别利用RX算法、LRX算法、KRX算法、只计算光谱异常度的SHAD算法、将光谱角替代SSJHAD算法中核光谱角的SSJAD算法与SSJHAD算法对三组数据分别进行仿真实验，图6为六种算法对实验数据1的异常目标检测效果图，图7为六种算法对实验数据2的异常目标检测效果图，图8为六种算法对实验数据3的异常目标检测效果图，可以看出SSJHAD算法的检测效果相比其他五种算法有了明显地提高，虚警率较低。

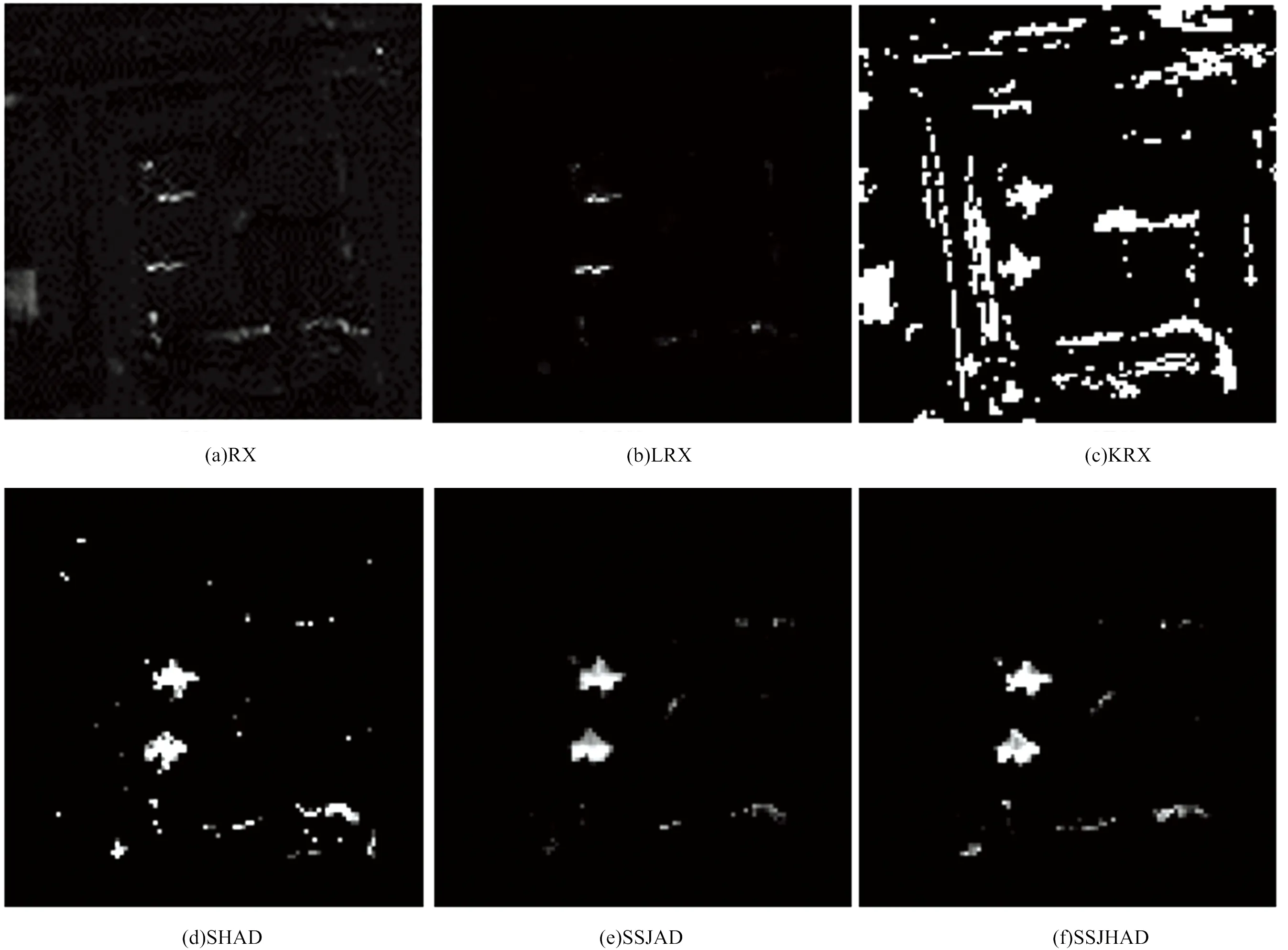
图7 六种算法在数据2上的检测结果对比Fig.7 Comparison of anomaly detection results of six algorithms on data 2

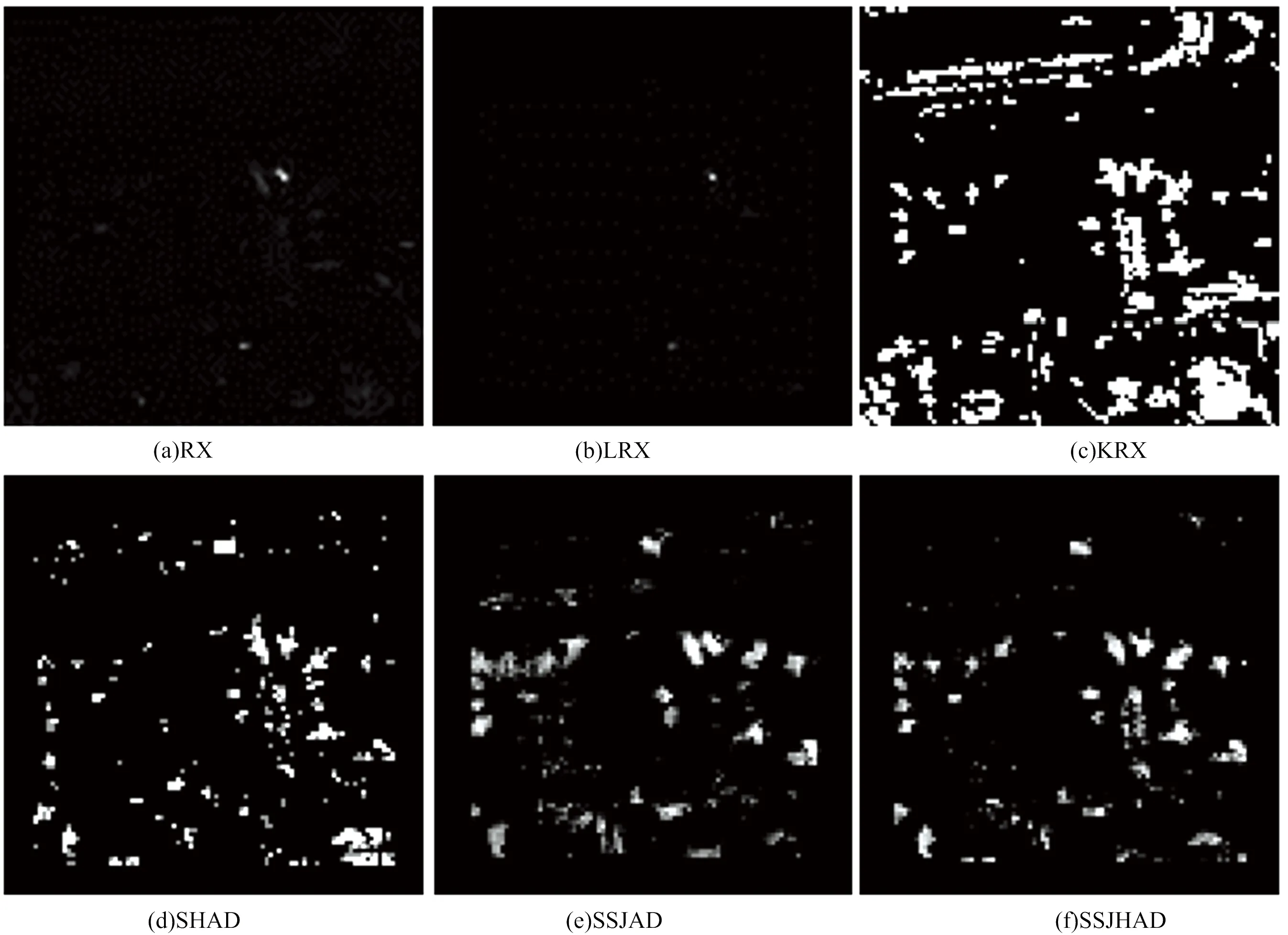
图8 六种算法在数据3上的检测结果对比Fig.8 Comparison of anomaly detection results of six algorithms on data 3

通过观察三组异常目标检测效果图，可以看出，RX算法和LRX算法基本上无法识别三组高光谱数据的异常目标；KRX算法虽然能够检测出绝大多数的异常目标，但虚警率很高，检测结果中残留了许多背景目标；SHAD算法的检测效果虽然优于前两个算法，但仍然没有检测出所有的异常目标，虚警率依然很高；SSJAD算法能够检测出所有的异常目标，残留的背景目标也有所减少；SSJHAD算法在检测所有异常目标的同时，能够有效地抑制背景信息，异常目标检测效果图明显优于其他五种算法。

为了能够定量的比较六种算法的检测效能，利用ROC(receiver operating characteristic curve)曲线和AUC(area under the curve)值进行说明比对。若ROC曲线越向左上方弯曲，AUC值越大，检测效能越好；反之，检测效能越差。六种算法检测三组数据的ROC曲线如图9所示，不同算法检测结果的AUC值和运行时间如表1所示。

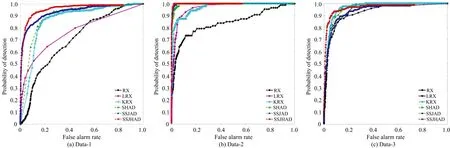
图9 六种算法的ROC曲线对比Fig.9 Comparison of ROC curves of six algorithms

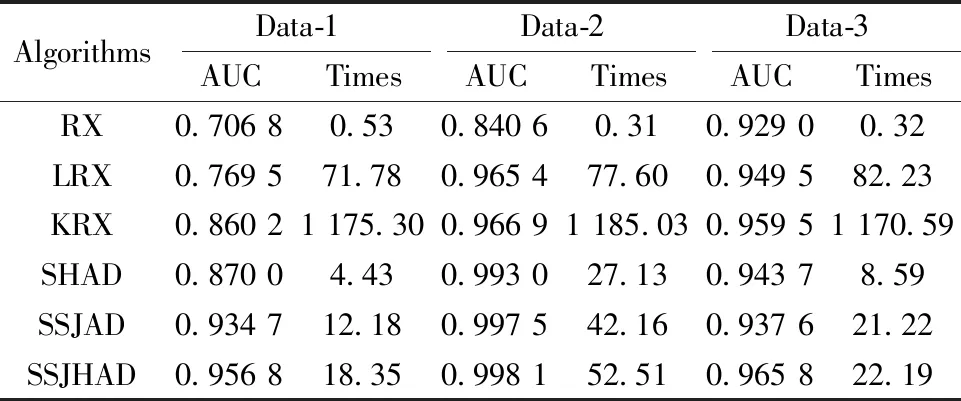
表1 三组数据的AUC值和运行时间(s)Table 1 AUC values/execution times with the three sets of data(s)

从ROC曲线图和AUC值可以看出，SSJHAD算法在三组不同数据的检测效能都远远高于其他五种算法，具有一定的可靠性和适用性；同时，在虚警率较低的前提下，仍然具有很高的检测精度，说明SSJHAD算法能够有效地抑制背景信息的干扰。而RX，LRX和KRX算法在数据1的检测效果相比数据2和数据3有明显的差距，原因在于这三种算法更适用于背景单一的数据，对于背景复杂的高光谱数据，检测效果会明显下降；将KRX算法和RX算法或者SSJHAD算法与SSJAD算法的检测结果进行对比，可以看出，通过引入核函数能够有效地挖掘出数据的非线性特性，提高算法的检测精度。对比SHAD算法和SSJHAD算法的检测效能，说明了异常目标和背景不仅仅在光谱信息上存在差异，在空间信息上也存在差异，有效地将图像的空间信息与光谱信息相结合进行检测能够一定程度地提高检测精度。综上所述，SSJHAD算法同时考虑了异常目标的光谱异常和空间异常，并引入了核函数对常用的光谱角进行改进得到核光谱角来衡量像元之间的光谱差异。因此，SSJHAD算法应用于异常目标检测能够取得很好效果。

从表1中可以看出，在保证检测精度前提下，KRX算法的运行速度远低于RX算法、LRX算法、SHAD算法、SSJAD算法和SSJHAD算法，表明其计算复杂度较高。

3 结 论

针对目标与背景的异常不仅仅体现在光谱异常，同时还存在空间异常的特点，本文提出了一种基于空谱联合异常度的高光谱异常目标检测算法。算法基于滑动双窗口的基础上，提出了光谱异常度和空间异常度的概念，并将两者进行加和得到联合异常度对图像进行检测。算法不需要假设背景模型，对不同的高光谱图像都具有很好的检测效果，具有普适性。在光谱异常度方面，引入了核函数来挖掘出高光谱图像的非线性特性，用核光谱角计算出像元的光谱异常度，增强了背景和目标的可分性。在空间异常度方面，通过计算不同像元的图像块向量的欧式距离能够有效地降低噪声对检测精度的影响。实验表明，本文所提的SSJHAD算法运行速度要优于KRX算法，相比于其他算法，提高了检测精度，降低了虚警率。