基于GM(1,1)模型的陕西省旅游人数预测
2020-06-12王南丰沈李欢
王南丰,沈李欢
(西安财经大学 统计学院,陕西 西安 710000)
0 引言
旅游业作为综合性产业之一,其健康可持续的发展能够推动地区经济的快速增长。随着经济的发展和国家节假日的调整,近年来我国旅游人数逐年上涨。旅游人数作为现代旅游业良好发展的重要衡量指标之一,若能对其进行科学合理地预测,就能够把握地区旅游业未来发展的基本趋势,从而预先制定相应的战略和对策,以确保旅游业的可持续发展。
陕西省位于中国西北地区,独特的地理环境和深厚的历史文化积淀使其成为中国旅游资源最丰富的省份之一。近年来,陕西省旅游业发展进入新的阶段,全省旅游业呈现出良好发展态势。特别是在2018年,陕西省全年接待境内外游客总计6.30亿人,比上年增长20.5%,旅游总收入达到5994.66亿元,增长了24.5%。由此可以看出,蓬勃发展的陕西旅游业,已经成为地区经济发展的重要引擎。
鉴于以上分析,本论述基于2011年~2018年度陕西省旅游人数数据,通过GM(1,1)模型对陕西省未来5年的旅游人数进行科学预测,以期为陕西省旅游业的发展规划提供一定的参考依据。预测结果显示,陕西省未来5年的旅游人数分别为73015.9330万人次、85716.9814万人次、100627.4933万人次、118131.8427万人次和138681.275万人次。通过比对预测数据和旅游人数原始数据发现,陕西省未来5年的旅游人数将呈现出逐年增长的趋势。同时还发现,预测值与原始数据十分接近,进而说明使用GM(1,1)模型对陕西省旅游人数进行预测具有很高的可靠性。
1 理论与方法介绍
1.1 理论介绍
灰色系统理论是由邓聚龙(2005)提出的。它是一种基于少量数据的新兴研究方法,其主要作用是对人们日常生活、工作等方面本征性灰色系统做数据建模、数据分析、数据预测、决策分析及最后对其进行控制的过程。其主要内容是包括以灰色方程、灰色矩阵以及灰色代数系统为基础生成的理论体系,以灰色序列为基础生成的方法体系,以灰色关联空间为依托关系生成的分析体系,以灰色模型为核心而生成的综合理论体系。
灰色系统预测具体内容指在研究与分析系统因子之间协调作用与互相影响的基础上,建立系统主行为特征量和关联因子的灰色动态模型群,进而通过求解模型对其进行预测。灰色系统预测主要分为区间预测、灾变预测、系统预测、波形预测、数列预测等。当前使用最广泛的灰色预测模型之一就是数列预测即一阶微分GM(1,1)模型。GM(1,1)模型是指基于随机原始序列,经其按照时间进行累加后而形成新的时间序列所展现的规律,其规律可使用一阶线性微分方程的解来逼近。
1.2 GM(1,1)模型的建立过程
第一步,确定原始数据。
设时间序列 X(0)中有n个观察值,则将原始序列可记为:X(0)={X(0)(1),X(0)(2),...,X(0)(n)}
第二步,级别比检验。
原始数据确定后,需要对原始数据进行级别比的计算,判断原始数据的级别比是否均落入可容覆盖范围内,级别比的计算公式为λ(k)=X(0)(k-1)/X(0)(k)(k=2,3,...,n),其中k为时刻,只有当计算所得级别比均在可容覆盖范围内,就能对该数据使用灰色预测方法,进而对其建立GM(1,1)模型进行分析。否则,应先对原始数据进行变换处理,使其变换后数据的级别比处于可容覆盖范围内,再对其进行GM(1,1)模型的建立。
第三步,建立GM(1,1)模型。
(1)计算累加生成列
由于所选取数据具有随机性,不能对数据直接进行处理,所以对数列进行X(0)-AGO(累加),使之构成数列X(1)={X(1)(1),X(1)(2),...,X(1)(n)}。因此累加生成列为:
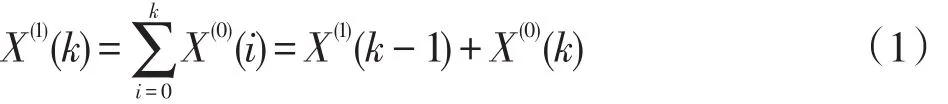
(2)参数估计
令Z(1)为X(1)紧邻均值生成序列:

根据公式(1)和公式(2)可写出GM(1,1)模型的灰微分方程是X(0)(k+1)+az(1)(k)=μ式中,a是发展系数,μ被叫做内生控制灰数。设aˆ为待估参数向量,αˆ=(a,μ)',求解可知 αˆ如公式(3):

其中B和Yn表示如公式(4):
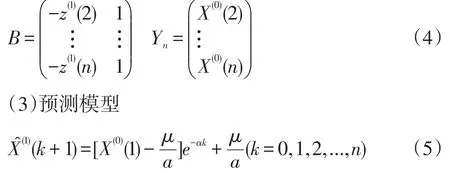
(4)计算预测值
根据公式(5)的预测模型可初步计算出预测值。因为预测模型是在累加序列的基础上完成的,因而要对得到的预测值进行累减还原,才可得到最终的预测值。其公式为:X(1)(k)=X(0)(k)-X(0)(k-1)。根据预测模型以及累减还原得到最终的预测值后应对其进行检验,判断该预测值残差检验、关联度检验、后验差检验是否都通过,如三者检验全都通过,则可以用所建模型对其进行预测;否则,应进行残差修正,残差修正完成后再建立GM(1,1)模型对其进行预测,因而GM(1,1)模型的最后一步是对其进行检验。
(5)模型检验
①残差检验
累减生成序列是将原始序列的前后两个数据进行相减。根据预测模型的公式计算Xˆ(1)(i),并对Xˆ(1)(i)进行累减得到 Xˆ(0)(i),计算原始数据序列 X(0)(i)和 Xˆ(0)(i)的绝对误差序列以及相对误差序列。观察残差检验结果,当计算的相对误差值全部小于0.5%,则可说明该模型精度较高。
其中,绝对误差序列为:

②关联度检验
首先计算出Xˆ(0)(i)和X(0)(i)之间的关联系数,再计算两者关联度。据经验,当 ρ=0.5时,关联度值大于0.6即可表明通过检验。当计算出在Xˆ(0)(k)和X(0)(k)两者之间关联系数后,再计算关联系数的均值,即该均值r叫做 Xˆ(0)(k)序列和 X(0)(k)之间的关联度。η(k)叫做预测序列和原始序列两者的关联系数。设预测序列和原始序列分别如下:

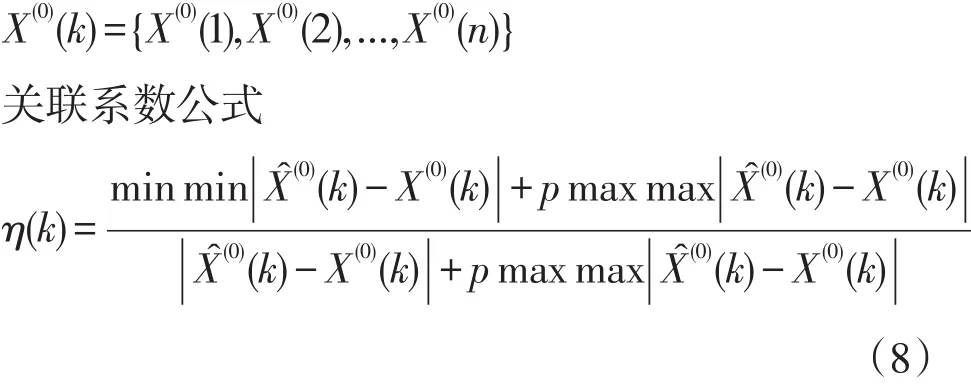
公式(8)中 | Xˆ(0)(k)-X(0)(k)| 称为第 k 个点 X(0)与 Xˆ(0)绝之间的绝对误差。其中,minmin| Xˆ(0)(k)-X(0)(k)| 是两级最小差,maxmax| Xˆ(0)(k)-X(0)(k)|是两级最大差。 ρ叫做分辨率,0<ρ<1,常取 ρ=0.5。通常情况下,由于数据单位的不一致将会导致结果存在误差,为了消除数据间误差,因而在计算关联系数之前应先对数据进行标准化处理,本论述使用初值法对数据进行处理,即用每一序列所有数据依次除以该序列的第一个数据。
③后验差检验
后验差检验步骤,首先分别计算原始序列的标准差S1与绝对误差序列的标准差S2,进而计算出二者比值为C=S2S1。后验差检验的两个重要指标分别是C和P。C值越小则说明S1比S2大,S1大说明原始数据离散程度大,S2小说明残差离散程度小。指标C值越小越好,C值小就说明尽管原始数据很离散,但模型计算所得预测值与实际值之差的离散程度并不大。
P为小误差概率。P越大则说明模型的拟合值或预测值分布也相对均匀。综合评定预测模型的精度可根据指标C和P。模型的精度由C和P共同描述。通常把模型的精度分为以下四级,具体见表1所列。

表1 模型精度的具体数值
2 基于GM(1,1)模型的陕西省旅游人数的预测及分析
2.1 原始数据的选取及级比检验
本论述选取陕西省2011年~2018年旅游人数数据作为原始数据,在原始数据基础上建立GM(1,1)模型进行预测分析,所用数据均来源于《陕西省统计年鉴》和陕西省统计公报。使用GM(1,1)模型预测之前,首先应对数据进行级别比检验,若计算的级别比在可容覆盖范围内,则可对其构建GM(1,1)模型进行预测分析。通过计算得知可容覆盖范围为Θ=(0.7788,1.2840)。 通 过 级 别 比 公 式 λ(k)=X(0)(k-1)/X(0)(k)计算陕西省2011年~2018年每年旅游人数的级别比λx(k),计算结果见表2所列。观察表2发现级别比全部落入可容覆盖范围内,可对旅游人数直接建立GM(1,1)模型。
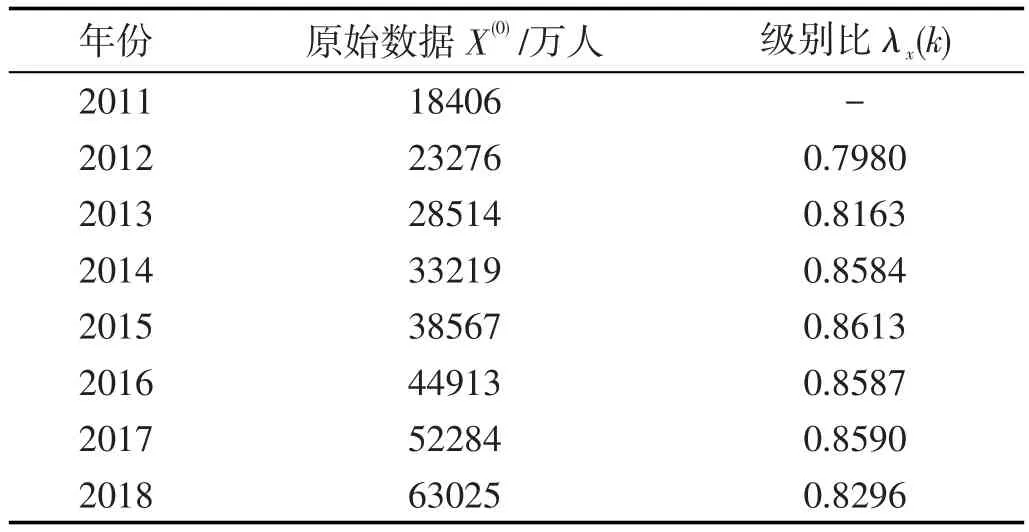
表2 2011年~2018年原始数据及级比检验
2.2 构建GM(1,1)模型
通过对表2级别比检验结果分析后发现,可以直接对其进行GM(1,1)模型构建。利用公式(1)和公式(2)可分别计算出累加序列X(1)(k)和紧邻均值生成序列Z(1),计算所得结果见表3所列。

表3 累加序列及紧邻均值生成序列
通过观察表3的结果并结合公式(4),可写出矩阵B和Yn,见下所列。

通过对矩阵B和Yn进行计算并结合公式(3),得出参数向量αˆ如下。

通过公式(5)以及公式(8)可得出预测模型如公式(10)。根据公式(10)可计算出预测值见表4所列。得出预测值之后,对模型进行残差检验、关联度检验和后验差检验,并判断模型是否均通过残差、关联度以及后验差检验。
首先根据公式(6)和公式(7)计算出原始数据和预测值之间的绝对误差和相对误差,结果见表4所列。进而对其进行残差检验。根据表4可看出,相对误差中有部分值大于0.5%,并结合残差检验的理论,说明该模型未通过残差检验。

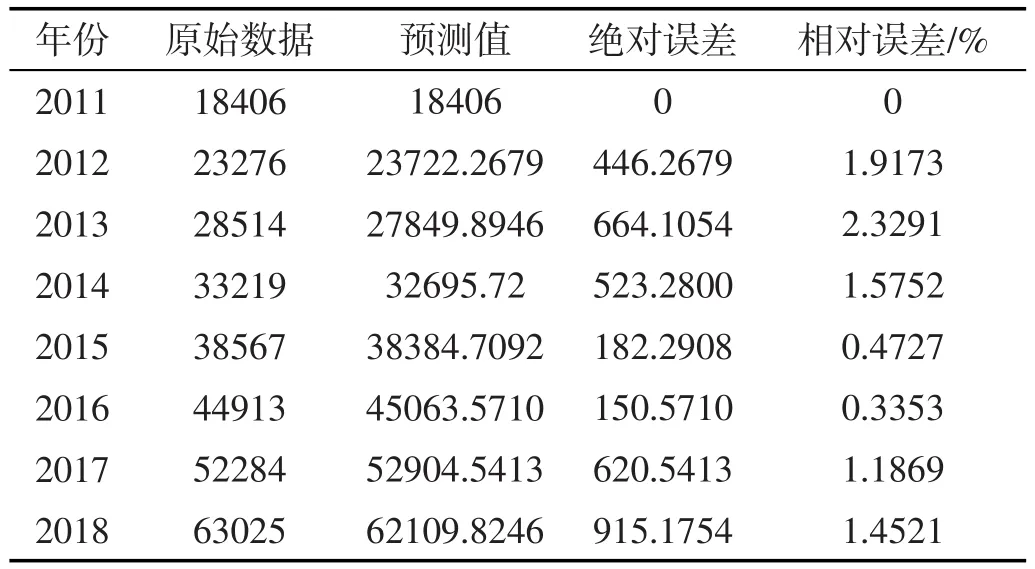
表4 2011年~2018年预测值、绝对误差和相对误差
对模型进行残差检验之后,再对模型进行关联度检验,通过公式(8)计算得出关联系数见表5所列。由表5得出,关联度等于0.5758,不满足当 ρ=0.5时,r>0.6的规则,因而该模型未通过关联度检验。
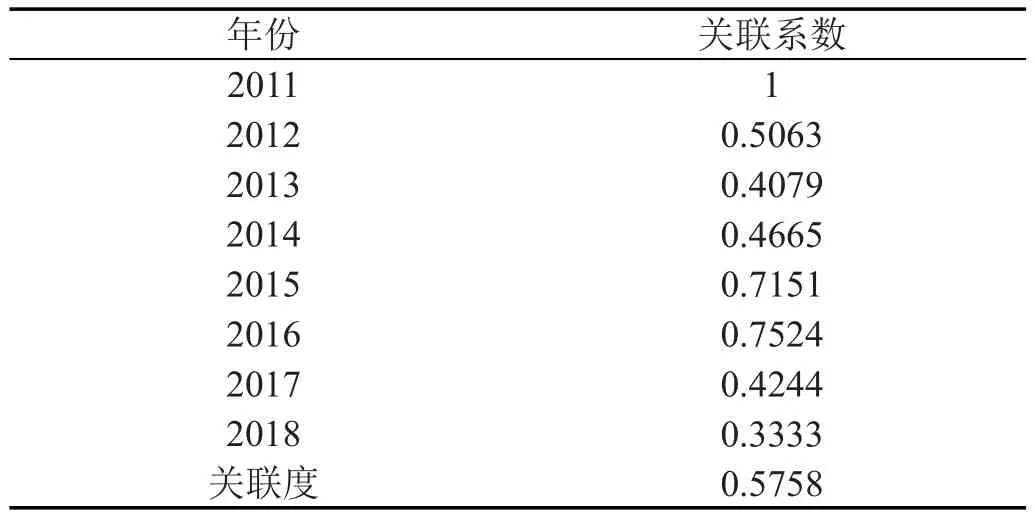
表5 2011年~2018年关联系数及关联度
关联度检验完成后,再对其进行后验差检验。后验差检验具体指标是用C值和P值进行检验。C值具体计算方法是利用Excel软件分别计算已知残差的标准差和原始数据的标准差,分别为Se2=287.0820和14104.7612,计算一致后验差比值=0.0204。C值计算完成后,进而计算P值,P值具体计算是先计算S0和ek,公式S0=0.6745S1,ek= ||Δk-,当所得 ek都小于 S0时,P 值等于1。计算得S0=0.6745S1=9513.6614
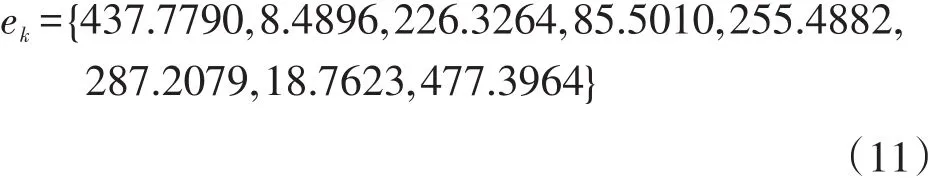
综上,C=0.0204<0.35。观察公式(11)得知,所有的ek均小于S0,所以P=1>0.95。综合C和P并检验结果,判断该模型较好,通过后验差检验。
综上,通过残差检验、关联度检验以及后验差检验的分析结果,得知该模型未通过残差检验和关联度检验,所以需要对模型进行修正。采用残差对该模型进行修正,再对修正后的数据建立GM(1,1)模型对其进行预测。首先利用公式(1)和公式(6)计算出残差序列及残差累加序列见表6所列。

表6 残差序列及残差累加序列
其次根据公式(4)及表6计算结果计算矩阵B和Yn,得出矩阵 B和Yn。

再计算出参数向量αˆ如下:
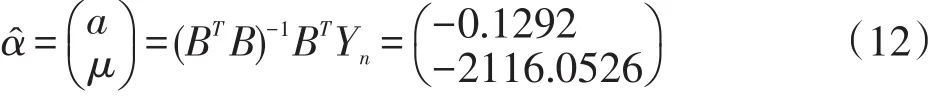
最后根据公式(5)及公式(12)可得出经过残差修正后的模型。
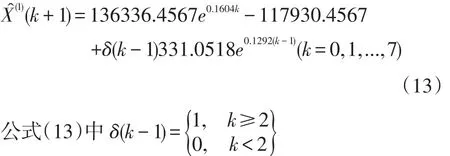
根据公式(6)和公式(7)得出修正后残差计算结果见表7所列。

表7 修正后的残差计算表
根据表7可知,修正后的模型精度相对于表4而言具有显著的提高,因而可以利用经过残差修正后的模型来对陕西省旅游人数进行预测。通过公式(13)计算得到的陕西省2011年~2023年度旅游人数预测值见表8所列,将表8中所显示的陕西省2011年~2023年度旅游人数预测值与2011年~2018年度旅游人数的原始值进行比对,并描绘出陕西省旅游人数的原始值和预测值之间的关系,如图1所示。
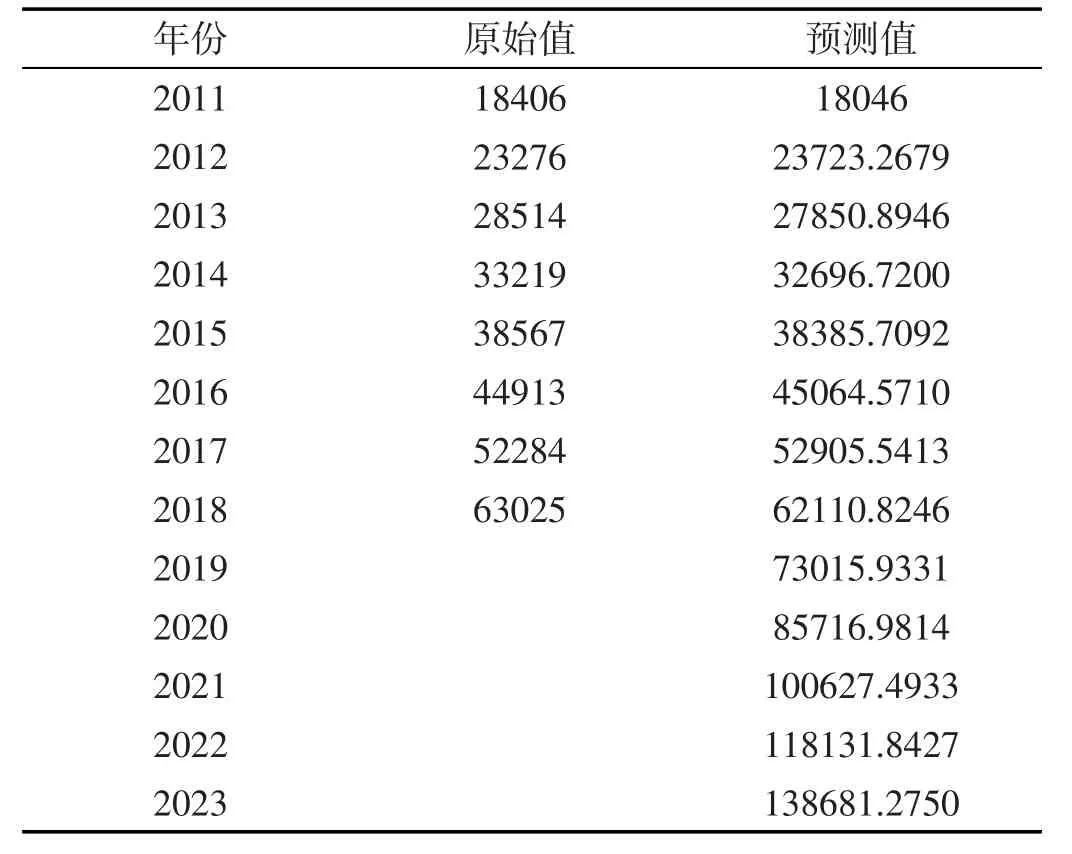
表8 陕西省2011年~2018年旅游人数的原始值及2011年~2023的预测值(单位:万人)

图1 旅游人数原始数据及预测数据
通过表8和图1可以得出,陕西省未来五年(2019年~2023年)的旅游人数分别为73015.9331万人、85716.9814万人、100627.4933万人、118131.8427万人、138681.2750万人,并且还发现陕西省未来五年旅游人数将呈现逐年增长的态势。通过预测值和对陕西省2011年~2018年的原始值进行比对,发现预测值基本接近原始值,这也进一步说明了通过GM(1,1)模型预测陕西省未来五年旅游人数具有很高的可靠性。
3 结论分析与对策建议
3.1 结论分析
本论述基于灰色系统理论,构建GM(1,1)模型对陕西省未来五年的旅游人数进行预测,预测结果显示,陕西省未来5年的旅游人数分别为73015.9330万人次、85716.9814万人次、100627.4933万人次、118131.8427万人次和138681.275万人次。同时还发现,通过GM(1,1)模型预测的陕西省未来5年旅游人数呈现逐年递增的态势。此外,通过将GM(1,1)模型的估计值与陕西省2011年~2018年度旅游人数实际值进行比对发现,预测值和实际值较为接近,这说明本论述所构建的预测模型是可靠的,进而表明使用GM(1,1)模型对陕西省未来5年旅游人数进行预测具有一定的科学性。
3.2 对策建议
对旅游人数进行预测有利于对旅游业发展进行科学规划,同时也有利于提高游客满意度。基于研究结论并结合陕西省的旅游发展概况,本论述提出如下对策建议。
(1)以多元化视角构建陕西省旅游形象,制定科学合理的总体规划。在未来五年旅游人数逐年增长的良好环境下,陕西省应以多元化视角构建旅游形象,制定科学合理的总体规划。各景区应坚持可持续发展观,以游客为本,以市场为导向,依靠科技进步,改变传统旅游资源粗放式开发利用的状况,科学制定旅游总体规划,推动旅游资源的创新利用,实现旅游产业转型升级。同时注重多元化和特色化,形成良好的生态旅游环境,凸显生态旅游效应,促进陕西省社会经济协调发展。
(2)加快陕西省旅游基础设施建设,完善旅游产业管理体制。基础建设是促进旅游业发展根本要素,加强陕西省旅游通道建设及区域内部旅游的运输体系建设,优化旅游景点周边的设施布局,为游客提供方便舒适的旅游环境。同时加强旅游业与相关产业融合发展,完善旅游产业管理体制,加强旅游人才队伍建设,提高旅游服务质量。
(3)拓宽陕西省各个景区的旅游宣传途径,增强景点的服务能力。首先鼓励景区创建自己的微信公众号或微博公众号等,经常发一些与该景点有关的内容,以吸引游客;其次加大对旅游从业人员的培训力度,提高服务意识和质量;最后运用新技术,提供低收费景点自助讲解服务,降低单位游客旅游消费成本,提高游客的满意度。
