改进的遗传k-means算法及其应用
2020-06-12邱建林
黄 松,邱建林
(南通大学 信息科学技术学院,江苏 南通 226019)
0 引 言
k-means聚类算法[1-3]是一种基于划分的数据挖掘技术,此算法操作简单、效率高、局部搜索性能好,且能有效处理大规模数据,但由于聚类数目的不确定性和初始聚类中心选取的随机性,使得聚类结果波动大、准确率低。针对这些问题,文献[4]通过改进聚类有效性函数来选取最佳聚类数;文献[5]利用粒计算的属性分辨能力,降低了属性值过大对聚类有效性函数的影响,从而得到最佳聚类数;文献[6]提出了一种优化初始聚类中心的方法,使聚类结果更准确;文献[7]提出了一种基于改进遗传算法的k-means聚类方法,将遗传算法的思想引入到聚类算法中,使得聚类结果更稳定,聚类效果更好。但都只考虑了聚类数目或者初始聚类中心,文献[8]提出了一种双重遗传k-means算法(DGKA),该算法利用双层遗传算法确定聚类数目和自适应控制初始聚类中心,在算法结束时能同时获得较优聚类数和初始聚类中心,但此算法的内层算法过于依赖外层算法,使得聚类结果不稳定。因此,针对此问题,本文提出了一种改进的遗传k-means聚类算法(PGKMA),该算法采用并行计算的方式,解决了DGKA算法中聚类稳定性过于依赖外层算法的问题,通过两个经典实例验证了算法的准确性和有效性,并利用该算法对玉米样本集进行聚类分析,对聚类后的玉米良种集,采用DTOPSIS(dynamic technique for order preference by similarity to ideal solution)法[5]综合评价并排序,获得精英玉米品种,从而指导玉米良种选育工作。
1 相关知识
1.1 k-means算法
k-means算法的核心思想是根据随机给定的聚类数k,从数据集中随机选择k个对象作为初始聚类中心,通过某种度量方式(一般采用欧式距离)将数据对象划分到与之距离最近的簇中,然后重新计算聚类中心,再次划分,不断重复此过程,直到聚类中心不再发生改变。
定义1 设X=(x1,x2,…,xn),Y=(y1,y2,…,yn),X与Y的欧式距离定义为
(1)
k-means算法描述如下:
算法1:k-means聚类算法
输入:包含n个对象的数据集D,聚类数k
输出:聚类结果S
(1) begin
(2) 从D中随机选取k个对象作为初始聚类中心{c1,c2,…,ck};
(3) fori=1:n
(4) forj=1:k
(5) 计算Di与cj的欧式距离,并将其赋给距离最近的簇;
(6) endfor
(7) endfor
(8) 计算每个类的平均值并更新聚类中心;
(9) 重复(3)到(8),直到聚类中心不再发生改变;
(10) 输出最终聚类结果S;
(11) end
1.2 遗传算法
遗传算法(genetic algorithm,GA)是一种借鉴生物界进化规律,按照适者生存,优胜略汰的遗传机制,逐步演化形成的一种全局搜索方法。其主要特点是对目标函数没有连续可微的限制;遗传操作不直接作用于数据空间;具有隐含的并行性和全局搜索能力;在搜索空间中能够自适应调整进化方向,获取问题的近似最优解。因此,遗传算法被人们广泛地应用于聚类分析[9]、图像识别[10]、组合优化[11]和机器学习[12]等领域。
1.3 DTOPSIS综合评价法
DTOPSIS是一种逼近理想解的综合排序方法[13],通过为需要进行评价的样本建立评价矩阵,对评价矩阵进行无量纲化处理后加权获得决策矩阵,然后计算品种的正负理想解,并计算各品种与正负理想解之间的距离,进而得到各品种与理想解之间的相对接近度,最后对相对接近度进行排序获得最优的品种。其具体步骤为:
(1)建立样本指标评价矩阵
(2)
(2)对评价矩阵无量纲化处理
(3)
(3)建立规范化决策矩阵R,其中Rij=Wj*Zij,Wj为第j个指标权重;
(4)计算品种的正负理想解
(4)
(5)计算各品种与正负理想解之间的距离
(5)
(6)计算各品种对理想解的相对接近度
(6)
(7)将相对接近度按大小进行排序,最大的即为最优个体。
2 改进的遗传k-means聚类算法的设计
针对k-means算法初始聚类中心过于依赖聚类数目的问题,采用并行计算的方式获取聚类数目和初始聚类中心,并行计算过程如图1所示。

图1 并行计算结构
PGKMA算法解决了DGKA算法内层算法过于依赖外层算法的问题,不仅能同时获取当前最佳聚类数和初始聚类中心,而且聚类结果更稳定、更准确。综合考虑算法的特殊性,设计了合适的编解码策略,适应度函数和遗传操作。
2.1 编码与解码策略


图2 初始聚类中心染色体编码
PGKMA解码策略,染色体每d个等位基因串组成一个聚类中心。
2.2 适应度函数设计
定义2 簇内对象相似度可由平均类内距表示为
(7)
其中,xij为第i类的第j个对象;Ni为第i类样本容量;ci为第i类聚类中心。
定义3 簇间对象差异性可由类间距表示为
(8)
聚类结果的优劣直接决定着适应度函数值的高低,而平均类内距和类间距直接反映了聚类结果的好坏,因此,适应度函数定义为
(9)
平均类内距越小,类间距越大,聚类效果越好,适应度函数值越大。
2.3 遗传操作设计
2.3.1 选择操作
PGKMA算法采用锦标赛选择法,设N,n分别为父代,子代种群个数,当n≤0.8×N时,从父代种群中随机选取m个个体,计算适应度函数值,保留适应度函数值最大的个体到子代;当n>0.8×N时,随机选取m个个体,计算适应度函数值,保留适应度函数值最小的个体到子代;从而增加了种群多样性,防止算法收敛于局部最优解;同时将精英个体直接复制到下一代中,保证了进化进程的正确性。
2.3.2 交叉操作设计
采用单中心交叉方式,即依概率Pc随机产生一个交叉点(该交叉点位于每条染色体聚类中心的交界处),交换两条染色体交叉点后长度为d的部分,从而获得两条新的染色体。单中心交叉如图3所示。
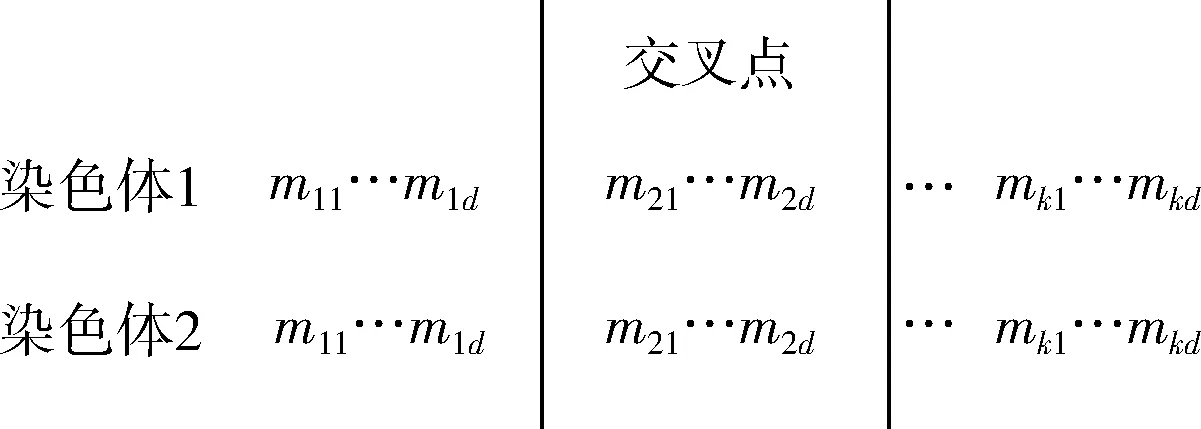
图3 单中心交叉
2.3.3 变异操作设计
采用单中心k-means变异操作,即依概率Pm在聚类中心交界处随机产生一个变异点,变异长度为d,将与之距离最近的数据点赋给该变异中心,并重新计算均值替换变异中心编码值。
2.4 实验结果与分析
本文选取UCI标准数据库中的Iris和Glass数据集作为实验数据,分别从最佳聚类数K、最佳初始聚类中心C、类内距ICS、类间距ICD、适应度函数值F、迭代次数G和正确率,对传统k-means算法、双重遗传k-means算法(DGKA)和本文PGKMA进行比较。在Windows 10操作系统下,硬件条件为Intel(R)Core(TM)i7-8550u CPU @ 1.80 GHz 1.99 GHz,8 GB内存,使用Matlab编程实现。
PGKMA算法步骤如下:
input:数据集,算法参数
output:最佳聚类数Kopt,最佳初始聚类中心Copt,聚类结果
步骤1 根据聚类数K的取值范围,为各K值初始化对应的聚类中心种群;
步骤2 同时对各聚类中心种群进行k-means聚类操作,得到聚类结果;
步骤3 计算各K值下的适应度函数值,并记录适应度函数最大值;
步骤4 比较各K值下的适应值,并记录最大值F1max及其对应的聚类数K;
步骤5 若time1=5或gen1=100,转步骤9,否则,转步骤6;
步骤6 若Kopt=K,则time1=time1+1,Fmax=F1max,转步骤8;否则转步骤7;
步骤7Kopt=K,time1=1,Fmax=0,转步骤8;
步骤8 通过遗传操作更新各K值下的聚类中心种群,gen1=gen1+1,转步骤2;
步骤9 获取Kopt对应的聚类中心种群;
步骤10 k-means聚类得到聚类结果;
步骤11 计算适应值,并记录最大值F2max,聚类中心Copt;
步骤12 若time2=10或gen2=150,则输出结果,算法结束,否则转步骤13;
步骤13 若F2max=Fmax,则time2=time2+1,转步骤15,否则,转步骤14;
步骤14Fmax=F2max,time2=1,转步骤15;
步骤15 遗传操作获得新一代聚类中心种群,gen2=gen2+1,转步骤10。
PGKMA算法采用混合结束策略,即当Fmax连续10代保持不变,或者算法达到最大迭代次数时,输出最佳聚类数,最佳初始聚类中心,聚类结果。
Iris是一个150*4的数据集,包含150个对象,每个对象包含4个属性,最佳聚类数为3;Glass是一个214*9的数据集,包含214个对象,每个对象包含9个属性,最优聚类数为6。实验参数设置见表1。

表1 实验参数设置
表2和表3是两类数据集在3个算法下的最佳聚类数K、最佳初始聚类中心C和迭代次数G的测试结果。从表中可以看出,传统KM算法迭代次数最多,DGKM算法和PGKMA算法均有一定程度减少,且PGKMA算法迭代次数最少。
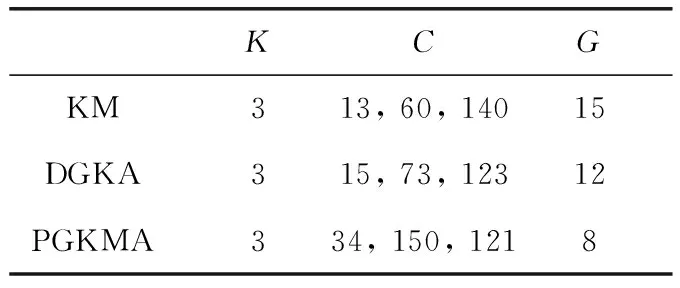
表2 Iris数据集测试结果

表3 Glass数据集测试结果
为了进一步比较算法的正确性和聚类结果的稳定性,将每种算法运行30次,实验结果见表4,表5。

表4 Iris数据集运行结果

表5 Glass数据集运行结果
通过表4、表5和图4、图5可以看出,传统KM算法的类内距离最大,类间距离最小,DGKM和PGKMA算法均有所改善,且PGKMA算法的类内距离最小,类间距离最大。从适应度函数值来看,适应度函数值的大小与类间距离成正比,类内距离成反比,且PGKMA算法的适应度函数值最大。针对传统KM算法在求解聚类时类间个体差异不明显和DGKM算法聚类结果不稳定的问题,PGKMA算法加强了类内个体的紧凑度和不同类间个体的差异度,提高了聚类结果的稳定性。

图4 Iris数据集聚类结果分析
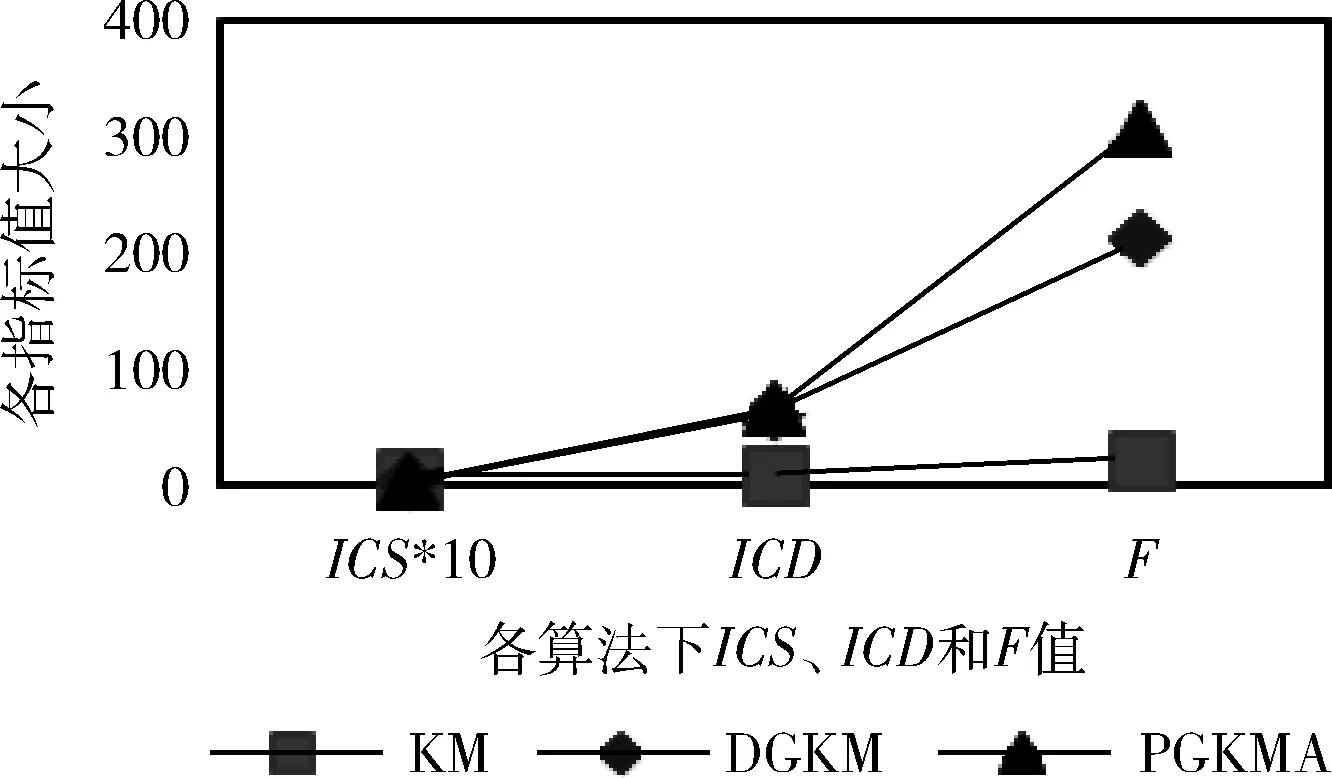
图5 Glass数据集聚类结果分析
从图6可知,传统KM算法聚类结果受聚类数和初始聚类中心的影响最大,正确率最低。DGKM算法通过双重算法对聚类数进行控制,改善了聚类结果的质量,提高了聚类的准确率,但聚类质量过于依赖聚类数目的确定。PGKMA算法解决了DGKM算法存在的问题,并进一步提高了聚类结果的准确率。
3 改进的遗传k-means聚类算法的应用
本文选取南通市农业信息组2006年玉米数据集(Y组)作为样本集,见表6,该样本集包括51个子类对象和15个父类对象,每个对象包含全生育期、株高、穗粗、行粒数、千粒重、出籽率、小区产量等20多种属性。
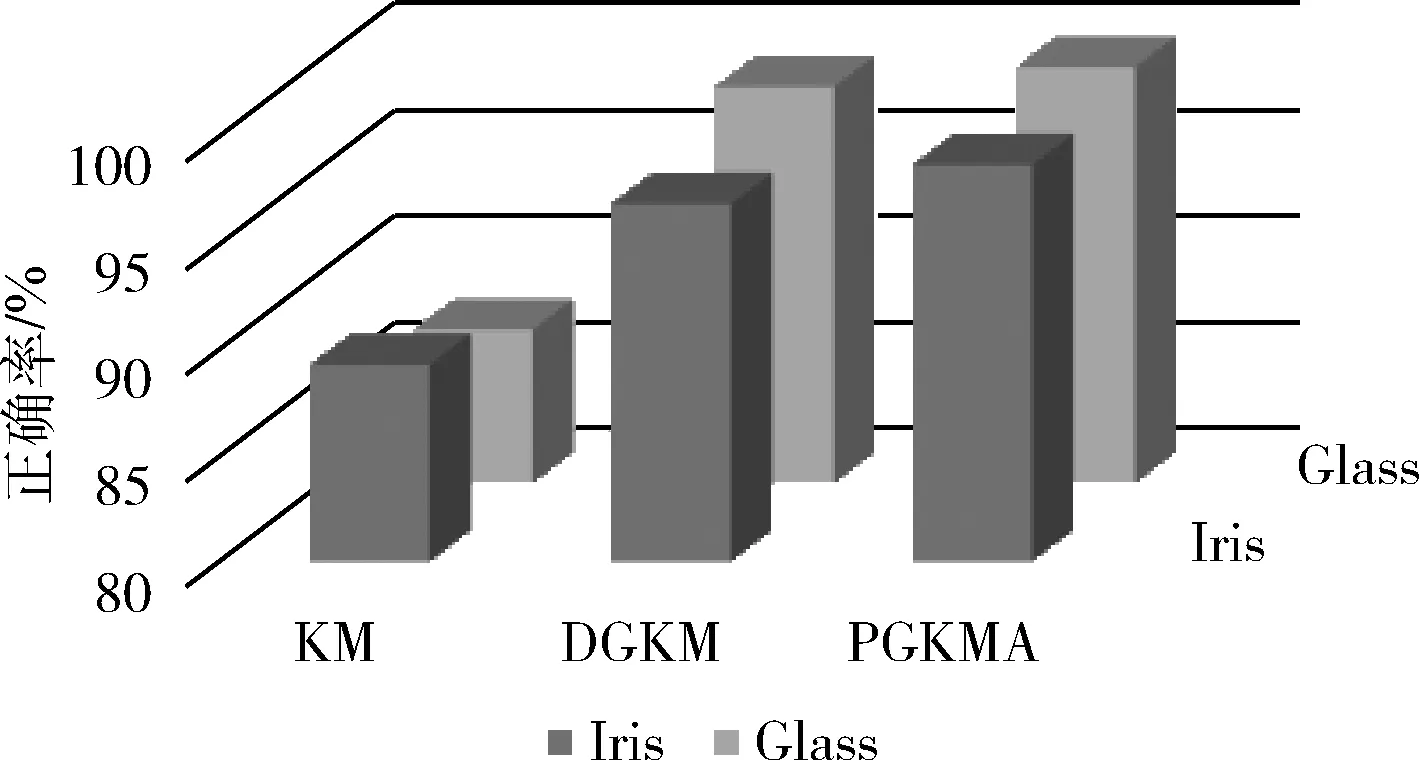
图6 Glass和Iris数据集聚类正确率对比
3.1 玉米样本集的最佳聚类数和初始聚类中心选取
采用并行遗传k-means聚类算法进行离散化,然后运用基于遗传算法的粗糙集属性约简算法对玉米数据子类进行横向约简,得到最小约简集为{全生育期,穗高,穗粗,行粒数,千粒重,出籽率,小区产量},约简后的数据表见表7。
由表8和图7可知,本文算法得到的聚类结果平均类内距最小,类间距最大,有效性函数值最大,聚类结果最好。最佳聚类数为3,最佳初始聚类中心是5,31,37,聚类结果如下:
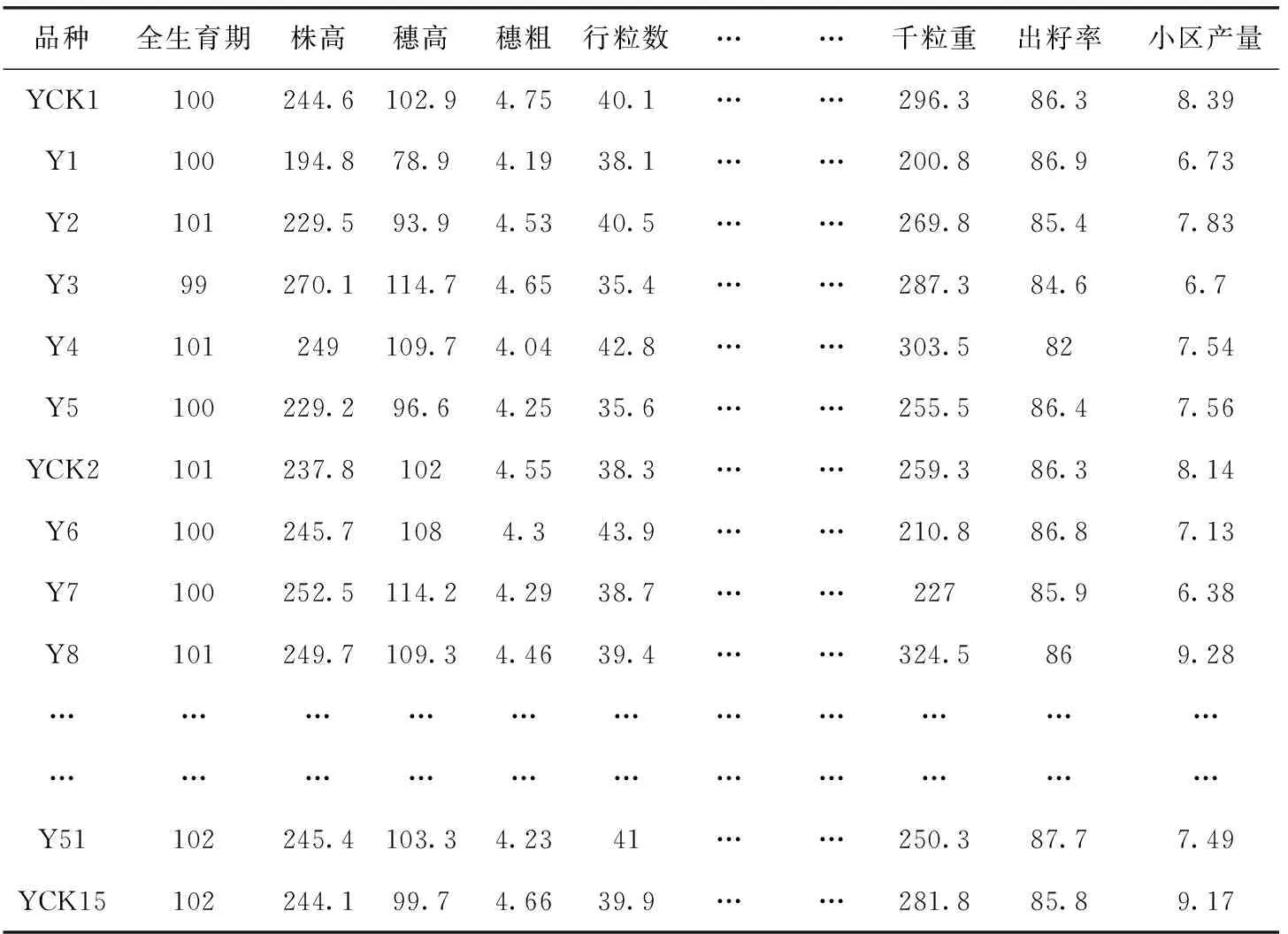
表6 玉米数据集
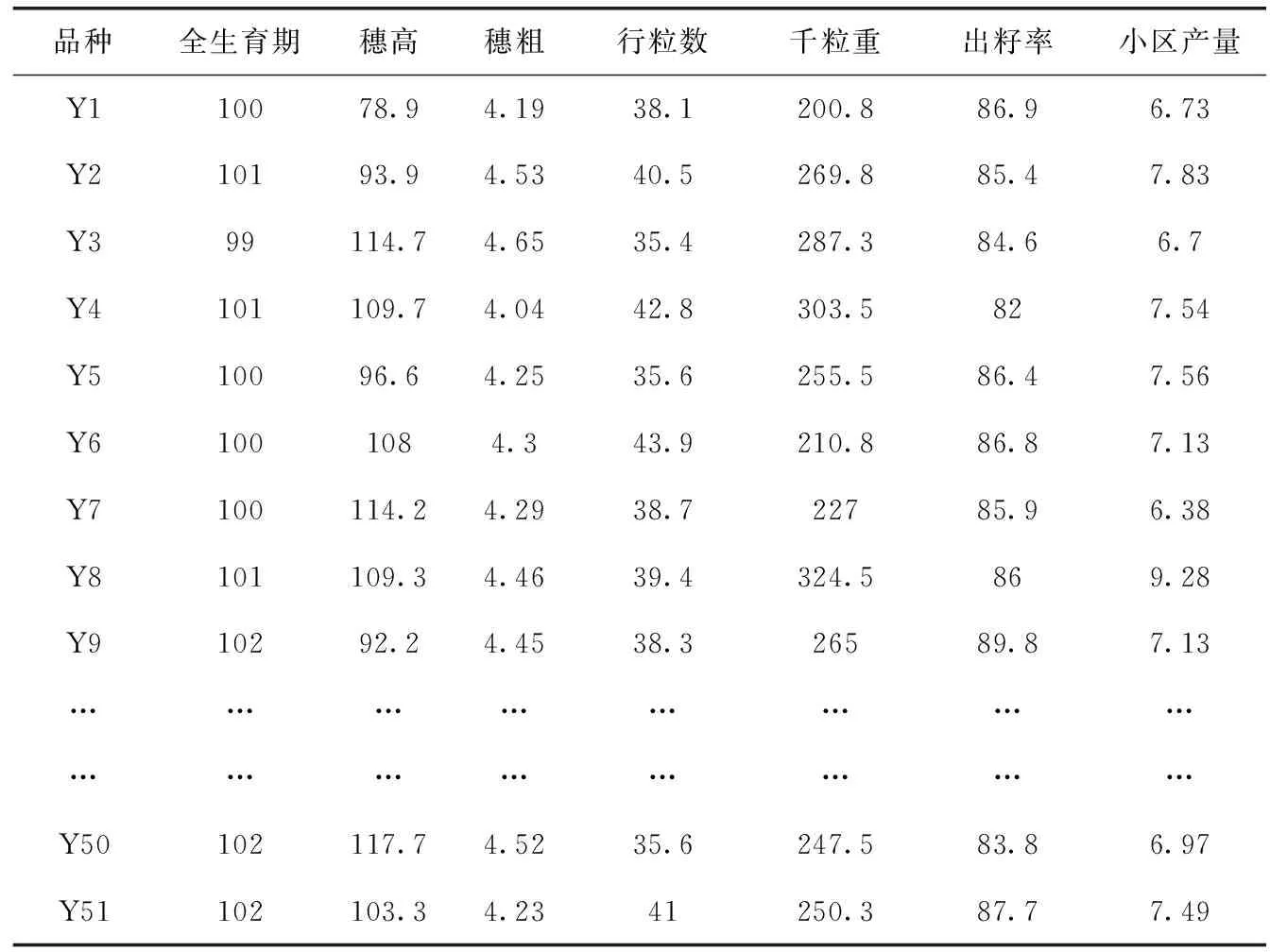
表7 属性约简后的玉米样本集
第一类:Y1,Y3,Y30,Y50,Y51;
第二类:Y2,Y6,Y7,Y8,Y10,Y14,Y16,Y20,Y22,Y23,Y24,Y26,Y27,Y28,Y29,Y31,Y32,Y34,Y35,Y36,Y37,Y39,Y44,Y46,Y47,Y48,Y49;
第三类:Y4,Y5,Y9,Y11,Y12,Y13,Y15,Y17,Y18,Y19,Y21,Y25,Y33,Y38,Y40,Y41,Y42,Y43,Y45。

表8 不同算法下的各项指标的数值
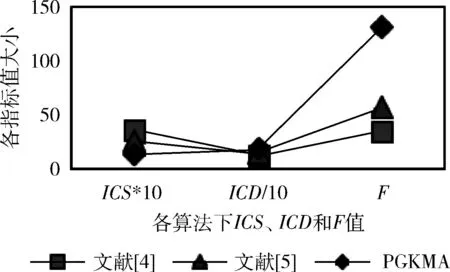
图7 聚类结果分析
表9是样本与各类各属性的平均值,从表中可以看出,第一类玉米品种的穗高、千粒重、小区产量都远低于样本平均值,所以第一类玉米属于劣种玉米类,作为异常点删除;第三类玉米品种各属性均值接近样本均值,没有明显的优势,属于普通玉米类;第二类玉米品种的行粒数、千粒重、小区产量都很高样本平均值,适用于育种。因此,本文选取第二类玉米子集作为良种集进行良种选育。
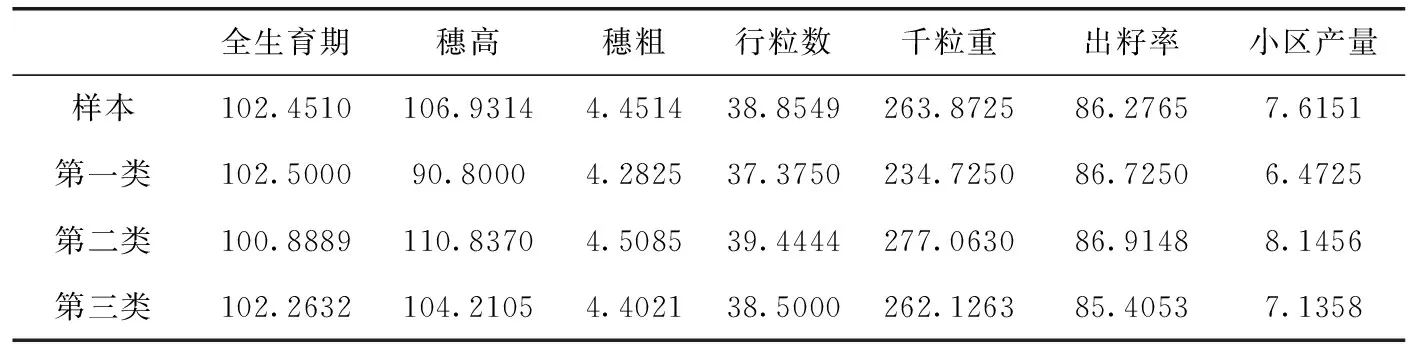
表9 样本和各类的各属性平均值
3.2 玉米种子综合评价
对聚类后的玉米良种集,采用前文介绍的综合排序方法进行排序,得到第二类良种玉米集的相对接近度为
C=
将C按大小进行排序,可得精英玉米品种为:Y47,Y49,Y48,Y29,Y20,Y22,这与南通市农业信息组所给良种排名一致。
利用PGKMA算法对玉米样本集进行聚类分析,将优良的玉米品种聚为一类,通过属性平均值分析,减少普通品种和劣种对选育工作的影响,降低了盲目育种的复杂度和工作量。采用DTOPSIS法对良种集进行综合评价,将得分较高的6个玉米品种作为精英品种,确保得到最优良的玉米品种。
4 结束语
通过两个经典实例对比分析可知,由于聚类数目的不确定性和初始聚类中心的随机性,传统的KM算法聚类结果不稳定。DGKA算法虽然在算法结束时能获得相对较优的聚类数和初始聚类中心,但聚类结果过于依赖外层聚类数的确定。本文算法采用并行计算的方式同时获得当前代最佳聚类数和初始聚类中心,设计合适的编解码方案,适应度函数以及遗传操作,提高了聚类结果的正确率和稳定性。最后,将PGKMA算法应用于玉米良种选育中,在获取精英玉米品种的同时,降低了选育工作的复杂度和工作量。
