液化气站球罐计量改进方案

王 健

（中海石油中捷石化有限公司，河北 沧州 061101）

1 球罐计量的现状

当前球罐区计量依靠石英管液位计及私服液位计读取球罐物料液位，再参照容积计算表确定球罐内液相物料的总体积和质量。

1.1 设定冬季及夏季物料的密度

见表1。

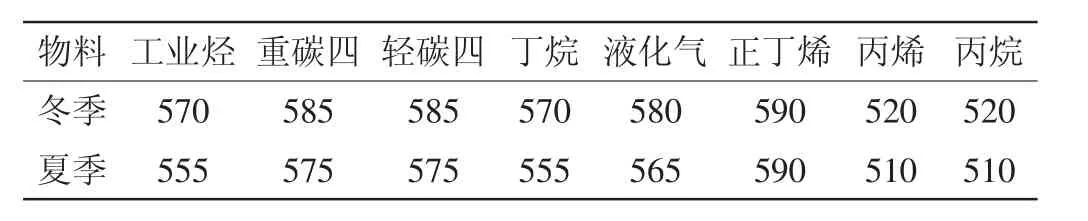
表1 冬季、夏季化工原料密度 t/m3

1.2 确定球罐内物料的质量

式中：M为物料的质量，t；ρ为物料的密度，t/m3；V为物料的体积（由容积表查得），m3。

2 误差分析

从上面的介绍的计量方法来看其测量主要存在以下几个方面的误差：

2.1 介质密度

没有对密度进行实际测量，而是使用固定的标准密度。在一定温度及压力下混合物的平均密度取决于各组分纯物质的密度以及在混合物中所占的体积分数，其值不可能是一个固定不变的数值，球罐作为一个压力容器，其压力大小、介质温度无时无刻在发生变化，甚至不同的液位高度，都会对密度造成影响。

2.2 温度影响

由于环境温度的影响，一天内日照变化、冬季夏季的温差变化，会造成储罐内介质温度的变化，特别是会形成罐内不同区域介质温度的不均衡，势必对介质的密度造成很大的影响，从而影响到对质量的计算。

2.3 压力影响

液化石油气的饱和蒸汽压，即储罐的压力，是指在一定温度下，液化石油气在密闭容器内达到气-液两相平衡状态时的蒸汽压力。液化石油气的饱和蒸汽压是随温度而变化的，温度升高，蒸汽压也增大。对于液相而言，液体不具备压缩性所以饱和蒸汽压对其密度影响不大，然而对于气相，混合气体的密度是压力、温度的函数，不同的压力、温度对应不同的密度，随着压力的增大，气相的密度也随之提高。

2.4 饱和蒸汽压的影响

没有计算饱和蒸汽的量，由于物料在压力容器中呈现出气液相平衡状态，因此在计算时，既要计算液相质量也要计算气相质量，二者之和才是物料的实际质量。

3 措施与对策

由以上误差分析，针对影响因素进行可变因素修正，以达到计量精度的要求，因此建立如下数学模型。

3.1 球罐体积计算

设液面计示数位h，液面计底部距离球罐罐底高度差为h0，液面计与竖直方向偏角为α，校正后的液面高度为h1，球罐直径为D，球罐总体积为h0，液相体积为V液，气相体积为V所，则：

3.2 物性参数与温度、压力的关系

①液相密度。

液化石油气的密度与其压力和温度有很大的关系。但对液化石油气主要成分的液态密度来说，温度的影响远远大于压力的影响。当温度上升时密度减小，但受压力影响却很小，可忽略不计。表2列出了液态液化石油气不同组分在不同温度下的液态密度[1]。

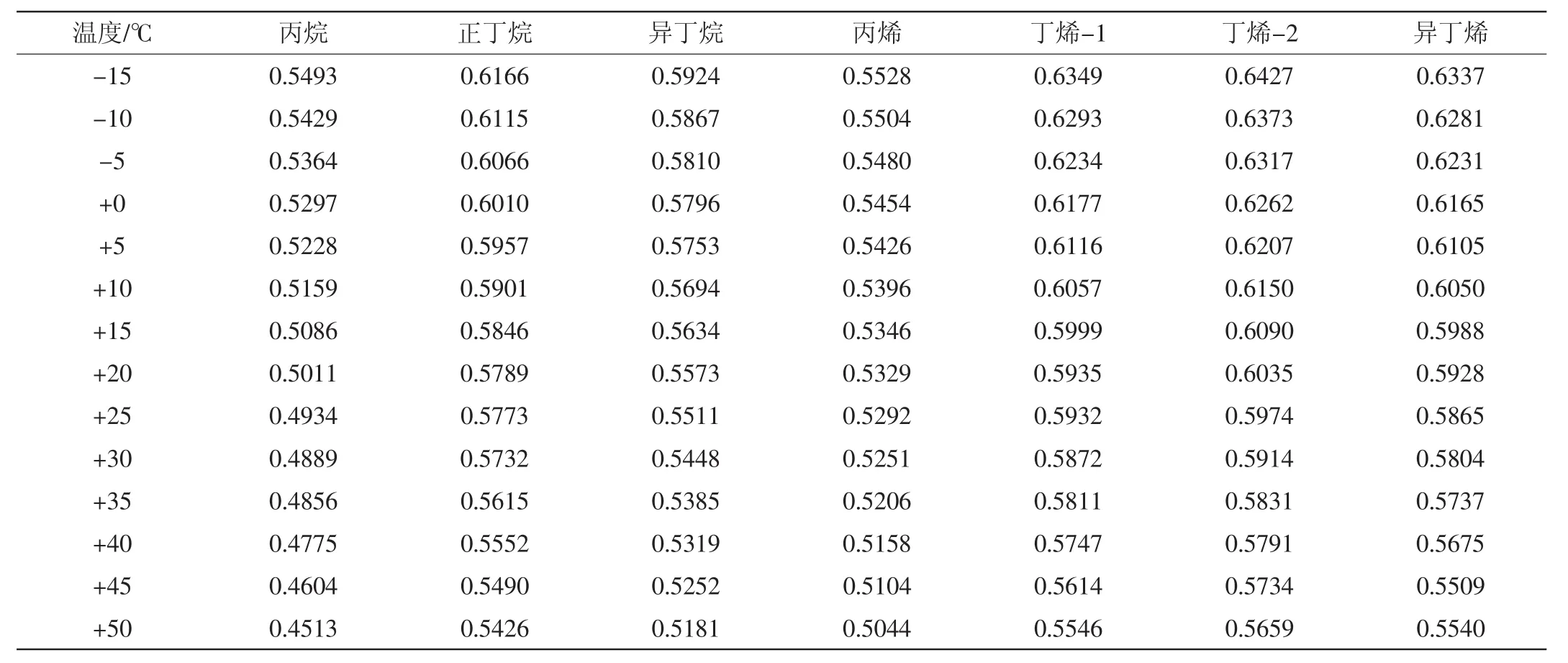
表2 不同温度下液态液化石油气的密度 kg/L

由表2可知，液态液化石油气中各类烃组分在温度的影响下，密度发生了显著的变化，温度上升，密度减小；温度下降，密度增大。

对应函数关系为：

丙烷：ρ液=-2E-07t3+8E-06t2-0.0013t+0.5283；

丙烯：ρ液=-6E-08t3-2E-06t2-0.0005t+0.5451；

正丁烷：

ρ液=-1E-07t3+3E-06t2-0.001t+0.6008；

异丁烷：

ρ液=3E-08t3-7E-06t2-0.0009t+0.5789；

正丁烯：

ρ液=-3E-07t3+1E-05t2-0.0011t+0.6164；

顺丁烯：

ρ液=1E-08t3-2E-06t2-0.0011t+0.6263；

反丁烯：

ρ液=1E-08t3-2E-06t2-0.0011t+0.6263；

异丁烯：

ρ液=-2E-08t3-3E-06t2-0.0011t+0.6169。

②气相密度。

液化石油气的气相密度是温度、压力的函数，由实际气体的状态方程P×V=n×R×T，推导出不同温度、压力下气相密度公式：

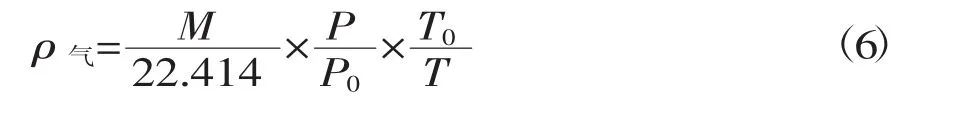
式中：P、T为饱和蒸汽的绝对压力Pa、绝对温度T；P0、T0为标准状态下饱和蒸汽的绝对压力pa、绝对温度T；M为饱和蒸汽的分子质量；

③平均密度。

密度具备可加性，因此各组分混合后的平均密度可由如下公式进行计算：

式中：ρi、ni分别为物料各组分的密度及所占混合物体积分数。

因此，混合后气-液相密度公式如下：

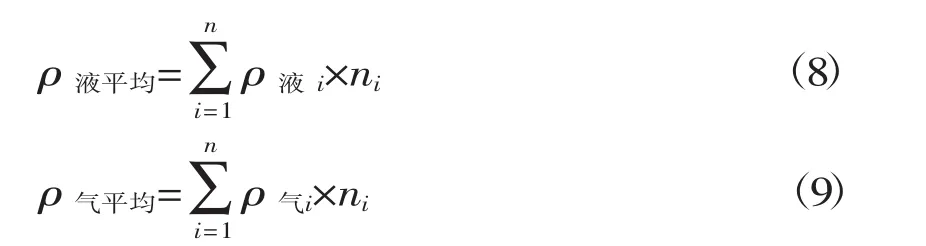
④计算结果。

对应某一温度、压力、液面计的读数下的球罐内物料质量计算如下：

式中：M液为液相质量，t；M气为气相质量，t；M总为总质量，t。

4 针对改进措施进行实例计算验证

4.1 销售丙烯验证

基础参数：储罐压力：0.54MPa；储罐内物料温度：0℃；

储罐直径：12.3m； 装车前、后液位：5.68m、5.33m。

物料各组分体积百分数见表3。

表3 丁烷化验分析数据

对比情况见表4。

表4 不同方法得到的质量对比

误差：相对误差1=M1-M2=22.15-22.04=0.11t；

相对误差2=M3-M2=21.64-22.04=-0.4t；

由数据分析验证改进方法可降低误差：1.315%。

4.2 销售液化气验证

对比情况见表5。

表5 实际销售量

误差：相对误差1=M1-M2=78.38-81.74=3.36t；

相对误差2=M3-M2=91.97-81.74=10.23t；

由数据分析验证改进方法可降低误差：8.4%。

4.3 计算结果分析

在没有对物料密度进行实际测量和对容积进行修正的情况下，通过对气液相密度及饱和蒸汽量的计算，可大大降低球罐计量误差，比较接近实际量，能够满足日常生产的需要。

5 结论

1）通过对目前球罐计量方法的误差分析和实例计算，对球罐计量数据有一个正确的认识。2）在现有的条件下，通过对球罐中物料成分的分析，温度、压力对物料密度的影响，考虑饱和蒸汽压，可以较准确地计算出球罐中物料的质量，减少计量误差。3）通过上述分析及计算为处理厂内计量纠纷、进行计量仪表比对及生产统计平衡提供了依据。通过以上分析，结合现场的具体情况，将计算过程编制可执行程序，大大减少了计算量，同时由于考虑了几个变量的可变因素，提高了计算精度。