海参糖胺聚糖催化自由基降解及其反应动力学研究
2020-06-12张培义
张培义
(华测检测认证集团股份有限公司惠州分公司,广东 惠州 516083)
海参是棘皮动物门海参纲动物,其具有补肾益精、养血润燥、温经通络等功效。海参体壁内包含酸性粘多糖类物质,其中包括海参糖胺聚糖(简称SC-GAG),其是一种类肝素抗凝剂,具有抗凝血、抑制血小板聚集、防治急性放射性损伤作用,可明显促进造血功能的恢复和增强。然而,这种从海参中提取的分子量大的糖胺聚糖存在着容易引起血小板聚集等副作用。Toshio I.等[1]的研究结果显示,低分子量的海参糖胺聚糖比未解聚的多糖在药效上具有显著的优势。低分子海参糖胺聚糖由于分子量减小,不容易被细胞外基质、血浆蛋白和细胞受体结合灭活,因此生物利用度更高。此外,低分子海参糖胺聚糖对血小板的影响减小,降低了因影响血小板功能而导致的出血合并症发生的可能性。因此,在不改变海参糖胺聚糖基本活性结构的条件下,采取适当的方法制备其低分子量的产物,已引起广大研究者的高度关注。
有研究者已采用过氧化氢法成功地实现了肝素[2]、海带硫酸多糖[3]等的降解。Ken-ichiro Y.等[4]首先应用过氧化氢解聚的方法制备得到了低分子海参糖胺聚糖,其研究结果显示,解聚前后海参糖胺聚糖的化学结构没有发生显著的变化,这证明了该法的可行性。但该法存在着反应时间较长、反应条件苛刻、工艺过程较难控制的缺点,直接给低分子产物的质量稳定性带来了风险。
本文在前人的研究基础上,把金属离子催化剂引入反应体系,采用过氧化氢降解法来降解粗海参糖胺聚糖,并针对海参糖胺聚糖的催化自由基解聚过程,结合自由基无规随机解聚的过程机制,建立反应动力学模型,并进行试验验证。提出带支链岩藻糖的糖胺聚糖的解聚反应机理过程。
1 材料和仪器
1.1 材料
海参糖胺聚糖,自制;
过氧化氢(30%,分析纯),天津富宇化工厂
三水合乙酸钠(分析纯),汕头西陇化工厂
氯化钠(分析纯),汕头西陇化工厂
乙酸锌(分析纯),天津大茂化学试剂厂
乙二胺四乙酸二钠(分析纯),汕头西陇化工厂
001×7型强酸性阳离子交换树脂,南开大学化工厂
1.2 仪器
DL-6M台式低俗大容量离心机,湘仪离心机;
DZF-6050型真空干燥箱,上海精宏有限公司;
DSK-26型不锈钢新型电热恒温水浴锅,嘉兴中新医疗仪器公司;
高效液相色谱仪Agilent technologies1200 series,Agilent;
切向流超滤仪,Millipore。
2 海参糖胺聚糖的降解反应实验方法
2.1 实验原理
过氧化氢氧化降解海参多糖的过程中过氧化氢同金属离子反应产生羟自由基OHo, 羟自由基OHo带有一个不成对的电子,性质极为活泼,易攻击破坏其临近的海参糖胺聚糖大分子,使其降解。
以某金属阳离子Mn+为例羟自由基产生过程为[#5]:
Mn++ H2O2→Mn+1++OH·+ OH-
Mn++ OH· →Mn+1++ OH-
Mn+1++ HOO·→Mn++ H++O2
2. 2 实验过程
分别取5g海参糖胺聚糖,加入200mL水溶解,加入终浓度为0.5mol/L氯化钠,0.5mol/L三水乙酸钠,以10mL/h的速度滴加浓度为10%的过氧化氢20 mL,加入1mL浓度为1mol/L的乙酸锌为催化剂,分别于25,35,45,55℃水浴中反应,反应过程中pH值控制在7.5左右。每组实验分别于20,40,60,80,100,120min取样,求得每组不同时间降解产物的分子量,考察催化自由基降解反应动力学。
3 动力学模型的建立
通过对海参糖胺聚糖解聚前后的红外光谱数据、单糖分析结果以及核磁数据结果的比较分析发现,支链岩藻糖在解聚过程中没有发生明显的脱落,三个单糖的摩尔比也没有发生显著的变化,因此,我们有理由认为海参糖胺聚糖中的β-D-葡萄糖醛酸(1→3)-硫酸酯化-β-D-N-乙酰氨基-半乳糖和硫酸酯化-β-D-N-乙酰氨基-半乳糖(1→4) β-D-葡萄糖醛酸中的糖苷键在断裂的机会上是均等的,并且硫酸酯化-α-L-岩藻糖(1→3)- β-D-葡萄糖醛酸的糖苷键不被断裂。
从而,可以假设海参糖胺聚糖的自由基解聚满足无规解聚过程,则定义:
α=s/(N。-1)
(1)
式中:s为因水解而断裂的键数,N。为海参糖胺聚糖的初始聚合度,a为大分子中每一缩醛键在某一确定时刻的裂解几率。假设海参糖胺聚糖降解是单分子反应,则降解速率ds/dt与未断裂的缩醛键数成正比,即:
ds/dt = k(N。- 1- s)
(2)
积分得:
s = (N0-1)[1- exp(-kt)]
(3)
式中:s 与 a 是解聚进行时间为t时的断键数目和降解程度;k为水解速率常数,所以:
a = 1- exp(- kt)
(4)
在时间t时,水解系统的平均聚合度为Nn ,起始聚合度为N。,则:
Nn=N。/(s+1)
(5)
合并式(3)和式(5),消去s 得:
(Nn-1)/Nn=(N0- 1)/No·exp(-kt)
(6)
等式两边分别取对数,则得:
ln[Nn /(Nn - 1)]=-ln[N。/(N。-1)]+kt
(7)
以ln[Nn /(Nn - 1)]对 t 作图,应为直线关系,直线的斜率为k。根据Arrhenius公式[6],则有
k=Aexp(-E/RT)
(8)
式中:A 是经验常数,E是降解反应的表观活化能,T是热力学温度,R是理想气体常数,两边取对数,可以得到:
lnk=lnA-E/RT
(9)
用lnk对-l/RT作图,即可求出反应的活化能。
4 动力学模型的试验验证
根据式(7)以ln[Nn /(Nn - 1)]对t作图,结果见图1。由图2所示,在实验温度下,ln[Nn /(Nn - 1)]与 t呈线性关系。
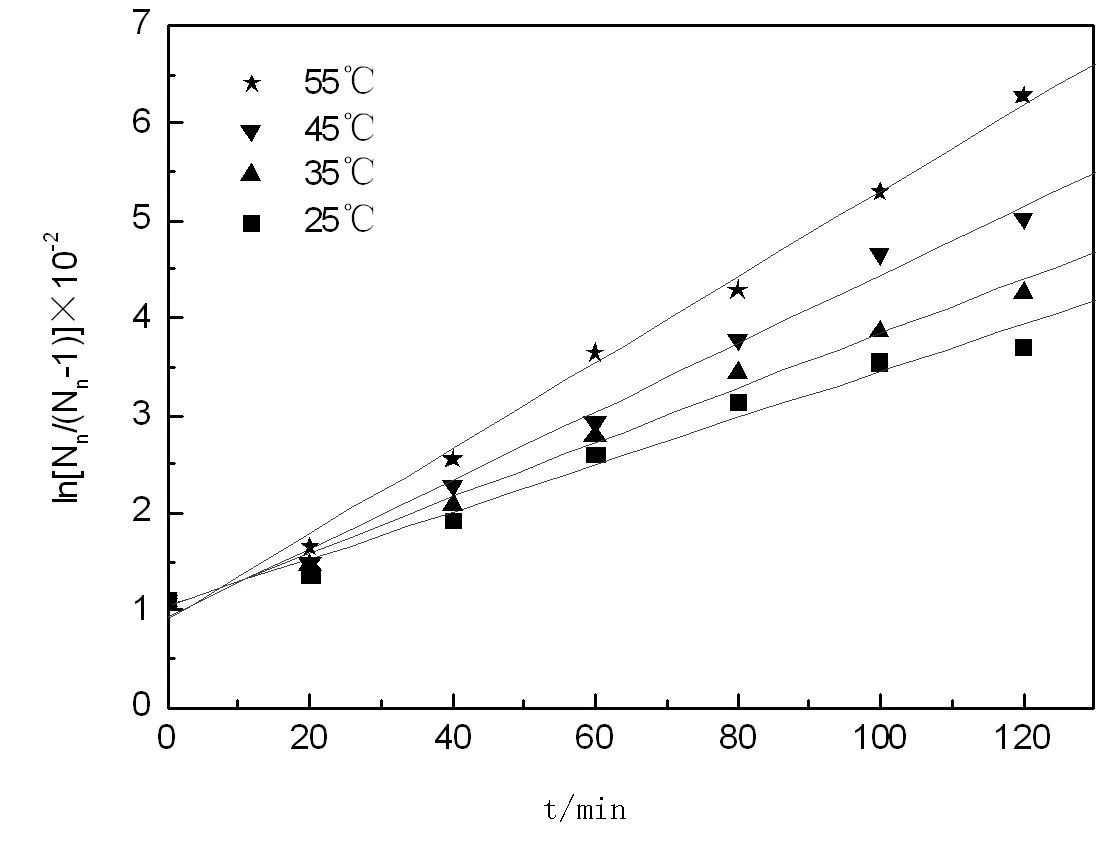
图1 不同温度下ln[Nn/(Nn - 1)]与t的关系曲线Fig.1 Relationship curve of ln[Nn/(Nn - 1)] and t in different temperature
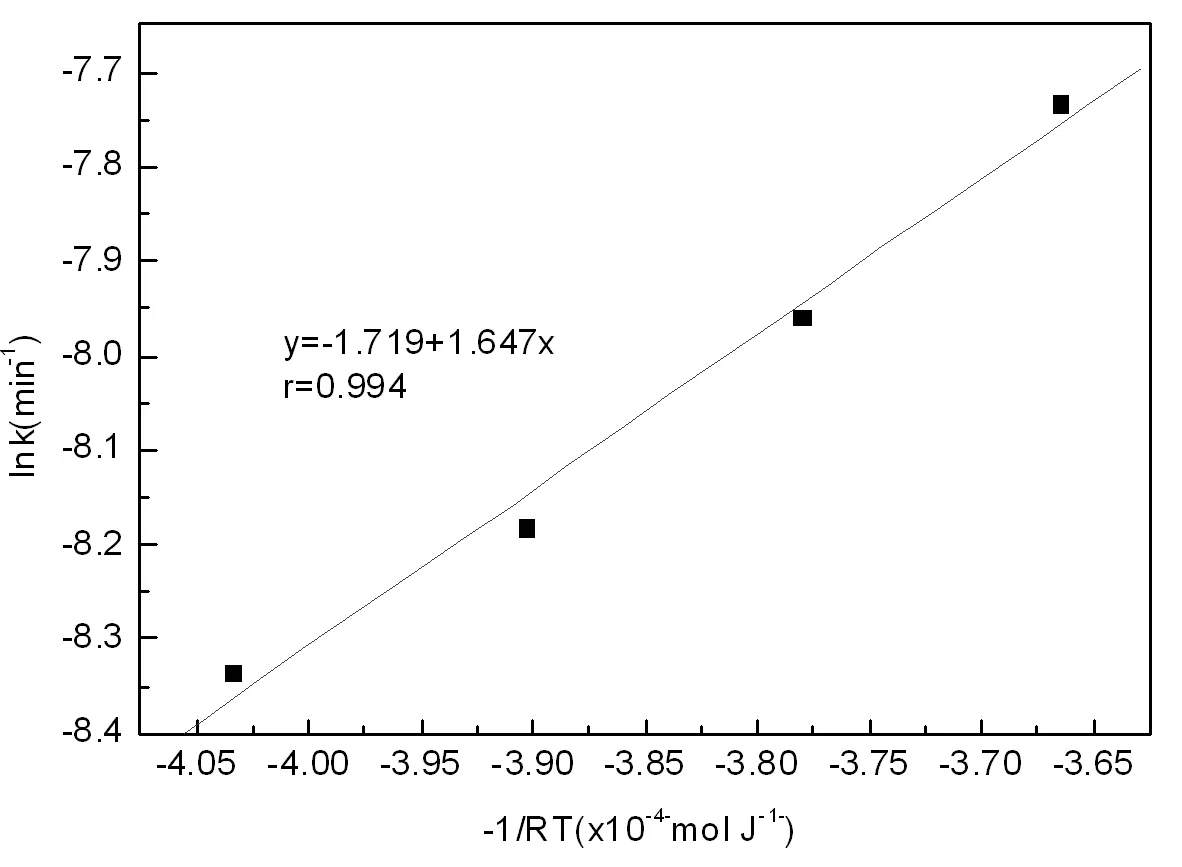
图2 lnk与-1/RT的关系曲线Fig.2 Relationship curve of lnk and -1/RT
对不同温度下ln[N /(N -1)]-t曲线,进行线性回归所得直线的斜率即为k值,结果见表1。由表1可见,其回归系数均在0.989以上,说明在实验范围内,糖胺聚糖的降解较好地符合无规降解过程。此外,随着温度的升高,降解的表观速率常数逐渐增大。

表1 不同温度下所得k值与R值Tab.1 Result of k and R in different temperature
根据式(9)以lnk对-1/RT作图,结果见图2。由图2中直线的斜率便可得到海参糖胺聚糖降解反应的活化能E为16.47kJ/mol,回归系数为0.994。回归系数较高。因此,通过试验验证糖胺聚糖的降解较好地符合无规降解过程。并在该基础上求得海参糖胺聚糖降解反应的活化能E为16.47kJ/mol。
