基于DIC技术的地下软土内部激振影响区试验

殷德顺，赵义东，白鹏翔，谢晶鹏

(河海大学力学与材料学院，江苏 南京 211100)

1978年改革开放以来，中国交通基础建设取得巨大成就，但要注意到其中很多已建成的地铁隧道、高铁隧道和桥梁都被长期沉降灾害所困扰[1-2]。总结分析相关长期沉降灾害能够发现：(a)灾害多发生于地下软土层；(b)长期沉降多由列车运行产生的振动荷载引起[3]。列车振动影响范围内各部位土体的动力响应不同，力学行为变化情况也不同，探究内部激振在地下软土中的传播行为具有重要意义。

目前，许多学者针对软土在振动条件下的复杂力学特性进行了大量研究。Wang[4]、程学磊等[5]运用振动台试验模拟研究地震作用下软土的动力响应和特性变化，Yang等[6]运用振动台试验研究了在剪切和机械振动荷载作用下砂质和黏性床层沉积物的流变特性，黄珏皓等[7]运用动三轴试验仪模拟研究循环荷载下软黏土的孔压变化情况，殷德顺等[8]利用拖球试验探究不同条件下的地下软土流变特性。可以发现室内试验多数关注整体振动或某一土体单元的力学行为，对于地下软土的内部激振行为研究较少。而相对于整体振动，研究内部激振时缺乏相应的试验装置，有必要针对地下软土内部激振设计新型试验装置来探究其具体行为。

潘昌实等[9]利用有限元法对黄土隧道进行了列车振动响应数定分析，Sheng等[10]、王铁生等[11]建立了预测模型计算地铁隧道的动力响应和沉降问题，曾晨等[12-13]以解析方法研究了饱和土体中隧道在列车振动荷载作用下的动力响应。马险峰等[14]采用数值模拟的方法研究了地铁列车运行时盾构隧道及其周围土体的动力响应问题。刘涛[15]、袁金秀等[16]通过现场实测对交通荷载下地面振动的传播与衰减特性进行研究。上述是针对列车运行时的振动响应进行模拟研究，但由于理论解析、数值模拟对于复杂的地下软土只能简化处理，现场实测受技术水平和工程环境所限，多研究地表振动规律，仍难以准确反映地下软土中的振动传播规律。地下软土较为复杂，振动行为受所处埋深、土壤含水率、振动频率等因素的影响，而对内部激振在地下软土中的传播规律和影响区域尚无明确的结论。

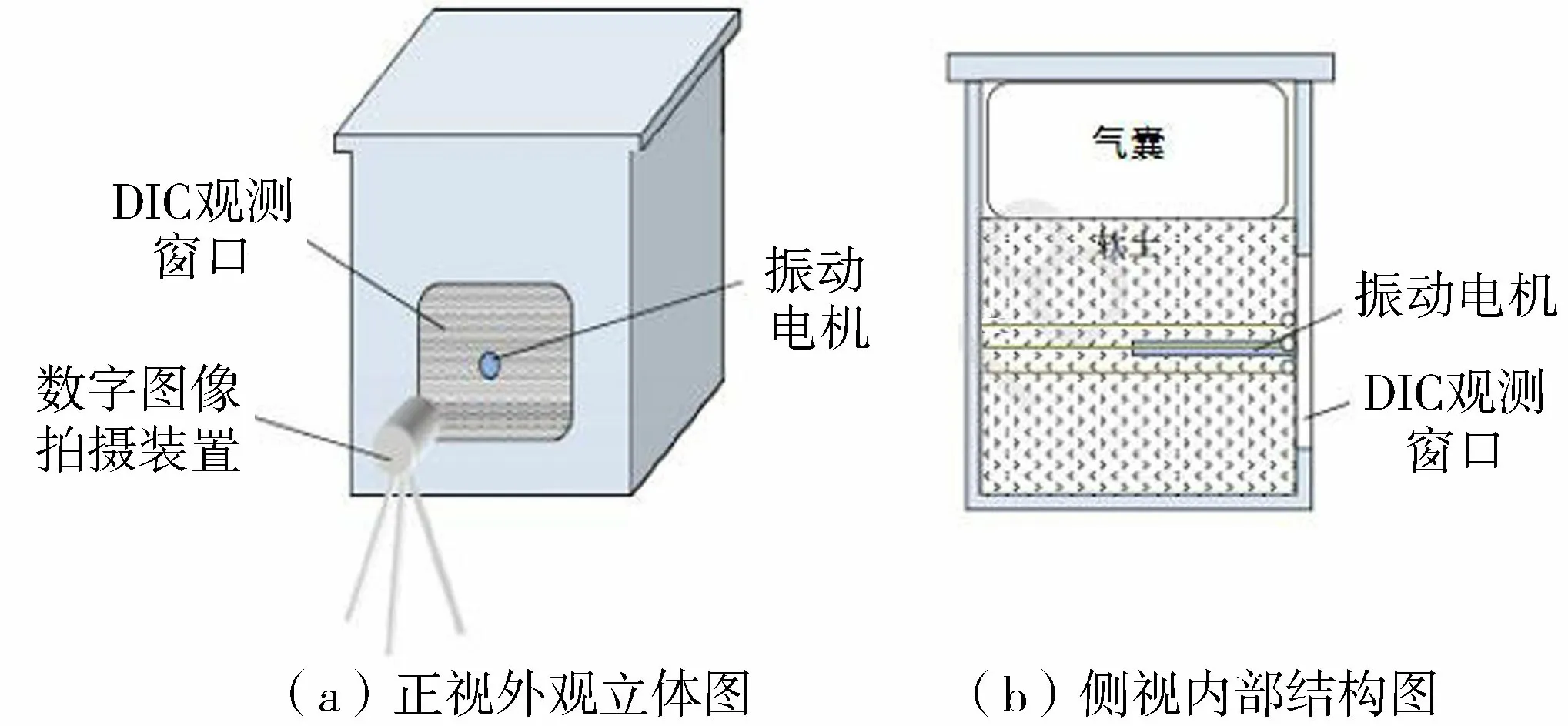
图1 内部激振试验装置示意图Fig.1 Schematic diagram of internal excitation test device

图2 可调频振动电机和高速相机Fig.2 FM vibration motor and high-speed camera

随着科技的发展，数字图像相关(digital image correlation，DIC)技术已渐渐进入岩土力学学者的视线。数字图像相关技术通过比较物体表面变形前后的数字图像，直接获取位移和应变，可以从多方面展现细观变化信息。近年来，数字图像相关技术已被应用于观察土体受外荷载时颗粒的运动变化和应变场演变规律[17-22]。因此，用DIC技术观测模拟环境中地下软土的振动变形情况不失为一种有效的研究手段。

本文引入DIC技术开发地下软土内部激振响应瞬时光学测量系统，以不同围压、不同振动频率模拟内部激振条件下的地下软土环境，并观测土颗粒运动情况。土颗粒运动的幅度既是土体力学行为的反映，也是振动衰减的反映，以此刻画内部激振影响区和振动衰减规律。

1 试验装置与试验安排

1.1 试验装置

为了观测地下软土的内部激振行为，特设计内部激振试验装置模拟地下软土的振动环境，并引进二维数字散斑相关测量系统进行全场细观测量，开发了基于数字图像技术的地下软土内部激振响应瞬时光学测量系统，装置示意图如图1所示。装置主要由试验容器、加压气囊、土压力计、可调频振动电机、高速相机、相机固定架、白光光源、电脑等构成。

设计试验容器时,为便于相机采集软土动态变形图像，添加透明玻璃窗口进行可视化改装改造(图1)，实现与图像采集系统进行合理衔接。容器内部尺寸418mm×418mm×571mm，观测窗口尺寸250mm×250mm。加压气囊用来给土体加压，模拟不同埋深的地下环境。可调频振动电机和高速相机如图2所示。可调频振动电机用来模拟不同的振动情况，振动频率可调范围为0～60Hz，不同振动频率对应不同的振动力，60Hz时对应激振力为250N，最大功率为40W。相机为AOS高速相机。试验过程中，采用高速相机记录振动过程中软土的细观运动状态。

1.2 试验安排

试验用土是在南京市江宁区牛首河河床采集到的土样，其力学性质较符合软土的要求。铲出的淤泥，经过暴晒风干、烘干、粉碎、过筛、加水搅拌等处理，得到均匀无固结的44%含水率土样。测定并记录土样的基本物理指标，具体如下：液限为31.3%，塑限为20.1%，塑性指数为11.2，干密度为1.52g/cm3，最大动弹性模量为35.5MPa，阻尼比为16%。

本试验采用黑白喷漆人工喷制散斑对软土进行处理，便于数字图像测量系统根据试样表面的光强变化跟踪并获取颗粒的变形信息。试验时，放置好土样和振动电机后，用气泵调节土压力，打开DIC图像采集系统，启动振动电机，进行试验数据采集。分别在土压力为1kPa、25kPa、50kPa、75kPa、100kPa、125kPa时进行试验，每一围压下将振动电机频率调节到5Hz、10Hz、20Hz、30Hz、40Hz，进行共计30组试验。相机采样频率为500帧/s，实时观测并采集振动过程中土颗粒的运动变化。

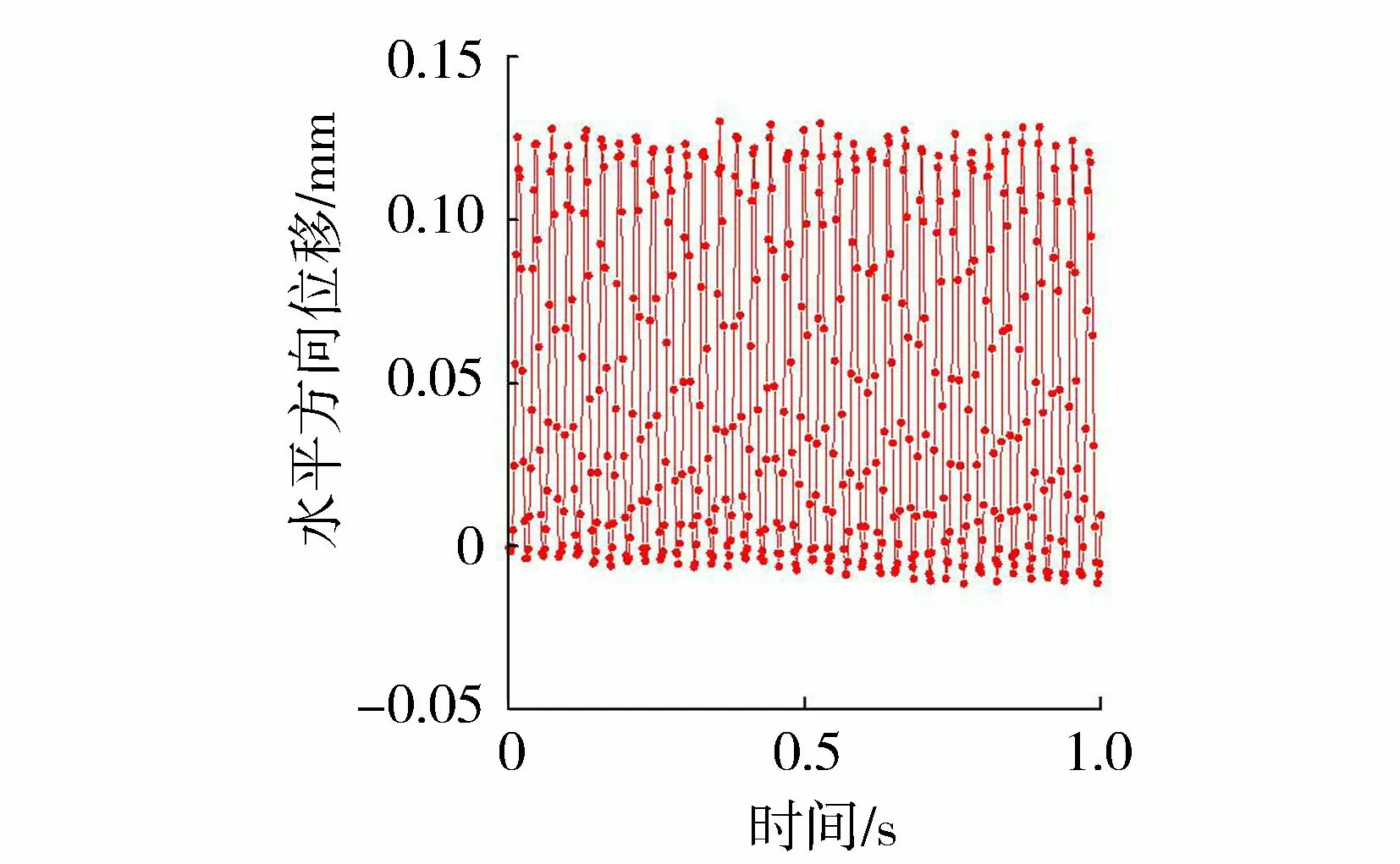
图3 某一条件下振动过程中一点处的位移随时间变化曲线Fig.3 Relationship between displacement and time at a point in the process of vibration under a certain condition

本试验拍摄时选择玻璃窗右下方1/4区域，实际采集区域大小为 130 mm×130 mm。由获得振动过程的连续数字图像，通过数字图像相关分析软件处理，可得到试样在内部激振过程中不同时刻的位移场、应变场和速度场等信息。

为了衡量内部激振对地下软土的影响程度，选取土颗粒的振动幅度来讨论衰减规律和影响区。对位移图进行标记取点、数据提取。以观测窗口中心为原点，在水平向右、竖直向下、斜下45°方向上等距取点，并提取点位的位移数据，分析具体点位的运动规律。图3给出了某一条件下振动过程中一点处的位移随时间变化曲线，可以看到土颗粒在振动电机激励作用下做简谐运动。以点位的位移数据中稳定有效的位移最大值减去位移最小值，即得到该点位处的振幅。

早在上世纪六七十年代，各种传统艺术形式被打破就已初见端倪，随着时代的变迁，艺术的范围开始慢慢扩展到生活中的方方面面，艺术和生活的界限正在消融。同一时期，苏珊·桑塔格发表了《反对阐释》一文，苏珊·桑塔格式的形式美学问世了。

2 试 验 结 果

2.1 振幅与距振源距离的关系

众所周知，振幅会随着距振源距离的增大而衰减，但在不同情况下的具体衰减规律尚不明确。选取不同情况下的振幅随距振源距离变化曲线，对它们之间的关系进行探究。图4给出了围压为1 kPa时，振动频率分别为20 Hz水平向右方向和振动频率40 Hz竖直向下方向的振幅。图5给出了围压为125 kPa，振动频率分别为5 Hz、40 Hz时竖直向下方向的水平方向振幅和竖直方向振幅。

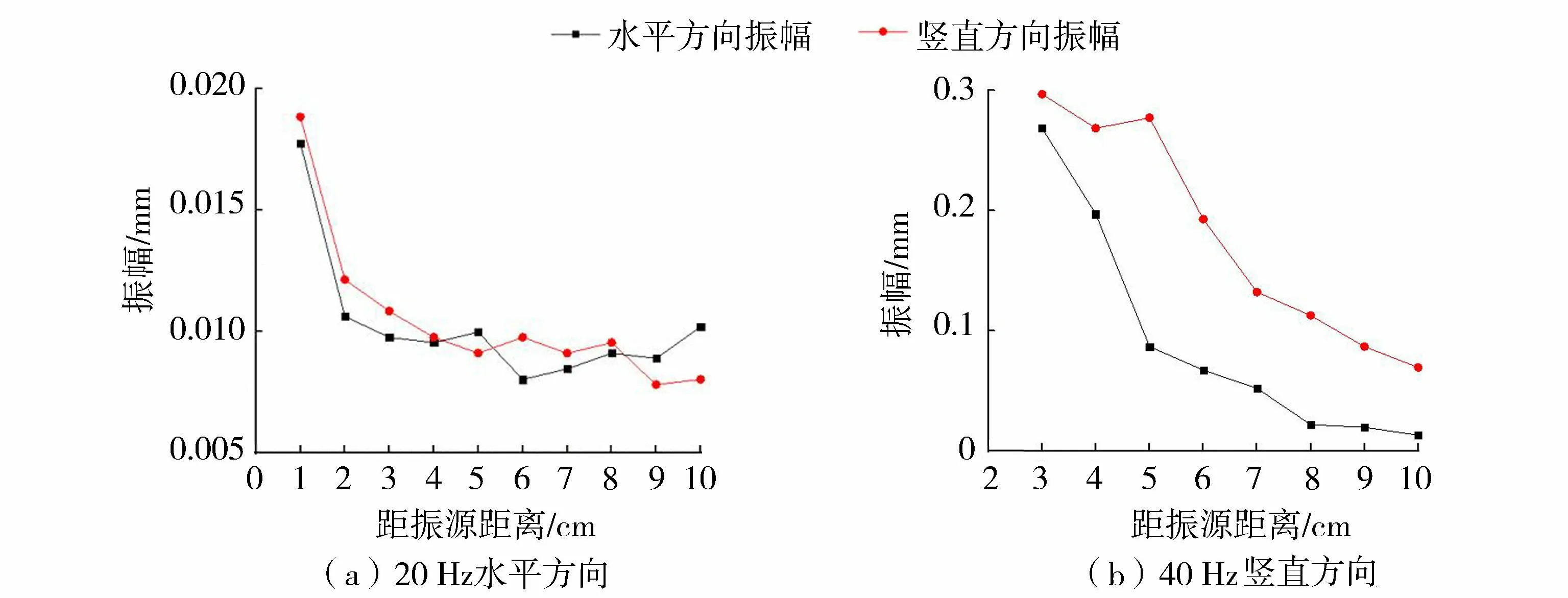
图4 围压为1 kPa时水平和竖直方向振幅Fig.4 Horizontal and vertical amplitude under confining pressure of 1 kPa

从图4、图5可以看出：在振源近处振幅最大，受振动频率影响，振幅最大值相差较大；而随着距离的增大，振幅迅速减小。以图5(b)为例，到达距振源距离为5 cm处，振幅衰减幅度超过80%，超过这一距离后振幅衰减变得缓慢。试验结果显示，随着距振源距离的增大，水平和竖直方向振幅均先迅速减小，到一定距离后振幅缓慢减小。即随着距离增大，受土体几何阻尼和材料阻尼影响[23]，能量迅速衰减，表现为土体振幅的迅速减小。

2.2 振幅与振动频率的关系

从2.1节可以发现振动频率对于振幅有着很大影响，具体表现为低振动频率和高振动频率下的振幅表现有很大不同。对不同振动频率下的某一指定距离或区域处的振幅进行比较，分析振幅和振动频率之间的关系。图6为围压125 kPa时3个点在不同振动频率下的水平方向振幅。为了抵消计算单个点位振幅带来的不稳定性，特地选取某一指定区域内振幅平均值来进行比较。图7给出了不同围压、不同振动频率下一指定圆形区域内的竖直方向振幅平均值，该区域是以斜下45°方向距振源6.4 cm处为圆心，半径为15 mm的圆形区域。

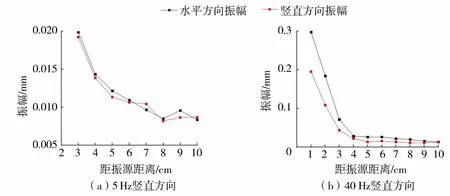
图5 围压为125 kPa时水平和竖直方向振幅Fig.5 Horizontal and vertical amplitude under confining pressure of 125 kPa

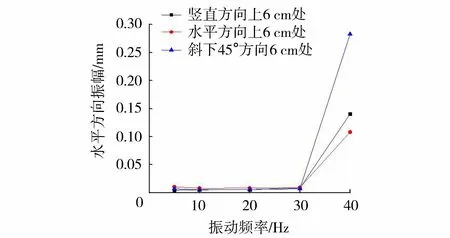
图6 125 kPa时3个点的水平方向振幅Fig.6 Horizontal amplitude of three points under confining pressure of 125 kPa

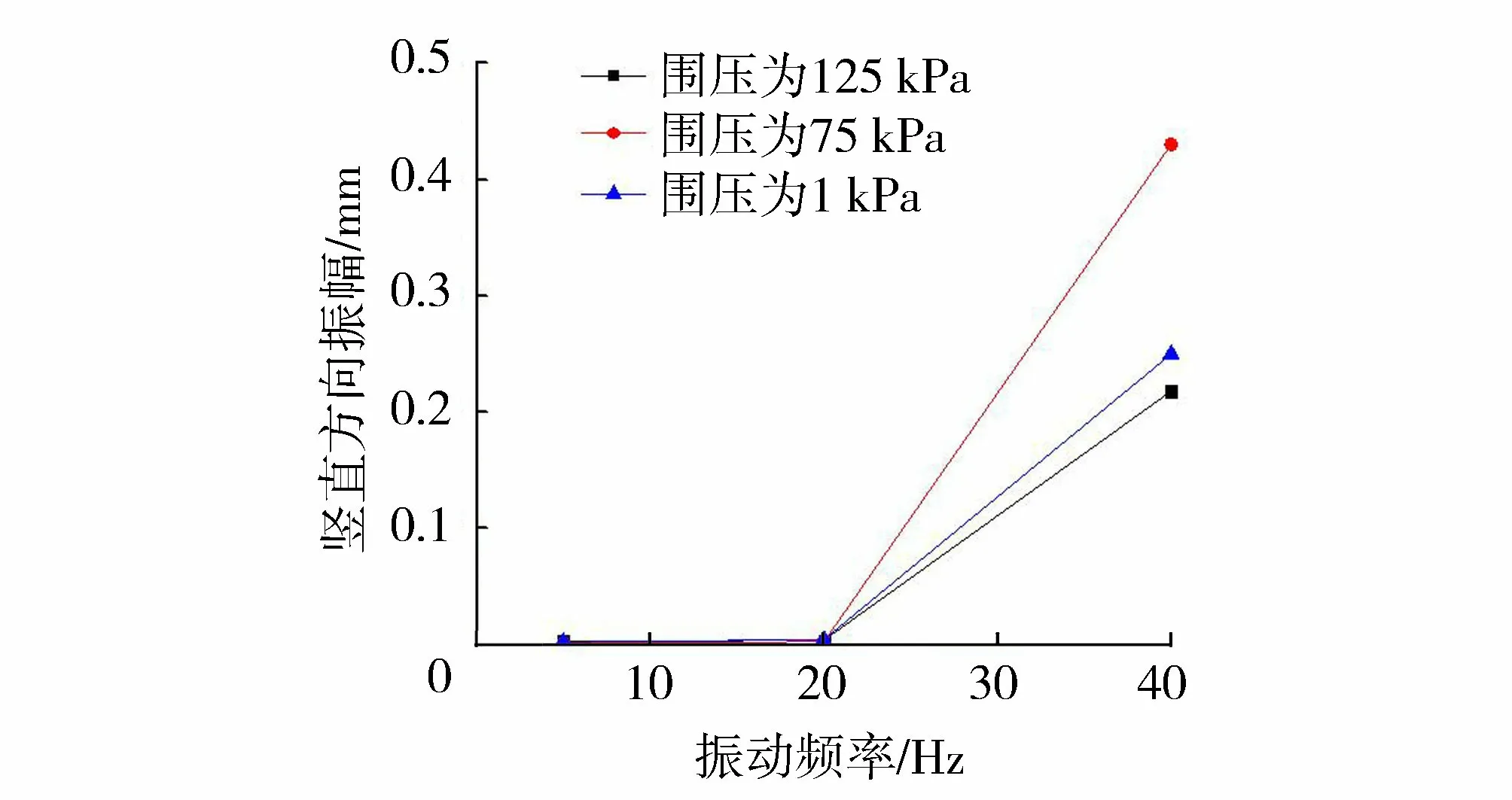
图7 不同围压时一指定区域处的竖直方向振幅Fig.7 Vertical amplitude at a specified area under different confining pressures

从图6、图7可以看出：125 kPa围压下，3个方向上距振源6 cm处的振幅均随着振动频率增大而增大，在5～30 Hz时振幅增大缓慢，到40 Hz时振幅增大迅速；在1 kPa、75 kPa围压下，也存在类似情况。总结发现，随着振动频率增大，振幅在中低频率时缓慢增大，超过一临界振动频率时振幅迅速增大，该临界值在30～40 Hz之间。本试验中振动电机的振动力随着振动频率的增大而增大，即振动力增大到一临界值时，土体在激振作用下产生较大响应，这一临界是土体状态发生变化，由固向流转变的标志。

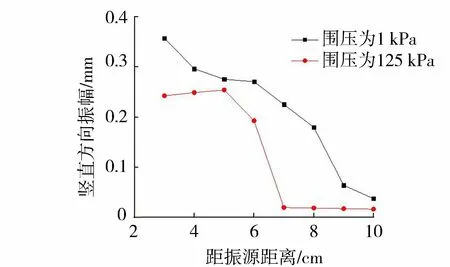
图8 40 Hz不同围压时斜下45°方向点位的竖直方向振幅Fig.8 Vertical amplitude in the obliquely downward 45° direction at 40 Hz under different confining pressures

2.3 振幅与围压的关系

在实际工程中，土体埋深对土体特性的影响很大，本试验选用不同围压来模拟不同埋深，观测围压对于软土内部激振行为的影响。经过计算，单一点位和某一指定区域的振幅与围压的关系无明显规律，考虑用不同围压下振幅在某一方向上的变化曲线探究围压对于振幅的影响。图8给出了围压为125 kPa和1 kPa、振动频率为40 Hz时，斜下45°方向上点位的竖直方向振幅。

从图8可以看出，在距振源3～6 cm处，125 kPa时的振幅略小于1 kPa时的振幅；距振源7 cm处，125 kPa时的振幅迅速降到0.020 mm，而1 kPa时的振幅仍保持在0.225 mm，并在距振源10 cm处才减小到0.037 mm，即1 kPa时振动引起的振幅区域更大。结果表明，随着围压的增大，振源近处的振幅轻微减小，而受内部激振影响较大即振幅较大的区域显著减小。

3 内部激振影响区分析

影响区域受围压影响，但全场受到的影响尚不明确。为了更加直观地了解内部激振对于地下软土的影响范围和影响程度，基于DIC技术，在已知全场振幅的基础上引入内部激振影响区。将某一处的水平方向振幅和竖直方向振幅的平方和的算术平方根作为衡量振动对于该处土体振幅的影响量s，即

(1)

在图像采集区域内取点，计算每个点位的s值，绘制出土体内部激振影响区。图9给出了不同围压和振动频率下的土体内部激振影响区域。从图9可以看出：(a)振动频率为5 Hz时，在整个影响区域内振幅很小，衰减缓慢甚至有所波动；振动频率为40 Hz时，影响区域内振幅较大且衰减迅速。(b)当振动频率为40 Hz时，1 kPa围压下s≥0.340 mm的区域面积约为5 500 mm2，125 kPa围压下此面积约为2 100 mm2，前者远大于后者(以s≥0.34 mm计算受振动影响较大的区域)。此外，1 kPa围压下的振动影响区中约有1 400 mm2的区域的s≥0.433 mm，而125 kPa围压下没有s≥0.433 mm的区域。试验结果表明：随着振动频率的增大，土体所受的影响程度显著提升；随着围压的增大，土体所受的影响程度减小，受振动影响较大的区域显著减小。

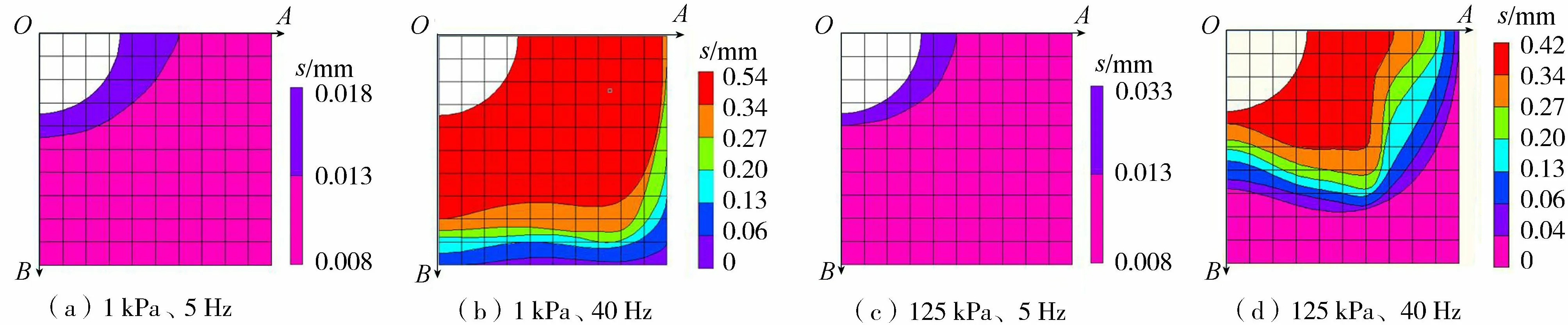
图9 不同情况下的土体内部激振影响区域Fig.9 Schematic diagram of the local vibration affected zone of soil under different conditions

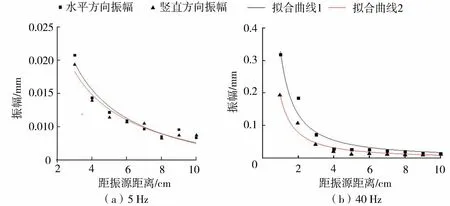
图10 围压为125 kPa，不同振动频率下竖直向下方向振幅曲线Fig.10 Horizontal and vertical amplitude in the vertical downward direction under different vibration frequencies under confining pressure of 125 kPa

内部激振影响区给出可以更加直观地表述内部激振对于土体的影响，从中得出的结论可以和前面总结的相印证。从图9(b)、图9(d)可以看到，在斜下45°方向上，振幅等值线有一个凸出部分，即内部激振对此区域的影响大于其他方向上等距离的区域，振动传递存在方向差异性。

4 振幅衰减曲线分析

在2.1节指出振幅衰减多为先迅速衰减，后缓慢衰减，对振幅衰减的具体形式进行了深入分析。图10给出了围压125 kPa，不同振动频率下竖直向下方向上水平、竖直方向振幅曲线，并对变化曲线进行多种函数的拟合，经比较幂函数y=axb拟合效果较好。围压125 kPa、振动频率5 Hz时，水平方向振幅曲线拟合为y1=0.041 0x-0.797 0，R2=0.934 2，竖直方向振幅曲线拟合为y2=0.040 7x-0.731 9，R2=0.928 3。同样，振动频率为40 Hz时，水平方向振幅曲线拟合为y1=0.329 3x-1.297 2，R2=0.954 5，竖直方向振幅曲线拟合为y2=0.200 7x-1.299 9，R2=0.963 3。

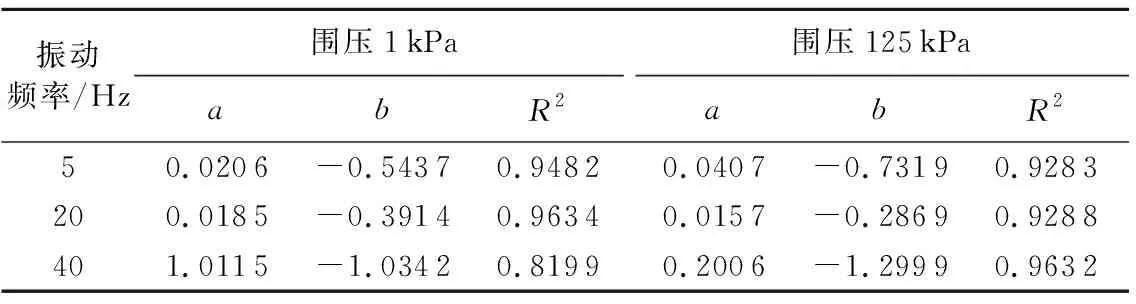
表1 以y=axb拟合竖直向下方向的竖直方向振幅衰减曲线得到的参数a、bTable 1 Parameters a, b and R2 of vertical amplitude attenuation curve in vertical downward direction under different conditions

从以上拟合结果可以看出，幂函数y=axb对于振幅衰减曲线拟合效果较好。对更多实验数据进行拟合，探究参数a、b的取值情况，汇总不同情况下竖直向下方向竖直方向振幅衰减曲线，结果见表1。由表1可知，参数a、b与围压和振动频率满足以下关系：中低频率时，a和b的值都较小，随着振动频率增大，a和b的值都增大；在高频率时，随着围压增大，a值减小。因此，振幅衰减曲线可以用如下形式拟合：

A=axb

(2)

式中：A——振幅；x——距振动源距离；a、b——参数，与振动频率、围压等因素有关。

5 结 论

a. 把基于数字图像相关方法的光学测量技术与软土内部激振试验相结合，通过可视化改造，开发了基于数字图像的软土变形细观测量系统，实现了对软土土体全场实时测量。对全场振幅的准确测量，表明了该测试方法的合理性和有效性。

b. 随着距振源距离的增大，水平和竖直方向振幅均先迅速减小，到一定距离后，振幅缓慢减小。随着振动频率增大，振幅在中低频率时缓慢增大，超过一临界振动频率时，振幅迅速增大，该临界值在30～40 Hz之间。随着围压的增大，振源近处的振幅轻微减小，而受内部激振影响较大即振幅较大的区域显著减小。

c. 通过全场测量得到的内部激振影响区更加直观、准确，可以表征出影响区域和影响程度。随着振动频率增大，土体所受的影响程度显著提升；随着围压增大，土体所受的影响程度减小，受振动影响较大的区域显著减小。

d. 振幅衰减曲线较符合幂函数y=axb形式，a和b与振动频率、围压等因素关系密切：中低频率时，a和b的值都较小，随着振动频率增大，a和b的值都增大；在高频率时，随着围压增大，a的值减小。