基于前测，把握课堂——以“两位数乘两位数（不进位笔算）”为例

福建省福州金山小学 林希光

《义务教育数学课程标准（2011 年版）》指出：数学活动应该建立在学生认知发展水平和已有的知识经验的基础之上。教师的教学行为只有建立在真正了解学生的认知基础、正确把握学生的探究起点上，教学才能真实而有效。前测是用于了解学情的一种重要手段，然而，如何根据前测的结果改变教学策略、设计合乎学情且具有实效性的教学过程？今天，笔者借“两位数乘两位数（不进位笔算）”一课的磨课过程，谈谈如何基于前测结果有效把握课堂实施。

一、基于前测结果，把握教学起点

俞正强老师在《种子课》一书中曾说：“教师选择学生学习认知的现实起点，有利于培养学生形成以交流与研究为特征的学习方式。”可见，学生起点的把握至关重要。很多教师在备课时，虽然也预设了学生可能存在的不同的认知差异，可是这种预设往往源自教师的经验和想象，带有明显的主观性，与学生的真实情况存在一定的偏差，甚至是误解。而根据前测结果探寻到的学生的起点更加客观且有说服力。

在“两位数乘两位数”的第一轮教学中，新课伊始，笔者以四组口算题复习引入（具体如图1），一来回顾旧知，二来让学生通过观察发现每个两位数都可以拆成一个整十数与一个一位数的和，为后续的“转化”做好铺垫。

图1

然而，在后续自主探究“14×12”的计算方法时发现，几乎所有学生都采用了将12 拆分成“10 和2”的形式，方法单一。没有多元的算法，就无法体现出该方法的优越性，教师的强势铺垫又剥夺了学生自主探索解决问题方法的权利，影响了学生探究经验的获取，不利于核心素养的培植。

产生这种现象的原因必是受到口算铺垫的影响。然而，如果舍弃口算，学生能否想到将其中的一个两位数拆成整十数和一位数进行计算呢？基于这样的疑问，笔者对三年级下册还未学习该课时的学生进行了前测。

前测内容（1）：想办法计算出24×12 的积。

前测对象：三年级两个班共103 名学生。

前测结果：

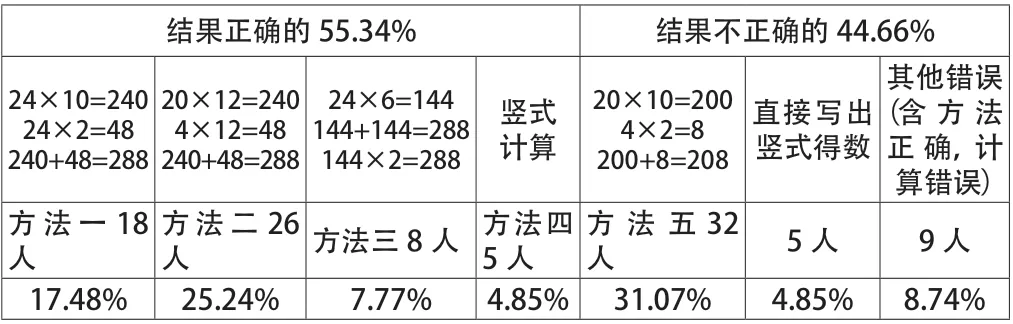
结果正确的55.34% 结果不正确的44.66%24×10=240 24×2=48 240+48=288 20×12=240 4×12=48 240+48=288 24×6=144 144+144=288 144×2=288竖式计算20×10=200 4×2=8 200+8=208直接写出竖式得数其他错误（含方法正确，计算错误）方法一18人方法二26人方法三8 人 方法四5 人方法五32人5 人 9 人17.48% 25.24% 7.77% 4.85% 31.07% 4.85% 8.74%

前测结果发现，在无任何铺垫的情况下，超过40%的学生都能将其中的一个两位数转化成整十数和一位数进行计算（如方法一与方法二），这种现象缘于学生在本单元的一、二课时刚刚学习完该内容，对两位数乘一位数和整十数的计算方法十分熟悉。笔者课前认为学生需要在课前进行口算复习，并且设计“24×2、24×10”这样一组口算来降低探究难度的想法实属画蛇添足，反倒将学生的思维禁锢在 “12=10 ＋2”的单一方法中，不利于探究结果的对比和优化，不利于学生思维灵活性和策略多样性的培养。

基于前测结果，笔者果断舍弃口算，为学生争取了更多自主探究与交流讨论的时间。第二轮教学时，学生在原认知的基础上自主探索计算方法，学生的创造性思维被充分调动，算法纷呈，为后续交流、讨论与优化算法提供了充足的素材与经验支持。

二、根据前测情况，甄选教学素材

前测能让教师读懂学生的内心倾向，了解学生的实际需求。符合学生心理特征的学习内容可以激发学生的学习欲望，得心应手的学习材料能够帮助学生快速有效地进入探究学习的状态。本节课中，对算理直观理解的素材选择上，笔者也经过了一番思考。

第一轮教学时，笔者根据教材安排，选择使用点子图进行教学。当学生利用点子图探究“14×12”的计算方法后，笔者发现有一部分学生选择将“每套14 本”中的“14”拆成“10 和4”，然而在点子图中表达时（如图2）却说不清道理。通过采访了解，学生眼中的一套书14 本是每份数，本应是一个整体，分割后每个部分分别乘12 表示的意思，表达起来比较困难。虽然这种方法能正确地计算出结果，却无法表达出计算过程每一步的含义，一定程度上影响了学生对计算算理的理解。

图2

那么，是否可以将点子图更换为无法将每份量进行拆分的实物图？学生内心更倾向选择哪一种直观图帮助思考与表达？针对这个问题，笔者进行了第二次前测。

前测内容（2）：想办法算出“14×12”的积，写出你的思考过程，并把想法分别在两幅图（如图3）中圈一圈，你更喜欢哪一幅图来帮助思考？

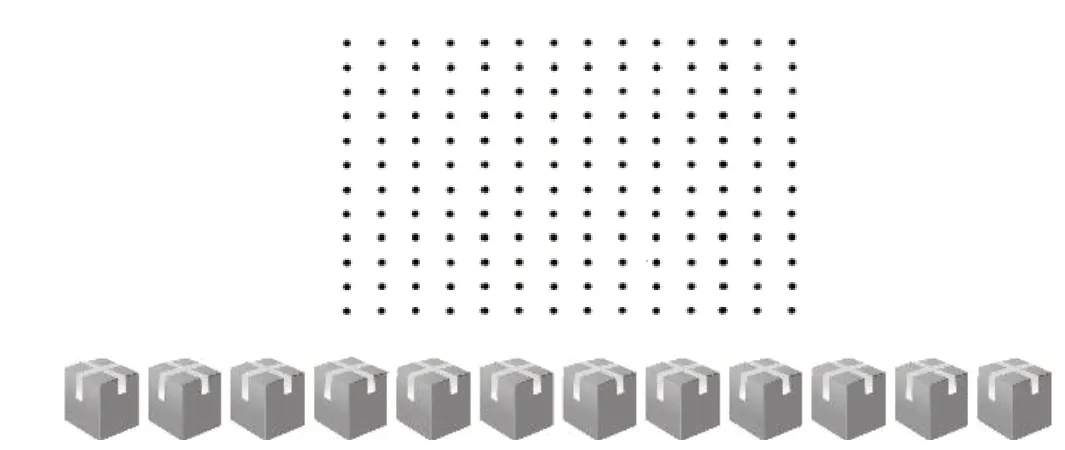
图3

前测对象：三年级抽样选取好、中、弱学生各2 名。

前测方法：将6 名学生随机分为2 组。一组先在点子图上圈，再在实物图上圈；另一组先在实物图上圈，再在点子图上圈。

前测结果：学生圈实物图的速度更快一些。其中4 名学生算式和图所表示的意思相同，结果完全正确，基本能结合图讲出算理。另外2 名学生算式正确，点子图错误，一个是数错行，一个是图上圈的方法和算式表达的意思完全不同。

笔者发现，学生无一例外地倾向选择实物图帮助计算。在学生眼中，实物图能更清楚地表达出14 和12 所代表的不同的量。14 为每套书的本数，是每份数，是一个整体不可拆分，而12 是书的套数，是份数，可以拆成“2 个6 套、3 个4 套、6 个2 套”，或者是“10 套+2 套、5 套+7 套” 等形式，符合学生的生活经验。用实物图更便于进行算理的表达，“14 乘几”也就是“几个14”，也就表示“几套书的本数”，对应的数量关系清晰，符合学生的顺向思维。实物图数量简单，图形形象，更贴近三年级学生的心理特征，在数一数、圈一圈的实践过程中更便于操作，不容易出错。

在第二轮教学时，笔者顺应学生的需求，将点子图替换为实物图，摈除非本质因素，突出算理本质。事实证明，在探究后的汇报交流环节中，学生对每一种不同的拆分法的解释都能做到顺理成章，清晰明了，为后续计算方法的掌握与笔算算理的理解起到重要作用。

三、针对前测问题，优化教学设计

在了解学生学情的同时，前测还能真实地暴露学生存在的问题，而学生的问题正是课堂教学要突破的关键点。从前测内容（1）的结果中不难发现，很大一部分学生采用“十位乘十位，个位乘个位，再把两次相乘的积相加”的方法进行计算（如图4 中的方法五）。究其原因，是整数加减的笔算方法带来的负迁移，学生只记得“相同数位相运算”而忽略了乘法的意义。

图4

图5

因此，理解算理、打破负迁移成了本课教学的重点。在第二轮设计中，笔者对教学方案进行再优化：在学生列出算式后，增加了追问“为什么用乘法计算”，唤醒乘法意义的回顾。将原设计方案中直接出示12 套书改为一套一套依次出现，并引导学生边数边说，旨在加深“几个几”的印象。在练习拓展环节，抛出“判断22×13=20×10+2×3 是否正确”的问题，引发讨论，并在此引入点子图，让学生把四次相乘的结果在图上圈一圈、连一连（如图5），很直观地发现，原来“十位乘十位、个位乘个位”的方法只是计算了四次相乘中的两次，计算并不完整。像这样在层层追问、数形结合中，学生对算理的理解不断加深，课堂教学过程愈加优化。

总之，基于对前测结果的分析，能帮助教师合理地选择教学素材、完善教学策略、优化教学设计。没有前测的教学，预设只是一种臆想，课堂抓不住关键，效果可能事倍功半。如果教师在平时的教学中能注重课前对教学对象进行测试与调查，走近学生、了解学生，利用前测结果调整教学方向与思路，那么课堂必将更具实效。