基于改进多目标布谷鸟算法的水资源配置研究

陆 晓，吴 云，杨 侃，汤梓杰

(1.河海大学水文水资源学院，南京 210098；2.山西水利职业技术学院，山西 运城044004)

随着社会经济的发展以及人口的增长，人们对水资源的需求愈来愈大，区域水资源紧缺问题日益突出。在不能完全满足区域用水的条件下，考虑水库调度并对有限水资源进行合理优化配置就显得尤为重要。近年来，启发式智能算法逐渐被用于优化调度中，如遗传算法(GA)[1]、粒子群算法(PSO)[2]、差分进化算法(DE)[3]和蚁群算法(ACO)[4]等，都取得了较好的效果。

布谷鸟算法(Cuckoo Search，CS)[5]是剑桥大学学者Yang Xinshe近年来提出的一种新的智能优化算法，得益于其参数少、操作简单和鲁棒性强，已被成功用于诸多领域。随后，Yang通过引入支配关系和非支配集的概念，构建了多目标布谷鸟算法(Multi-objective Cuckoo Search，MOCS)[6]，将算法拓展到多目标领域。2014年，宋玉坚等[7]引入了非均匀变异算子和差分进化算子对多目标布谷鸟算法进行改进，并用于资源均衡优化问题；2015年，贺兴时等[8]对传统的基于Pareto支配关系的适应度函数进行了改进，并提出了基于小生境技术的逐步档案缩减法，保证了解的均匀性；2017年，马艺元等[9]针对标准算法迭代后期寻优速度慢、易陷入局部解等缺点，提出了结合混沌理论和云模型的多目标布谷鸟算法，通过函数仿真结果证明了该算法的优越性；2018年，张鑫帅等[10]改进了布谷鸟的局部随机游走策略及自适应发现概率，并增加了档案管理机制，之后将其应用于翼型的多目标气动优化设计中，得到了很好的效果；2019年，杨欢红等[11]通过设置动态发现概率和步长，将改进的多目标布谷鸟算法用于微电网调度，克服了原算法的“早熟”现象。目前，虽然多目标布谷鸟算法逐渐受到广泛关注，但仍处于起步阶段，在水库调度与水资源配置方面的应用较少，对于如何实现区域水资源的多目标优化问题，布谷鸟算法将是一种新的求解思路。

本文针对布谷鸟算法容易陷入局部最优解、收敛速度不理想等缺陷，从混沌种群初始化、自适应发现概率和步长及外部档案集维护等方面对MOCS进行改进，并将改进后的算法(IMOCS)应用于山西省同朔供水区的水资源优化配置中，为该区域提供了可行可靠的配置方案，并为解决此类优化调度问题提供了行之有效的新途径。

1 水资源优化配置模型

为了实现区域水资源的高效利用以及促进地区生态文明，本文从供水和生态两个目标入手建立数学模型。

1.1 目标函数

(1)供水单元缺水量最小。

(1)

(2)控制断面河道最小生态流量总缺水量最小。

(2)

式中：Dit,1为规划水平年第i区间第t时段的需水量；Sit,1为规划水平年第i区间第t时段的实际供水量；Dit,2为规划水平年第i区间第t时段的河道内生态需水量，可采用最枯月平均流量法计算得到；Sit,2为规划水平年第i区间第t时段的实际河道内生态用水量；i=1,2,…,N，t=1,2,…,T，N为水库个数，T为供水时段数。

1.2 约束条件

(1)水量平衡约束：

Vwt=Vw,t-1+(Iwt-qwt) Δt

(3)

(2)水库水位约束：

Zwt,min≤Zwt≤Zwt,max

(4)

(3)水库下泄能力约束：

qwt,min≤qwt≤qwt,max

(5)

(4)水库蓄水量约束：

Vwt,min≤Vwt≤Vwt,max

(6)

(5)变量非负约束：所有变量均为非负量。

式中：Vw,t-1、Vwt为第w水库t时段初、末的库容；Iwt为第w水库第t时段的入库流量；qwt为w水库第t时段的下泄流量；Zwt,min、Zwt,max为w水库t时段允许的最小、最大水位；qwt,min、qwt,max为w水库t时段最小、最大下泄流量；Vwt,min、Vwt,max为w水库t时段的最小、最大蓄水量。

2 改进的多目标布谷鸟算法

2.1 标准多目标布谷鸟算法

布谷鸟搜索算法(Cuckoo Search, CS)是通过模拟布谷鸟产蛋行为生成的一种新型智能算法，其搜索机制基于莱维飞行。后来，针对k维多目标优化问题，Yang等又在CS算法基础上提出了MOCS算法，将布谷鸟算法推广至多目标领域。在MOCS中，Yang重新修改了CS中的三条准则[6]，使其满足k个目标的需求：①每只布谷鸟一次产k个蛋，并将这k个蛋随机放入一个鸟巢，第k个蛋代表着第k个目标；②拥有高质量的蛋的鸟巢会保留至下一代；③每个鸟巢中的蛋都有pa的概率被丢弃，并根据蛋之间的相似性重新生成一个鸟巢。

该算法中，第一条准则意味着随机化的过程，新解可以通过莱维飞行或随机游走产生；第二条准则意味着精英策略，有助于算法收敛；第三条准则意味着变异过程，差解被丢弃并生成新解。这三条准则保证了算法的有效性，使之能向最优解收敛。

在此基础上，基于莱维飞行的鸟巢位置更新公式如下：

(7)

其中，u和v服从正态分布。

(8)

式中：Γ为标准的Gamma函数；β一般取1.5。

此外，MOCS的另一种更新方式是根据发现概率Pa与随机生成的数r之间大小来决定是否生成新解，其更新公式如下：

xi,t+1=xi,t+γH(Pa-r)⊕[xj,t-xk,t]

(9)

式中：γ和r二者均服从均匀分布，γ,r∈U[0,1]；xi,t、xj,t、xk,t分别为第t代中3个不同的随机个体；H为赫威赛德函数。

标准MOCS算法的伪代码可参考文献[6]。

2.2 改进的多目标布谷鸟算法

在MOCS基础上，本文针对算法搜索性能、收敛速度及求解效率对原算法进行了以下3方面的改进：通过对种群进行混沌初始化，保证了初始种群的多样性和均匀性，为全局搜索奠定了良好的基础；根据外部档案集的更新情况，动态调整发现概率pa和步长α，有助于算法跳出局部最优解；利用3-点最短路径法对外部档案集进行实时更新和精简，有效提高算法的运行效率，保证最优解的输出。

2.2.1 混沌初始化

MOCS中，初始种群的生成采用随机方式，这有可能导致种群分布不均，也有可能产生大量劣解，导致算法收敛过慢，影响算法性能。混沌是由确定性方程得到的具有随机性的运动状态，是一种非线性现象，具有随机性、遍历性、规律性、对初始条件的敏感性等优点[12]。融入混沌原理的特点，能够有效提高种群多样性，又不失个体随机性，为进一步进行有效全局搜索提供基础。

本文采用Logistic映射对种群进行混沌初始化，其表达式为：

(10)

式中：μ为控制变量，当μ=4时，Logistic映射完全处于混沌状态，本文利用混沌迭代生成布谷鸟的初始鸟窝位置，然后再进行优化搜索，步骤如下：

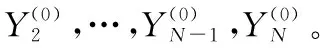
step3：将产生的N个混沌变量按下式映射到解的搜索空间：

(11)

式中：Ud和Ld分别为搜索空间第d维的上下限；yid为利用式(11)产生的第i个鸟巢在搜索空间第d维；xid即为第i个鸟巢在搜索空间第d维的坐标。

2.2.2 自适应发现概率和步长

MOCS中，发现概率和步长是一个非常重要的参数，一般被设为固定值，但这不利于提高局部搜索精度。国内外不少学者，如杨欢红[11]、毕晓君[13]等都将发现概率和步长改为动态的，一般都是将发现概率调整为线性的，步长调整为连续的指数函数，即随着迭代次数的增加，发现概率和步长是不断减小的，这虽然提高了算法的收敛速度，但没有考虑到所有情况。当外部归档集没有更新时，即意味着算法没有搜寻到更优秀的解，此时若继续减小概率和步长，很容易导致算法陷入局部最优解，不利于其跳出局部搜索。因此本文分情况考虑对发现概率和步长进行改进。

在迭代初期，本文将参数pa和α设为较大的值，保证解向量的多样性；若第m代的外部档案集Archive(m)没有更新，则依旧采用第m-1代的发现概率和步长；若有更新，则意味着算法搜寻到了更优解，此时适当减小pa和α，帮助算法局部寻优，提高搜索精度；当迭代到一定次数，pa或α达到最小值时，保持最小值不变继续迭代，以防止发现概率和步长过小导致算法陷入局部最优。

(12)

(13)

2.2.3 外部档案集的生成与维护

MOCS中，Yang引入了支配解与非支配解的概念，比较新解与旧解，保留支配关系最好的一组解，并将非支配存入外部档案集中。但外部档案集存在一定的容量，当Pareto最优解超过其最大容量限制时需要对其进行裁剪，因此需要有合理的档案删除和保留机制。本文参考文献[14]中的方法，利用3-点最短路径法保证非支配解的均匀性和多样性。规则如下：

选定第i个点，设为i1，寻找出与其距离最近的点，设为i2，计算出它们之间的距离为Di1,i2；继续寻找出距i2最近的点，设为i3，计算出i2、i3之间的距离为Di2,i3。此时i1点的3-点最短路径值为：

Di1=Di1,i2+Di2,i3-|Di1,i2-Di2,i3|

(14)

(i1≠i2≠i3)

从公式可以看出，被评估的解点获得的距离值越大则证明其越稀疏，并且分布均匀的解点获得的距离值要大于分布不均的解点的距离值，按照距离值排序可有效维护外部档案集。

2.2.4 IMOCS计算流程

具体流程如图1所示。

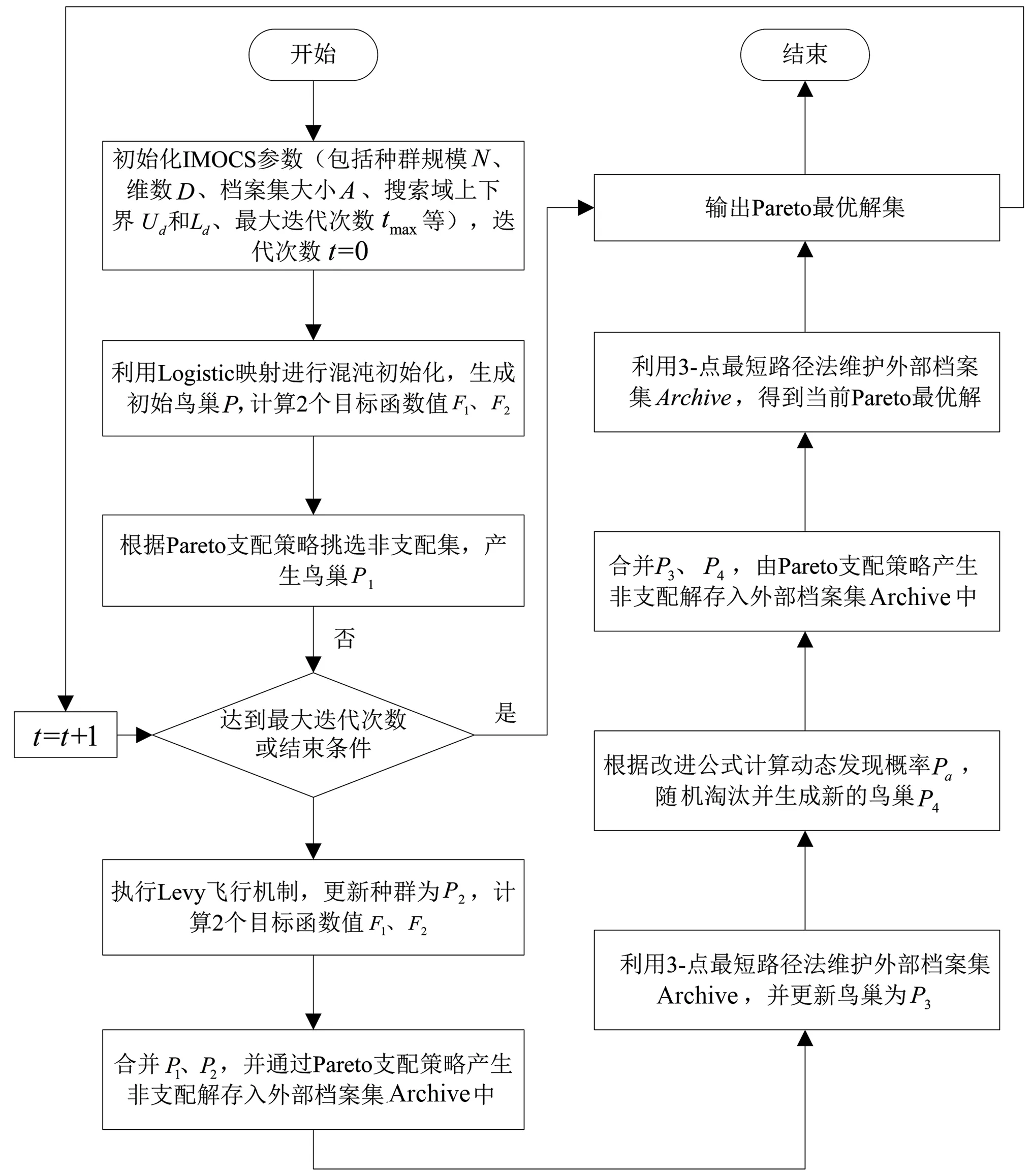
图1 IMOCS算法流程图Fig.1 The flow diagram of IMOCS algorithm

3 实例研究

同朔供水区属于“山西大水网”建设的第一横，位于山西省北部，该区域本身水量不足，再加上随着经济的发展，水资源紧缺的问题日益严重，合理高效配置水资源迫在眉睫。同朔供水区主要涉及12个区县，经简化合并后形成7个供水片区；供水区内的主要河流为桑干河，属于海河流域永定河水系，区域内可供调度的水库为东榆林水库、孤山水库和文瀛湖水库，其中东榆林水库位于桑干河上游，属于中型水库，孤山水库和文瀛湖水库位于御河，孤山水库属于小(Ⅰ)型水库，文瀛湖水库属于中型水库，这3个水库进行联合调度。供水区域及供水路线如图2所示。

依据2018年同朔盆地供水区的需水、当地供水、水库入流及引调水情况，以2018年为现状年，对2025年进行规划，在考虑引调水和不考虑引调水两种情境下，分别对保证率为50%、75%和95% 3种不同情况应用改进的多目标布谷鸟算法求解水库群供水优化调度模型。采用Matlab编写，应用文献[15]中的多目标决策方法，得出各情境下最优调度方案，水库调度过程如图3所示，配置结果如表1、表2和表3所示。

由调度结果可知，平水年时天然来水较多，能够满足部分农业用水，此时整体需水量较小。而在枯水年和特枯水年的农业用水需求更大，总需水量增加明显。平水年、枯水年和特枯水年时供水区都出现了不同程度供水不足的现象，且存在不同程度的河道生态缺水。当考虑万家寨引黄工程后，供水区可供水量增加，缺水现象得到缓解，能够基本满足供水和生态要求。万家寨引黄工程在促进供水区经济发展以及保护其生态环境方面具有重要意义。

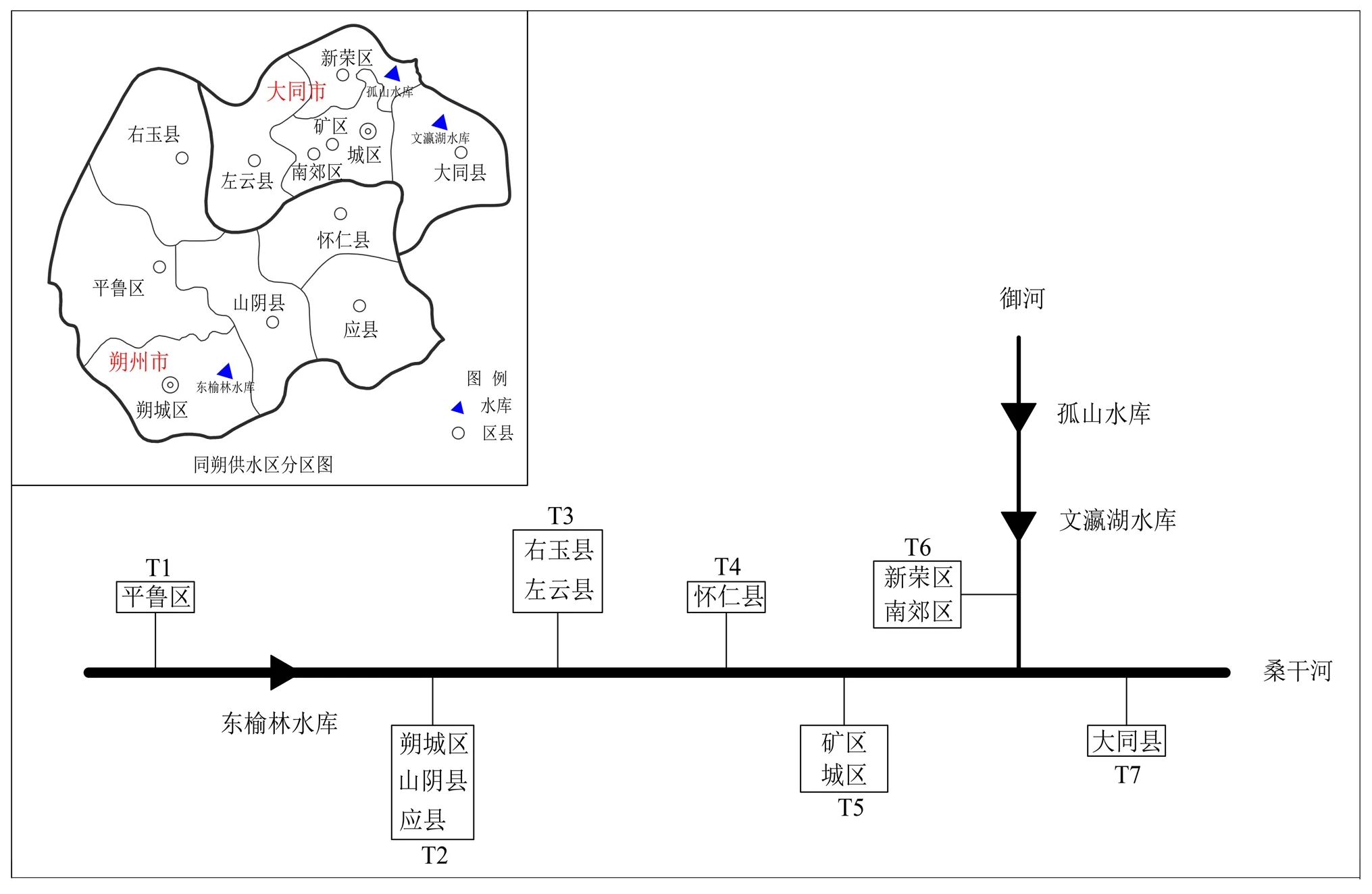
图2 同朔供水区分区及供水路线示意图Fig.2 Schematic diagram of water resource system in Tongshuo water supply area

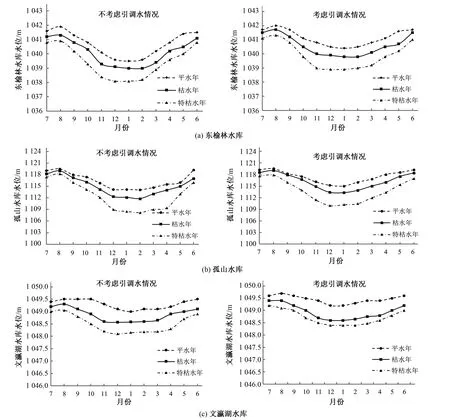
图3 不同情况下2025年各水库调度过程线Fig.3 Water level of reservoirs in 2025 under different scenarios

4 结 语

针对传统多目标布谷鸟算法，本文用混沌映射进行种群初始化、改进自适应步长和发现概率和通过3-点最短路径法进行档案集的删除和保留，从而构建IMOCS方法。对于考虑供水和生态目标的水资源配置问题，以同朔供水区为例，用IMOCS方法进行求解。调度结果验证了该算法的合理性，同时表明万家寨引黄工程对改善供水区的水资源问题具有重要意义。

表1 同朔供水区2025年平水情况下年水量调度方案 万m3

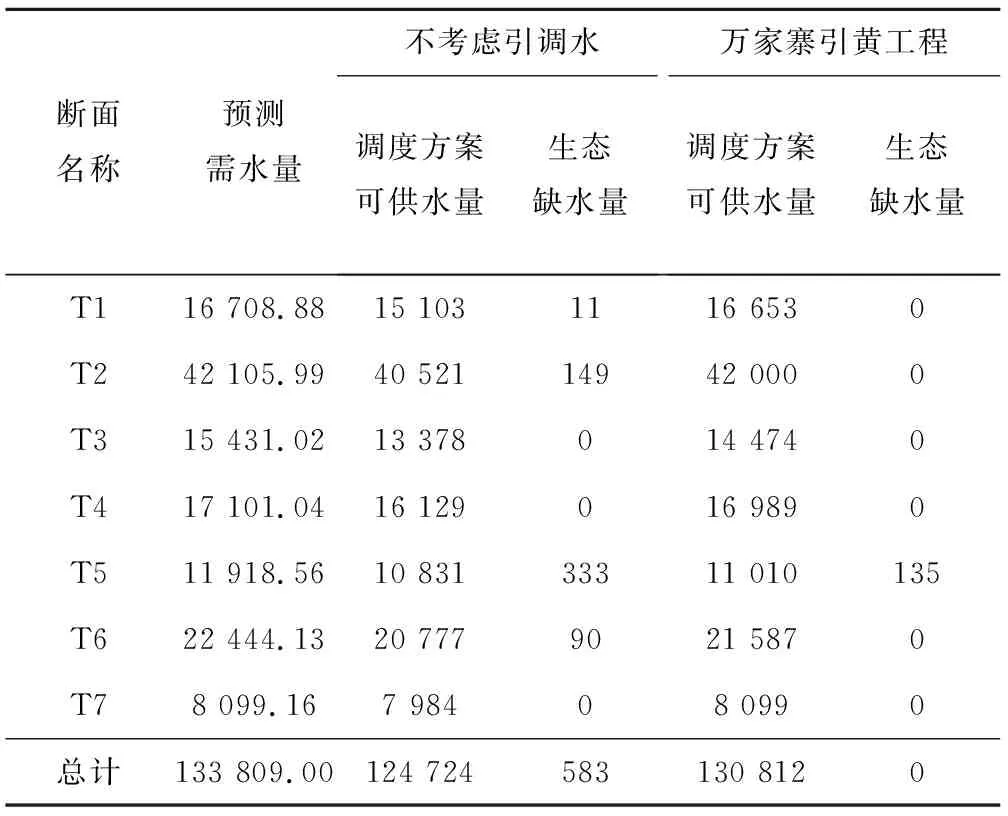
表2 同朔供水区2025年枯水情况下年水量调度方案 万m3

表3 同朔供水区2025年特枯情况下年水量调度方案 万m3

□