孔缝组合式仿生态鱼道流动特性数值模拟研究
2020-06-12胡乔一
胡乔一,祝 龙
(1.南京水利科学研究院水工水力学研究所,南京 210029;2.河海大学水利水电学院,南京 210098)
0 引 言
随着人们对河流资源的不断开发利用,拦河闸坝等水利工程的建设为人们带来便利的同时,也改变了河道原有的自然水文环境,阻断了鱼类自由迁徙的洄游通道,造成生境的破碎化和鱼类栖息环境的变化。鱼道的建设是为了恢复鱼类洄游通道,沟通坝址上下游的鱼类遗传交流,减缓因水文条件改变和闸坝阻隔对水生生态和鱼类的不利影响,承担着保障流域水生态环境的重任[1,2]。
目前,鱼道主要可分为工程鱼道和仿生态鱼道两大类。其中,以竖缝式鱼道为代表的工程鱼道[3-6]研究较为成熟,因其结构规则、水流流态良好、可适应不同的水位变幅、便于施工等特点而被广泛应用。而随着人们对生态环境整体性认识的逐渐深入,意识到鱼道的过鱼效率不仅取决于鱼道进出口与鱼道内的水流流态与水力学指标,更主要的是取决于过鱼对象与鱼道水流之间的协调性。基于这种考虑,仿生态鱼道[7-10]秉承了传统鱼道的基本型式,拓宽了原有鱼道的基本概念,对鱼道建筑材料,结构形式进行生态优化,旨在尽可能满足天然河流的条件,满足不同鱼类的洄游要求。仿生态鱼道断面型式多变,其结构和流态更富多样化,因此比传统的工程鱼道更能满足生物多样性要求,近年来越来越受到业界的关注。对于仿生态鱼道的水力特性和结构设计,国内外研究者考虑了块体障碍物[11-13]、交错蛮石墙[14,15]、透水卵石墙[16]和植物模块[17]等对鱼道水力特性的影响。本文结合以上既有研究成果和某工程实际特点和过鱼要求,就孔缝组合的交错石墙式仿生态鱼道进行三维数值模拟研究,分析底孔、边坡和底宽等结构变化对鱼道水力特性的影响,为仿生态鱼道的结构和理论提供参考。
1 数学模型建立及验证
1.1 基本方程
流体运动遵循质量守恒原理和牛顿第二定律,则计算需满足连续性方程和动量守恒方程。本文流场模拟采用FLOW-3D软件,在建模时采用“FAVOR”技术,即在模型中加入含有面积和体积分数的参数,在直角坐标系下表示为:
连续性方程:
(1)
动量守恒方程:
(2)
(3)
(4)
式中:ρ为流体密度,kg/m3;p为作用在流体微元上的压强,Pa;u、v、w为x、y、z方向上的流速分量,m/s;Ax、Ay、Az表示3个方向上可流动的面积分数;Vf为可流动的体积分数;Gx、Gy、Gz为3个方向上的重力加速度,m/s2;fx、fy、fz为3个方向上的黏滞力加速度,m/s2。
为模拟鱼道复杂的紊动水流结构,本文采用RNGk-ε紊流模型对Navier-Stokes控制方程组进行封闭,同样在模型中加入含有面积和体积分数的参数,则紊动能kT和紊动耗散率εT的输运方程表示为:
紊动能方程:
(5)
紊动耗散率方程:
(6)
式中:PT为由速度梯度引起的紊动能产生项;DT和Dε为紊动扩散项,其表达式为:
(7)
(8)
(9)
式中:vk和vε为紊动扩散系数,由运动黏滞系数vT而定,其中vT可表示为:
(10)
同时,计算过程中对εT进行严格控制,避免造成不符合实际的巨大紊动能耗散。
采用tru-VOF方法捕捉自由水面,流体体积函数F用以表示计算域中每个单元所占的体积与该单元可容纳的流体体积之比,F=1表示充满水体,F=0表示充满气体。通过求解F的输运方程,进行自由水面的追踪,体积分数F的输运方程为:
(11)
1.2 计算区域及网格划分
基于某实际工程,枢纽区段河道内基本没有巨石、漂石存在,鱼道不宜采用大体积漂石布置,在传统异侧竖缝式鱼道的特点上进行生态优化,采用梯形断面,隔墙采用厚60 cm的石笼隔墙,即能尽可能保持鱼道内部构造与自然河流相类似,又便于施工建设。鱼道过鱼对象以四大家鱼等经济鱼类为主,根据鱼类的游泳能力,控制鱼道池室控制断面最大流速在1.0 m/s左右。建立鱼道概化数学模型,鱼道池室结构及隔墙布置型式如图1所示,单鱼道池室长7.0 m,底宽3.0 m,底坡1∶150,边坡1∶2,隔墙交错布置,按不透水建模,在长隔墙下部开有40 cm高的孔洞,便于底层鱼类钻孔上溯,同时亦可改善池室内水流条件。
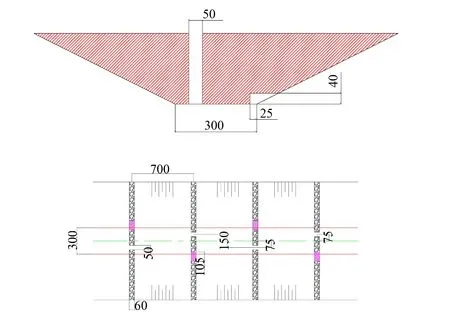
图1 鱼道模型示意图(单位:cm)Fig.1 Schematic of fishway model
为了全面了解该种体型鱼道池室的水流条件,便于在鱼道布置过程中根据实际地形地质条件对鱼道断面型式进行调整,针对上述鱼道结构,分别改变了边坡和底宽,封堵贴坡底孔,列出了5种计算工况,如表1所示。
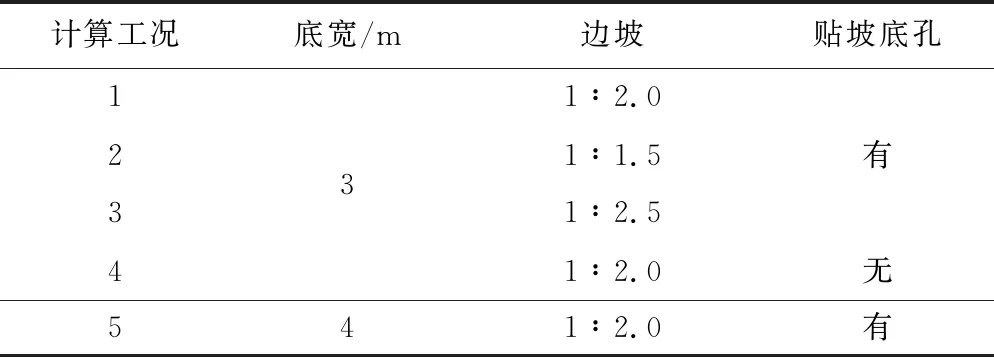
表1 仿生态鱼道结构变化不同工况参数Tab.1 Natural-like fishway parameters of different projects
为减少进出口边界对池室流场的影响,数值模拟了8道隔墙,7个池室,以及上下游平段,平段取池室长度的2倍。采用六面体结构化网格对模型进行网格划分。考虑模型运算效率和求解精度,选取网格尺度0.1、0.08和0.06 m分别进行模拟,经测试,0.08 m网格尺度下竖缝处最大流速变化已经不大,可用于研究分析。
1.3 定解条件和计算方法
数学模型进出口均采用压力边界条件,设置鱼道进出口原型水深为1.0 m,顶部为大气压力边界条件,同时设置流体体积分数为0,表明全为空气,鱼道隔墙和底部设为固壁边界,其表面粗糙,模型设置粗糙高度为0.01 m。模型设置初始水位,以静水压力初始化,使模型收敛更快。模型选用GMRES隐式算法进行计算,其计算精度高,收敛快且不易发散,计算采用自适应步长,初始步长设置为0.01 s,最小步长为1×10-7s。
1.4 模型验证
鱼道物理模型按照重力相似准则设计,模型比尺为1∶10,模型实测鱼道运行流量0.58 m3/s,本文计算鱼道运行流量为0.59 m3/s,与物理模型试验实测流量基本一致,说明数学模型的结果可信。
对鱼道最重要的竖缝和底孔处流速进行验证,数学模型测得各隔墙竖缝和底孔处平均流速分别为1.01和0.97 m/s,最大流速分别为1.04和1.00 m/s,物理模型测得各隔墙竖缝和底孔处平均流速分别为0.97和0.91 m/s,最大流速为1.03和1.01 m/s。数学模型算得的流速与物理模型基本一致,表明数学模型设置合理。
运用本论文的数学模型模拟文献[18]的模型,以鱼道池室ADV数据对本论文数学模型进行验证,提取10号池室第三横断面上流速数据,断面位置及验证结果如图2所示,其中y为距离鱼道池室边墙的距离,进一步说明数学模型能较好地模拟鱼道水力特性,可用于后续研究。
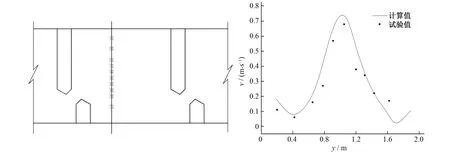
图2 计算值与试验值对比Fig.2 Comparison of simulated and measured velocities
2 结果与分析
2.1 池室流态分析
仿生态鱼道由于采用梯形断面,其水流具有明显的三维特性,研究自鱼道池室底部向上划分0.2h、0.5h、0.8h(h为鱼道水深)3个分析层,代表鱼道底层、中层和表层的水流特性。计算工况1池室底层整体水流流速云图如图3所示,可知鱼道每个池室水流结构相似,仅竖缝和底孔在鱼道内的相对位置不同,造成鱼道主流的位置不同,而水力特性相似。为了分析池室中的流速特性,可以中间级池室作为代表池室进行分析。
鱼道池室缩窄断面的流速和池室的流态是影响鱼道过鱼效果的重要因素,要求鱼道竖缝和底孔内水流流速小于过鱼对象的极限流速,这样鱼类才能顺利完成洄游。同时鱼道池室内要求主流明确,因消能要求允许有一定的回流,但回流又不能过于剧烈,范围不能过大,以免一些小型鱼类迷失方向,影响过鱼效率[10,19,20]。为了对比增设贴坡底孔对鱼道池室水流条件的影响,图4列出了工况1和4不同水层的流态对比图。

图3 池室底层整体水流流速分布图Fig.3 Distributions of flow velocity in bottom layer
已有工程[10]研究表明,仿生态鱼道隔墙透水率应小于0.25;过水(鱼)槽偏移率介于0.3~0.6之间较为合适;池室长度小于8 m较为合适。本论文鱼道尺寸亦在上述范围以内,鱼道竖缝和底孔处的流速均在1.0 m/s左右,其主流明确,大致位于池室中央,两侧均有回流区存在,主流总体弯曲程度不大,有利于过鱼,表明鱼道透水率和偏移率设置合适,整体水流流态良好,满足消能要求。当不设置底孔时,鱼道运行流量0.40 m3/s,下泄水流只有竖缝处一股水流,竖缝交错布置,主流蜿蜒前进,从上一级竖缝流向下一级竖缝,在池室内绕行,两侧回流范围大小相当。鱼道为尽可能模拟天然河道条件,采用梯形断面,不同水层流场结构相似,底层断面宽度最小,但在主流两侧仍存在两个可供鱼类休息的小流速回流区,越往上层,宽度越大,水流能量耗散充分,小流速范围也越来越大,但整体流态比较单一。当鱼道设计了贴坡底孔,隔墙处的透水率增大,鱼道整体运行流量较不设底孔时增大,运行流量为0.58 m3/s,但差距不大,竖缝和底孔处的流速也满足设计要求。鱼道下泄水流分为垂直竖缝和贴坡底孔两股,水流流态更具多样化,主流两侧回流区发生变化,没有底孔一侧仍有较大的回流范围,但范围大小较不设底孔时略有减小,设置底孔一侧流态复杂,存在局部较小的回流漩涡。鱼道各个水层水流主流依旧明确,各水层流场结构存在差异,底层隔墙孔缝最大流速较中上层要略大,整体较好地营造出了“大流速区”和“小流速区”,更利于不同种类、不同水层的目标鱼类上溯,特别是设置贴坡底孔为中底层鱼类增加了上溯路径。对比工况1、2、3、5的计算结果,各个计算工况下鱼道池室内流场结构基本相似,在此不再赘述。
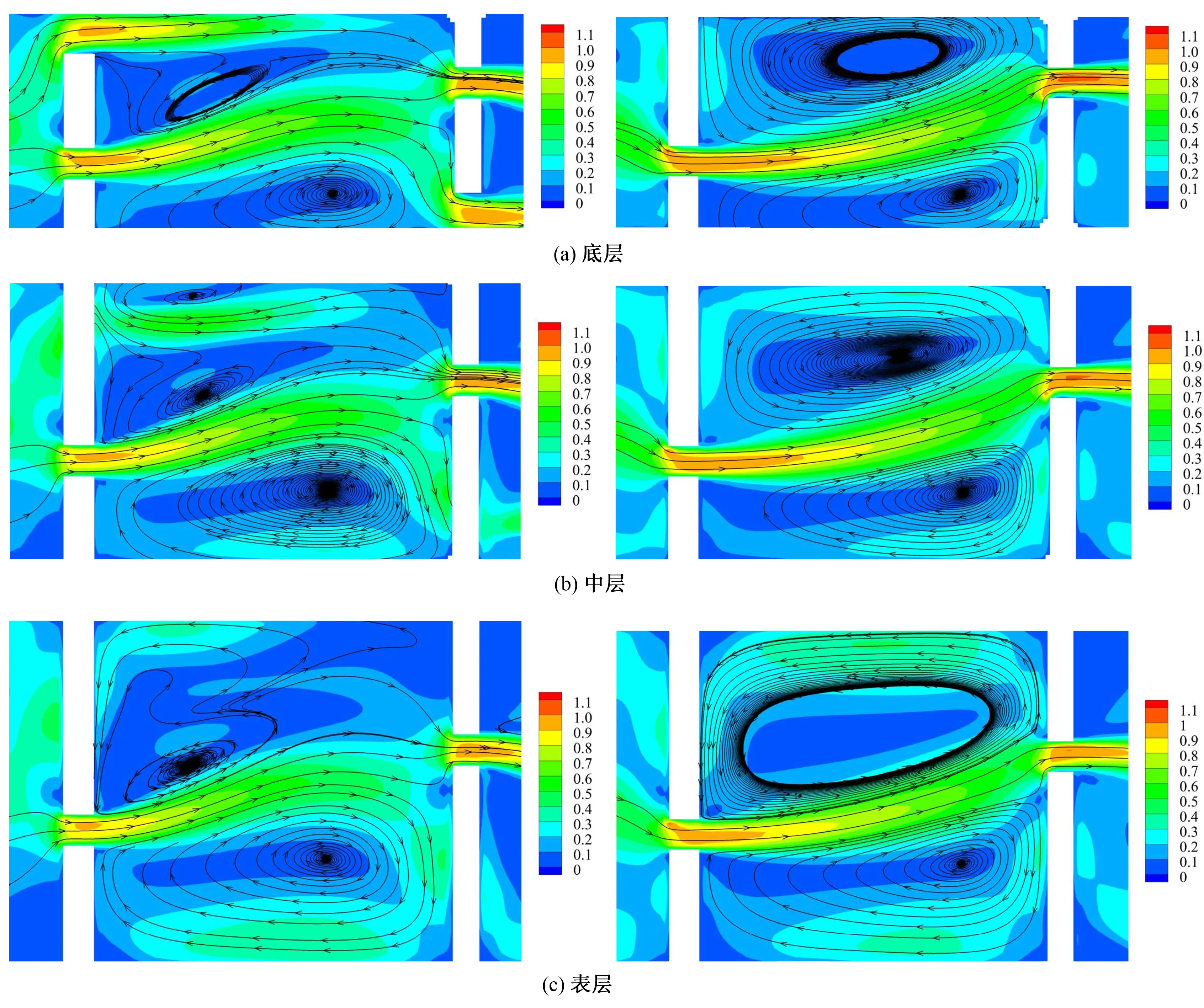
图4 有无底孔鱼道池室不同水层流态对比(单位:m/s)Fig.4 Comparison of flow patterns with or without orifice
2.2 主流流速衰减规律分析
为了探究结构变化对鱼道控制断面和鱼道池室流速的影响,研究统计了各隔墙竖缝和底孔处的最大流速,取其最大值和平均值,将各工况统计数据列于表2。以中间池室作为代表池室,分三个分析水层沿鱼道长度方向每隔0.35 m设置一个测流断面,每个水层共21个测流断面,统计每个测流断面上的最大流速,则其流速的沿程变化能够一定程度反映出池室内沿程水头损失,一般认为流速沿程衰减效果越好,鱼道消能特性越好,更有利于过鱼[4,5]。各工况主流流速沿程变化规律如图5所示。
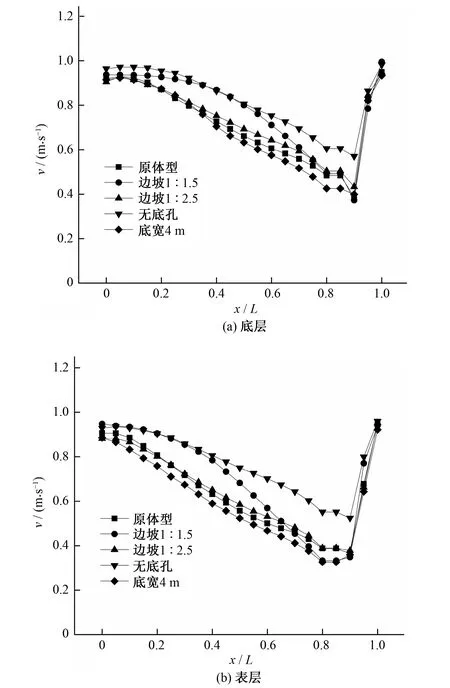
图5 主流流速沿程变化规律Fig.5 Maximum velocity distribution along the pools
从控制断面流速来看,由于边坡放缓和底宽增大,池室面积增大,水流能量耗散相对充分,鱼道控制断面流速略有减小,而边坡变陡则相反,但总体而言各工况数据相差不是特别大,可以表明底宽变化和边坡变化对鱼道控制断面流速影响不大。从主流流速沿程变化来看,不同水层流速衰减规律相似,主流从鱼道隔墙控制断面开始流速逐渐减小,到下一个隔墙附近再增大,水流扩散充分,消能效果良好,但由于表层池室面积最大,水流扩散更为充分,衰减效果略好于中底层。而设置底孔加大了水流的紊动扩散,主流流速衰减效果优于不设置底孔的情况,更有利于过鱼。当边坡1∶1.5时主流流速衰减相对其余工况效果不佳,这是由于池室面积变小,主流扩散程度不够的原因,综合分析得出底宽和边坡变化对鱼道水力特性的影响较小,边坡以不陡于1∶2为宜,实际应用在保证竖缝和底孔相对位置不变的情况下,可根据具体工程地形地质条件作适当调整。
2.3 紊动能分析
在鱼道中,水流紊动耗散,具有一定的紊动能。紊动能过高,鱼类为克服紊流障碍而消耗更多能量,且会降低鱼类的游泳能力和平衡能力,使其无法顺利完成上溯。合适的紊动能为鱼类提供了良好稳定的水流条件,保障鱼类的上溯[21,22]。限于文章篇幅,以中间水层为例,图6给出了计算工况1和计算工况4的紊动能分布,可知计算工况1设置底孔,底孔出流处紊动能较不设置底孔时略大,在0.03 m2/s2左右。总体来说,两种计算工况紊动能不大,主流区紊动能基本在0.04 m2/s2以下,基本不构成鱼类上溯的障碍,有利于鱼类长时间洄游。
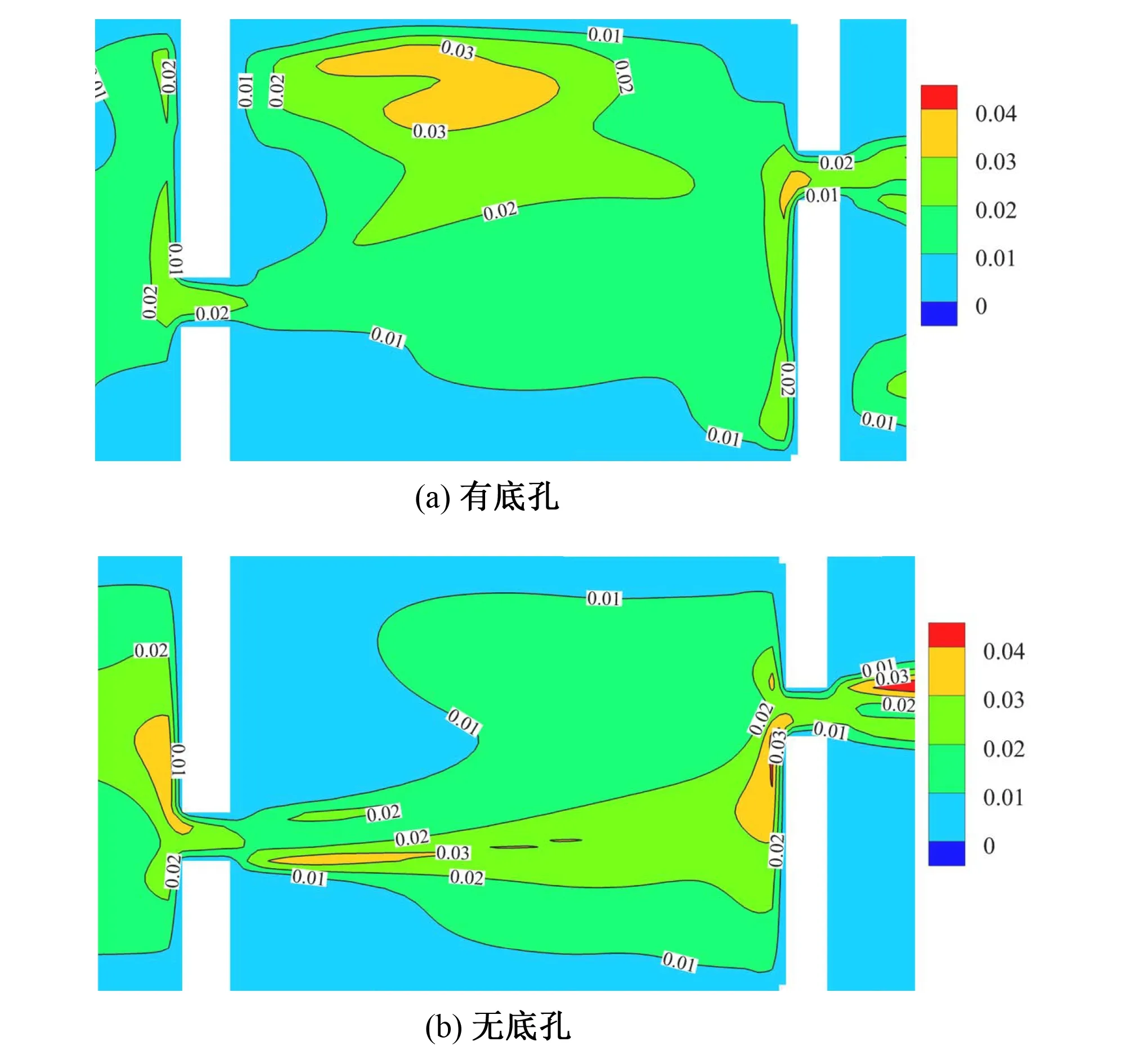
图6 紊动能分布图(单位:m2/s2)Fig.6 Distributions of turbulent kinetic energy
3 结 语
本文基于某工程实际特点,建立孔缝组合型式仿生态鱼道三维数学模型,对增设底孔,底宽边坡等结构变化对池室水流条件的影响进行分析,研究表明:
(1)仿生态鱼道具有明显的三维水力特性,该鱼道隔墙型式合理,主流明确,流速衰减充分,竖缝和底孔处流速为1.0 m/s左右,紊动能整体合理,基本满足“四大家鱼”等经济鱼类上溯条件。
(2)增设底孔可为中底层鱼类上溯增加路径,使得鱼道池室表、中、底三层水流流态存在差异,能够有效提高过鱼效率。
(3)底宽和边坡变化对池室流速指标影响不大,实际应用时可根据地形地质条件作适当调整,可适当增大底宽和放缓边坡以改善池室水流条件。
本文数学模型对仿生态鱼道作了一定概化,实际上,仿生态鱼道采用透水材料筑成,过水断面难以做到整齐划一,且断面型式多变,更有待于进一步研究。
□
