细长圆柱体非均匀磁化研究

张新邦，陈德祥，王东盛，韩杨杨，屈盼玲，张金巍

（北京控制工程研究所，北京 100190）

0 引言

有文献认为均匀铁磁介质构成的细长圆柱体，在均匀外磁场中是均匀磁化。文献[1]在沿轴向均匀磁化的条件下，对圆柱形均匀介质进行退磁场和退磁因子研究。文献[2]的研究中忽略圆柱体内的体磁荷，这等于认为其轴向均匀磁化。也有文献提出只有在二次曲面形状（椭球形）的情况下物体才能均匀磁化，圆柱体内退磁因子只是近似值，并不是严格意义下的解析解。所以文献[3]和[4]提出了圆柱体退磁因子近似值；而文献[5]内圆柱体退磁因子表是采用旋转椭球体计算出来的，计算时圆柱体长度和直径相当于椭球体纵向和横向主轴的长度。

如果圆柱体沿轴向均匀磁化，则磁荷集中于圆柱体两端，体内无体磁荷，符合偶极子标准，外面场强可按偶极子规律进行计算。如果不是均匀磁化，其磁化强度按某曲线形状分布，则不是一个标准的偶极子，尤其近距离情况下外部场强不能按偶极子规律进行计算。文献[6]对舰船单磁偶极子模型适用性进行研究，得出了当距离大于2.5倍舰船物理尺寸处，单磁偶极子有较高的模型拟合度。文献没有深入探讨近距离时模型拟合度低的原因和解决方法。

舰船和细长圆柱体等物体近距离时单偶极子模型拟合度低，原因是轴向的非均匀磁化特性。解决的途径之一是：研究其磁化强度曲线，再根据磁化强度曲线应用由磁矩求场强方法，可以较准确地得到近距离的场强。

应用面磁荷和体磁荷观点以及退磁场理论推导退磁场和磁化强度的公式，根据磁化率的定义得到退磁场和磁化强度的另一个公式，以此建立方程组解方程得到磁化强度曲线，根据曲线计算得到结果和试验结果吻合。

细长体是一类较普遍存在的物体，非均匀磁化特性对其近距离试验十分重要，这方面的研究具有现实意义。

1 技术准备

1.1 磁荷

铁磁体内有许多微小的磁畴，磁畴是磁性材料内部的一个个小区域，每个区域内部包含大量原子。同一磁畴区域内原子的磁矩都整齐排列（称为自发磁化），但磁畴之间磁矩排列的方向混乱，宏观上相互抵消，即物体的磁化强度为0。

以细长圆柱体为研究对象，当圆柱体轴向有了外磁场，体内各磁畴的磁矩在磁场力矩作用下转向磁场方向整齐排列（图1（a）），物体内部磁畴的N、S极（即＋、－极）首尾衔接，相互抵消。若物体是均匀磁化，宏观上物体内部无磁荷，在两端出现＋、－磁荷（图1（b）），称为面磁荷。

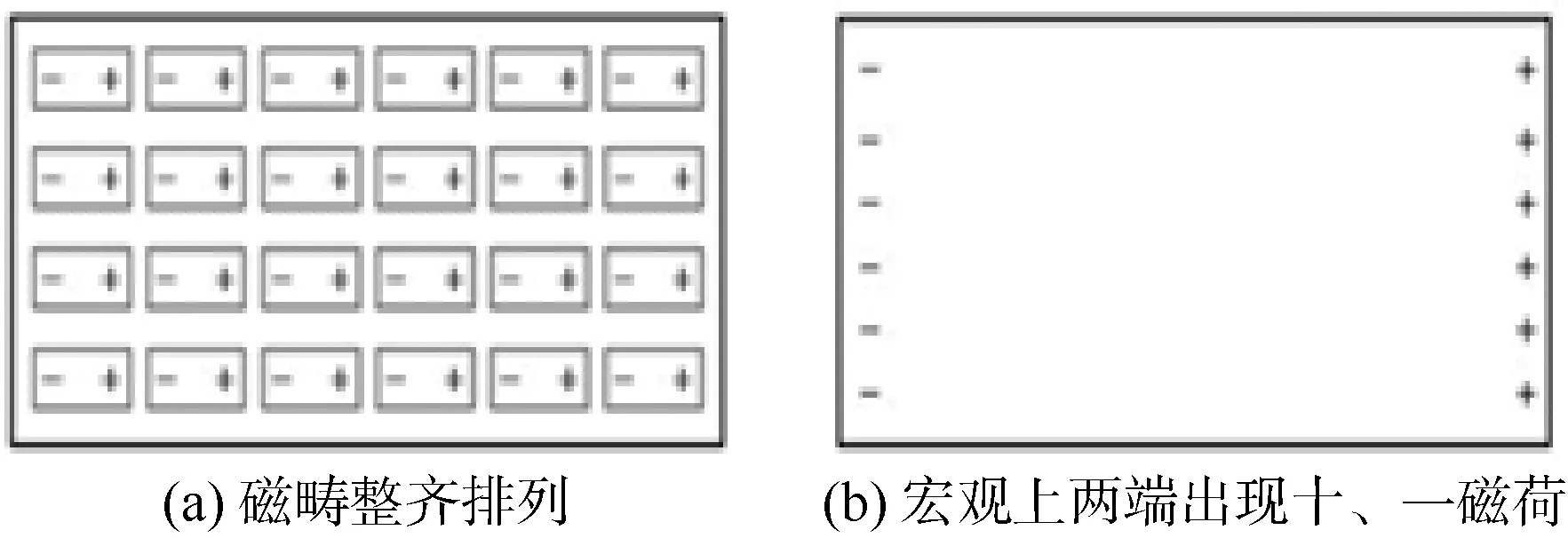
图1 磁畴排列和磁荷的出现Fig. 1 Magnetic domain arrangement and the appearance of megnetic charges

设图1（b）内圆柱端面出现磁荷P，当圆柱直径相对有关的距离是小量，则认为P为点磁荷。如不是小量，且假设磁荷均匀分布，则引入端面的磁荷面密度Q，有：Q=P/S。其中，S是端面的面积。

当圆柱体沿轴向非均匀磁化，则体内产生磁荷。在体内某点取体积元ΔV，体积元内磁荷ΔP，引入磁荷体密度σ，有：σ=ΔP/ΔV。

1.2 磁荷与磁化强度

为了描述磁介质的磁化状态（磁化方向和磁化程度的大小），引入磁化强度M，它定义为单位体积内磁畴磁矩的矢量和。如在磁介质内取体积元ΔV，其中包含了大量的磁畴，用∑md代表这体积元内所有磁畴磁矩的矢量和，用M代表磁化强度，则上述定义可表达成下面公式

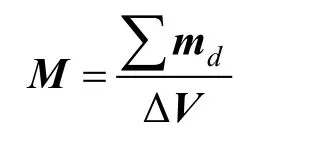
文献[7]给出了磁化强度M与磁荷P之间关系有如下公式

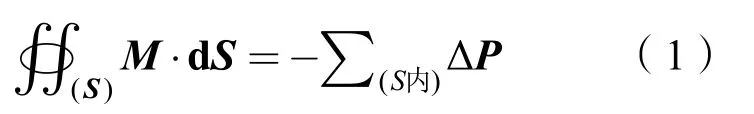
其中S是一个任意的闭合面，等式右边为包含在S内磁荷代数和的负值。

下面进一步分析圆柱体内磁荷密度与磁化强度之间关系。

图2 圆柱体内的试验段Fig.2 Test section in the cylinder

假设垂直于轴的截面上介质是均匀磁化，取圆柱体的某小段为试验段（见图2），段左侧截面S1，磁化强度M1；右侧截面S2，磁化强度M2；试验段体积ΔV；段内的磁荷量ΔP。设截面积为S，以整段的表面积为闭合面运行公式（1），有

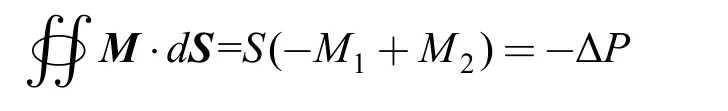
即

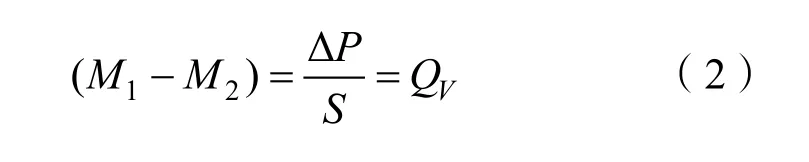
式中，QV是等效面密度，是将试验段两端压缩成平面后得到的面密度，有等效面密度等于试验段两端磁化强度之差。

若试验段包含了磁棒左端面且段的长度极小，则得到左端磁荷面密度

同样对于磁棒右端面得到

此结果也可用下面简单方法证明，偶极子的磁矩为m=LP，其中：L为极间距离；P为磁极强度即磁荷总量。将等式两边除以体积V，即有

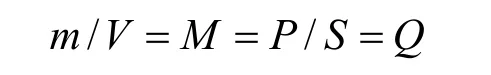
式中，S为端面的面积，于是有Q=M。

设沿轴x方向有磁化强度曲线M（x），有：曲线在圆柱内连续且可导，圆柱两端是曲线的断点，曲线断点处磁荷面密度（绝对值）=磁化强度（绝对值），曲线连续处磁荷体密度=曲线斜率。

1.3 磁荷产生磁场强度

1.3.1 点磁荷

当磁荷P（或称为磁极）为点磁荷，设点磁荷在r处对磁场的贡献为h（r），有

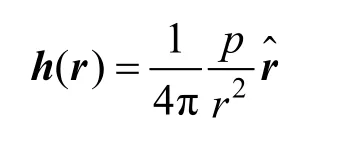
这是点磁荷生成磁场的公式，当r很小时此公式失效，需要提出面磁荷生成磁场公式。

1.3.2 面磁荷和面密度贡献系数

设磁荷P均匀分布在一个半径为R的圆上，圆平面上的磁荷面密度Q，有

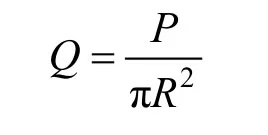
过圆的圆心O点作垂直于圆平面的轴x（见图3），在x轴C点（坐标为x）产生的磁场强度为h，h的方向和x轴相同。

圆上有A点，其极坐标为（r,θ），有

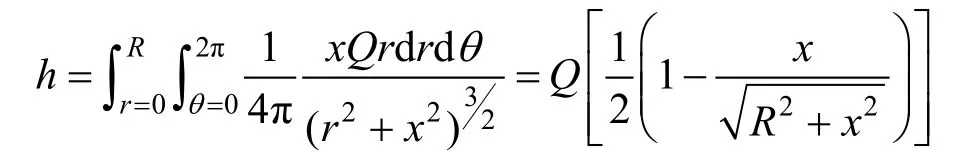
改写为

F（x）也称为面密度贡献系数，于是有：场强=面密度×面贡献系数。

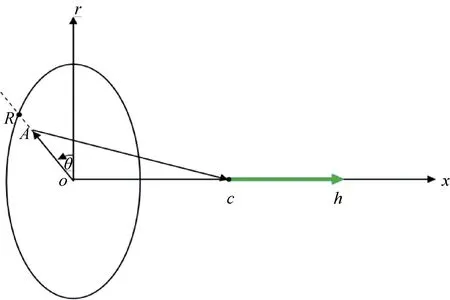
图3 磁荷面密度产生磁场强度示意图Fig. 3 Schematic diagram of magnetic field intensity generated by magnetic charge surface density

1.3.3 体磁荷和体密度贡献系数

以图2内的试验段为例，试验段长度ΔL，试验段内有体磁荷，将试验段均分成N份，每份成为薄片可近似为一个面。应用公式（2）可以得到试验段的等效面密度QV，则各薄片的磁荷面密度为QV/N。设第i份薄片到测点的有向距离为xi，对测点贡献的场强为hi，应用公式（5）得到

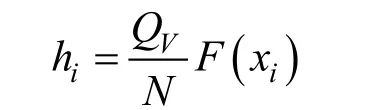
整个试验段对测点贡献的场强为

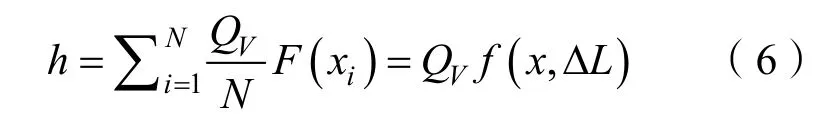
其中

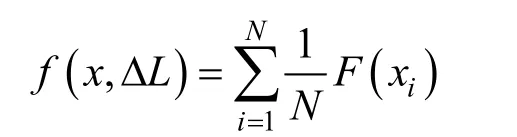
也称为体密度贡献系数，于是有：场强=等效面密度×体贡献系数。

2 建立关于磁化强度方程组

研究圆柱体的不均匀磁化，需要得到磁化强度M沿轴向的变化曲线，方法是建立关于M的方程组，解方程组即可得到磁化强度曲线。

将磁棒均分成N段（图4），各段分别表示为D0～DN-1。均分后得到N+1个界面，表示为A0～AN。

设界面An处磁荷面密度Qn，磁化强度Mn，退磁场h(n)(n=0～N)。第n段（Dn）内体磁荷的等效面密度QVn(n=0～N-1)。

注意磁化强度曲线就是由Mn(n=0～N)数据组成。

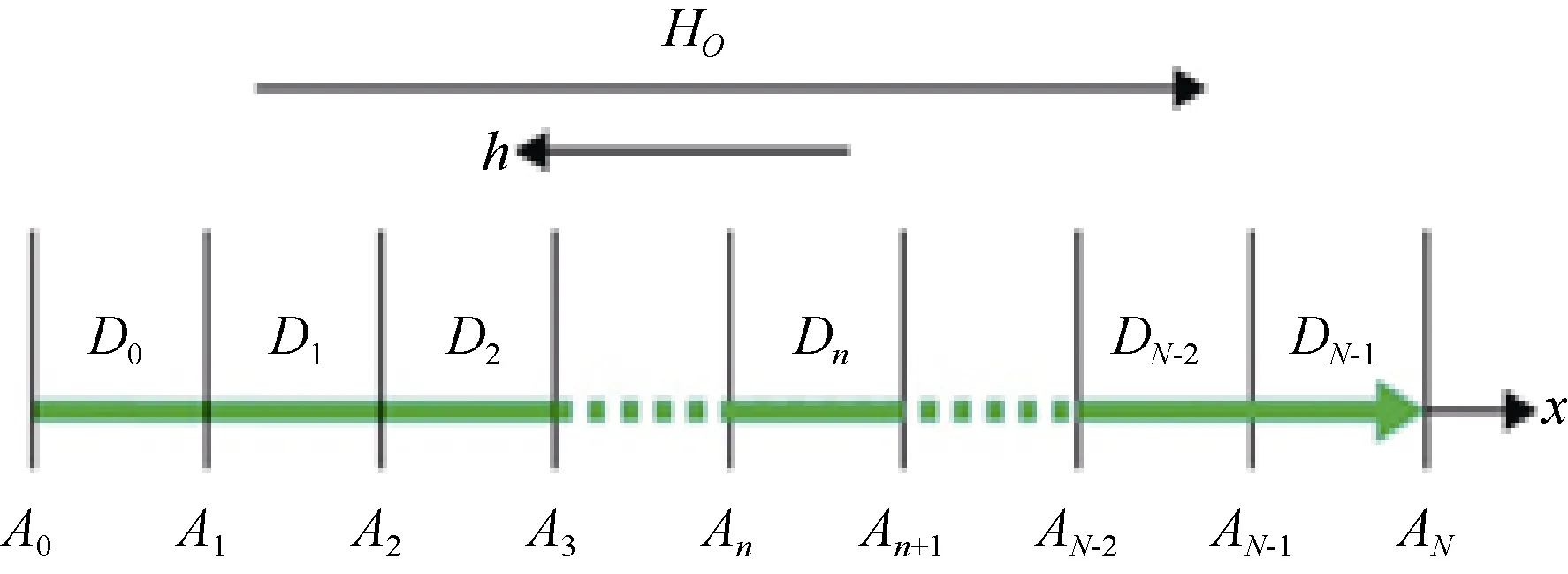
图4 圆柱体分段示意图Fig. 4 Section diagram of the cylinder

图4中：HO是外磁场，h是退磁场。由于外磁场、退磁场和磁化强度等的方向都平行于棒轴，计算中可以只应用其x分量。

应用式（5）-（6）分析面磁荷和体磁荷对退磁场的贡献，设j界面的面密度对i界面退磁场贡献系数为Fij。由于只有A0和AN这2个界面是面磁荷，有：A0面磁荷对Ai退磁场h（i）的贡献为Q0Fi0；AN面磁荷对Ai退磁场h（i）的贡献为NiN QF。设段Dj体磁荷对Ai退磁场(i)h的贡献为hij，贡献系数为f ij，有

于是有

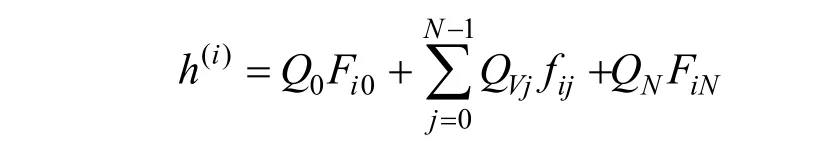
根据公式（2）-（3）有

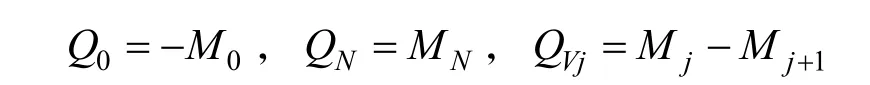
于是

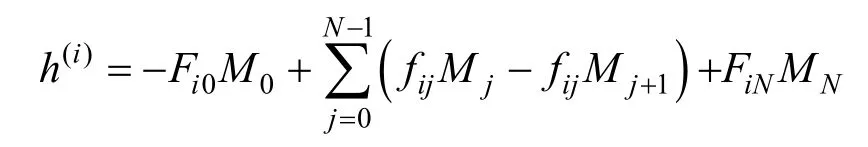
改写为

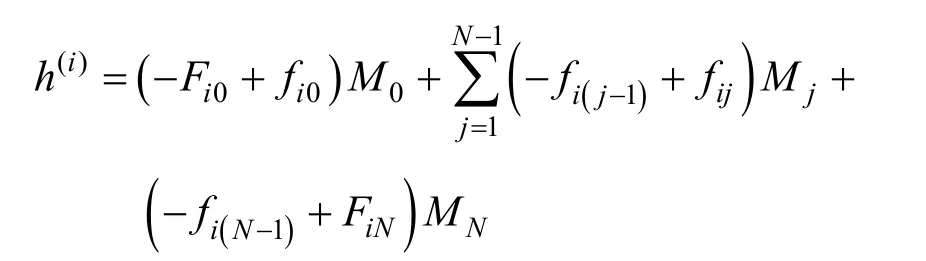
应用新的系数Aij，将上式改写为

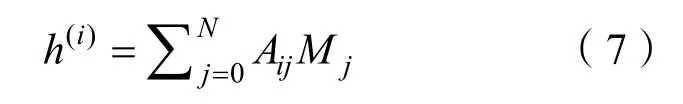
其中

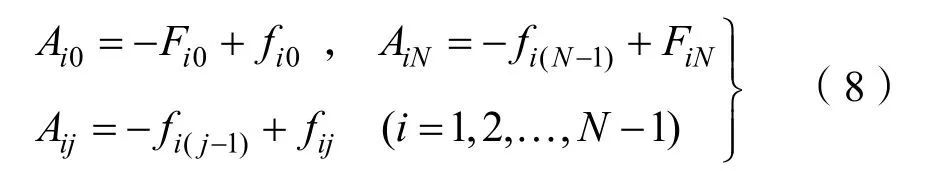
由磁学理论可知磁化率（χ）、磁场强度（H）、磁化强度（M）有如下关系

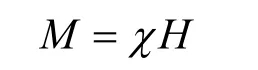
而H=h+HO，其中h是退磁场，HO是外磁场，于是有

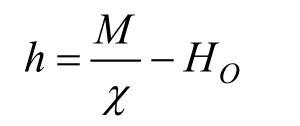
对第i界面处的退磁场(i)h和磁化强度Mi，有

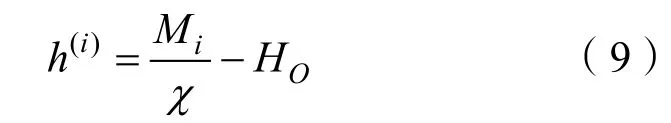
将式（7）与（9）联合并以详细形式表达

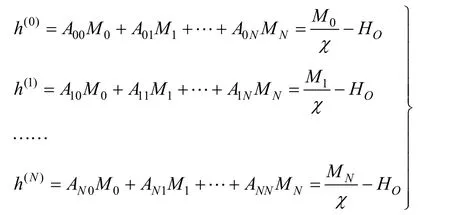
即有

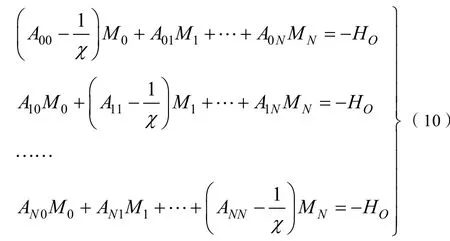
改写为

于是有

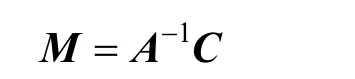
3 细长圆柱体磁化强度曲线

以坡莫合金为介质的圆柱体长L=0.8m，半径R=0.01m ，磁化率χ=10000，外磁场强度HO=300A/m，计算时将圆柱体分80等分，每等分再分成50份薄片，列出方程组并求解得到磁化强度曲线（图5），计算得到圆柱体总磁矩为24 A·m2。

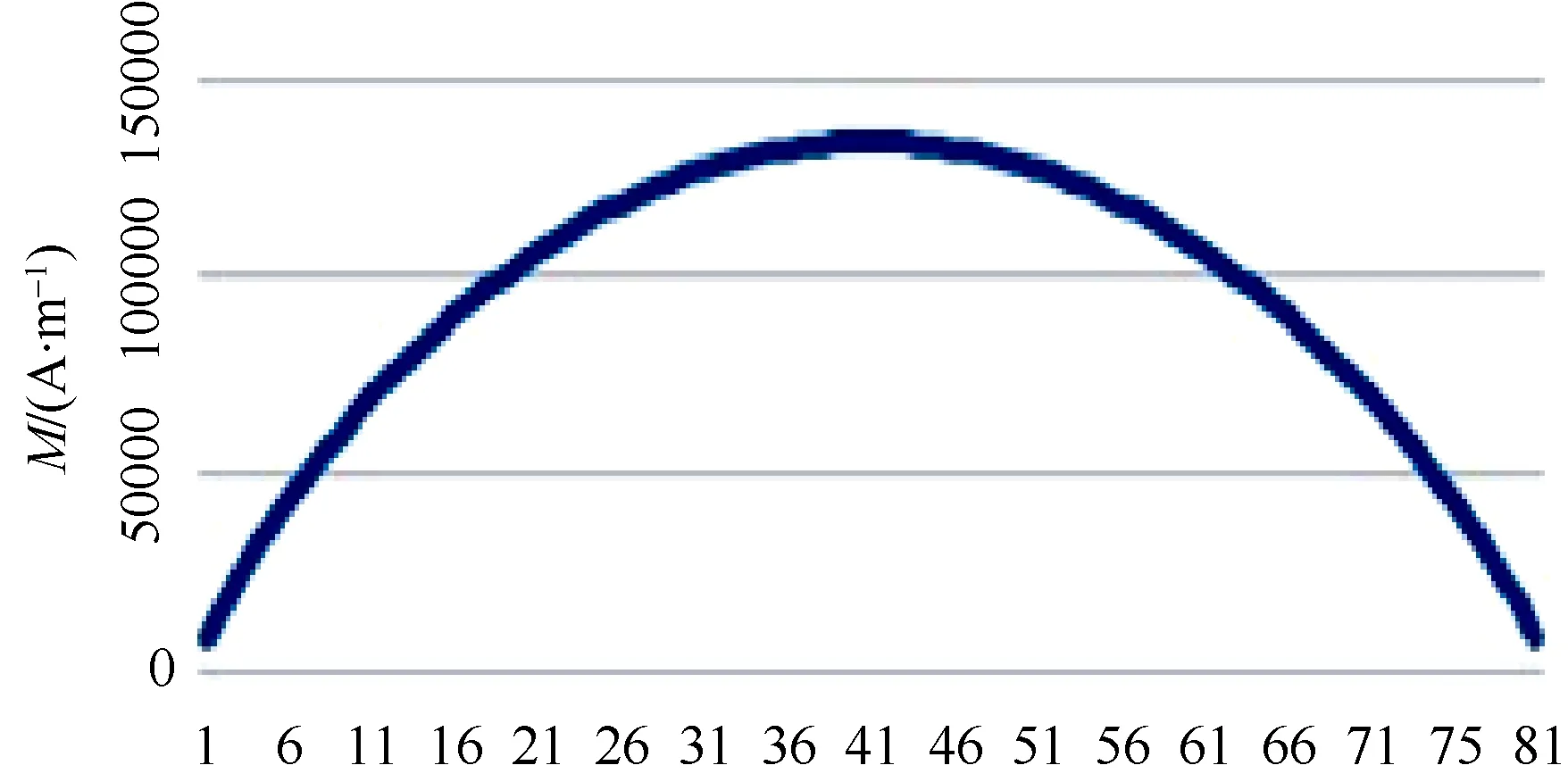
图5 细长圆柱体磁化强度曲线Fig. 5 Magnetization curve of slender cylinder

由磁化强度曲线求外部某点磁场强度，需要应用由磁矩计算磁场强度公式[8]，将圆柱体均分N份，根据曲线得到每份的磁矩，计算每份磁矩产生的场强，再求和得到需要的值。

以圆柱体中心为原点建立坐标系，圆柱轴为x轴并指向磁体正极，为验证近距离的计算结果，取近距离点p坐标为（0.5L，0.25L，0）。由磁化强度曲线计算得到p点磁感应强度x分量为10 000 nT以上，实际测量得到磁感应强度x分量约10 000 nT，两者基本吻合。而用偶极子模型计算得到磁感应强度x分量约-4 000 nT。

4 结束语

1）细长圆柱形均匀介质在均匀外磁场中不是均匀磁化，研究其非均匀磁化特征是有现实意义的。

2）应用磁化强度、面磁荷与体磁荷、退磁场之间关系建立圆柱体磁化强度方程组，解方程得到其磁化强度曲线，由曲线计算得到的近距离场强结果和试验数据吻合。

3）在计算退磁场时既考虑面磁荷也考虑体磁荷，并建立和求解磁化强度方程组最后得到磁化强度曲线，此结果和方法在以前文献中未见报道。