电磁发射深水炸弹空中弹道性能仿真分析
2020-06-12戴文留昌铁强廖欢欢李永锋万小辉
戴文留,昌铁强,廖欢欢,李永锋,杨 剑,万小辉
(中国兵器工业集团有限公司第282厂,湖南 湘潭 411207)
0 引言
电磁发射技术及相关设备的研究是近年来兴起的一个研究热点,是一项正在逐步发展、完善的尖端推进技术[1]。电磁发射技术借助电磁力做功,可以将电磁能转化为弹丸的飞行动能,与传统的化学推进发射方式相比具有明显的技术优势[2]。
电磁线圈发射方式作为电磁发射技术的重要分支,可实现电枢与驱动线圈无电气和机械直接接触,还具有可控性好、效率高、寿命长等诸多优点[3],可达到较高发射初速、易发射大质量物体,与舰载深弹武器系统有着很高的契合度,在海洋攻防上具有良好的应用前景[4]。
弹道性能仿真在方案设计、射表编制、模型验证、作战仿真中都有广泛而重要的应用[5]。因此,分析电磁发射深弹弹道性能对开展电磁发射深弹的研制工作具有重要的参考意义。
本文利用MATLAB/Simulink软件建立了六自由度刚体弹道方程,运用蒙特卡洛方法建立了地面密集度的仿真预测模型,着重论述了电磁发射深弹在一定发射动能条件下的射程覆盖范围。同时,综合考虑影响电磁发射深弹地面密集度的各种误差因素,对深弹最大射程、最小射程下的落点误差进行了仿真,分析了各种误差因素对电磁发射深弹射程、方向中间误差的影响程度。仿真结果可为电磁发射深弹及类似电磁发射弹的论证研究提供一定的技术参考价值,其弹道算法可用于电磁发射深弹方案研究。
1 数学模型与分析
1.1 弹道模型
本文弹道模型选用文献[4]给出的六自由度刚体弹道方程。该方程具有精度较高的特点,能完整描述电磁发射深弹在空中的各种动态过程,可用于弹道射程及落点误差的影响因素分析。
为简化模型,对深弹及飞行条件作如下假设[6]:
1)电磁发射深弹是一个外形和质量分布均匀且轴对称的刚体;
2)气象条件是标准的,风速恒定;
3)重力加速度恒定不变;
4)忽略科式惯性力的影响。
1.2 发射动能
电磁发射深弹依靠发射装置产生电磁力加速运动,受到发射装置电源系统[7]的制约,电磁发射深弹存在最大的发射动能Emax。
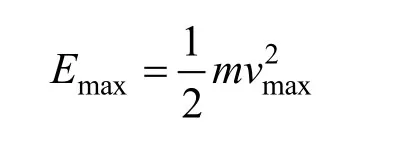
式中:m为电磁发射深弹设计质量;vmax为电磁发射深弹的最大发射速度。
东西使用恰当,能够让事情展现出超过预期的价值。国人能发挥人的主观能动性,东西差,但技术很好,能够把东西用活,给人带来快乐,是人驾驭物的最高境界。物作为载体,要了解给使用者带来的价值大小,可以去衡量使用者的感受。物只是让人们聚集在一起有个理由,不在乎物怎样,大家相聚在一起便是开心,这是追求精神层面需求的过程。物是要被人所使用的,只是一个载体,所做的事本身也只是让人们努力有一个方向,不必太过执着。对物的过分执着却是在需求层次的物质底线挣扎。自我实现,可以是在物质贫乏的时期,进行一段化腐朽为神奇转变。海归新生代企业家在企业经营活动中,不应只强调工作本身,应该多加考虑参加工作的人的感受。
在最大发射动能Emax条件下,可以根据总体设计需求,合理匹配深弹设计质量m和最大发射速度vmax,来实现深弹的最大射程。同时,在深弹设计质量m确定的情况下,可以通过调节发射动能,改变发射初速,来实现不同的弹道射程,而不需要改变发射射角。
1.3 弹道密集度
根据概率论中心极限定理,弹道射程和侧偏的概率密度服从正太分布。
在弹道学中,通常用中间误差E表示射程和侧偏的分布。随机变量出现在均值μ左右各1个E范围内的概率为50%,这个E被称为中间误差。在均值左右4E(共8E)或3σ(共6σ)范围内,随机变量出现的概率大于99%,近似为1。
n发弹中第i发弹的射程和侧偏分别为xi、zi,密集度为Ex/xa、Ez/za。其均值xa、za,均方差σx、σz和中间误差Ex、Ez的计算公式分别为

根据外弹道学理论,由初速、射角及弹道系数这3个参量即可得到1条确定的弹丸质心弹道。在弹丸发射过程中,各种随机因素使得各发弹之间的初速、射角及弹道系数的值存在微小的随机差异,这是形成弹丸散布的根本原因[8]。其中,弹道系数的随机变化是由弹丸质量、弹径和弹形系数引起的,而后者又与弹表光滑程度及攻角的大小和变化情况有关。本文对影响电磁发射深弹落点散布的随机因素进行了一些简化,同时根据实际情况引入了横向起始偏角和风的影响[9]。
2 仿真流程及仿真结果分析
电磁发射深弹弹道性能仿真流程如图1所示。
2.1 仿真条件
假设电磁发射装置最大发射动能为1.5 MJ,对电磁发射深弹的弹道性能进行仿真分析。
2.2 最大发射动能下的弹道射程
根据最大发射动能公式,计算出电磁发射深弹的设计质量与最大速度的变化关系,如图2(a)所示。随着设计质量的增加,电磁发射深弹可获得的最大速度呈二次方关系衰减。
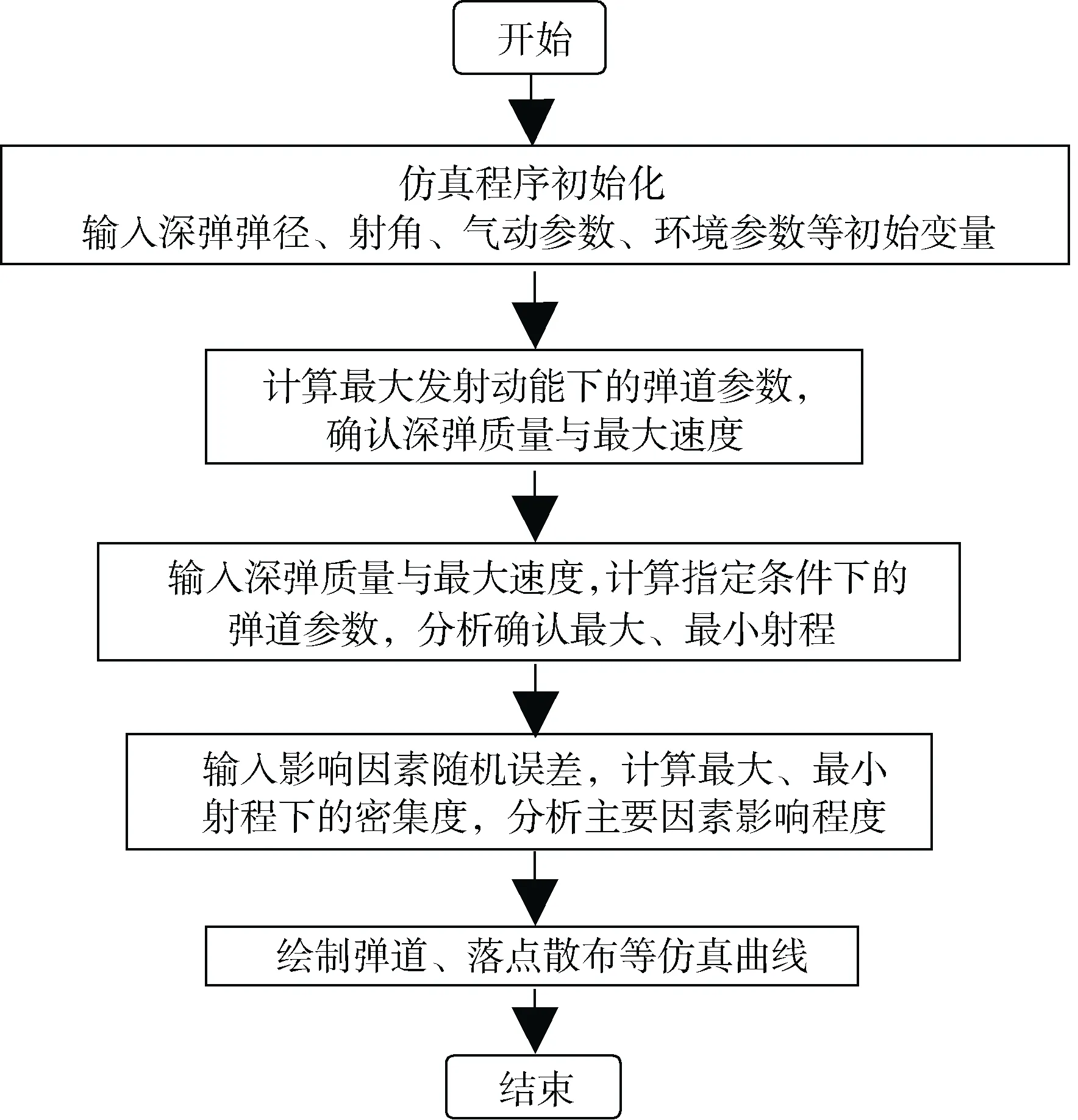
图1 仿真分析流程Fig. 1 Simulation analysis process
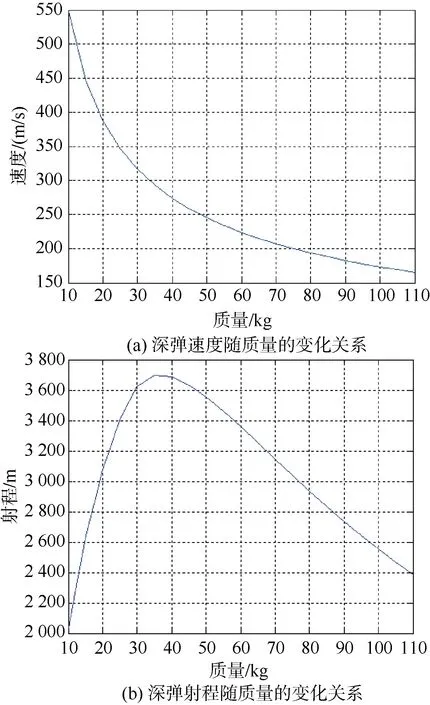
图2 最大发射动能时深弹速度、射程随质量的变化关系Fig. 2 Variation of depth charge’s velocity and range with mass under maximum kinetic energy
将图2(a)所示的电磁发射深弹设计质量、最大速度以及传统火箭发射深弹的相关设计参数代入弹道方程,计算出电磁发射深弹不同设计质量下的弹道射程,如图2(b)所示。
根据计算,电磁发射深弹在最大发射动能的限制下,随着自身设计质量的增加,其弹道射程先增大后减小,存在最优值。如图2(b)所示,深弹设计质量为35 kg、最大速度为292.8 m/s时,弹道射程最大,约3 695 m。
结合电磁发射深弹总体性能设计要求,可以基本确定电磁发射深弹的设计质量和最大速度。本文取设计质量为70 kg、最大速度为207 m/s进行研究。
2.3 最大射程、射角的确定
将2.2节确定的电磁发射深弹设计质量和最大速度代入弹道方程,计算出不同射角下的弹道射程和飞行时间,如图3所示。
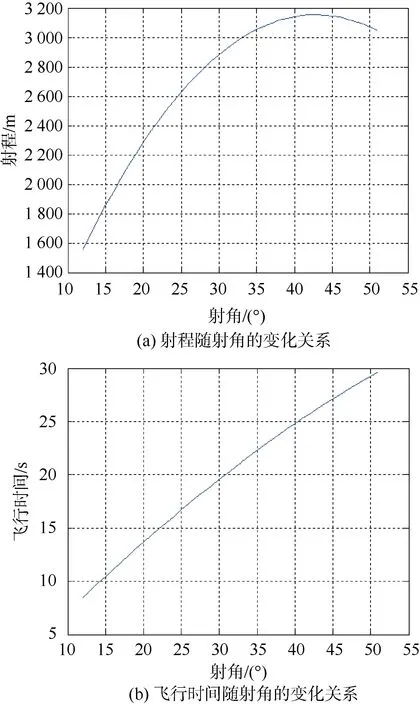
图3 深弹射程和飞行时间随质量的变化关系Fig. 3 Variation of depth charge’s range and flight time with mass
根据计算,深弹的弹道射程随着角度的增加,先增大后减小。射角在40°~45°之间,弹道射程的变化最小;射角约43°时,射程最大,约为3 154 m。深弹的飞行时间与射角的变化曲线基本呈一次线性的正比例关系。
为了尽量减少电磁发射深弹的作战反应时间,本文选定40°射角作为电磁发射深弹的固定射角进行研究。通过仿真计算可得,电磁发射深弹的最大射程为3 141 m,最大射高为756 m,飞行时间为24.8 s,落点速度为152.4 m/s,落点角度为-47.9°,最大攻角为0.34°。图4为40°射角下的最大射程弹道速度及俯仰角曲线。
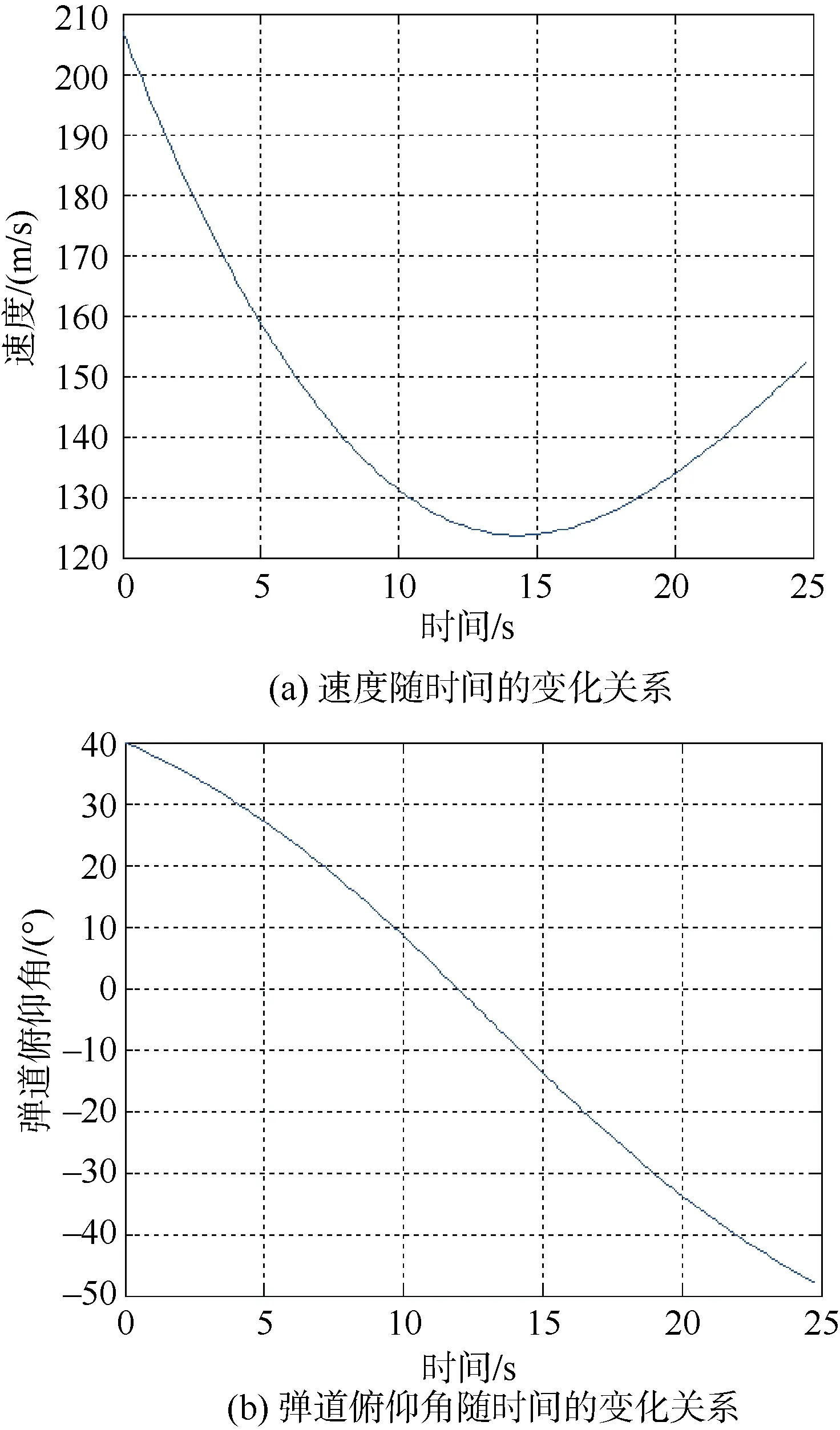
图4 最大射程弹道速度及俯仰角曲线Fig. 4 Depth charge’s velocity and angle of pitch at maximum firing-range
2.4 最小射程、射速的确定
电磁发射深弹在飞行过程中,仅依靠气动力矩稳定飞行。由于气动力矩与飞行速度的二次方成正比,速度减小会大幅降低气动稳定力矩,因此深弹的最小射程发射速度必须设定下限,以免飞行速度过低、气动稳定力矩不足而导致飞行失败,或者攻角太大导致引信击水机构工作失败、可靠性降低。
根据以上原因,仿真计算了深弹在射角为40°时,不同发射速度下的弹道攻角、弹体俯仰角的变化曲线,如图5所示。
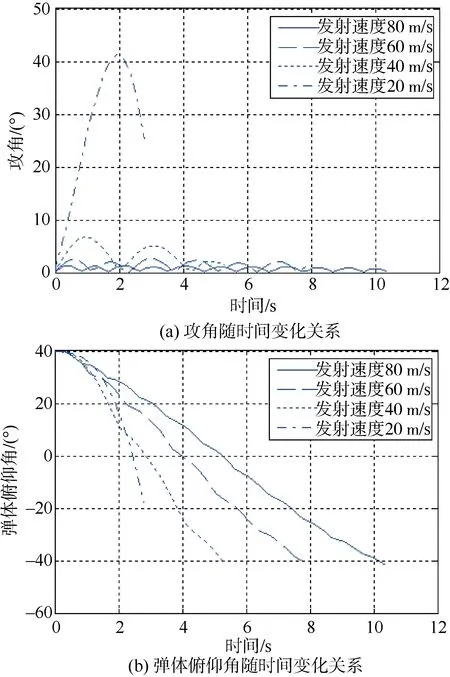
图5 不同发射速度下,攻角和弹体俯仰角随时间变化关系Fig. 5 Variation of depth charge’s angle of attack and angle of pitch with flight time at different launching speed
根据计算,深弹发射速度降低时,其弹道攻角幅值逐渐增大,弹体俯仰角变化越来越剧烈。发射速度在80 m/s、60 m/s、40 m/s、20 m/s时,弹道攻角的最大值分别达到了1.3°、2.6°、6.7°、41.3°,弹体俯仰角的最终值在发射速度为20 m/s时仅达到-19°左右,入水条件对深弹水下工作性能非常不利。不同发射速度下的深弹入水角度和速度如表1所示。
本文选定60 m/s作为电磁发射深弹的最小射程发射速度,通过仿真计算可得:电磁发射深弹的最小射程为355 m,最大射高为77 m,飞行时间为7.9 s,落点速度为58.2 m/s,落点角度为-41.5°,最大攻角为2.6°。图6为60 m/s条件下的最小射程弹道速度及俯仰角曲线。

表1 不同发射速度下深弹入水角度和速度统计表Table 1 Depth charge’s water entry angle and velocity under different launching speed
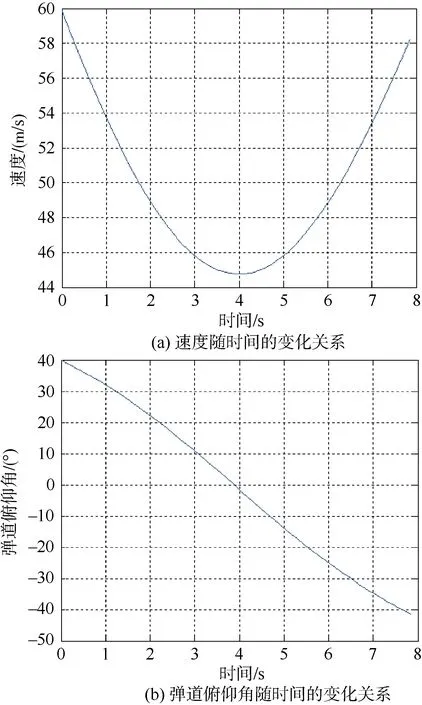
图6 最小射程弹道速度及俯仰角曲线Fig.6 Depth charge’s velocity and angle of pitch at minimum firing-range
2.5 密集度性能
影响电磁发射深弹地面密集度的主要因素有:初速误差、初始射角误差、质量误差、横向起始偏角误差、风速误差等。假设各误差因素均服从正态分布,中间误差选取如下:
1)初速由电磁发射装置性能决定,假定初速中间误差Ev0是初速的0.3%;
2)初始射角与横向起始偏角误差取决于发射装置性能,假定两者中间误差Eθ0与EΨ0均为0.2°;
3)质量由装配工艺决定,中间误差Em0取0.15 kg;
4)风速中间误差Ew取2 m/s。
利用蒙特卡洛法地面密集度仿真模型,按上述误差因素的分布规律生成伪随机数,分别仿真1 000次,计算电磁发射深弹最大、最小射程中间误差及各误差因素的影响程度,如表2和表3所示。
由表2和表3所示,电磁发射深弹最大射程落点误差主要受初速误差、横向起始偏角误差、风速误差影响。初速误差对射程中间误差的影响程度最大,达到了77.1%;横向起始偏角误差对方向中间误差的影响程度最大,达到了87.2%;风速误差对射程、方向中间误差的影响程度分别达到了28.1%和10.5%。电磁发射深弹最小射程落点误差主要受初速误差和横向起始偏角误差影响。与大射程各误差因素影响程度相比,初速误差和横向起始偏角误差的影响程度明显增大。其中,初速误差对射程中间误差的影响程度达到了96.2%;横向起始偏角误差对方向中间误差的影响程度达到了105.2%(此处计算值超过100%是由于不同射程下的射程、方向中间误差均采用蒙特卡洛方法独立计算,存在随机统计误差的原因,真实值应小于100%);风速误差的影响程度明显减小,其对射程、方向中间误差的影响程度分别下降至3.4%和1.6%。

表2 不同射程下射程中间误差及各因素所占比例Table 2 The ratio of firing-range intermediate error and various error factors at different ranges

表3 不同射程下方向中间误差及各因素所占比例Table 3 The ratio of directional intermediate error and various error factors at different ranges
电磁发射深弹最大射程、最小射程各1 000发的落点散布情况分别如图7所示。根据计算,最大射程的纵向密集度为1/191,横向密集度为1/208,最小射程的纵向密集度为1/171,横向密集度为1/226。最大、最小射程密集度值相差不大,但由于小射程的射程近,其落点误差明显优于大射程。
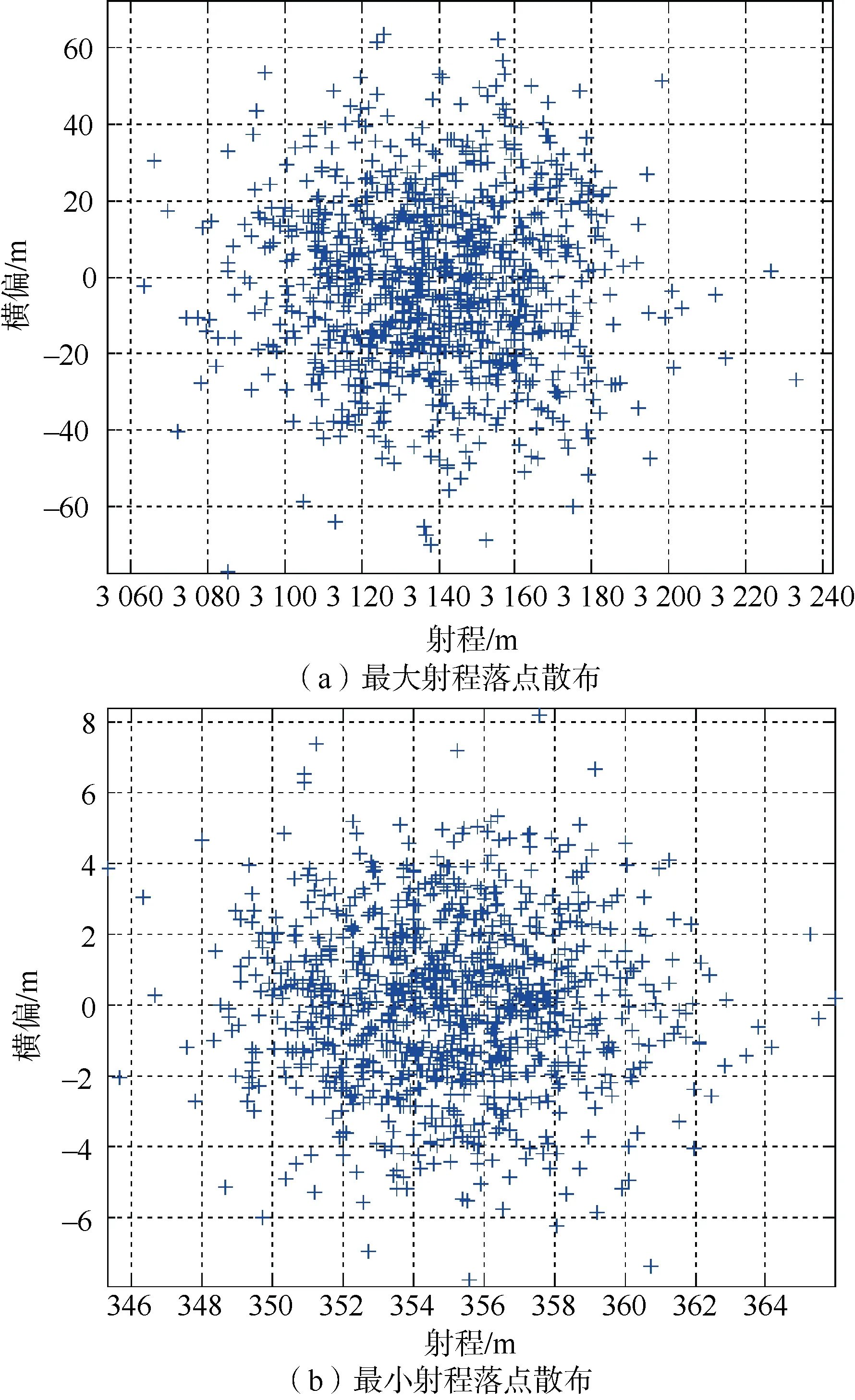
图7 最大射程和最小射程落点散布Fig.7 Dispersion of fall point at maximum firing-range and minimum firing-range
3 结束语
通过上述分析及仿真实验,可得到如下结论:
1)在电磁发射装置最大发射动能的限制下,电磁发射深弹的最大射程存在最大值。
2)在电磁发射装置发射角限定的条件下,不能通过一味的降低发射速度来降低弹道射程。发射速度降低到一定程度后,会严重影响弹道稳定性。因此,电磁发射深弹也须设定最小射程。
3)电磁发射深弹的落点误差主要与初速误差、横向起始偏角误差、风速误差有关。随着射程的降低,初速误差与横向起始偏角误差的影响程度增大,风速误差的影响程度减小。
