封锁战役中攻势布雷任务优化分配模型
2020-06-12董世海
董世海
(中国人民解放军92942部队,北京 100161)
0 引言
海上封锁战役中,水雷障碍封锁配系是整个封锁体系的重要组成部分,可以达成一定的战略、战役目的,对战争全局产生重大影响,实现“不战而屈人之兵”。攻势布雷作战行动涉及大量的布雷兵力、作战支援保障兵力的使用,以及水雷武器的消耗。由于布雷平台和水雷的类型数量、出航港口或机场、被封锁的敌港口目标、封锁程度等不同,构成了数量巨大的布雷任务分配组合。布雷任务分配组合的合理与否将直接影响到整个障碍封锁配系的作战效能。
国内目前对于任务分配优化模型研究有一定的基础,但主要集中于火力打击领域[1-4]或运输任务[5];对于布雷任务,主要集中于水雷障碍战术层级的毁伤计算[6-8],也有提出建设布雷决策系统的构想[9],提出系统框架结构,但未建立相关具体数学模型;对于战役层级水雷障碍封锁任务分配或封锁评估的研究相对较少。从战争的消费比和封锁战役的可维持性来看,必须对攻势布雷作战任务进行优化设计,实现水雷障碍封锁的高效费比;从封锁战役筹划的角度,应自足现有的布雷兵力、水雷兵器情况,准确衡量障碍封锁能力,合理确定水雷障碍的封锁指标。因此,使用规划论的方法对封锁作战中攻势布雷任务进行优化分配,具有一定的应用价值。
1 攻势布雷任务分配问题分析
1.1 基本问题
海上封锁战役中,会赋予水雷障碍具体的封锁指标,或完全由水雷障碍来达成封锁战役指标。攻势布雷任务优化分配问题分为2类:1)最大限度节省资源投入问题,即当现有水雷兵器和布雷兵力充足,可达成规定的封锁指标,寻求成本最小时的任务规划问题;2)现有资源的利用达到最大化问题,即当现有水雷兵器或布雷兵力不足,无法达成规定的封锁指标,寻求封锁效能最大时的任务规划问题。基本问题就是上述2类情况下,选择各机场或港口所部署的何种类型布雷平台,以及选用何种类型的水雷对敌港口实施水雷障碍封锁的任务分配问题。目的是求出布雷兵力的任务分配矩阵,假设我方自港口或机场i使用j型布雷平台对敌港口l布设k型水雷的数量为nijkl,则矩阵N=[nijkl]即为布雷任务分配矩阵。
1.2 要素间相互影响关系分析
封锁战役中攻势布雷任务优化分配的目的就是如何发挥整体优势,把我方水雷布设至敌方港口外,达到最大的障碍封锁效果。可把各港口运输舰船所通过的水雷障碍区触雷概率作为联系布雷任务和封锁效果之间的中间变量来看,原因有2个:1)封锁效果用敌航运的下降程度来表示,敌航运的下降是由于受到水雷障碍的威慑和毁伤造成的,可用触雷概率的大小进行测算;2)各港口的触雷概率大小可转化为对布设于该雷区的水雷类型和数量的需求,以及对布雷平台类型和数量的需求。由于敌港口的防御重点、严密程度不同,导致不同港口或机场出航的各型布雷平台所面临的威胁程度不同、布雷成本也不同,所以,要求必须结合敌各港口防御和航运实际以及地理环境特点来对布雷平台的使用、水雷的选择进行优化。
1.2.1 触雷概率与航运降低程度之间的函数关系
由于组成各港口航运系统的船舶性质、类型、数量等不同,所以各港口的航运降低程度与触雷概率之间的函数关系不同。水雷障碍对敌运输舰船的作用体现为威慑和毁伤,分2步进行分析:1)对不同的触雷概率下,因威慑而停运的各型舰船比例可采用效果期望理论或累积前景理论进行定量分析,建立单港口因水雷威慑而导致的航运降低程度与触雷概率之间的曲线关系,进而拟合出其分布函数Q(P);2)综合水雷威慑和毁伤对运输舰船的影响,当触雷概率为P时航运的总下降程度为
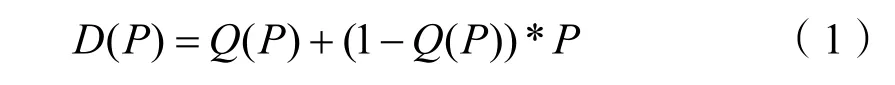
1.2.2 触雷概率与水雷数量之间的函数关系
通常认为,对敌进行封锁攻势布雷的雷区为不规则水雷障碍。水雷在全雷区范围内大体上是均匀分布的,所以敌运输船在雷区内遭遇水雷的概率可选用泊松公式表示,则敌在雷区中触雷概率为

式中:λ为水雷障碍区内水雷平均密度;ω为舰船穿过雷区的面积,即ω=2×r×s,r为水雷打击半径,s为舰船在雷区中的航程。
因水雷障碍区必须有足够的遮拦宽度B,以确保对港口的全面封锁;敌运输舰船在雷区中航行,必定以垂直穿过雷区为其首选,此时遭受的水雷威胁最小。敌舰船在雷区中的航程s即等于水雷障碍区的纵深,则需处于战斗状态的水雷数量n与触雷概率P的关系为

2 攻势布雷任务优化分配模型构建
攻势布雷任务优化分配问题可抽象为整数规划问题,以整数规划作为任务分配模型的核心理论。
2.1 第1类问题的模型构建
2.1.1 确定目标函数
根据对资源投入的不同理解,可初步确定为3类基本的目标函数,可单独使用或组合使用。
1)最小化的布雷平台总出动价值。

式中:Z1表示最小的布雷平台总出动价值;I、J、K、L分别表示我方港口或机场、布雷平台型号、水雷型号、敌方港口的总数;DVjl表示j型单布雷平台至敌港口l执行1次布雷任务的出动价值;Djk表示j型单布雷平台可载k型水雷的数量(假定单布雷平台每次执行布雷任务时只载1个型号的水雷,且同型布雷平台载同型水雷的数量相等)。
2)最小化的布雷平台总损耗价值。

式中:Z2表示最小的布雷平台总损耗价值;WAijl表示j型布雷平台自港口或机场i出航对敌港口l执行布雷任务的战损率;DWj表示j型单布雷平台被击毁时损耗价值。
3)最小化的水雷总投入价值。
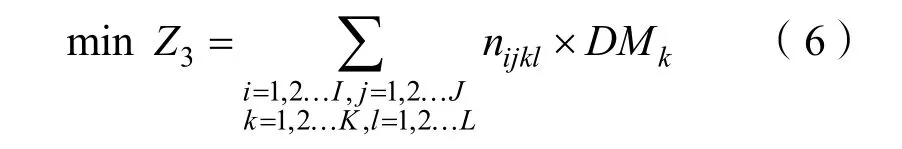
式中:Z3表示最小的水雷总投入价值;DMk为单枚k型水雷的价值。
2.1.2 确定约束条件
1)封锁指标约束。
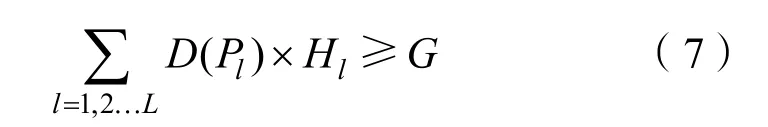
式中,D(Pl)表示敌港口l航运下降程度与所遭遇水雷障碍的触雷概率Pl之间的函数关系。
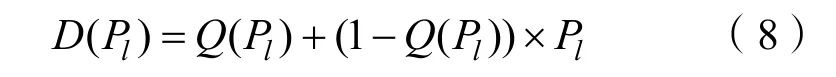
关于lP与水雷数量nl之间的函数关系分析如下:
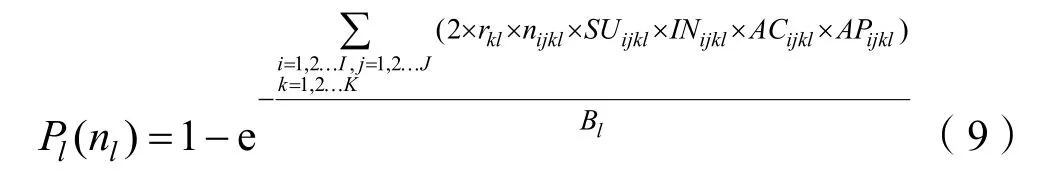
式中:rkl为k型水雷在敌港口l外水文地理环境下的打击半径;Bl为封锁港口l的水雷障碍遮拦宽度;SUijkl、INijkl、ACijkl、APijkl分别表示由港口或机场i出航的j型布雷平台对敌港口l布设k型水雷的布雷行动成功率、水雷安好率、进入战斗状态且定次为1的水雷比例、打击概率,0≤SUijkl、。
Hl表示敌港口l的航运量占被封锁方总航运量的比重,可列式:进行计算,HTl为港口l的航运量。
G为上级所赋予的总的封锁指标,若对某些港口有具体的封锁指标,则将各封锁指标约束分别列出,即有

2)布雷平台力量约束。
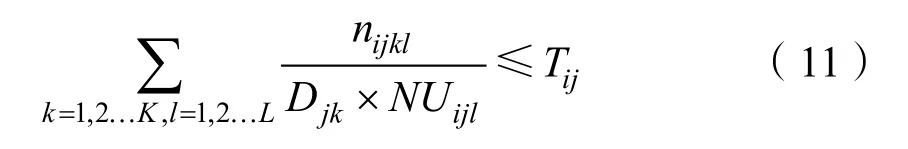
式中:Tij表示港口或机场i可执行布雷的j型布雷平台的数量;NUijl表示由港口或机场i出航的j型布雷平台在规定时间内对敌港口l进行布雷的平均出动次数。
若要求1次完成布雷任务μ=1或该布雷平台为一次性布雷平台WAijl=1,则NUijl=1;若在规定时间内,可进行μ次布雷,则
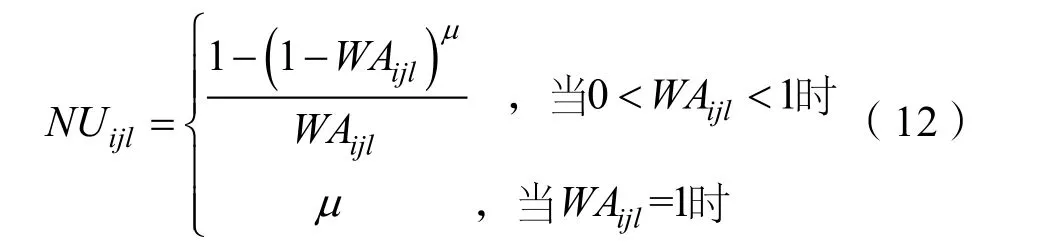
3)布雷平台损耗约束。
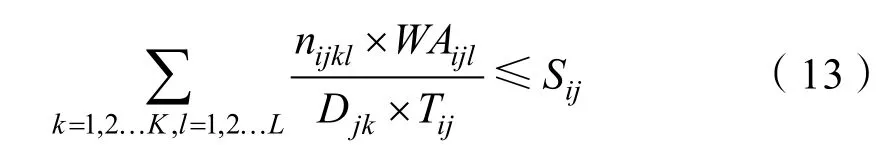
式中,Sij表示上级规定的港口或机场i的j型布雷平台的损耗百分比指标。
4)水雷数量约束。

式中,Mik表示港口或机场i所拥有的k型水雷的数量。
2.2 第2类问题的模型构建
2.2.1 确定目标函数
由于在原约束条件下无法达成障碍封锁指标,第2类问题的目标函数应为满足布雷兵力和水雷兵器使用条件下寻求最大的封锁效能。为此,建立目标函数:

式中,G′为立足现有约束条件下的最大封锁指标,即所能实现的对敌航运系统的最大封锁程度。
2.2.2 确定约束条件
布雷平台力量约束、布雷平台损耗约束、水雷数量约束与第1类问题的约束条件相同;各参数、函数的定义与第1类问题中的定义相同。
此外,应立足于敌情、我情和战场环境实际,将我方布雷行动损失大、效能低的敌港口布雷任务调整为改由其它作战行动样式,如对敌火力封锁、对敌港口的火力打击、对敌陆上重要交通枢纽或交通线的火力打击等,来实现敌航运程度的降低,以确保现有水雷、布雷能力的最大作用发挥。此时,可对调整后的障碍封锁能力进行重新计算,若可实现障碍封锁指标,则按第1类问题的模型计算最佳方案;若仍不能实现障碍封锁指标,则按第2类问题的模型计算最佳方案。
3 关于模型数据的筛选问题[1]
对于确定的作战想定,模型内变量的数据量很大,应使用模型外的约束,对数据进行预处理,分析港口或机场与部署的布雷平台、布雷平台与水雷类型、布雷平台与敌港口、水雷类型与敌港口等之间联系的可能性,删除不可行数据,以提高模型的运算速度和结果的可行性。具体分析如下。
1)删除港口或机场部署布雷平台的不可行数据。
攻势布雷行动在一定程度上可将水面舰艇布雷的可行性排除在外。对于机场,只可能部署空中布雷平台,如轰炸机、歼轰机或空中无人布雷平台等,而不可能部署水下布雷平台;对于港口,只能部署水下布雷平台,如潜艇、水下无人布雷平台等,而不能部署空中布雷平台。删除此类数据,可有效降低nijkl中下标为i、j的数据量。
2)删除布雷平台装载水雷类型的不可行数据。
布雷平台与水雷类型之间是有相互联系的,某型布雷平台仅能布设其中1种或几种水雷障碍,某型水雷也仅能由其中1种或几种布雷平台布设。以自航式水雷为例,通常仅能由潜艇布设,而空中布雷平台、水下无人布雷器等无法布设或应用意义不大;航弹式水雷,通常由空中布雷平台布设,而水下布雷平台却无法布设。删除此类数据,可有效降低nijkl中下标为j、k的数据量。
3)删除布雷平台对敌港口封锁的不可行数据。
主要有:①组织对敌某港口布雷行动,已超出我方部署于某港口或机场的某布雷平台活动半径,且无法组织中途油料补给时,则无法使用该平台组织对该港口实施布雷;②敌对某港口防御极为严密,使用某布雷平台战损率极高,可确定某一指标值,战损超过此值的予以删除;③港口环境不满足某布雷平台使用条件,如水深限制潜艇活动等。删除此类数据,可有效降低nijkl中下标为i、j、l的数据量。
4)删除水雷类型与对敌港口封锁的不可行数据。
受港口外水文地理环境的限制,某些水雷可能不适宜布设于敌方某些港口外,如水深较深时,沉底水雷打击效果将大大降低;或受引信限制,该海区不适合于布设该型水雷等。删除此类数据,可有效降低nijkl中下标为k、l的数据量。
优化模型外的上述约束内容,是需要计划拟制人员依靠自身经验进行确定的,尽管删除此类数据较为繁琐,需要结合实际进行逐一考虑,但却可以有效降低计算的数据量,能为迅速准确确定最优布雷任务分配方案发挥重要作用。
4 案例分析
本节以1个简单案例介绍上述模型的使用。假定红方从某机场起飞的3型飞机拟对蓝方A、B、C 3个港口组织1次集中布雷,红方布雷能力见表1,蓝方港口和航运情况见表2,分析红方对蓝方的最大封锁程度以及优化布雷任务。为避免出现单架次飞机执行任务,各型飞机按2架为1编组进行计算,并假定红方机场可保障甲型、乙型水雷,且2型水雷数量充足。
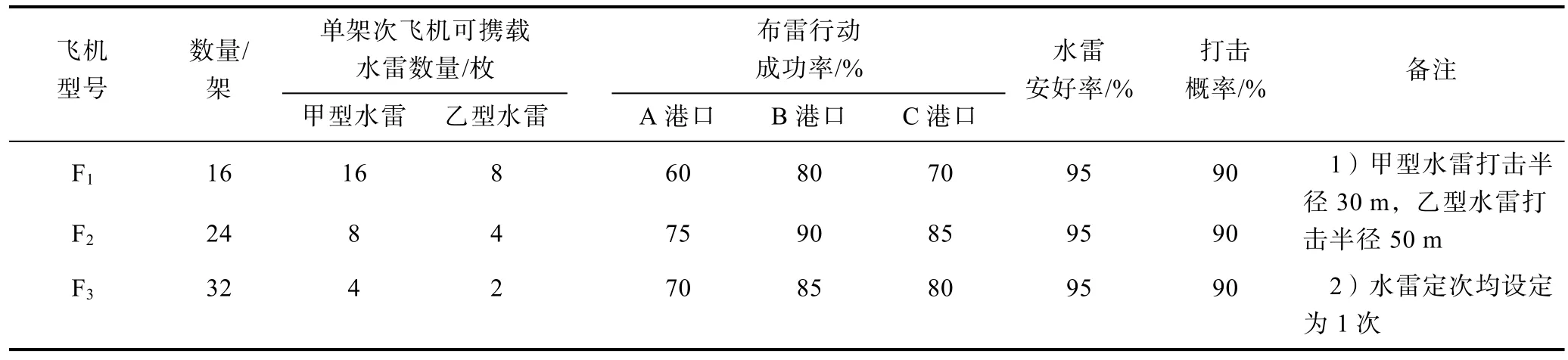
表1 红方布雷能力Table 1 The RED’s mine-laying capability

表2 蓝方港口和航运情况Table 2 The BLUE’s port and shipping information
该问题属于第2类问题。1)先分析若红方所有布雷平台分别对蓝方3个港口实施攻势布雷所达到的封锁程度,经计算分别为0.300 6,0.877 8,0.838 0,即对蓝方整个航运的封锁程度为0.150 3,0.175 6,0.251 4,均未能达到对蓝方实施封锁的目的指标;2)分析如何实现布雷任务最优化,以达到最大的封锁程度为目的指标,根据第2类问题的模型,求解可得最大封锁程度为0.276 3。布雷平台兵力分配见表3,布雷均为甲型水雷。
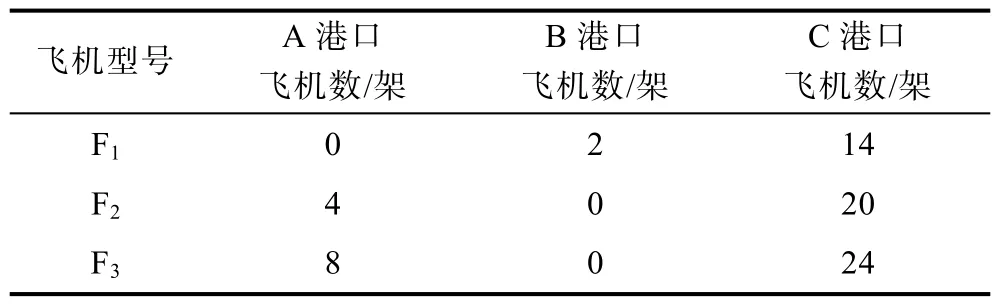
表3 布雷平台兵力分配Table 3 Distribution of mine-laying platforms
为进一步分析水雷障碍威慑作用在封锁战役中的效能发挥,通过调整反映水雷障碍威慑作用的变量值,计算结果如下文所示。通过对比发现,通过舆论造势,增加航运管理者的心理压力等,在同等封锁条件下,可有效增大封锁程度。
情况A:关于迫使蓝方航运船舶放弃航运的触雷概率,若通过舆论造势等,使其对此所认为的触雷概率较实际值大0.2,则红方所有布雷平台分别对蓝方3个港口实施攻势布雷所达到的封锁程度分别为0.790 2,0.877 8,0.838 0,可实现对蓝方最大封锁程度为0.460 0。布雷平台兵力分配见表4,布雷均为甲型水雷。
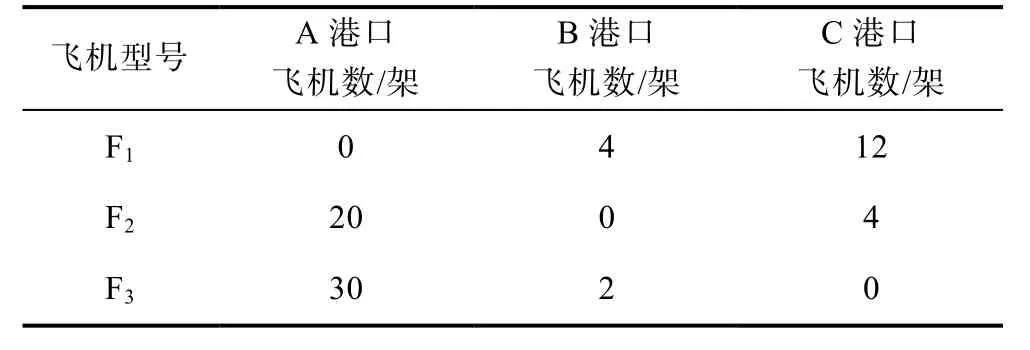
表4 情况A下的布雷平台兵力分配Table 4 Distribution of mine-laying platforms in Case-A
情况B:若在水雷威慑下仅有50%的船舶放弃航运,则红方所有布雷平台分别对蓝方3个港口实施攻势布雷所达到的封锁程度分别为0.300 6,0.796 4,0.730 0,可实现对蓝方最大封锁程度为0.240 3。布雷平台兵力分配见表5,布雷均为甲型水雷。
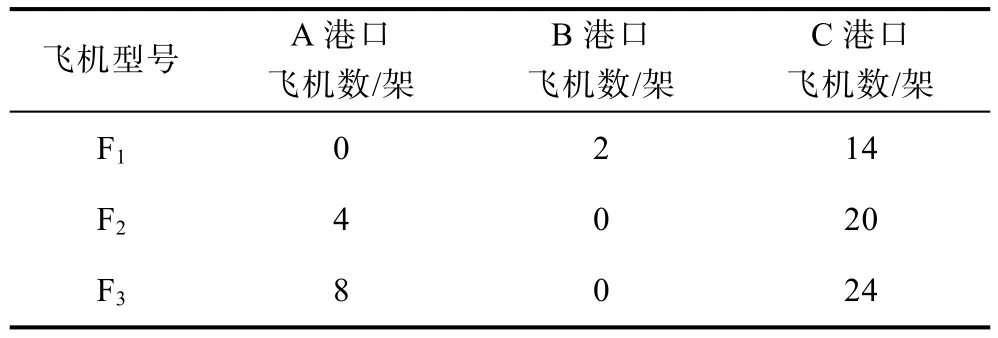
表5 情况B下的布雷平台兵力分配Table 5 Distribution of mine-laying platforms in Case-B
情况C:若在水雷威慑下仅有50%的船舶放弃航运,通过舆论造势等,使其对此所认为的触雷概率较实际值大0.2,则红方所有布雷平台分别对蓝方3个港口实施攻势布雷所达到的封锁程度分别为0.650 3、0.796 4、0.730 0,可实现对蓝方最大封锁程度为0.376 1。布雷平台兵力分配见表6,布雷均为甲型水雷。
表6 情况C下的布雷平台兵力分配Table 6 Distribution of mine-laying platforms in Case-C
5 结束语
海上封锁战役中攻势布雷任务优化问题是一个较为复杂和困难的问题,涉及的布雷平台和水雷的型号杂、数量多,且出航地不同、对敌封锁的港口不同使得对布雷平台和水雷的需求也不尽相同,导致出航地、布雷平台、水雷、敌港口之间的组合多,依靠人工去进行布雷任务优化分配是很困难的。本文采用规划论的方法,分别对2类问题构建了布雷任务优化的模型,可为制定封锁战役计划提供定量分析的方法工具,具有较大的适用性和可操作性。
