基于神经网络的精神分裂fMRI数据分类

黄庆坤 杨鹏

(大理护理职业学院 云南省大理市 671000)

大脑作为人体最高级神经控制中枢，一直以来都是神经科学、医学和生物信息学领域研究人员的研究热点。功能磁共振成像技术(Functional Magnetic Resonance Imaging，fMRI)凭借高效无创等特性，可用于解读大脑的工作机理以及判别各种脑相关的潜在患病机制。因此怎样分析fMRI数据，选取合适的分类特征构建分类器，成为了fMRI数据分类的关键。Osmar等人[1]在医学图像的检测中使用了聚类方法从此提出fMRI数据分类的概念，在对于精神分裂fMRI的研究中，Fan等人[2]通过主成分分析法(PCA)和支持向量机(SVM)分类原理对精神分裂fMRI进行数据分类，提出精神分裂患病机制可能由于潜在的脑结构和脑结构的异常所导致；Firat等人[3]在深度网络中使用到了一种自稀疏编码的方法，来对大脑的认知状态进行解码。

从前人的研究工作来看，对于高维fMRI数据研究采用了特征提取与分类算法相结合的思路，因此存在着特征提取与算法择优的问题。传统机器学习大多都为浅层模型,并且对高维fMRI数据存在着不能有效提取特征的问题,并且需要对一般的分类算法进行优化改进。本文结合精神分裂fMRI数据集，在大脑内通过字典学习与区域提取算法划分感兴趣区域，并提取时间序列通过皮尔逊相关系数进行相关性分析，通过特征降维结合神经网络算法进行分类研究，从脑功能连接的角度出发，更好的辅助临床诊断。

1 相关方法

1.1 皮尔逊相关系数

皮尔逊相关系数由英国数学家Pearson提出，用于计算变量之间的线性相关程度，对于多维随机变量，两两维度的皮尔逊相关系数p(xi,xj)可描述为：

其中，σ(xi)和σ(xj)分别为xi和xj之间的标准差，cov(xi,xj)为xi和xj之间的协方差，其中cov(xi,xj)可描述为：

在（2）式中，变量xi和xj之间的相关性与协方差的绝对值成正比，可等价写作：

其中，P(xi,xj)∈(-1,1)。从（3）式中，我们可以看到xi和xj两个变量之间的线性相关性越强，其值越接近-1（负相关）或越接近1（正相关），越接近0则相关性越弱，因此皮尔逊相关系数可用于多维随机变量的相关性分析。

1.2 神经网络分类模型

在N个样本数据集N={(x1,y1),(x2,y2),…,(xn,yn) },xi,yi∈R，其中x1,…xn为样本的n个特征维度，y1,…yn为样本的实值向量，神经网络模型通过训练feature(x1…xn)来获得label(y1…yn)。假设表示第L层的第j个神经元输入，为第L层第p个神经元的输出，表示第L层第i个神经元与第L+1层第j个神经元的权重，表示第L层第i个神经元的偏置值。通过输入层的值，可以计算隐藏层与输出层的值：

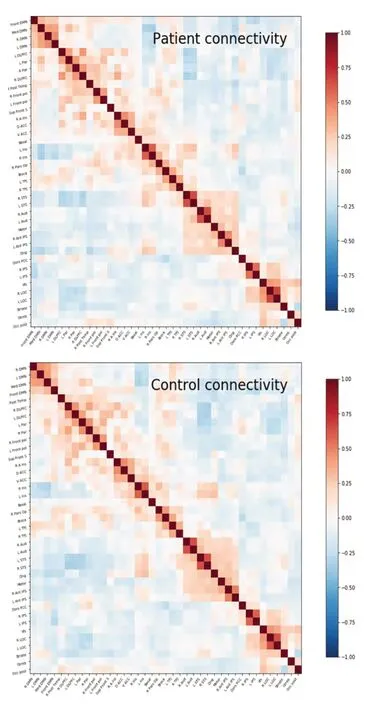
图1

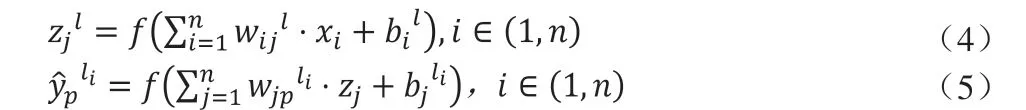
通过梯度下降算法，模型训练让样本的输入值接近真实值，即E→0。对权值与偏置进行学习，求出各层更新量

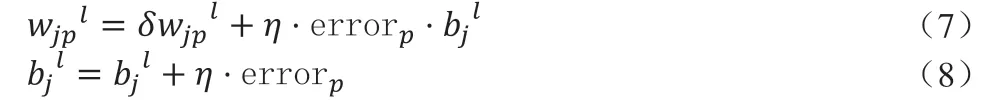
其中，λ>0，为L2正则化参数通过。确定λ的值可以使得在方差和偏差之间达到平衡，随着λ的增大，模型方差减小而偏差增大。

2 实验及结果分析

2.1 数据及预处理

Cobre数据集是(The Center for Biomedical Research Excellence,COBRE)为72名被诊断患有精神分裂症和74名健康对照提供原始解剖和功能性MR数据，每个受试者的fMRI数据集是单个nifti文件（.nii.gz）,FOV=240mm×240mm,slices thickness =3.5mm,plan size= 64×64,voxel size=3.75mm×3.75mm× 4.55mm)。在cobre数据集中，我们首先通过spm8工具包对cobre脑影像数据进行预处理，经过头动校正、时间校正、标准化、并采用高斯核的全宽半高FWHM=8来对图形进行平滑化处理。

2.2 特征分类

实验采用多学科字典学习与区域提取算法得到Atlas脑分区模板[4]，将大脑区域划分为39个感兴趣区域（ROI）。在146个被试中提取39个ROI的时间序列得到一维时间和一维特征矩阵。提取ROI的时间序列后，我们计算每个ROI之间的功能网络连接性的皮尔逊相关系数，并进行Fisher-Z变换得到相关系数矩阵，来量化大脑不同脑区之间的连接强度。在此基础上，我们通过PCA降维方法对其进行特征提取，并构建神经网络分类器，在实验中，通过交叉验证后分类准确率如表1。

从表中,我们可以看到在两个含有隐藏层的神经网络中对于测试集分类准确率为76.3%，优于文献[5]的准确率65%和文献[6]的准确率70.5%，并且对比其他算法的分类效果除了在多个隐藏层节点下无法较好对样本集较好预测(分类准确率不足60%)外,其他分类算法可较好的完成分类任务，即使在随机确定参数的情况下，效果也比其好很多。

2.3 结果分析

提取参与训练的精神分裂症患者和正常被试的分类脑区特征，并通过皮尔逊相关系数构建相关系数矩阵，如图1所示。

图1中横纵坐标分别代表39个ROI的名称，对应坐标值为脑区之间的相关性，皮尔逊相关系数值接近在颜色柱两端，代表特征之间的相关性越强,浅色区域皮尔逊相关系数值为0，代表特征之间不相关，特别地对角线元素值为1，在一些ROI区域之间连接强度存在差异，这些区域主要集中在双侧小脑下叶、颞下回、壳核、尾状核和海马旁回等部位，另外在精神分裂症患者中，枕叶和小脑的有向连接相比正常人的连接更强。同时，枕叶和小脑之间的因果连接在患者中也更强。基于分类特征，我们分析相关性矩阵的平均加权聚类系数、平均特征路径长度以及平均全局效率，发现精神分裂患者具有较低的聚类系数和全局效率，但是精神分裂患者相对于正常被试特征路径长度更长，因此精神分裂患者脑网络节点的集团化程度较低，脑区之间的信息传输速率要低于正常被试者。

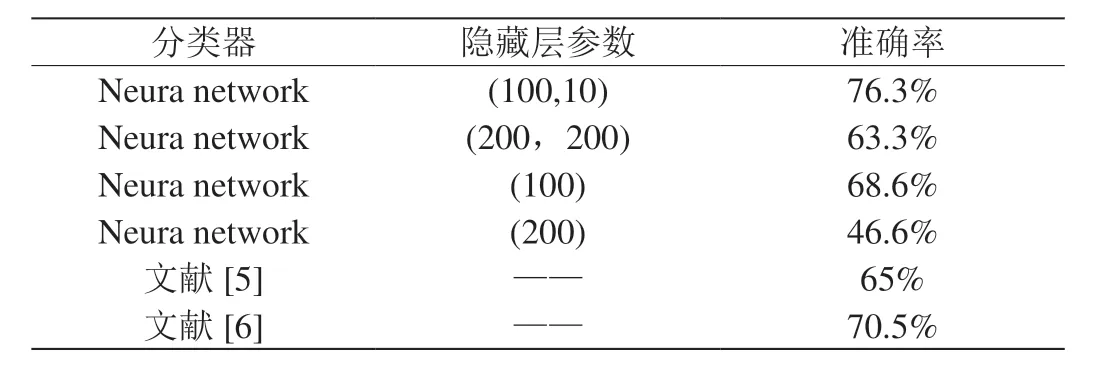
表1

3 总结

本文从数据分类的角度使用了一种基于神经网络的fMR图像分类方法，以精神分裂患者与正常被试的脑网络连接差异性作为分类特征本，并从差异性脑网络机制的角度去分析潜在患病机制。由于实验所提出的模型，其用于模型训练的体素都依赖于先验知识所划分的ROI区域，未充分考虑在全脑体素中，是否包含存在其他体素值影响分类的结果，因此下一步将深入了解临床医学、脑认知科学相关的专业知识，并与专业人员进行探讨，对fMRI数据中非ROI中体素运用到分类模型中，更深层次挖掘信息。