直升机挂架随动角速度对火箭弹发射角度的影响性
2020-06-12刘刚
刘刚
(中国直升机设计研究所 江西省景德镇市 333000)
航空火箭弹具有射程远、威力大、火力猛、成本低等优点,属于各型武装直升机火力系统的标配武器。对于集群目标,火箭弹主要用于提供瞬时密集火力,基于此项打击需求,在武装直升机火箭弹武器系统设计时必须考虑火箭弹的密集度,即火箭弹落在一定范围内。机载火控系统牵涉面广,涉及到各传感器精度、挂架随动、发射装置制造精度、火控解算精度等等,因此要严格控制各环节的技术指标才能达到武装直升机发射火箭弹杀伤敌方目标的要求。
机载挂架为火箭弹实时提供发射角度,挂架的角度精度、角速度等各项技术性能指标直接影响到火箭弹的发射角,从而影响火箭弹的作战效能。在挂架的各项性能指标中挂架随动角速度与火箭弹发射角度息息相关,机载火控通过模型解算赋予火箭弹一定射向、射角,挂架角速度的产生对火箭弹射角带来了初始扰动。因此,分析挂架随动角速度对火箭弹发射角的影响,具有实际工程意义。
1 机载武器系统工作流程
直升机载武器系统由火控计算机、平视显示器、光电系统、惯导、大气数据采集系统、挂架、发射装置等设备组成。光电系统搜索到目标获取目标参数(含方位、俯仰、距离等)给机载火控计算机。惯导、大气数据采集系统等获取载机空速、姿态、风向风速等数据。平视显示器用于飞行员对目标进行瞄准。挂架用于提供武器初始发射角。发射装置用于火箭弹点火及初始射向。
常用的机载无控武器轰炸原理主要分为连续计算投放点(CCRP,Continuously Computed Release Point)瞄准原理和连续计算命中点(CCIP,Continuously Computed Impact Point)瞄准原理。火控计算机根据载机飞行高度、空速、姿态角、火箭弹性能参数和风向风速等攻击条件,连续计算出如果当前投弹,该火箭弹在地面上的命中点的位置,以命中点标志符号在平视显示器上显示出来,飞行员操纵直升机将瞄准符号与目标重合,火控计算机算出初始射角,挂架将发射装置驱动到一定角度,发射装置发出点火信号,将火箭弹发动机工作将火箭弹发射出去。
从整个直升机发射火箭弹的工作流程可知,影响直升机发射火箭弹的散布的因素是火箭弹原有散布和机载武器系统产生。机载武器系统的误差源是平视显示器安装误差、惯导测量误差、大气数据采集系统测量误差、火控计算误差等。本文主要分析机载火控计算误差。
2 机载火控及外弹道原理
直升机发射的火箭弹是否能命中目标,取决于机载火控解算的发射角及离膛后的火箭弹外弹道。
2.1 机载火控原理
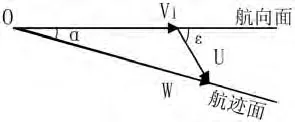
图1:空速、地速、风速矢量图

图2:瞄准图

图3:挂架运动对火箭弹施加的力
在航向坐标系中,直升机发射火箭弹瞬间载机、火箭弹、目标三者相互位置和运动关系见图1所示。无风时,载机相对地面固定目标的运动速度等于载机相对静止大气的运动速度,即载机的空速矢量V1。然而在真实环境中,风的变化是极其复杂的,为顺利建立火控模型,在空对地射击火力控制问题中,不考虑垂直风的影响,认为风速矢量始终在水平面内,垂直面内无风;且在武器射击范围内风速、风向无变化。风速矢量为U,载机相对地面固定目标的运动速度称为地速,地速矢量为W,则空速、地速、风速关系为:

在航向坐标系(OXYZ)H中建立载机、火箭弹、目标的相互位置和运动关系。载机空速矢量V1和XH轴向一致。载机火控计算机根据载机飞行高度H、空速V1、火箭弹的性能参数和风速U、风向角ε等攻击条件,连续计算出如果当前发射火箭弹,该火箭弹落在地面上的爆炸点的位置。在无风情况下,火箭弹落在M1点。在有风情况下,在投弹点O处用瞄准线瞄准目标M并发射火箭弹,经过火箭弹飞行时间T后,火箭弹命中M点。如果载机发射火箭弹后,仍然保持原有飞行状态不变,则载机会沿着OE方向运动,α为偏流角,为载机航向与载机航路的夹角。如图2所示。
在航向坐标系(OXYZ)H中,命中点M的位置为[1]:

式中,AXH为纵向射程,AYH为侧向射程,AZH为垂直射程,A0为火箭弹无风射程。
2.2 火箭弹运动方程
为了从原理上分析载机发射火箭弹的运动过程,有必要分析传统火箭弹运动模型。火箭弹在空中飞行状态,可简化为自由刚体质心的平面运动以及绕质心的转动所组成的合成运动。通常采用牛顿第二定律对火箭弹的质心运动进行研究,利用动量矩定理对火箭弹绕质心运动进行分析。由于火箭弹在飞行过程中,质量会发生改变,为了便于分析研究,将火箭弹重量视为定常物体。在火箭弹的主动段飞行过程中,在外力上加上发动机推力。
以火箭弹的质心位置为原点,火箭弹在弹道坐标系中的标量形式,运动方程组[2]如下:

火箭弹所受合外力F包括重力、推力、空气阻力、升力、马格努斯力、科式惯性力;Fx为切向力,改变v的大小,v为火箭弹速度;Fy为法向力,使速度在铅垂面上发生变化;Fz为横向力,使弹道偏转;ψ为侧向偏角;θ为高度倾角;m为火箭弹质量,当做定值。
3 问题分析与建议
通过调整火箭弹发射平台速度、火箭弹发射角度和发射平台与目标的相对高度,均可实现火箭弹对不同距离目标的打击。直升机作战高度与战场生存力息息相关,通过调整直升机的飞行状态达到瞄准目标效果显然不可取。为了提高火箭弹的发射包线,将载机上挂架设计成角度可调的状态,如此飞行员无需通过调整载机飞行状态同样可使瞄准圆瞄准目标,大大增加载机作战效能。
载机火控计算机根据目标相对载机的位置、载机速度、风速、风向等数据解算出发射角,挂架依据火控计算机发送的发射角将发射装置抬至某个角度。由于火控计算机一直在周期性的解算发射角,挂架的角度一直在变化,火箭弹点火后离膛时,挂架随动时的角运动易给火箭弹发射角产生初始扰动。文中2.1节机载火控原理的瞄准方程与2.2节火箭弹动力学运动方程组中并未考虑挂架随动状态下对火箭弹的强扰动是否会产生载机对目标的瞄准偏差和火箭弹弹道偏差。如若会产生影响,则直接影响载机的作战效能。
挂架运动时对火箭弹施加的力如图3所示。当挂架向上俯仰运动时,火箭弹所受的力F架垂直Fx向上;当挂架向下俯仰运动时,火箭弹所受的力F架垂直Fx向下。当挂架不随动时,火箭弹的运动方程如式(3)所示。当挂架随动并对火箭弹运动轨迹有强扰动时,需考虑挂架随动对火箭弹发射角的影响。扰动影响方程如下:

其中,β为挂架随动时对火箭弹产生的扰动角,即合速度与v的夹角;v架为发射装置前端的线速度;ω为挂架角速度,向上俯仰为正,向下俯仰为负;r为转动半径,即挂架转轴到发射装置前端的距离。
假设火控计算机解算的火箭弹的发射角为γ=3度,挂架随动状态。若挂架角速度ω=90°/s,转动半径r=1m,火箭弹出膛速度v=180m/s,则计算可得β=0.5°。表明在火箭弹离膛时刻挂架的角速度ω=90°/s时,火箭弹离膛后发射初始角度会比火控计算机解算的发射角γ多0.5度。通过实验可知发射角存在0.5度偏差的情况会造成火箭弹命中精度偏差大。
为了降低挂架随动角速度对火箭弹散布的影响可从三方面开展工作:
(1)火箭弹设计厂家考虑挂架随动角速度对火箭弹弹道的影响,在火箭弹运动数学模型中增加挂架随动角速度变量;
(2)机载火控算法设计时考虑挂架随动角速度对火箭弹命中点的影响,在火箭弹瞄准方程中增加挂架随动角速度变量;
(3)依据火箭弹发射角精度设计挂架随动角速度值,即使挂架随动角速度引起的火箭弹扰动角小于火箭弹发射角精度值。考虑工作难度及工程实现,本文建议采用通过控制挂架随动角速度设计值的方案降低挂架随动角速度对火箭弹发射角的影响。
4 结论
本文通过对武装直升机火箭弹发射流程的分析,发现机载挂架随动角速度会影响火箭弹发射角,从而影响火箭弹的散布。追根溯源,本文分析了直升机火箭弹瞄准轰炸原理和火箭弹运动学方程数学模型,发现机载火控及火箭弹运动方程并未考虑挂架随动角速度对发射角的影响。
最后本文对发射火箭弹时机载挂架随动角速度对火箭弹发射角度的影响机理进行分析,当挂架运动角速度在一定范围内时,挂架的运动不足以对火箭弹命中精度造成影响,同时给出减小此种影响的合理建议。
