基于传递矩阵法的夹心式换能器固有频率分析

邓 韬，卢钰仁

(1.国电科学技术研究院有限公司成都分公司，四川成都 610000；2.北京理工大学机械与车辆学院，北京 100081)

0 引言

随着功率超声应用的发展，夹心式纵向振动换能器也逐渐得到广泛应用，相比之前的电磁超声换能器[1]来说，其以功率大、振动方式单一、结构设计成熟等优点，在超声波清洗、超声波焊接、超声波消除残余应力等方面具有巨大优势。本文讨论的压电陶瓷是PZT-8。这种换能器主要在纵向振动模式的基频值上工作，通常在12～40 kHz之间，其功率一般高达1 kW甚至更高。电声转换效率在基频值处最高，因此确定基频值具有重要意义。但由于换能器材料种类多、结构复杂，实际基频与理论频率不一致，影响了效率。因此，迫切需要解决如何保证换能器的转换效率接近实际固有频率的问题。

夹心式换能器的结构参数是基于半波长设计理论，它通过边界位移和应力的连续性来适应频率，但不能从理论上加以验证。目前，有限元法可以用来计算不同振型的频率。文献[2]可以得到与纵向振动模式对应的频率。然而，计算过程复杂，需要较高的计算机性能。

通过对振动力学理论的改进，传递矩阵法成为分析物理结构系统固有特性的一种简单快捷的方法[3-4]。它在振动机械技术领域得到了广泛的应用，具有简化不同振型的矩阵、降低计算成本等优点。本文采用传递矩阵法对夹心式纵向振动换能器的固有频率进行了分析，并与半波长设计法、有限元法和实验法的结果进行了比较。

1 等价和离散化

换能器是一个结构复杂的连续弹性体，夹心式纵向振动换能器结构如图1所示，传递矩阵法主要研究集中质量的多自由度组合系统。因此，在采用传递矩阵法对换能器进行分析之前，必须进行结构等效和系统离散化。

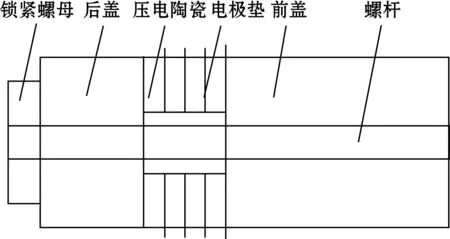
图1 夹心式纵向振动换能器原理图

结构等效是指同一段的两部分或多部分结构等效于一个结构[5]，等效结构的材料属性参数可按下式计算：

(1)

(2)

式中：E*为等效弹性模量；ρ*为等效密度；s为横截面积。

此外，由于电极垫等小结构对系统的影响很小，因此省略了这些小结构。夹层式换能器的等效模型如图2所示。

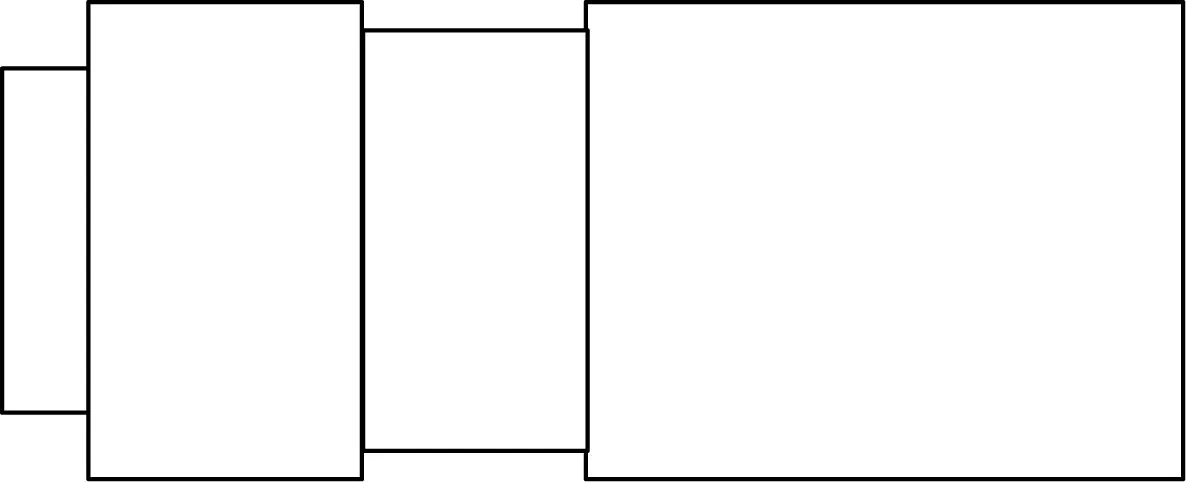
图2 夹心式换能器的等效模型

换能器系统的离散性主要是系统质量的集中，因为所关注的振动模式是纵向振动。质量离散化是将连续分布弹性系统转化为集中质量多自由度系统。例如，弹性系统的阶梯轴(图3)可离散成集中质量块和无质量弹簧段组成的多自由度系统(图4)，这意味着它将系统质量集中在多个节点上，并且通常在系统突变的部分(例如不同的部分和材料)处选择节点位置。质量密度的原理是质心的初始位置不变，系统的总质量也不变[6-8]。

图3 阶梯轴示意图

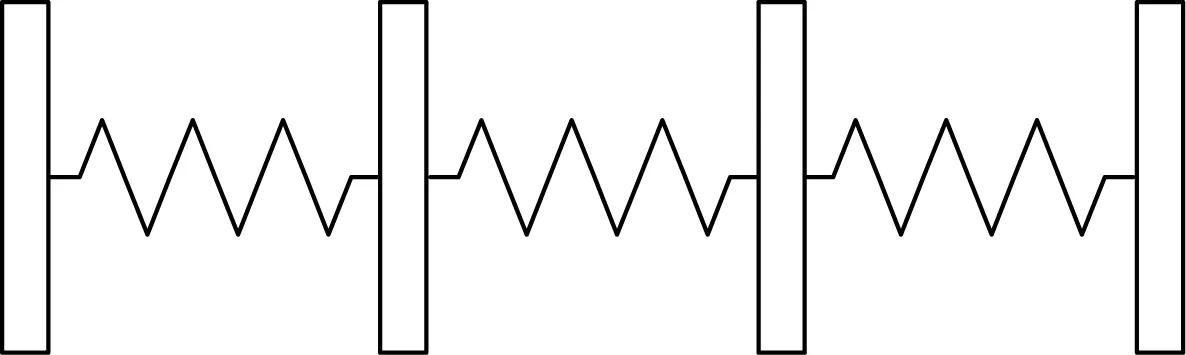
图4 阶梯轴离散系统

2 换能器模型的建立

多自由度系统可以看作是质量集中块和无质量弹簧段的多个组合，它们依次连接。组件如图5所示。通过弹簧和质量等效分析，可以得到各构件的传递矩阵。

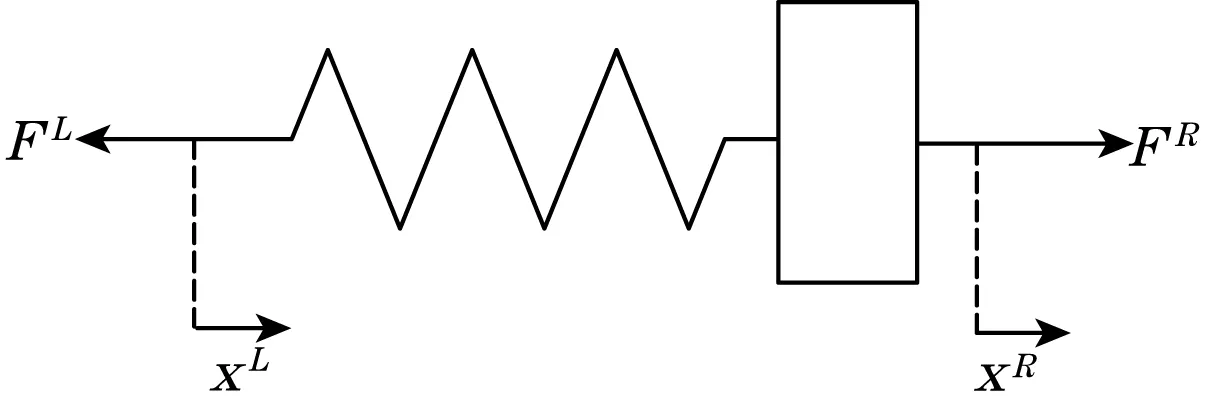
图5 质量集中块和无质量弹簧截面的组成

2.1 无质量弹簧截面传递矩阵

k为弹簧刚度，分析第i个部件的弹簧截面ki，如图6所示。

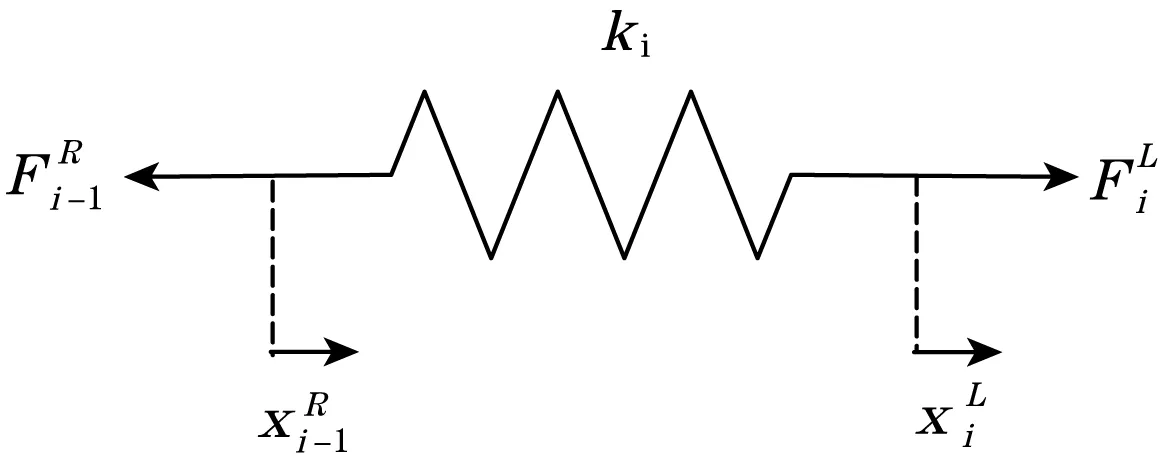
图6 弹簧截面模型

状态可以用位移和力来表示。由于弹簧截面仅为一维自由度，因此只考虑轴向位移x和力F的连续性。设左、右状态矩阵为：

(3)

(4)

当节点位置改变时，两端的力相等。那就是：

(5)

(6)

左右两端的关系为

(7)

cri表示弹簧截面ki两端的矩阵传递系数，即：

(8)

k通过以下等效公式得出：

(9)

式中：L为长度;E为弹性模量。

2.2 质量集中块传递矩阵

如图7所示，分析了第i部分的质量集中区mi。

图7 质量集中块模型

设左、右状态矩阵为：

(10)

(11)

根据牛顿第二运动定律，存在：

(12)

(13)

式中ω为角频率。

左端和右端之间的关系如下：

(14)

czi表示质量mi两端的矩阵传递系数，即：

(15)

2.3 构件传递矩阵

将无质量弹簧截面的传递矩阵与质量集中块相结合，得到构件的传递矩阵。根据式(7)和式(14)，得到第i-1部分与i部分的转移关系为

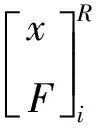
(16)

ci表示组件的矩阵转移系数，且：

(17)

3 夹心式换能器固有频率的求解

以图2所示换能器的等效结构为例，分析了夹层式纵向振动换能器的固有频率。考虑质量集中原理，将等效模型离散为由4个组件组成的多自由度系统，以不同横截面积的位置为节点，如图8所示。离散化后换能器的具体参数值见表1。

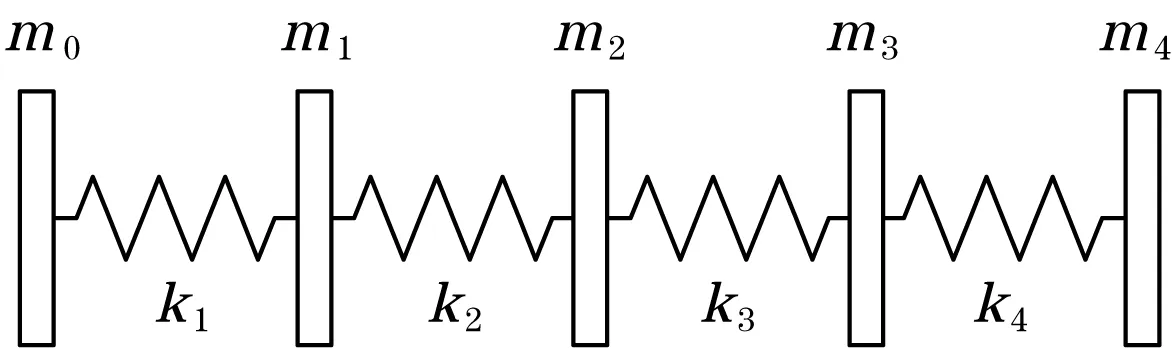
图8 夹心式换能器的多自由度系统模型

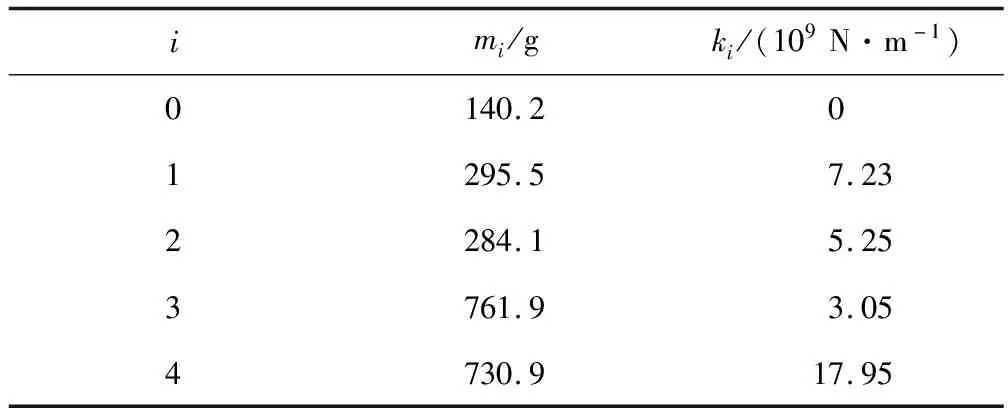
表1 各部分参数

根据式(16)，系统左右端之间的关系为

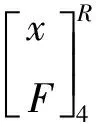
(18)

C表示系统的总传递系数，即：

(19)

其中，c11、c12、c21和c22仅与角频率ω有关。边界固定在左侧，自由端在右侧。

x0=0

(20)

F4=0

(21)

则式(18)变为：

(22)

转换后得到约束条件：

c22(ω)=0

(23)

本文设计了MATLAB程序，用于计算换能器的固有频率。用公式f=ω/2π求得f=15.37 kHz。

4 有限元模拟与实验验证

4.1 有限元模拟

利用有限元分析软件ANSYS建立了换能器的三维模型，并对其进行了网格化。有限元模型如图9所示。换能器材料性能参数见表2。

图9 换能器的有限元模型

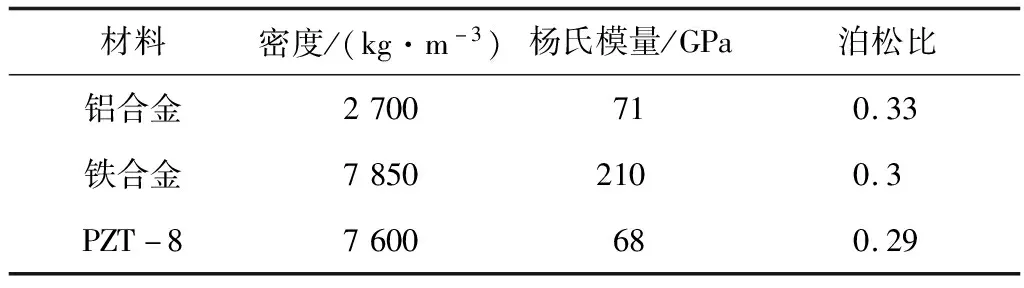
表2 材料性能参数

利用ANSYS模态分析模块对换能器进行模态仿真，得到纵向振动模态的固有频率f=14.89 kHz，其相应形式如图10所示。

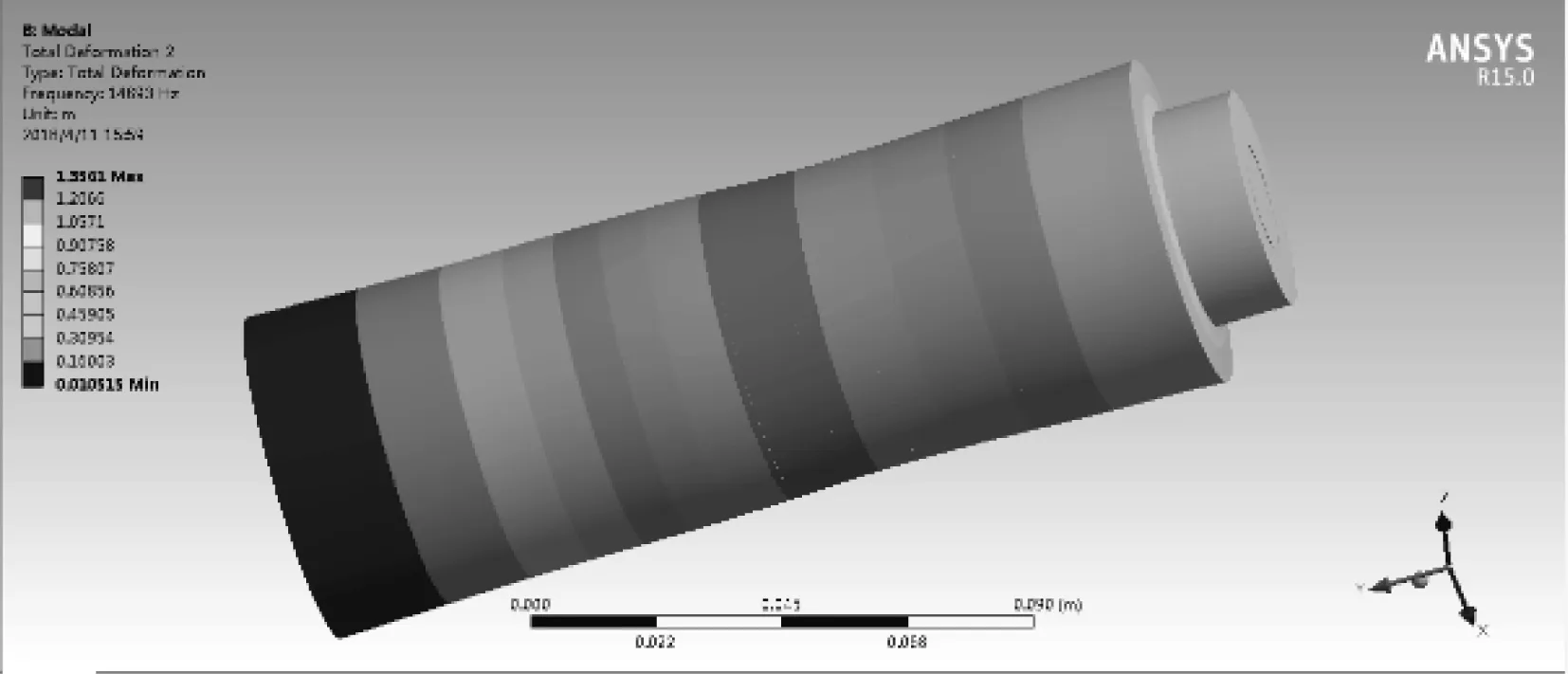
图10 换能器的纵向振动模型

4.2 实验验证

建立了实验测量系统，用激光测振仪采集换能器的表面振动信息，如图11所示。用脉冲激励法分析了换能器的固有频率。

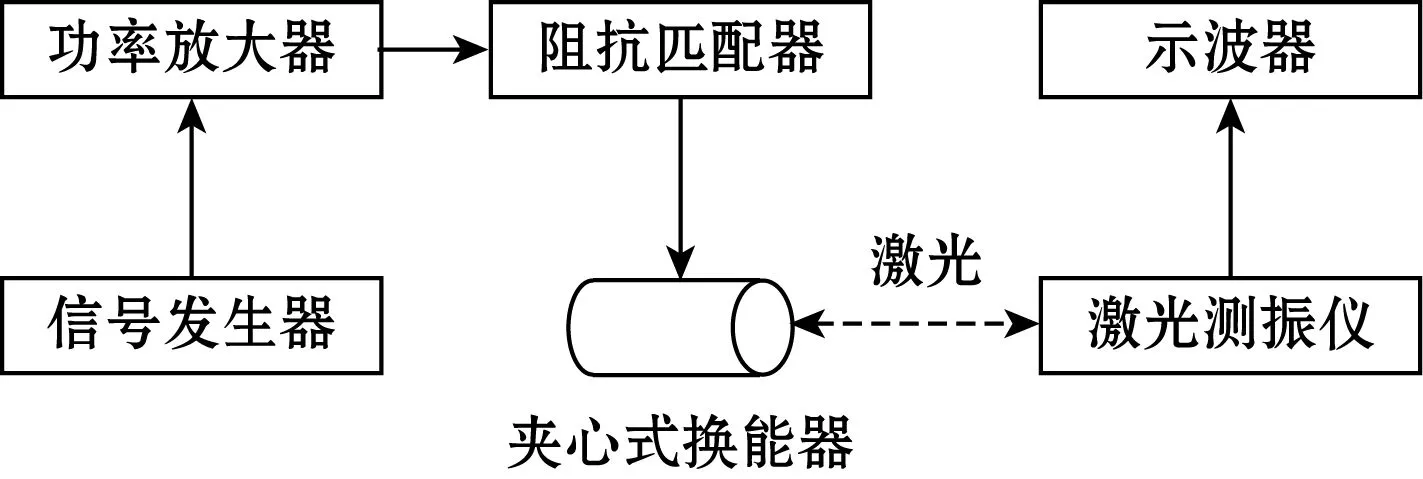
图11 实验仪器连接图

信号发生器输出脉冲信号，如图12所示。经功率放大器放大后，信号激励换能器振动，然后用示波器记录激光振动计的模拟波形，如图13所示。然后进行波形的频谱分析。结果表明，固有频率值为15.15 kHz，如图14所示。

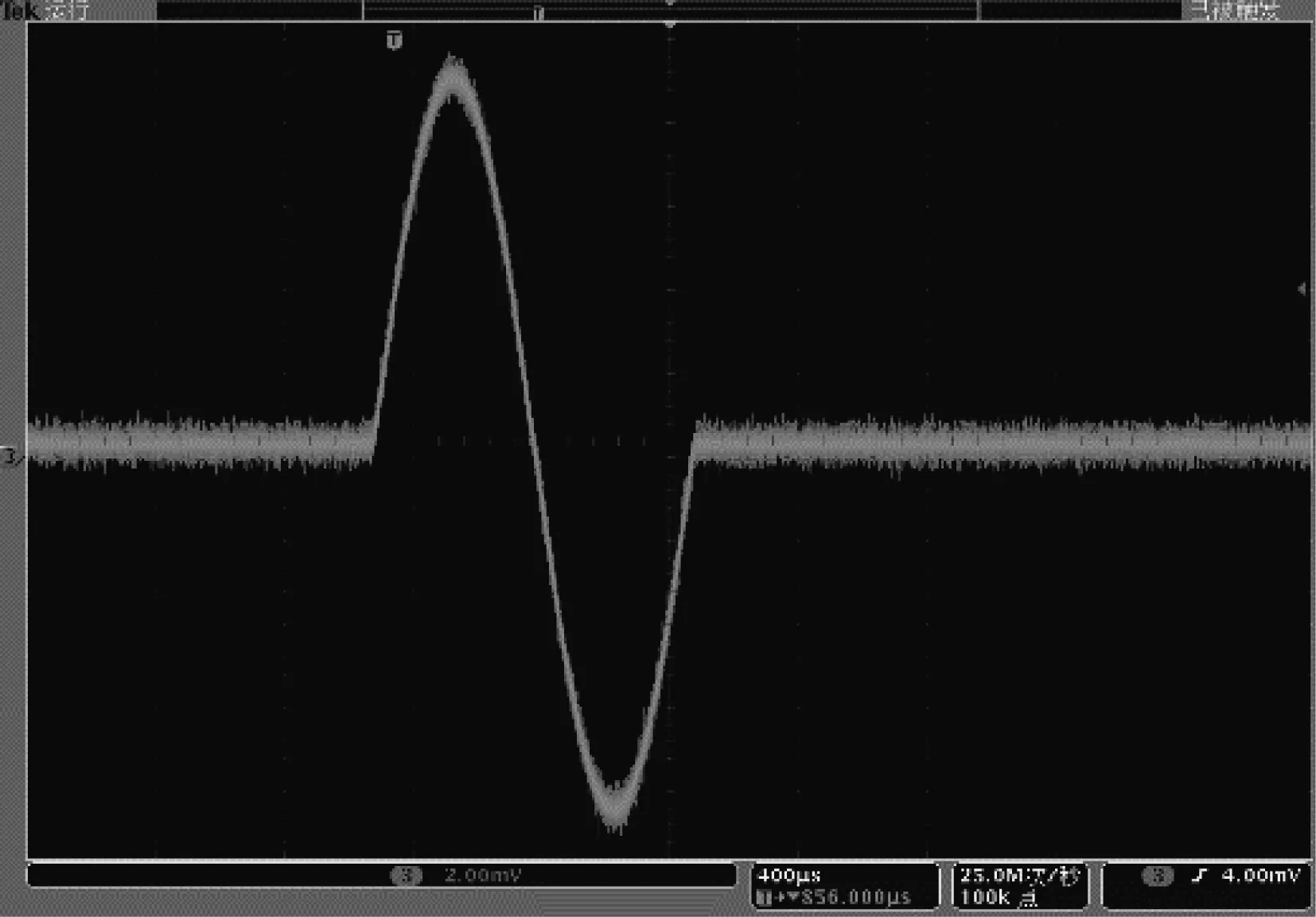
图12 脉冲激励信号

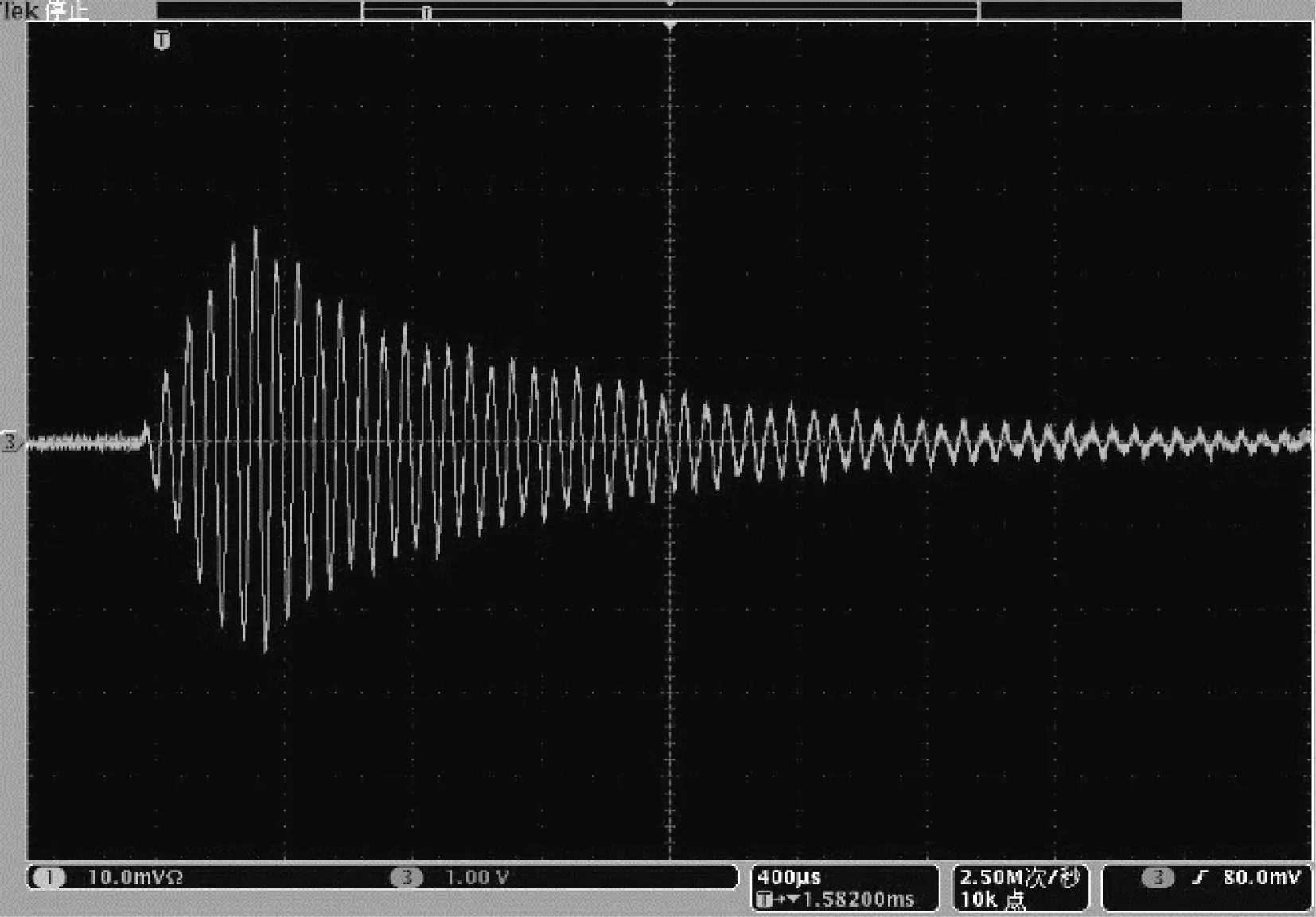
图13 振动模拟信号

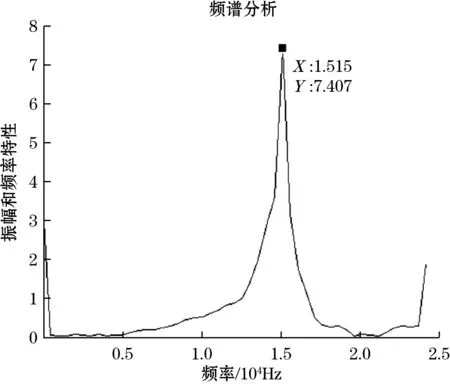
图14 振动信号频谱图

4.3 结果讨论

采用传递矩阵法、有限元法和实验法分别得到了同一夹心式换能器的固有频率。根据半波长理论设计，所讨论的夹心式换能器的理论固有频率为15.30 kHz。

首先，将传递矩阵法和有限元法的结果与半波长理论方法的理论值进行比较，如表3所示。

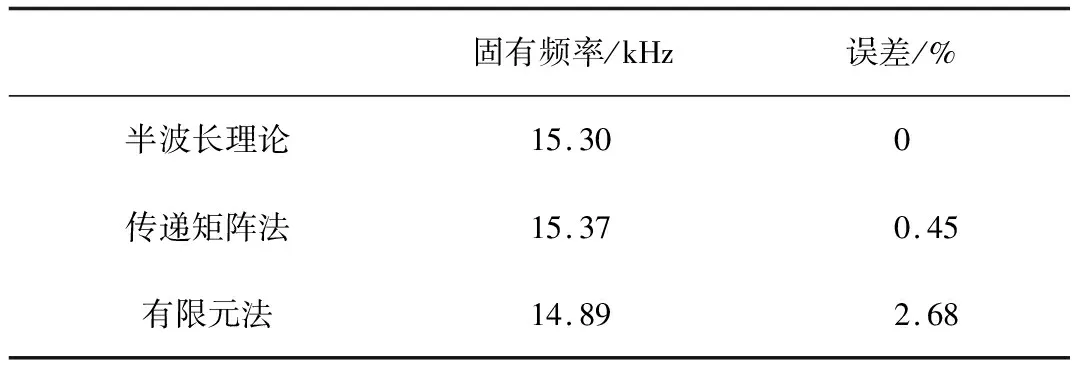
表3 结果与理论值比较

由表3可以看出，传递矩阵法计算的固有频率与理论值非常接近。其误差仅为0.45%，有限元法的误差为2.68%。传递矩阵法更精确，其等效模型易于建立，而且计算量很小。

然后将传递矩阵法和有限元法的结果与实验方法的实际值进行比较，如表4所示。

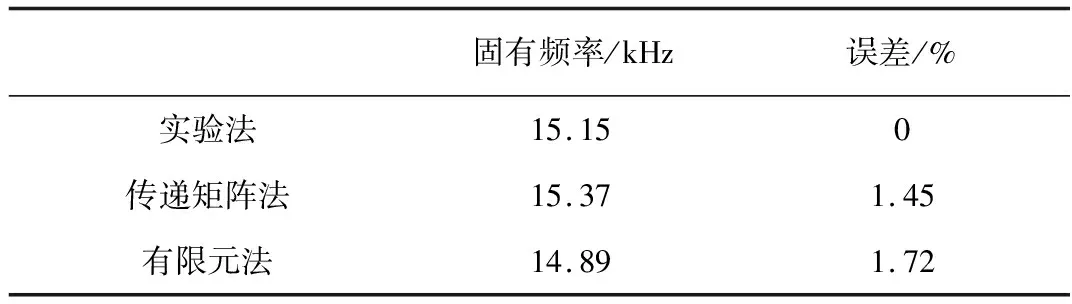
表4 结果与实验值比较

从表4可以看出，传递矩阵法和有限元法结果的误差分别为1.45%和1.72%，与实验方法得到的实际固有频率相比，两者误差均在允许范围内。结果表明，采用传递矩阵法计算夹层式换能器的固有频率是可行的，分析结果可用于验证夹心式换能器的设计。

5 结束语

本文以夹心式换能器为研究对象，对其固有频率分析方法进行了研究。基于多自由度系统模型，建立了传递矩阵法。首先，根据质心不变的原理，对连续弹性体进行平衡和离散化。推导和讨论了无质量弹簧截面和质量集中块的单元矩阵。然后对离散化的多自由度系统模型进行整体分析。结合边界条件获得换能器分析结果，其比有限元法更接近理论值。

另外，与通过脉冲激励方法获得的实验值相比，传递矩阵法和有限元法两者的误差大致相同，并且在允许的误差范围内。

但是，与有限元法相比，传递矩阵法在构造等效模型、降低计算成本、降低计算机软硬件需求等方面具有更大的优势。因此，传递矩阵法是分析夹心式换能器固有频率的一种较有效的方法。