基于地理加权回归的东北地区降水量空间栅格化研究

蔡学博

(辽宁省康平县自然资源保护与行政执法中心，辽宁 康平 110500)

降水是生态系统中的重要组成部分之一，研究区域降水量空间分布对衡量区域生态系统健康、优化国土资源开发具有重要意义然而降水观测采用测站式点位注记，受制于测站离散分布影响，并不能完整反映空间信息，因此将站点数据进行栅格化处理是水资源管理、气候变化研究的重要内容[1-2]。地理加权回归模型(GWR)是面向地学因素并基于空间位置的非均匀插值方法，目前已经在土壤空间变异、水质评价等方面得到广泛应用，然而在气象数据栅格化的研究方面尚待挖掘[3-4]。

1 研究区域

东北地区(黑龙江、吉林、辽宁省全省及内蒙古东部)位于中国大陆最北、最东端，西接蒙古、北望俄罗斯、东滨朝鲜半岛，属于依山傍海挺近内陆之地，地理坐标为E115°33'35″-134°58'28E，N38°43'15″-53°33'35″N，面积达133.441万km2。区域主要是温带季风、温带大陆性气候，全年四季分明、雨热同期、冬季漫长，积温从南向北减少，依次分属中温带、寒温带，年平均气温在-1.3-10.5℃之间，降水量为250-1000m，跨立湿润区至干旱区。主要地形有大兴安岭、小兴安岭、长白山、内蒙古高原、东北平原，发育有黑龙江、鸭绿江、辽河、图们江、乌苏里江等水系。该地区以以汉民族为主，聚居的满、蒙、朝鲜等少数民族。全区地理位置如图1所示。

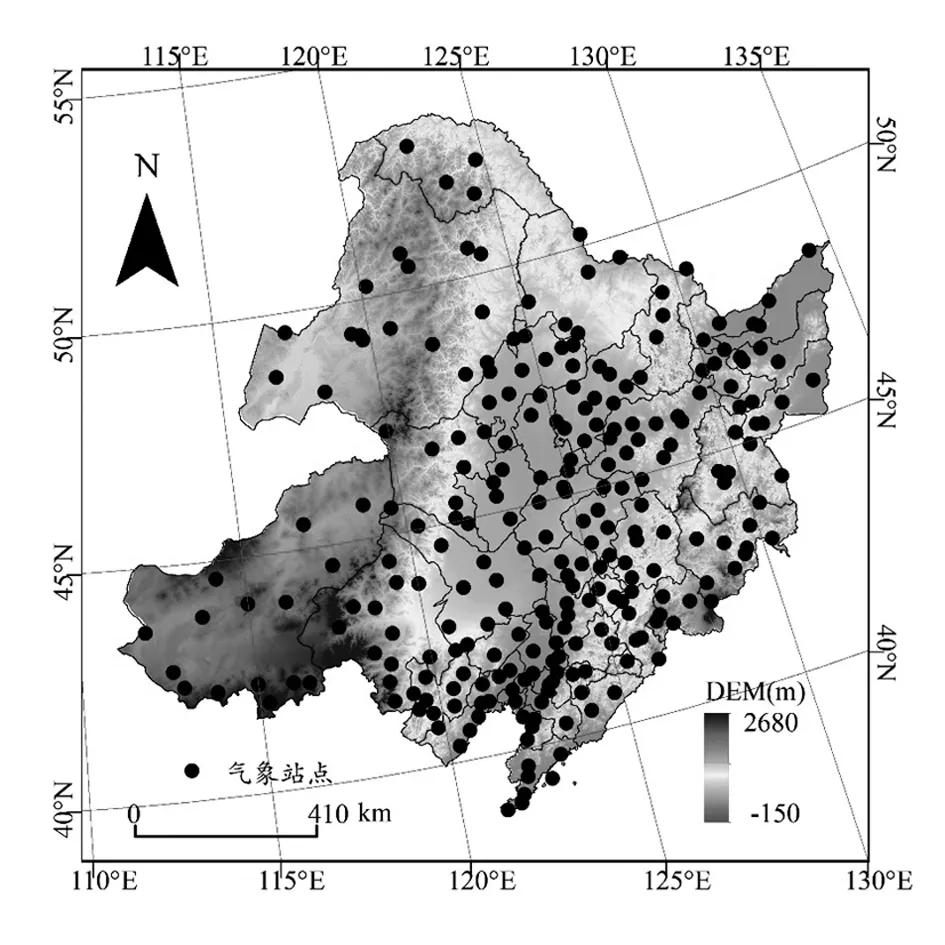
图1 东北地区地形图与气象站点分布

2 研究方法

2.1 地理加权回归

地理加权回归(geographically weighted regression,GWR)模型基于普通最小二乘法原理的一种面向地理空间的建模方法，其特点在于将空间位置嵌入回归参数中，使得参数可进行局部估计，即建立多个局部空间普通最小二乘模型。原理如下：

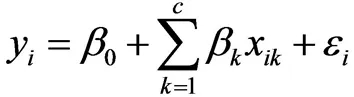
(1)

(2)

式中：i=1,2,2……n，表示测点数量；k=1,2,3……K，表示解释变量个数；xik表示第i个测点处第k个变量的观测值；期开奖坐标表示为(ui,vi)；β0为回归模型的常数项；第k个变量的回归系数为βk；εi为误差项。模型系数采用空间点位矩阵表示：

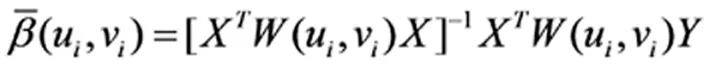
(3)

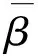
2.2 数据资料

研究中使用的气象数据来源于中国气象科学数据共享服务网站(http://data.cma.cn/site/index.html)。该数据由中国气象局整编了全国756个气象站点，由于站点检测起始时间不一致，部分站点数据存在较多遗漏，故而以研究时域为1990-2010年。研究区境内的站点有254个如图1所示。其中数据内容为降水总量，时间分辨率上属于均年两种尺度。各站点均无遗漏，质量可靠。

2.2.1 东北地区气象站点降水量观测值统计特征

东北地区254个气象站点多年平均降水量相差较大，其中二连浩特站降水量最低，仅为144.3mm，宽甸站降水量最丰富，达1098.2mm，最大差值为953.9mm，平均值为546.6mm。图2为全部站点降水量分布直方图，统计显示有3个测站降水量少于200mm，介于200-300mm的达8个，在300-400之间的有27个，59个测站降水量介于400-500mm，75个测站在500-600mm，降水量介于600-700mm的有46个，介于 700-800mm的达21个，10个测站降水量在800-900mm，3个测站降水量达 900-1000mm，2个测站降水量超过1000mm。

2.2.2 东北地区降水量与环境因子关系

选取能够反映降水空间依赖性的环境因子是建立GWR降水量预测模型关键。参照前人研究经验，选取经度、纬度和DEM作为解释因子能够描述降水量空间分布的地带性规律。为证明上述3个因子的有效性，利用空间提取至点的方法，提取了254气象站的点位、DEM信息，并利用线性回归分析研究二者关系(图3)。图3-a显示，区域降水量呈正相关关系，R2达0.253，在0.05水平上达到统计显著性，表明该地降水量随着经度增加而增大。图3-b显示降水量与纬度的相关性系数平方纬0.13，说明随着纬度升高，降水量逐渐减少。前述表明表明了区域降雨量具有显著的全局分布规律，而图3-c显示了降水量与DEM的相关性不明显，这意味着在地形因子并不影响全局降水量分布，而在局部起作用。GWR模型不仅考虑了降水量分布的经向、纬向地带性全局规律，更在于解决地形引起的局部变异性，因而选取这3个因子作为降水量分布的解释变量具有一定效用。

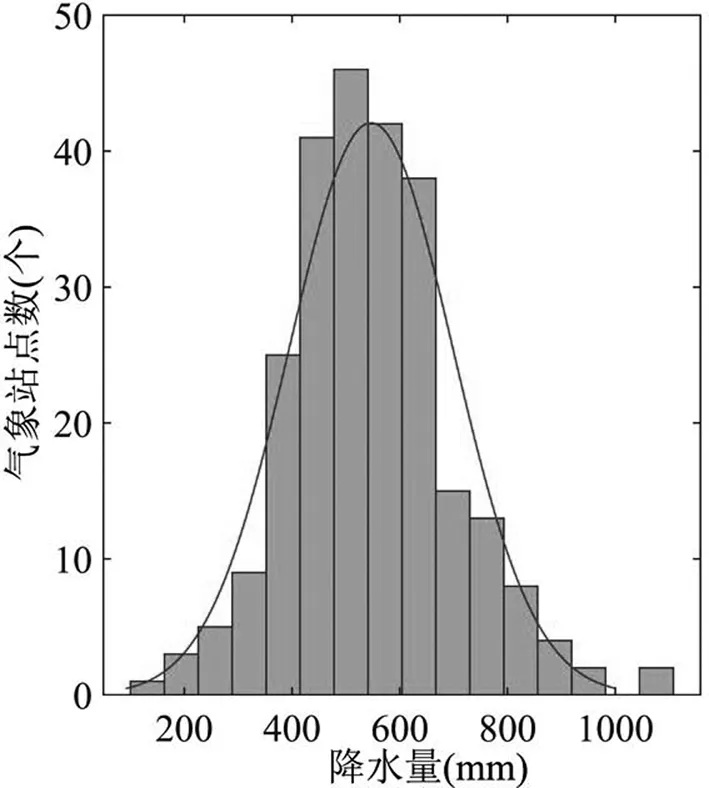
图2 东北地区254个气象站点降水量分布直方图

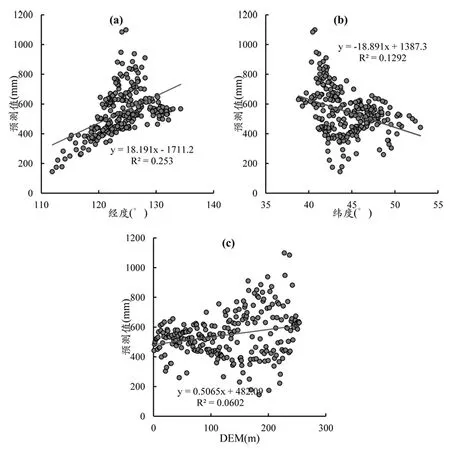
图3 东北地区降水量与环境因子相关性

2.3 东北地区降水量空间自相关性

空间自相关性检验是建立GWR降水量空间分布模型的前提。GWR模型正是利用区域化变量在邻近位置处的相关性对其他未知空间进行估计。利用全部样本站点的经纬度坐标与降水量信息计算空间邻近距离，进而求得不同距离处的半方差值。结果显示，其半方差离散点符合高斯模型分布，表达式为：669.78*Nugget+27058*Stable(578400,1.8119)。由此可知，其块金结构为669.78/27058=2.48%，其值小于25%，说明其具有强烈空间自相关性，因此可适用GWR模型。因而运用SAM4.0软件构建东北地区降水量空间模拟GWR模型(图4)。

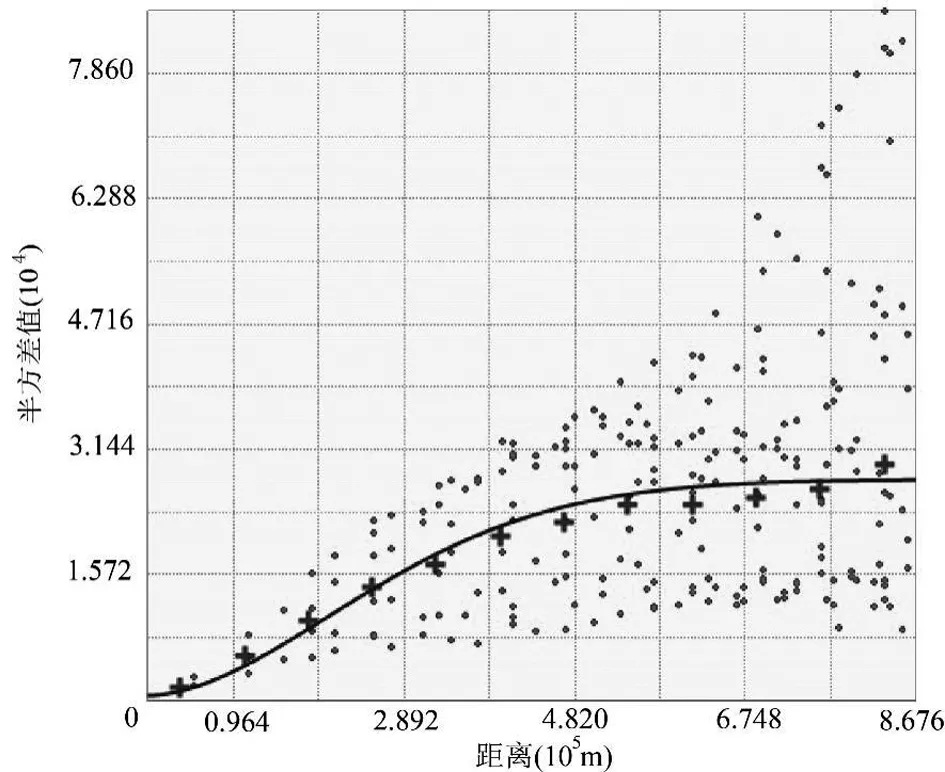
图4 东北地区降水量分布半方差结构

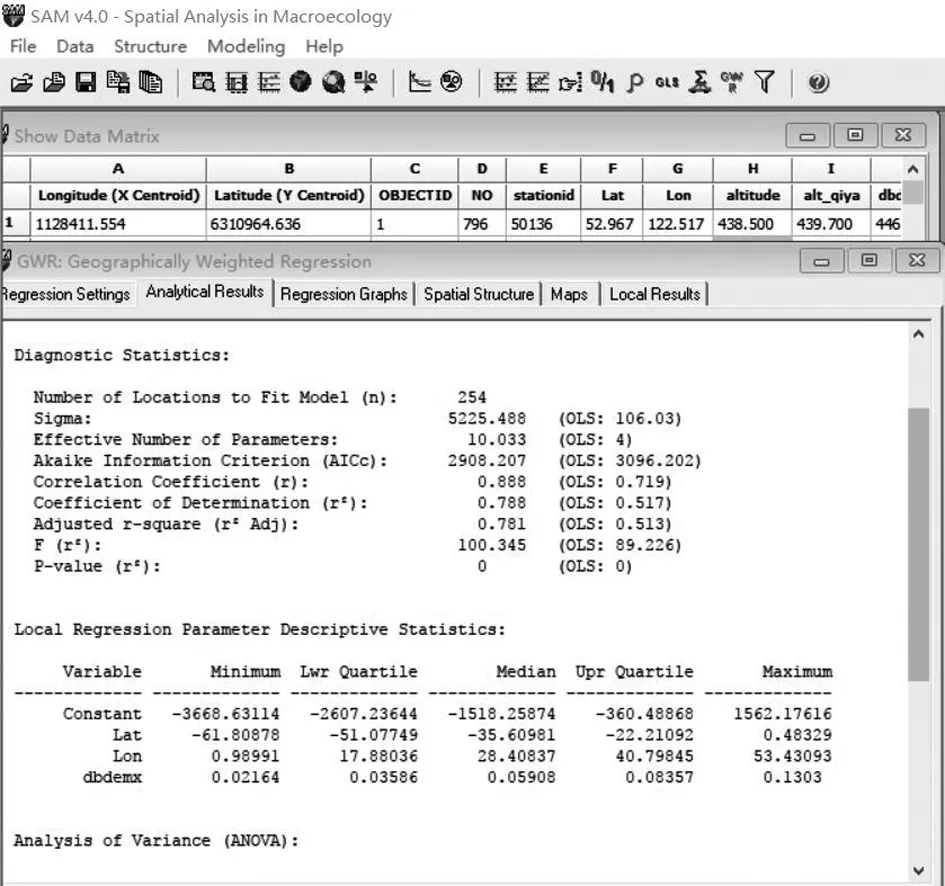
图5 SAM软件操作界面与结果

2.4 东北地区降水量空间分布

图5-a为基于GWR模型得到的东北地区降水量空间分布图。位图显示区域降水量介于138-1094mm之间，平均值为490.5mm，变异系数达26.56%。降水量分布呈现自动向西减少、自北向南增加格局，这与海陆位置、降雨水汽来源行进路径密切耦合。丰水区位于东南部辽东丘陵、长白山东麓，该地为迎风坡，距离海洋位置近，海洋水汽易于到达，受地形抬升成云致雨。缺水区位于科尔沁沙地、内蒙古高原地区，局部降水量少于400mm。

为证明GWR模型的有效性，将本研究结果与Wang[5]等人的研究结果进行对比。后者采用Anusplin插值技术，以DEM数据为基础得到了区域降水量1km分辨率的位图(图5-b)。结果显示降水量值域范围为142-1103mm，平均值为493.2mm，变异系数达36.24%。

对比分析可知，本研究与Wang[5]的研究对该地降水量空间模拟值域相近，并且具有相似的分布特征。但后者能反映更多的局部细节信息，而本研究则对微域特征进行了概化，这是由于变量选择、插值方法、样本数量不同导致的。Wang的研究中，样本量比本研究更丰富，这确保了对局部降水量模拟的准确性；同时其采用的Anusplin插值方法属于面向气象要素的专业技术，这与GTWR模型原理存在一定差异；此外，其仅以DEM为辅助变量，因此获得的降水量分布图班更加破碎、细致，而本研究还加入了经纬度信息，这类变量促进了空间分布信息的模糊化。

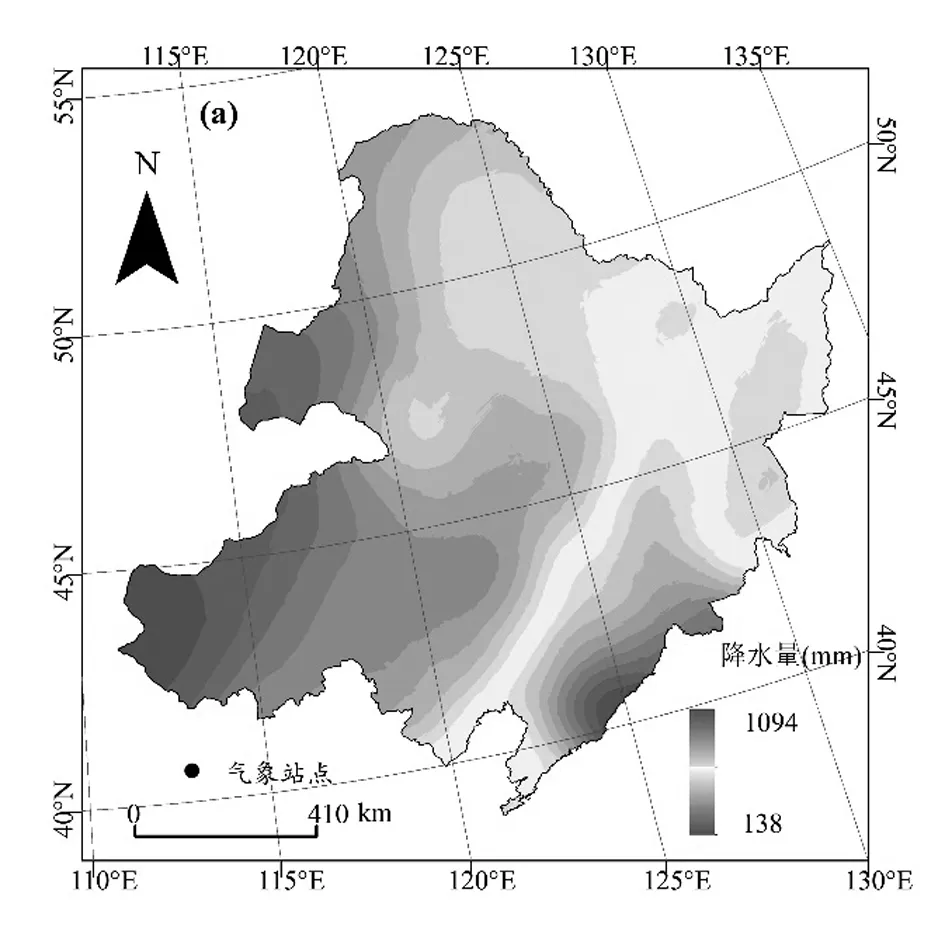
图6-a 东北地区降水量空间分布

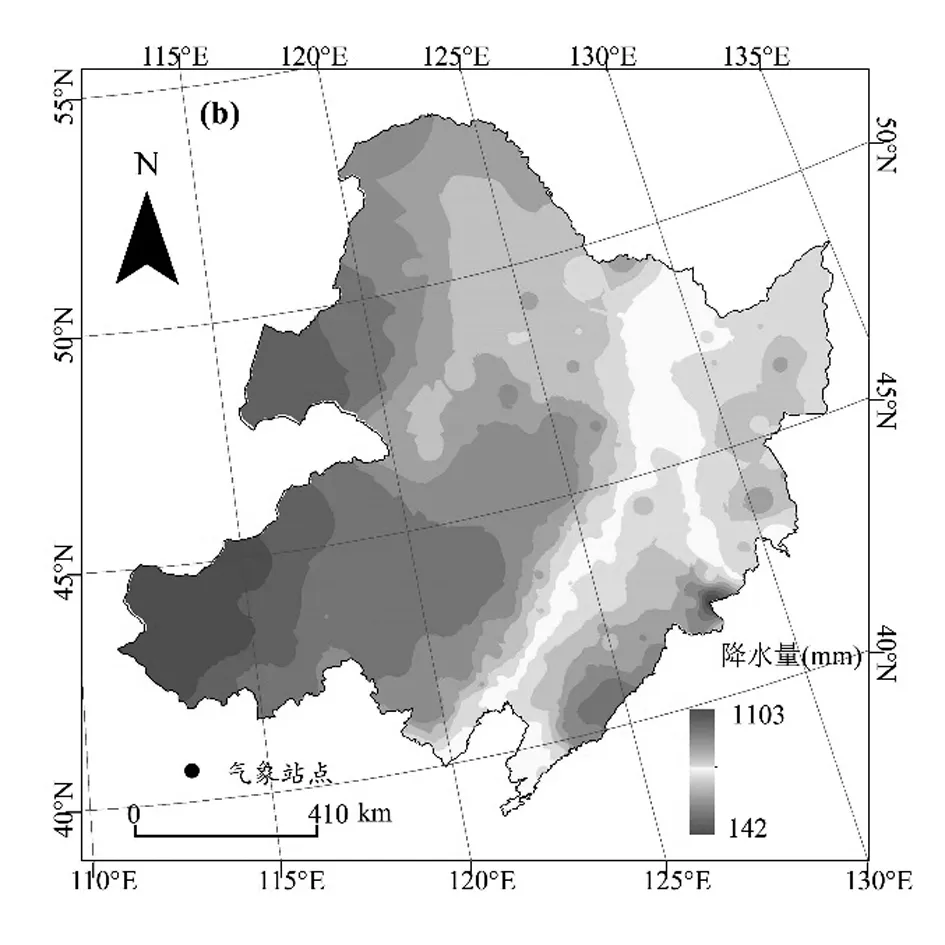
图6-b 东北地区降水量空间分布

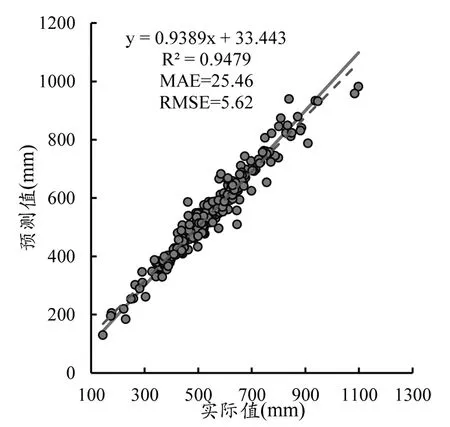
图7 东北地区254个气象站点降水量预测值与实际值

2.5 GWR模型精度分析

图6为254个气象站点降水量实测值与模拟值的拟合关系，可知二者离散度较小，说明总体误差不大。统计显示，其误差介于-136mm(珲春站)-124mm(逊克站)，其平均值为0.1mm，误差统计符合正太分布。分析表明，实测值与模拟值之间具有较高的一致性，其相关系数平方达到0.95，平均绝对误差MAE为25.46mm，均方根误差RMSE仅为5.62mm。与石志华等人的研究相比，本研究中GWR模型精度更高，误差值在可接受范围内，表明该方法具有一定可行性。

3 结 论

基于有限离散气象站点资料，以经纬度和DEM为辅助变量，构建东北地区降水量空间分布GWR模型，实现降水资料空间栅格化。东北地区地形广袤、分异明显，降水量具有从沿海向内陆减少格局，GWR模型不仅纳入空间位置信息还加入地形效应影响，较为准确反映区域降水量分布特征。但与专业的Anusplin插值技术相比，GWR模型在描述降水量空间分布的局部信息方面有待改进。