水力耦合裂隙岩体变形破坏机制研究进展

张 英,李 鹏,郭奇峰,蔡美峰,任奋华,武 旭

(1.北京科技大学 土木与资源工程学院，北京 100083； 2.金属矿山高效开采与安全教育部重点实验室(北京科技大学),北京 100083; 3.北京市市政工程研究院，北京 100037)

地下岩体经过漫长的地质构造作用下产生微裂纹、孔隙、节理和裂隙等各种各样的缺陷，地下水在孔隙和裂隙中发生运移，并且以孔隙压力(渗透应力)的形式作用于岩体，影响岩体中应力场的分布，同时岩体应力场的改变促使裂隙产生变形、扩展、剪切滑移以及贯通，进而影响裂隙的渗透性能，这种相互作用、相互影响的现象称为水力耦合或渗流-应力耦合，在地球科学和力学中称为水-岩(土)耦合和流-固耦合[1-3].目前针对水力耦合研究主要体现在：一方面，假设岩体内部孔隙、裂隙结构系统不发生改变(即岩体不发生损伤破裂或发生的变形可忽略不计)，仅考虑粗糙度、隙宽等因素研究岩体内部孔隙、裂隙结构系统的渗流特性；另一方面，在实际工程中，工程扰动作用会不可避免地造成岩体内部结构的损伤和破裂，要考虑裂隙岩体变形破坏过程中损伤对岩体力学性能劣化及渗透性能产生的影响[4].大量的岩体工程实践表明，工程扰动诱发的岩体损伤变形与破裂行为及其造成岩体中渗流场的改变是导致大规模岩体工程失稳和工程地质灾害的主要原因之一[5-6].

直至20世纪60年代，对于裂隙岩体渗流-变形-破坏机制的认知尚不清楚，造成很多重大地下工程事故的发生[7-9]，如：1959年12月法国Malpasset双曲拱坝在渗透压的作用下使坝肩岩体沿下游断层滑移，最终导致溃坝事故，如图1所示.1963年9月意大利Vajont大坝由于水位的升高，库岸边坡坡脚处受到较大的挤压力，引起滑坡，造成重大的生命和财产损失.1954年12月唐山林西矿在开采过程中，高水头压力石灰水通过断层进入矿井，引发突水灾害.1962年11月中国梅山连拱坝在渗透压力的作用下在右坝肩上出现裂缝，致使大坝岩体发生明显位移.

21世纪随着岩土工程的蓬勃发展，愈来愈多的岩土工程因水力耦合的问题造成施工技术难度增加，大坝失稳垮塌、边坡滑坡、隧道施工过程中的岩溶塌陷涌水、采矿活动中的突水、淹井等工程失稳破坏问题加剧[10].据国家统计局统计中国近十年地质灾害数可知(见表1)，每年发生的地质灾害中滑坡灾害起数所占比例最大，在50%以上.此外，90%以上的岩体边坡破坏和地下水渗透有关[11]，90%以上的煤矿突水事故与岩层水渗透有关[12]，30%～40%的水电工程大坝失事是由渗透作用引起的[11].因此，需要学者们对水力耦合问题进行长期深入研究.

图1 Malpasset拱坝失事原因[9]

水力耦合研究涉及岩体力学、水力学、材料学等多学科的交叉，是应用基础科学研究发展中的前沿性课题和亟待解决的工程技术问题.如图2所示，裂隙岩体中饱水的孔隙或裂隙由于外部载荷的变化或内部孔隙流体压力的变化而发生变形，其变形过程十分复杂，因此亟需弄清水力耦合机制.本文针对裂隙岩体(饱水)水力耦合问题，通过搜集并整理国内外研究成果，从水力耦合作用下完整岩体和裂隙岩体的力学特性、渗流特性、变形破坏机制以及数值模拟研究等方面进行系统的归纳和分析，指出了水力耦合研究目前存在的问题，给出了指导性意见与方法，并对未来水力耦合研究的发展趋势进行了展望，以期能为今后重大岩体工程建设提供参考.

表1 中国近十年地质灾害数据统计

图2 由多孔介质和宏观裂隙构成的岩体[9]

1 水力耦合裂隙岩体力学特性研究

1.1 水力耦合岩体变形和强度特性研究

目前对于岩体力学特性的研究已取得丰富的成果[13-14]，许多学者在此基础之上进行了水力耦合作用下岩体力学特性的研究.Otto等[15]通过水力耦合试验获得了岩石变形的一些基本特性，如图3(a)所示，利用应力-应变曲线上的阈值特征点把岩石变形过程分为3个阶段，且从体积变化曲线中可知岩石发生扩容现象.Souley等[16]把岩石变形过程划分为5个阶段，如图3(b)所示，这一划分方法与无水压作用下岩石变形规律基本一致[17].张蕊等[18]把岩石应力-应变-渗透系数曲线划分为7个阶段，如图3(c)所示.文献[16,18]中也都存在明显的扩容现象.朱珍德等[19]针对花岗岩和灰岩试件选取3种不同水压进行了水力耦合试验，从变形曲线可知水压力对岩石峰值强度是有一定影响且作用明显.邢福东等[20]对比分析了大理岩和中细砂岩在高围压和孔隙水压下的力学行为，如图4所示，砂岩在有无水压时应力-应变曲线变化趋势基本一致，而大理岩无水压时峰后延性较好.两种岩石试样的弹性模量都比无水压时大.试验还表明水压力会加速岩石变形破裂速度、增加脆性、降低岩石强度，围压的增大会抑制水压对强度降低的影响程度.Otto等[15]为了很好地研究岩盐在水力耦合下的变形特性，采用超声波(UT)和渗透率测量相结合的方法，对损伤过程进行连续监测.研究发现，随着应力增大进而引起微破裂、孔隙裂缝变宽、渗透率增大并导致岩盐膨胀.仵彦卿等[21]从细观角度出发，利用CT扫描机对水力耦合试验过程进行实时观测，如图5所示，图中白色代表高密度物质，黑色代表低密度物质.通过试验发现岩石渗透特性与变形破裂过程息息相关，水压的存在导致试样强度损失10%.

综上可知，目前关于水力耦合岩石力学特性的研究尚处在发展阶段，大多研究是从力学试验获得的应力-应变曲线展开的[22]，试验研究和分析方面尚不全面，而随着声发射、CT扫描等新的辅助设备的运用可以从细观上深入细致的研究岩石裂纹变形破坏的特征[23-25]，运用新的力学理论和试验技术，在更深的层次上探究水力耦合下岩石变形的细观物理机制，并从细观角度上反映岩石宏观力学性能，构建宏细观之间的关系，这为不断发展和完善水力耦合机制奠定了基础.

图3 水力耦合作用下岩石压缩变形特性[15-18]

图4 60 MPa围压下岩石三轴压缩全应力-应变曲线[20]

Fig.4 Complete stress-strain curves of rock specimens under triaxial compression with 60 MPa confining pressure[20]

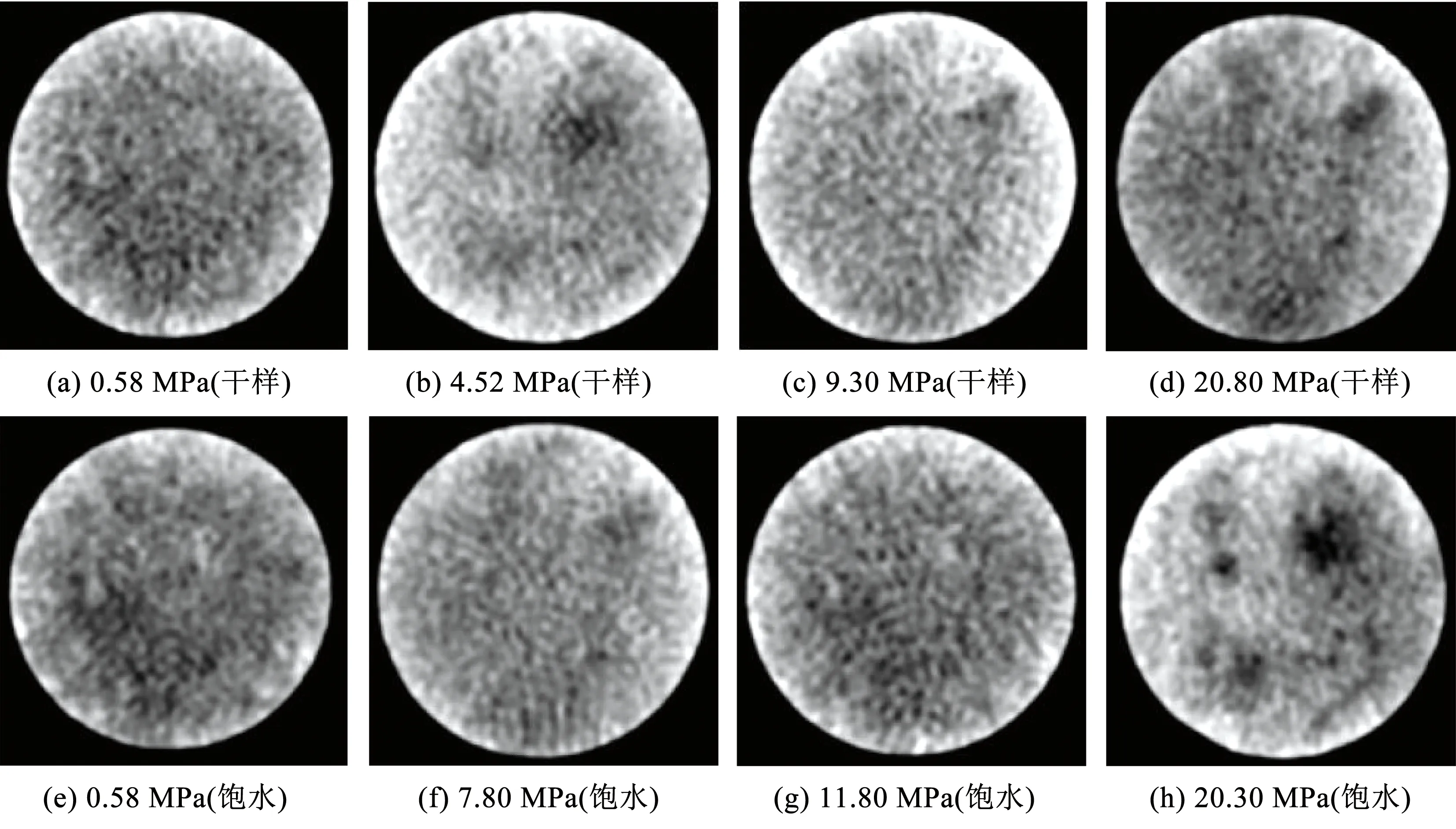
图5 砂岩试样不同应力状态下CT影像[21]

1.2 水力耦合裂隙岩体变形和强度特性研究

通过文献查询发现水力耦合裂隙岩体变形和强度特性的研究相对较少，但近年来仍有一些学者开展了相关研究.陈红江[26]通过对预制不同倾角单裂隙类岩石(圆柱标准件)在不同围压和不同水压下进行水力耦合试验，结果表明在裂隙倾角和围压一定时，裂隙起裂强度和弹性模量都随着水压力的增加逐渐减小；在裂隙倾角和水压力一定时，裂隙起裂强度和弹性模量随着围压的增加逐渐增大；在水压力和围压一定时，裂隙起裂强度在倾角为30°时最大，60°时次之，45°时最小，弹性模量随着倾角的增加变化不明显.周志华[27]通过对预制单裂隙长方体试件(200 mm×160 mm×100 mm)进行水力耦合试验，在单轴压缩水力耦合加载下随着裂隙倾角的增加峰值强度先减小后增加，倾角为45°时对应的峰值强度最小.在循环荷载下，有水压作用下的试件变形大于无水压时，在渗透水压作用下试样的抗压强度都降低.Kou等[28]通对预制45°单裂隙类岩石进行水力耦合试验，从图6(a)可知，随着水压力的增加，试样峰值强度不断降低，峰后变形中偏应力下降程度随水压的增加而增加.从图6(b)可知，峰值强度随着围压的增加而增加，并且随着围压的增加，峰后变形中的应变软化程度也逐渐增加.文献[26-28]表明水压对岩石力学性能的降低具有显著影响，并且导致峰后变形中的应变软化程度逐渐降低.Lee等[29]建立了测量岩石裂隙流速、法向位移以及剪切位移的液压力学测试系统，如图7所示，研究了人工预制粗糙裂隙花岗岩和大理岩试样在直剪过程中的水力性质，结果发生了明显的膨胀变形，极大地影响了粗糙拉伸裂缝的水力行为.上述试验与研究工作都充分反映出水压的存在对岩石力学特性有重要影响.但上述研究忽略了水力耦合下预制裂隙岩石的裂缝开度、裂缝长度、裂缝表面积等因素对裂隙岩石变形和强度的影响，此外，可利用损伤力学和断裂力学的理论，引入损伤变量分析裂隙岩石变形特性，结合声发射设备建立应力-应变曲线与声发射活动模式之间的对应关系，还可以借助于其他先进的观测仪器进行新的探索，不断丰富水力耦合裂隙岩体变形和强度特性的研究.

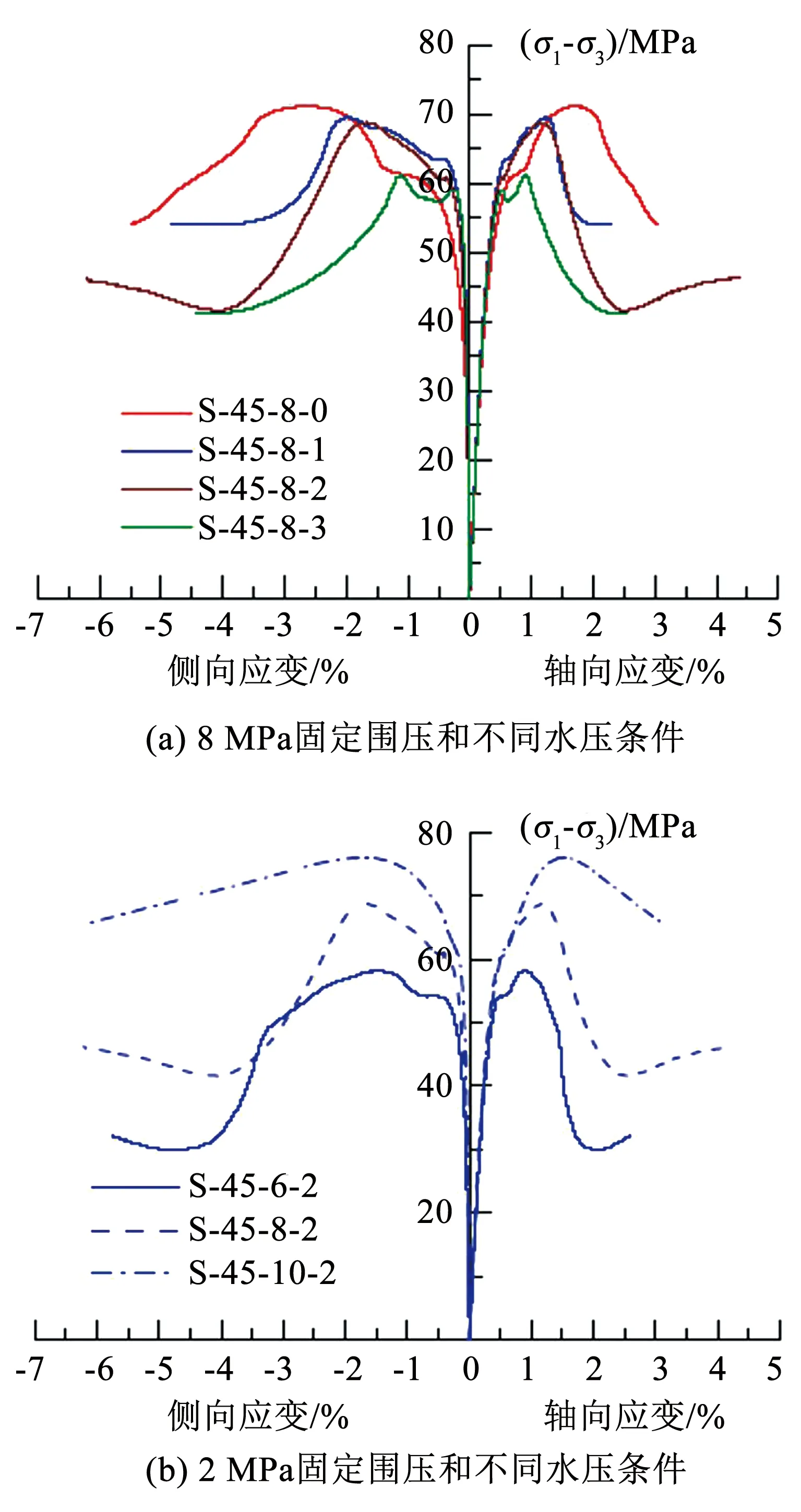
图6 预制α=45°倾角类岩石试样的轴向偏应力-应变曲线[28]

Fig.6 Axial deviatoric stress-strain curves of pre-fissured rock-like specimens withα=45°[28]

图7 直剪试验系统及实验结构图[29]

2 水力耦合裂隙岩体渗流特性研究

2.1 水力耦合岩体渗流特性研究

基于达西定律渗流力学，为使以岩(土)体为代表的多孔介质渗流研究得以不断地发展，许多学者对水力耦合岩(土)体渗流特性进行了深入研究，发现不同岩性岩石的渗透系数均与孔隙率大小成正比，指出岩石的细观结构变化以及非均质性对渗透性产生较大影响.从图3的渗透系数(渗透率)曲线可知，大多岩石在压缩变形过程中渗透系数(渗透率)随着应力的增加先出现下降趋势，到达最小值后开始不断增加，达到峰值后渗透系数(渗透率)下降并趋于稳定，文献[30-32]中也得出类似的规律.Mordecai等[33]在三轴应力条件下对砂岩破裂时渗透率的变化进行了研究，结果表明砂岩破坏后渗透率可增加20%.文献[34-35]研究了岩石有效压力与渗透系数的关系，如图8(a)所示，水力耦合作用下渗透系数与有效压力的关系经历了3个阶段.文献[36-37]研究了岩石有效围压与渗透系数的关系，如图8(b)所示，水力耦合作用下的页岩、花岗岩和致密砂岩渗透系数随着有效围压增大而减小.峰后岩石渗流研究是长期以来学者们面临的难点，由于岩石峰后产生大量裂隙且裂隙分布错综复杂，研究起来较为困难.如图9所示[38]，岩体压缩经历了从完整岩体-块体岩体-较破碎岩体-极破碎岩体的变化过程，其中涉及了尺寸效应、各向异性与各向同性的相互转化，将表现出不同的渗流特性，在今后的研究中要引起高度重视.因此，要加强对不同尺寸、不同粒径岩石渗流特性的室内试验研究，准确评价岩石的渗流规律对于岩体工程的安全实施具有重要的指导意义，此外，可以采用核磁共振技术测定岩石的孔隙率、渗透率等基本物理属性，在岩石渗流试验中核磁共振技术的应用能快速、准确、直观地观测到岩石内部流体的渗流过程及变化规律，为岩石微细观孔隙结构的深入研究提供了新思路.

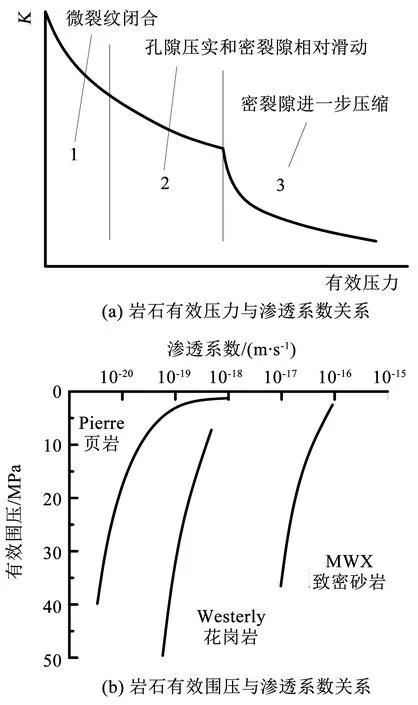
图8 岩石有效压力与渗透系数关系[34-37]

Fig.8 Relation between rock effective pressure and permeability coefficient[34-37]

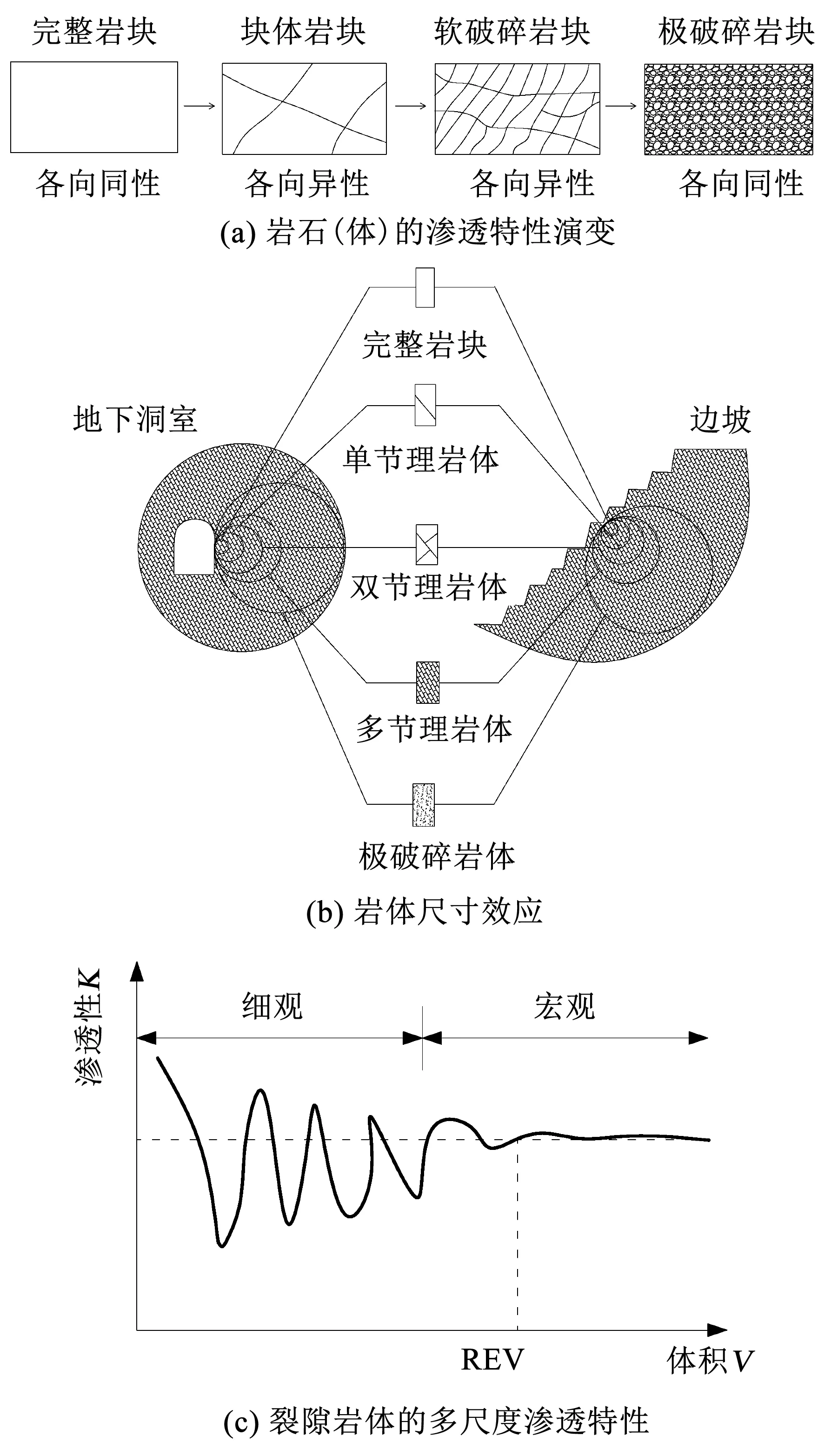
图9 岩石(体)渗流特征的尺寸效应[38]

2.2 水力耦合裂隙岩体渗流特性研究

2.2.1 单一裂隙岩体渗流特性

裂隙岩体由孔隙-裂隙构成，具有各向异性与非均质性，比孔隙岩(土)体更加复杂，因此，对裂隙岩体渗流特性的研究要比孔隙岩(土)体晚.裂隙岩体系统中复杂的岩体裂隙网络对流体的流动行为起着重要影响，研究单一裂隙渗流规律对确定复杂裂隙网络流体流动行为有十分重要的意义.许多学者从三方面对此进行了大量研究.

表2 单一裂隙立方定律修正公式汇总

第二方面从单一裂隙渗透(导水)系数与正应力之间的关系进行研究.Snow[46]通过试验获得水平裂隙渗透系数与裂隙的法向刚度之间的关系.Louis[47]根据试验结果指出裂隙渗透系数与法向应力呈负指数关系.Jones[48]、Nelson[49]和Kranz等[50]对不同岩性岩石的渗透系数进行了试验研究并建立了经验公式.Gale[51]和仵彦卿[52]通过室内试验结果指出裂隙导水系数、渗透系数与法向应力呈幂函数关系.具体经验公式汇总见表3，其中kn为水平裂隙渗透系数，k0为初始渗透系数，p0为初始压力，b为裂隙张开度，KN为裂隙方向刚度，s为裂隙间距，kf为岩石裂隙渗透系数，σ为法向应力，p为有效压力，ph为kf=0时的愈合有效压力，K为渗透率，a、k、A、B、n均为常数，S为过水面积，Pc为总压力，Pf为内部孔隙水压力，Q为渗流量，Tf为导水系数，D反映了裂隙分布的分维数，J为裂隙内水力梯度.此外还有大量关于裂隙渗透(导水)系数与正应力的试验研究，不再赘述.

表3 单一裂隙经验公式汇总

第三方面从单一裂隙渗透特性与剪应力(剪切位移)之间的关系进行研究.刘才华等[53]利用砂粒模拟粗糙裂隙，并研究在剪应力作用下剪动前粗糙裂隙的渗流特性，给出了渗透性随剪应力的增加而减小的规律.熊祥斌等[54]通过设计多组剪切试验研究了单裂隙在不同接触面积以及不同接触分布状态下的渗流规律.蒋宇静、夏才初、许江等[55-57]通过各自研发的试验机进行了类岩石、大理岩以及煤的剪切-渗流耦合试验.王刚等[58]指出类岩石在剪切试验过程中较小的剪切位移将导致裂隙渗透性的快速增大.

综上可知，学者们综合考虑了裂隙开度、裂隙粗糙度、裂隙渗透水压、裂隙面受力(正应力和剪切应力)等因素进行了单一裂隙渗流试验研究，这些因素导致单一裂隙渗流试验中岩体的渗流特性发生改变，呈现出不同的规律.目前室内试验研究主要集中在人为预制裂隙上，而尺寸效应、裂隙真实分布状态未充分考虑.从微细观到宏观研究单一裂隙渗流特性相对较少.今后仍需综合考虑各类复杂因素对立方定律进行修正，并且应朝着普遍适用性的方向发展，以便更好地描述单一裂隙岩体渗流特性.此外，从应力-应变曲线方面分析裂隙岩石变形破坏过程中的渗透特性，获得了与完整岩石渗透特性类似的规律，在此不再赘述.

2.2.2 裂隙网络渗流特性

单一裂隙岩体渗流特性尚未形成统一认识.天然岩体裂隙网络纵横交错十分复杂，研究难度更加艰巨.目前，裂隙网络渗流试验方面研究较少.张玉卓等[59]对含有4条不同裂隙宽度的大尺度岩体进行渗流试验，在不同加载方式以及侧压下获得渗流量与应力之间的关系为

Qz=a(1-bσx)4.

(1)

式中:Qz为z方向的渗流量，a、b为正常数,σx为x方向施加的边界应力.

田开铭[60]认为水流在隙宽不等裂隙中具有偏流效应，经过进一步的水力学试验研究，得出裂隙水流动的3个特征：偏向、偏流和阻力不等.速宝玉等[61]通过交叉裂隙水流试验，发现宽裂隙水头损失极小，窄裂隙反之.基于偏流效应使得优势流和交叉裂隙溶质运移等方面的研究逐渐成为热点.此外，三维裂隙交叉水流特性的机制及试验研究成果较少于二维裂隙情况且处于起步阶段.文献[62-63]研究表明三维裂隙网络渗流的主要特征，即存在局部水流环流现象.

综上，裂隙网络渗流试验的研究还不成熟，渗流试验规律尚无完全被揭露，复杂渗流现象仍需探究，目前缺乏对大尺度裂隙网络渗流特性的研究.由于裂隙网络自身的复杂性和不确定性，给试验设计及试验设备选取带来较大困难，因此对裂隙网络渗流试验的研究有待进一步加强.

2.2.3 充填裂隙岩体渗流特性

天然岩体裂隙中一般都含有破碎状岩土充填介质，在有无填充物情况下岩体裂隙的渗流特性存在显著的差异性，充填裂隙渗流特性的研究具有重要的工程价值与现实意义.文献[7,64-67]通过对充填裂隙进行渗流试验，获得一系列渗流公式(见表4).Carman在Kozeny的研究基础上推导出了充填砂中低速流体的运动公式[64].文献[65]根据Carman-Kozeny模型推导出了孔隙介质渗透系数公式.田开铭等[66]利用文献[64]中的公式提出充填裂隙渗流公式.速宝玉等[67]进行了预制充填裂隙渗流试验，利用文献[64-65]的公式提出了充填裂隙的渗透系数公式，但在该公式中未考虑裂隙面粗糙度的影响.张有天等[7]通过对充填裂隙岩样进行渗流试验建立了流量公式.表4中，c1为常数，u为流速，b为充填物裂隙宽度，α为颗粒形状系数，d为颗粒直径，n为充填颗粒的孔隙率，ν为水的运动粘滞系数，c2为常数，K为充填裂隙的渗透系数，Kp代表充填介质的渗透系数，Kf为未充填裂隙的渗透系数，bh为靠近裂隙壁面处的等效水力隙宽.另外，刘才华、陈金刚、于冰等[68-70]也对充填裂隙水渗流特性进行了深入研究，取得了丰富的成果.

表4 充填裂隙渗流数学公式汇总

Tab.4 Summary of mathematical formulas for filling fracture seepage

来源公式形式备注Carman(1927年)[64]u=n3c1(1-n)2d2gνJ经验公式明兹(1957年)[65]Kf=gn3d2184να2(1-n)2经验公式田开铭(1989年)[66]u=c2n3c1(1-n)2b2g12νJ=KJ,Kp=c2n3c1(1-n)2,K=KfKp经验公式速宝玉等(1994年)[67]K=gn3d220.4να2[1+3(1-n)db]2经验公式张有天等(2005年)[7]q=g(bh)36νJ立方定律修正

天然岩体裂隙中充填物质多种多样，不同性质的填充物对充填裂隙岩体的渗流特性产生不同的影响.岩体裂隙中的充填物质会对岩体结构变形和岩体结构强度产生重大影响，在渗透水压和应力作用下裂隙充填物质会发生滑动和流失，进而引起裂隙面变形，改变隙宽、粗糙度等几何结构，最终改变渗流路径.现在针对裂隙充填介质性质的研究成果较少.充填裂隙渗流特性不仅与裂隙隙宽、粗糙度等几何结构有关，而且与充填介质颗粒粒径尺寸和孔隙率等因素密切相关.在充填裂隙研究中应尽量选用天然岩体充填介质,同时要加强充填裂隙岩体剪切应力与渗流特性关系的研究.

3 水力耦合裂隙岩体变形破坏全过程研究

3.1 水力耦合岩体变形破坏全过程研究

水力耦合岩体变形破坏问题主要研究裂隙萌生、起裂、扩展及贯通破坏过程中的渗流与力学规律.目前，大多数的研究是通过把天然岩体加工成岩石试样并利用三轴压缩和剪切试验探究岩石损伤变形破坏前后的渗透率变化规律.李世平等[71-72]在国内最早开展岩石应力-应变-渗透率全过程试验研究，获得砂岩试样的应力-应变(σ-ε)和渗透率-应变(k-ε)曲线并归为3种类型，如图10所示，Ⅰ型渗透率极值kmax出现在应力峰值之前；Ⅱ型渗透率极值kmax出现在应力峰值之后；Ⅲ型渗透率极值kmax与应力峰值重合，出现3种类型的概率由大到小依次为

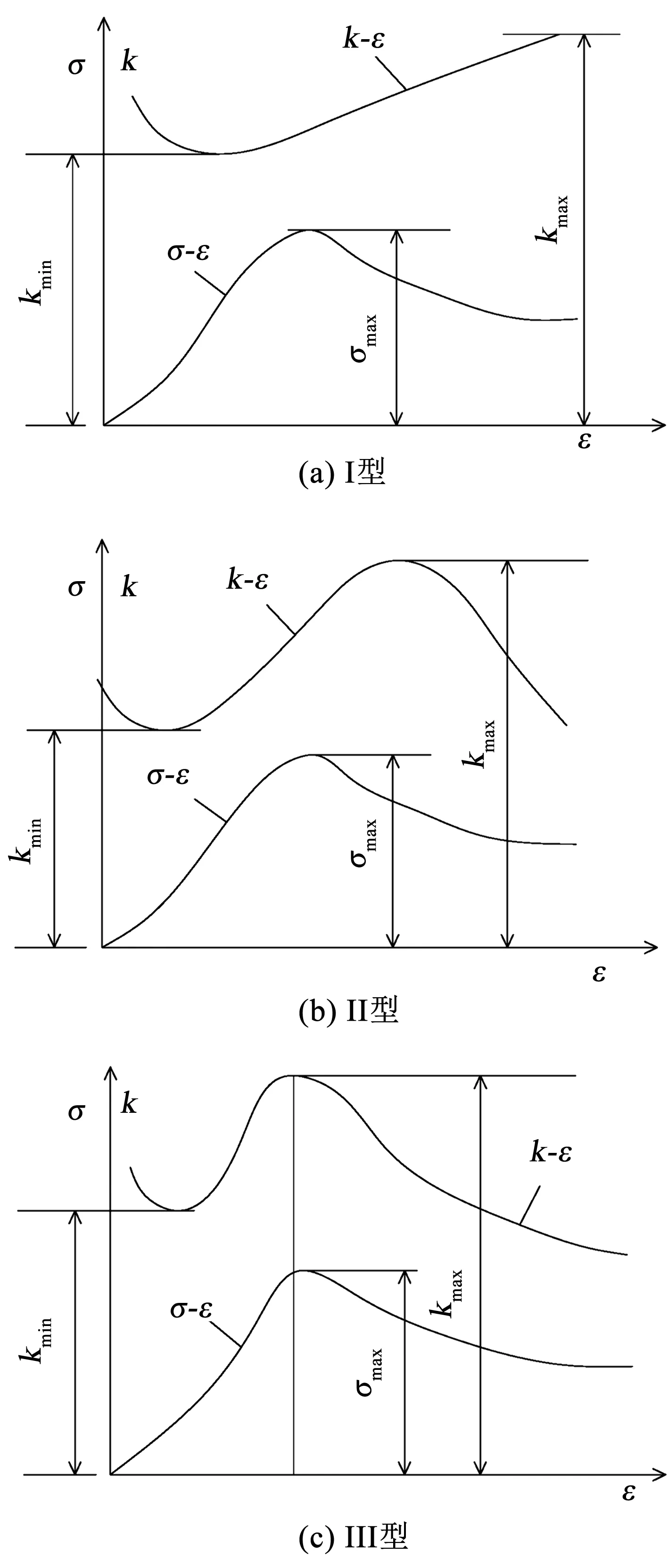
图10 不同类型的全应力-应变-渗透关系曲线[71-72]

Fig.10 Different types of complete stress-strain-permeability curves[71-72]

Ⅱ型、Ⅰ型、Ⅲ型.通过均差法拟合可知渗透率与轴向应力或应变之间符合多项函数关系.姜振泉等[73]对灰岩(硬岩)、中砂岩(硬岩)、细砂岩(硬岩)、砂质泥岩(软岩)、铝土岩(软岩)、粘土岩(软岩)进行了全应力-应变过程渗透性试验研究，认为软岩的渗透率在峰值前达到，破坏后渗透性随变形扩展而降低，硬岩的渗透率在峰值后达到，峰后压密阶段渗透性仍较大.彭苏萍等[74-75]通过对细砂岩、中砂岩的渗流-应力耦合试验研究也得到了与文献[73]关于硬岩研究相同的结论，即硬岩渗透率出现在峰值后.

王环玲等[76]通过试验观察到渗透率会出现突跳现象，并指出变形破坏峰值前后渗透压差与时间之间符合负指数函数关系.韩宝平等[77]通过对灰岩和白云岩的试验表明渗透率都会表现出突跳增大.Zhang等[78]的试验结果表明，渗透率不是恒定的而是应力的函数且符合指数形式，但变形处于非弹性阶段时，渗透率变化似乎是最不可预测的，峰值后渗透率产生明显突跳现象，与体积应变的变化具有关联性.陈振振等[79]通过选取锦屏二级水电站大理岩试样进行全应力-应变过程渗流试验，总结了渗透系数与体积应变之间的变化规律.李树刚等[80]通过对煤样全应力-应变试验过程中的渗透率与体积应变之间的关系进行了拟合，拟合结果符合多项式关系.朱珍德、邢福东等[19-20]在高围压高水压下对大理岩进行了全应力-应变三轴压缩试验，得出水压力会加速岩石破裂速度、降低岩石强度，围压的增大会抑制水压对强度降低的影响程度.王金安、王连国、卢平等[30-32]都采用MTS815.02电液伺服岩石力学试验机对渗透率演化规律进行了研究.近几十年，随着先进的试验设备不断被研发，声发射(AE)、偏光显微镜(PM)、扫描电子显微镜(SEM)以及CT扫描等先进的辅助试验技术被应用.许多学者利用先进的试验设备与技术对岩体渐进破坏过程中的水力耦合机制进行了研究.朱珍德等[19]研究了渗透水压力对脆性岩石损伤劣化的影响及脆性岩石渐进过程中渗透特性的变化规律，对比分析了岩石破坏断裂断口微观扫描电镜结果.Xiao等[81]采用高压三轴岩石自动控制系统(HPTAS)对红砂岩在不同渗透压力(pw)下进行了三轴压缩试验，分析了岩石破坏过程中强度、变形、轴向应变刚度(ξε1max)和渗透率的变化规律.试验表明，应力阈值随渗流压力的增加而降低，渗流压力不会影响应变刚度趋势，但会影响值的大小，如图11所示.在应力和应变变化的整个过程中，渗透率曲线先减小然后迅速增加，最终趋于稳定，并且渗透率曲线的峰值滞后于应力应变曲线的峰值.Zhou等[82]对北山花岗岩进行了常规的三轴压缩(CTC)和渗流-应力耦合(HM)试验，并采用声发射(AE)空间定位系统监测岩石渐进破坏全过程，结果表明，在HM耦合下，裂纹闭合应力消失，裂纹起裂应力高于CTC试验.当达到损伤应力时，孔压可以促进裂纹发展.丁长栋等[83]基于偏光显微镜图像从微观角度对比分析了不同围加卸载条件下致密红砂岩在渐进破坏前后不可逆的变形破坏机制，如图12所示，进而研究了渗透率的演化规律.由上面综述可见，对水力耦合岩体变形破坏全过程的研究已取得大量成果，先进试验设备的使用也成为了趋势，从细观角度出发发现了许多常规试验研究中未能解释的裂纹萌生与扩展的细节变化，很好地反映了宏观破坏的本质特征，有助于阐明水力耦合岩石破坏过程的机理.

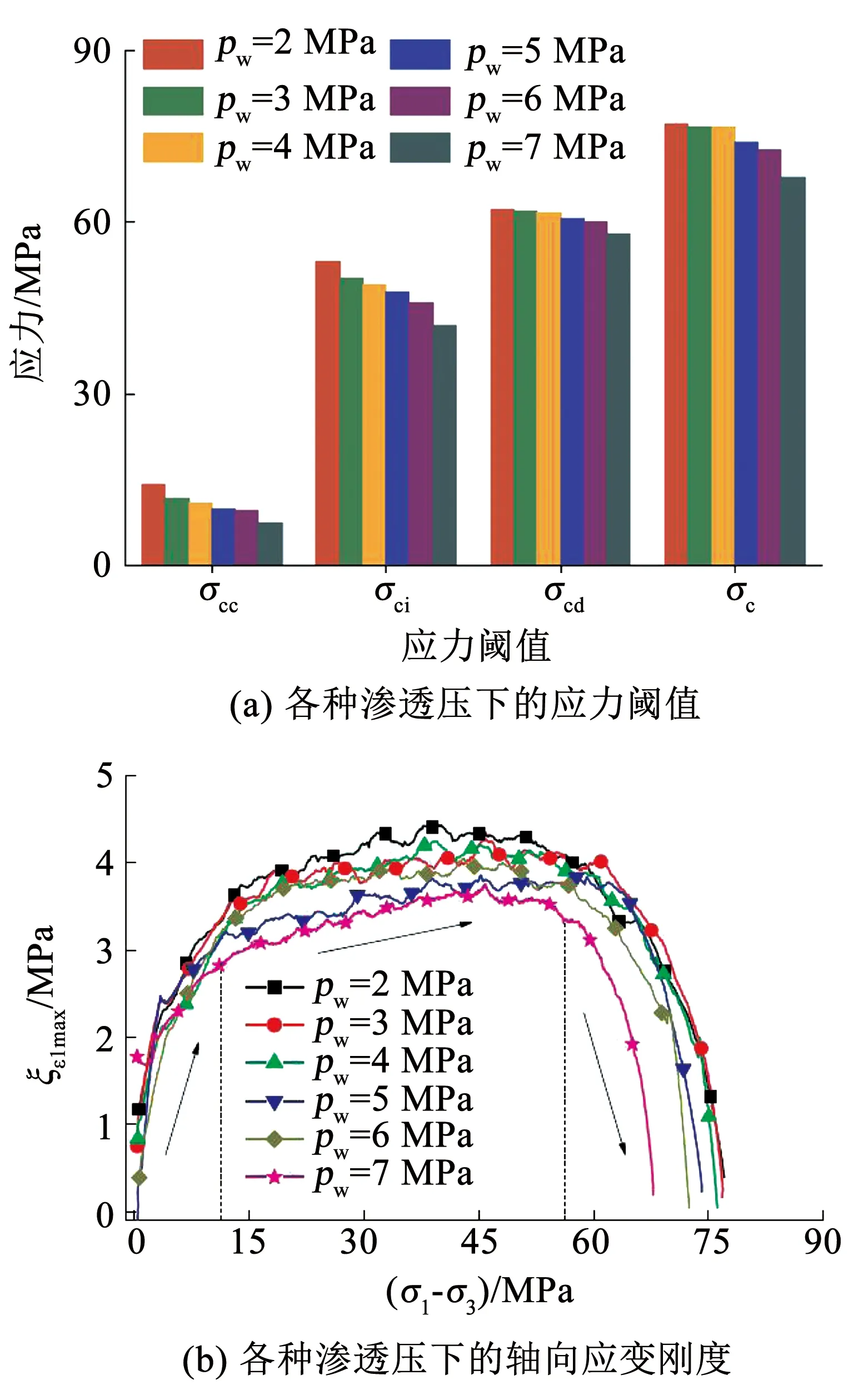
图11 渐进破坏过程中各种渗透压下的应力阈值和轴向应变刚度[81]

Fig.11 Stress thresholds and axial strain stiffness under various seepage pressures during progressive failure process[81]

3.2 水力耦合裂隙岩体变形破坏全过程研究

陈红江[26]分析了预制单裂隙类岩石的应力-应变-渗透系数曲线，从曲线中可知渗透系数在压密阶段有减小趋势，在弹性阶段渗透系数出现最低点，在裂纹扩展阶段渗透系数急剧增加，渗透系数峰值出现在峰后应变软化阶段，同时峰后的渗透系数值大于峰前，岩石渗透系数同样出现突跳现象.周志华[27]通过分析预制单裂隙长方体类岩石试件获得与陈红江[26]同样的结论.Lin等[84]为研究裂隙岩石在渗透压下的强度和破坏机制，人工预制了不同裂隙倾角的砂岩试样，并建立了单轴渗流-应力加载装置，并与声发射(AE)系统结合使用，在有(无)渗透压的情况下进行单轴压缩试验.如图13所示，在渗透压下的样品峰值强度远低于无渗透压的样品，但在峰值应变下保持领先.如图14所示，Zhao等[85]对带有锯齿形凹凸的人工节理进行了一系列常规的剪切试验和剪切流固耦合试验.对剪切全过程中的剪切变形、强度变化和渗流特性进行了综合分析，以揭示节理粗糙度、法向应力和渗流压力对剪切-渗流耦合行为的影响.对于水力耦合裂隙岩体变形破坏全过程的研究可充分参照完整岩体的研究思路与方法，但此研究的难点在于真实岩体人工裂隙在特定条件下的预制，且预制裂隙的精度往往难以达到试验设计的需求，所以多采用浇筑的类岩石试样进行试验，今后需加强真实岩石试样的研究.

3.3 水力耦合裂隙岩体变形破坏模式研究

周志华[27]分析了预制单裂隙长方体类岩石在无渗透水压和渗透水压参与下单轴压缩裂纹的破坏模式.从图15可知，无渗透水压作用下预制裂隙端部较破碎且有较多微小翼裂纹，渗透水压作用下预制裂隙端部破碎裂隙较少且产生明显翼裂纹.通过对比可知渗透水压可以减小裂纹面上的摩擦力，并促进裂纹起裂和扩展.Lin等[84]基于前人的研究把裂纹类型分为：张拉翼裂纹(Ⅰ)，张拉裂纹(Ⅱ)，反翼裂纹(Ⅲ)，混合裂纹(Ⅳ)，远场裂纹(Ⅴ)和表面剥落(Ⅵ).在有无渗透压作用下预制不同裂隙角度砂岩破裂方式如图16(a)、16(b)所示，此外，裂隙角度较小(0°～30°)的试样主要受拉伸破坏，中等裂隙角(30°～60°)的试样主要受剪切破坏，裂缝角度大(60°～75°)的试样容易发生拉伸-剪切破坏.Zhao等[85]通过水力耦合作用下的剪切试验很好地观察到了剪切破坏模式，如图17所示，当渗透压力为0.5 MPa时，剪切接处表面几乎完好无损，而在较大的渗透水压力下，产生明显的滑动剪切特征，在图17(c)中，可以在1.5 MPa的渗透压力下清楚地观察到一些污泥区域，这反映了软化作用的存在.由于样品的圆柱形状，随着剪切试验的进行，接触区域会变小，因此在每个表面的中心都会出现完整区域.Kou等[28]通过实验研究了预制单裂隙类岩石材料在水力耦合作用下的变形破坏行为.结合CT扫描和3D重建技术分析了破坏后预制裂隙类岩石试样的裂隙空间分布规律，如图18所示.从破碎的样品和表面破坏模式中观察到共面剪切裂纹和倾斜剪切裂纹是从预制裂隙尖端开始的，远场剪切裂纹与预制裂隙尖端产生的斜向剪切裂缝连接，从而导致类岩石试样最终发生纯剪切破坏，内部破坏模式受围压和内部流体压力的影响.此外，利用扫描电子显微镜(SEM)的观察发现，随着内部流体压力的增加，微观尺度上裂纹萌生区域的断裂表面粗糙度降低.付金伟[86]、曹加兴等[87]采用透明树脂材料研究了水力耦合的渐进破坏规律，对比分析了有无水压作用下试件的破裂模式.郭孔灵等[88]通过预制三维椭圆形裂隙试样进行水力耦合试验，详细分析了有无水压下长方体裂隙试样的破裂模式，结果可知，随裂隙倾角增加，破裂模式从张拉为主转变为拉剪复合再转变为剪切为主；随着水压的不断增大，逐渐增强了张拉破裂，减少了剪切破裂.此外，Liu等[89]在室内三轴渗流试验的基础上，分析了充填料裂隙砂岩的渗透特性，给出了其破坏模式.

图13 裂隙角度对含缺陷砂岩试样强度和变形参数的影响[84]

Fig.13 Effect of fissure angle on strength and deformation parameters of sandstone specimens containing flaws[84]

图14 人工节理试样图(mm)[85]

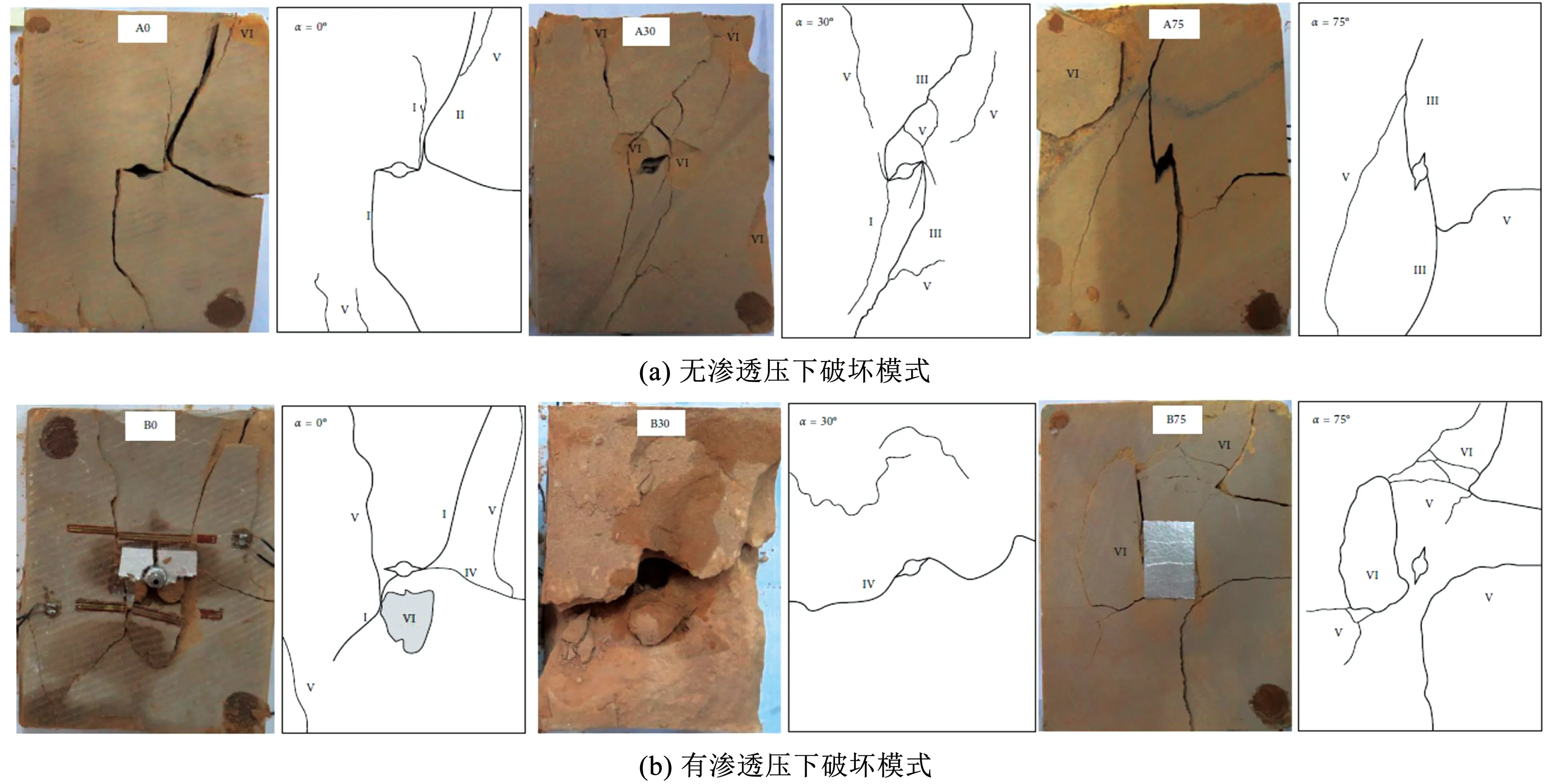
图16 含不同裂隙角度的砂岩试件最终破坏模式[84]

图17 法向应力为2.5 MPa、节理粗糙度为15°时进行剪切-渗流耦合试验后节理表面图[85]

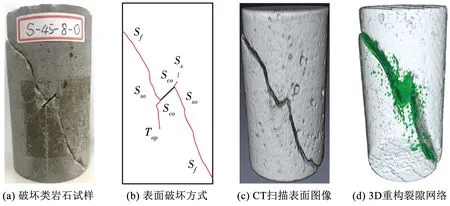
图18 破裂的预制裂隙类岩石试样的CT图像三维重构[28]

综上所述，完整岩石水力耦合试验研究已取得丰富的成果，采用先进的试验设备很好的了解到岩石渐进破坏与渗流特性演化过程的规律.但是，预制裂隙岩石的水力耦合试验研究还相对少见，岩石中预制裂隙的存在使得水力耦合问题更加复杂，为了弄清其机制，耦合试验研究仍应朝着微细观、可视化等方向发展.

4 水力耦合裂隙岩体变形破坏数值模拟研究

近些年，随着计算机的飞速发展，为水力耦合裂隙岩体问题的深入研究提供了新的方法.国内外许多学者在水力耦合数学模型理论和数值分析方法等方面进行了大量研究，取得了丰硕的成果.本节重点归纳总结国内外学者采用的耦合模型和数值分析方法.

4.1 理论模型

水力耦合是多场广义耦合的一部分，水力耦合主要研究固体介质和流体间相互作用的力学规律.关于水力耦合理论模型的基本假设、控制方程、边界和初始条件可参考文献[13].经典的水力耦合模型分别为：等效连续介质模型(ECM)、裂隙网络模型(FNM)、双重介质模型(DM).通过对文献[90-93]进行归纳，总结了各种模型的特点、数学方程表达式及优缺点.

4.1.1 等效连续介质模型(ECM)

ECM假设裂隙岩体空隙性差且相互连通，水流可分布整个岩体介质中且裂隙导水性较好.将裂隙中水流等效平均到岩体中，可以用连续介质理论表征裂隙介质及其水流的各向异性，以岩体渗透系数张量描述岩体的渗透特性.数学方程[90-93]为

(2)

(3)

式中：kf为渗透率张量，Kf为渗透系数张量，d为裂隙平均开度，λ为裂隙平均密度，a为裂隙面的法方向单位矢量.

ECM的优点：模型简单、使用方便、应用最为广泛，优先用于裂隙岩体表征体单元体积(REV)小于研究域的1/20～1/50的情况.ECM的缺点：该模型一般认为岩体中水流运动服从达西定律，并不适用于非线性渗流的分析.

4.1.2 裂隙网络模型(FNM)

FNM假设岩体裂隙介质分布具有单一性、呈几何形态、规律性等特点.充分考虑岩体结构中的裂隙产状、间距、隙宽、大小、形状、位置等几何参数，能很好的描述水流动特征.数学方程[90-93]为

(4)

式中：x、y均为局部坐标轴，Kx、Ky分别为沿x轴和y轴的主渗透系数，p为水压力，S为贮水系数，W为源汇项.

FNM表征小尺度且裂隙少的工程问题具有精度高、接近实际等优点.其缺点则不适用于大尺度裂隙多的模型，计算量庞大，难以或无法实现.

4.1.3 双重介质模型(DM)

DM的空隙结构由岩块裂隙和孔隙构成连续介质，孔隙、裂隙之间流量实时交换.裂隙岩体双介质中裂隙介质具有导水好、贮水弱的特点；孔隙介质具有贮水强、导水弱的特点.数学方程[90-93]为

(5)

(6)

式中：Kp、Kf分别为孔隙岩块和裂隙介质的渗透系数，Sp、Sf分别为孔隙岩块和裂隙介质的贮水率，α为孔隙岩块与裂隙介质之间的水量交换系数，Hp、Hf分别为孔隙岩块与裂隙介质中地下水水头.

DM综合考虑了等效连续介质和裂隙网络介质的优点，解决了耦合精度和可操作性之间的问题，符合实际裂隙岩体，适用大尺度裂隙介质渗流问题，有较好的发展前景；其缺点是计算量大，水量交换系数较难确定，裂隙介质非均匀性和各向异性不能很好体现.

目前经典的水力耦合模型用于真正解决实际工程问题还存在一定差距，水流在裂隙岩体中的流动行为是一个相当复杂的过程，因此必须不断完善和发展经典耦合模型或构建新的耦合模型来研究裂隙岩体中的渗流问题.经典方法显然不能全面模拟水力耦合下岩石变形破坏全过程，文献[13,94-95]总结的基于断裂力学的离散微力学模型(DMM)、连续损伤力学模型(CDM)、统计模型(SM)以及混合模型(DMM/SM、CDW/SM、DMM/CDW)都能很好地模拟岩石破裂问题.Vandamme等[96]基于DMM模型模拟了水力压裂变形破坏全过程，获得了渗透率变化规律.Valko等[97]和Souley等[16]使用CDM模型分别模拟了岩体水压致裂和水力作用下的洞室开挖.Shao等[98-99]通过DMM/CDM混合模型对脆性岩石裂纹渐进破坏规律及渗透特性进行了研究.Yuan等[100]利用CDM和SM模型清楚地说明了围压的增加使岩石变得更具延展性，整体渗透率降低了，可见流体流动方式与损伤变形之间的关系紧密相关.总之上述模型尚不成熟，亟待完善，其耦合模型本构、参数选取都应进一步深入研究.

4.2 数值方法

岩石力学中常用的数值方法分类汇总于表5，每种方法的具体原理可参考文献[13,101-102].近些年，许多学者应用离散元、颗粒流、非连续变形分析法等离散介质方法，扩展有限元法等连续介质方法，连续-非连续介质结合方法对裂隙岩体水力耦合问题进行数值分析，能够较好地表征水力耦合作用下裂隙岩体的损伤、破裂、贯通、块体滑动等过程.其中有限元法在分析工程问题中较为常用.赵延林[11]为在王庄煤矿工作面煤层进行高压注水致裂软化煤层的工业实验，采用有限元方法对注水过程中煤层的润湿损伤变形破坏进行了模拟研究.文献[103-106]采用二、三维有限元耦合程序分析了坝体、坝基、坝肩及库岸边坡的稳定性.师文豪等[107]通过COMSOL软件对层状边坡各向异性岩体水力耦合模型进行了数值模拟计算，模拟结果表明潜水面与实际情况基本一致.李廷春等[108]采用FLAC3D软件中的三维流固耦合模块对海底隧道开挖后的应力、位移、水压力分布进行了模拟分析，以期为隧道的稳定性提供有益参考.此外，应用较广的还有采用连续介质方法研究非连续介质问题的RFPA方法.李根等[13]基于RFPA方法模拟了三维圆柱标准件在水力耦合作用下的变形破坏全过程，很好地模拟出应力-渗透系数-应变的关系曲线如图19所示.上述方法在实际裂隙岩体工程分析中可以获得比较接近实际的结果，但这些方法仍然存在一定的局限.针对不同的工程领域，这些方法不具有普遍适用性.但通过综合每种方法的优点，可以达到分析不同的工程领域问题的目的.多种数值分析方法互补联合是今后发展的趋势.

表5 数值方法特点汇总[13,101-102]

图19 试样应力、渗透系数与应变的关系及其对应的试样破坏模式[13]

5 存在问题及解决方法

5.1 水力耦合研究存在的问题

国内外学者们围绕水力耦合裂隙岩体问题，在变形和强度特性、渗流特性、变形破坏机制及数值模拟等方面开展了诸多积极有效的工作，取得了一系列实质性成果.然而，由于岩体内部裂隙介质形成的随机性、几何形状的多样性以及力学特性的复杂性，至今仍未完全弄清水力耦合裂隙岩体理论机制，相比岩体孔隙介质渗流理论还不够成熟，不足以解决各种工程水力耦合问题，其中，水力耦合变形破坏机制是裂隙岩体工程领域研究的热点和难点，需要人们长期坚持不懈的探索.目前具体存在以下几方面问题：1)在水力耦合裂隙岩体力学特性研究方面，鲜有从微观-细观-宏观多尺度分析裂隙岩体力学性质.2)在水力耦合裂隙岩体渗流特性研究方面，单一裂隙渗流特性研究中所采用的预制裂隙深度与宽度差异较小，且高度相似，但天然岩体在构造运动、风化作用等影响下形成物理特性差异较大的裂隙，所以试验中用于切割岩石裂隙开度的技术存在局限性，获得的结论和经验公式与实际存在一定偏差，缺乏考虑多种物理因素共同作用下对立方定律公式进行修正；对裂隙网络的渗流特性认识尚浅，目前侧重于数值模拟研究，缺乏试验手段进行验证.3)在水力耦合裂隙岩体变形破坏机制研究方面，主要集中在宏细观角度上，缺乏从微观角度上研究宏观裂隙岩体在耦合作用下的破坏失稳行为；目前尚未完全弄清楚水力耦合裂隙岩体变形破坏机制，对于裂隙渐进破坏过程中线性或非线性渗流特征、力学行为等规律难以给出正确合理解释.4)在数值模拟方面，不能准确获取真实可靠的岩体工程地质资料及渗流参数，导致无法定量化描述裂隙岩体结构.由于裂隙岩体基本参数的不准确，求解水力耦合问题时对耦合模型的选取将失去意义；现有的耦合模型均无法完全解决工程实际问题，且对理论模型、本构关系及计算方法等的选取未达成统一共识；在数值分析方法方面未能统筹多种数值方法的优势和特点，建立一套功能完善、性能高效、结果可靠的分析方法；数值模型尺度较大时，计算速度较慢.5)此外，天然岩体裂隙中的充填物对力学和渗流特性有较大影响，但对充填水力耦合裂隙岩体试验与机制方面的研究成果却不常见.对于渗流-应力-温度-化学等多场耦合的研究成果还有待深入.

5.2 水力耦合研究的意见与方法

通过总结分析了国内外水力耦合裂隙岩体研究现状，并进一步分析了现有成果中存在的问题，从解决实际岩体工程领域问题的角度出发，对水力耦合裂隙岩体的研究给出五方面的意见：

1)深化水力耦合裂隙岩体渗流特性研究.单一裂隙渗流规律是裂隙网络渗流特性研究的基础，并已获得广泛应用，但还需深入研究.本文认为水力耦合渗流特性应从以下几个方面着手：a)对单一裂隙渗流规律的研究切勿盲目把主要焦点放在修正立方定律上，应充分利用先进的技术确定此定律中一些难测参数，以便更好的工程应用；单一裂隙渗流试验研究主要集中在裂隙流量与隙宽指数n之间关系、裂隙渗透(导水)系数与正应力之间关系上的数学描述，且多为特定条件下得出的经验公式，今后研究中需进行进一步验证其正确性与合理性.b)在裂隙渗透特性与剪应力之间关系、裂隙渗透特性与三维应力之间关系上的研究相对较少，需进一步加强.c)岩体裂隙网络纵横交错十分复杂，试验研究无法很好地揭示其渗流特征，存在一定局限性，今后研究应结合数值模拟，相互验证，共同发展.d)从微细观角度出发探讨粗糙度、隙宽等物理因素发生微小改变对渗流特性的影响.e)设计新的单一裂隙岩石物理试验模型，采用粒子追踪技术或可视化录像系统对裂隙岩体中的渗流行为(渗流流体可添加颜色)实现实时描述.f)在上述基础上可进一步研究充填裂隙的渗流特征，加强对充填介质性质的研究，丰富充填裂隙水力耦合研究成果.

2)重点加强水力耦合裂隙岩体变形破坏全过程研究.水力耦合裂隙岩体变形破坏过程十分复杂，在渗透压和应力的作用下岩石初始介质细观结构发生损伤变化，进而改变岩石宏观力学性质和渗透性质，耦合过程实现了从微细观到宏观的尺度跨越.近年来，考虑岩体损伤破坏对渗流的影响越来越引起学者们的重视.研究工作具体从以下几个方面进行发展：a)采用声发射、超声、CT扫描等多手段相结合的辅助试验技术分析岩石从细观到宏观渐进破坏的整个过程，弄清工程施工中裂隙面开裂、压缩及剪切膨胀变形与渗流场的内在关系，以便反映水力耦合的本质特征，并逐步从宏细观分析转向微观分析.b)应加强高水压条件下的水力耦合裂隙岩石变形破坏全过程试验研究.c)大力开展三维条件下水力耦合变形破坏方面的研究.

3)构建合理的水力耦合数学模型.应根据岩体工程实际情况选用合适的水力耦合模型，但理论模型的选取是长期以来的难点.主要原因为实际岩体裂隙难以真实表征，构建的数值模型无法匹配实际工程，现有的经典耦合模型自身又存在诸多缺陷.因此，应不断发展现场测量技术和新的理论模型，使现场工程问题的研究建立在更符合实际的耦合模型上.具体从以下方面着手：a)大力发展真三维岩体结构面测量方法.b)在耦合模型建立时需考虑复杂应力状态下裂隙的非线性变形与渗流特征.c)二维耦合模型的构建无法真实表征实际工程情况，往往描述的是平面问题，存在很大局限性.需大力发展三维水力耦合模型.d)为构建合理可靠的裂隙岩体渗流-应力-损伤耦合模型，需使细观损伤演化过程定量化，这对于确定损伤演化与岩石宏观力学和渗流行为之间的关系具有重要意义.

4)大力发展裂隙岩体水力耦合数值方法.随着计算机不断更新换代，模拟大尺度耦合问题得以实现.因此，亟需发展新的数值分析方法，开发普遍适用的裂隙岩体水力耦合软件.这些分析方法及软件应朝着以下几个方面发展：a)总体上数值软件应符合模拟尺寸大型化、应用简便化以及计算速度高效化.b)计算速度方面应加强并行算法研究，同时还要不断提高耦合模型计算精度与可操作性.c)需进一步加强室内试验研究和现场监测数据分析以验证模拟结果的真实性与可靠性.d)对于裂隙岩体工程而言，采用连续介质方法或离散介质方法进行考虑损伤的水力耦合模拟研究都存在一定的缺陷，一种有前途的方法是将连续介质方法和离散介质方法相结合，即有限元-离散元耦合法.与此同时，无网格法、数值流形元法因其在模拟裂隙扩展方面的优势而逐渐兴起，因此，在数值分析方法方面需结合多种数值方法的优点，以便达到快速解决实际问题的目的.

5)完善水力耦合理论体系.裂隙岩体是一个十分复杂的不确定天然地质体，当前人们对其认识仍存在一定局限性，尽管学者们对水力耦合裂隙岩体机制已进行多年研究，也取得一些阶段性成果，但还有许多问题亟待解决.随着自然科学、岩体力学、渗流力学以及岩体水力学的基础理论不断发展与完善，可以更加客观、全面、综合地揭露流体在裂隙岩体中的流动规律，形成一套完善的水力耦合裂隙岩体理论体系.因此，仍需从以下几个方面继续作一些研究工作：a)从总体趋势上来看，应由饱和渗流向非饱和渗流发展、由稳定流向非稳定流发展、由达西流向非达西流发展、由单相流向多相流发展、由两场分析向多场耦合分析发展.b)从细节方面来看，在裂隙岩体渗流研究中，往往忽略了基质的渗透性，缺乏合理区分裂隙与基质的方法，因此，在耦合理论体系构建过程中要充分考虑基质的作用.c)基于合理可靠的裂隙岩体耦合模型，并结合工程实践，从微观层次上研究岩石水力耦合机制.

6 结论与展望

1)从水力耦合力学特性、渗流特性、变形破坏机制及数值模拟等方面综述了水力耦合裂隙岩体研究的现状，系统总结了完整岩体和裂隙岩体变形、强度及渗流特性.重点分析了水力耦合变形破坏机制的最新研究进展，梳理了声发射(AE)、超声波(UT)、偏光显微镜(PM)、扫描电子显微镜(SEM)以及CT扫描等先进的辅助试验技术在变形破坏分析中的应用.归纳总结了国内外学者采用的耦合模型和数值分析方法，简略阐述了水力耦合裂隙岩体数值方法在采矿工程、水利水电工程、边坡工程及隧道工程中应用情况.

2)指出了当前水力耦合裂隙岩体研究存在的问题，包括缺乏从微观-细观-宏观多尺度分析裂隙岩体力学性质；单一裂隙渗流、裂隙网络渗流以及充填裂隙渗流试验方法有待深化；水力耦合裂隙岩体变形破坏机制尚未弄清、岩体工程地质资料及渗流参数有待准确获取；水力耦合理论还不成体系，在试验方法、机制分析、数值模拟等方面仍需开展深入研究.

3)对水力耦合裂隙岩体的研究给出了指导性意见，认为要继续深化水力耦合裂隙岩体渗流特性研究、重点加强水力耦合裂隙岩体变形破坏全过程研究、构建合理的水力耦合数学模型、大力发展水力耦合数值分析方法、逐步完善水力耦合理论体系.

4)深埋油气储库、地下核废料处置库、高温地热开发等新兴岩体工程领域的研究系统将更复杂.多场-多相耦合现象普遍发生，这将成为今后长期发展的方向.依据裂隙岩体所赋存的地质环境，开展裂隙岩体多场-多相耦合体系作用机制的研究，共同推动水力学、岩体(土)力学、工程地质科学及工程热力学等各学科之间相互交叉融合，将对理论体系构建具有十分重要的意义和对工程应用具有广阔的前景.

5)关于水力耦合裂隙岩体的研究获得了一定的成果，但也应认识到随着传统岩体工程难度的不断增大，新兴岩体工程的不断涌现，裂隙岩体水力耦合、多场-多相耦合机制及数值仿真等方面仍然面临着一系列关键科学技术难题，上述问题的研究成果将是地下能源(石油和天然气)、工程及地质灾害预防等的理论基础和关键技术.水力耦合裂隙岩体研究的不断发展必将为中国经济发展和社会进步作出巨大贡献.