多层径向床仿生反应器的设计及优化

2020-06-10刘未了成有为王丽军

高校化学工程学报 2020年2期

刘未了, 成有为,2, 王丽军,2, 李希

(1. 浙江大学化学工程与生物工程学院, 浙江杭州 310027; 2. 浙江大学衢州研究院, 浙江衢州 324000)

1 前言

仿生反应器是一种新概念的固定床反应器[1]，其结构模拟了血液循环系统 (如图1 (a)所示)。血液循环系统的多级分布式通道结构 (如图1 (b) 所示) 最大程度缩短了血液在毛细血管的流程并降低了流速，使整个体系的压降得以降低。仿生反应器正是采用了类似的结构，其核心设计思路是通过多级分布式的进出料通道和径向渗透流动的薄床层来降低固定床的压降，因此，对于快速气固催化反应，可以采用细颗粒的催化剂来消除颗粒内扩散对反应速率的限制而又不增加床层压降。

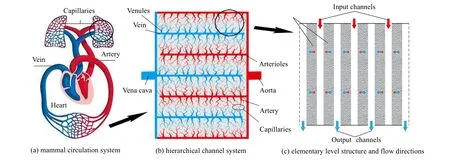
图1 仿生反应器概念示意图 Fig.1 Schematic diagram of the bionic reactor

图1 (c) 展示了仿生反应器的基础结构，流动方向如图中箭头所示。相比于传统固定床反应器，采用仿生反应器可以将压降减少一到两个数量级。根据应用的体系不同，仿生反应器有多种不同的实现形式，其中，多层径向床(multi-layer radial bed, MLRB)是一种典型的实现形式，它主要适用于大规模生产的快速催化反应，如甲醇制丙烯 (MTP)[2]、费托合成油裂解[3]、气相贝克曼重排[4]等。多层径向床由若干个薄层径向填充床组成，床层之间的缝隙为进出气通道，其结构剖面图如图2所示。多层径向床的床层及通道结构可由壁面可渗透的多孔堇青石蜂窝陶瓷构成[5]。通过解析分析和数值模拟来选择合适的床层厚度、通道高度与宽度，使得床层中流动和反应负荷分布均匀，并提高目标产物的选择性，是多层径向床仿生反应器设计及优化的核心内容。本文将通过对MTP这一应用案例的研究来展示多层径向床仿生反应器的设计及优化过程，并与现有的工业反应器进行性能对比，来体现仿生反应器在提高催化剂效率和目标产物选择性上的优势。

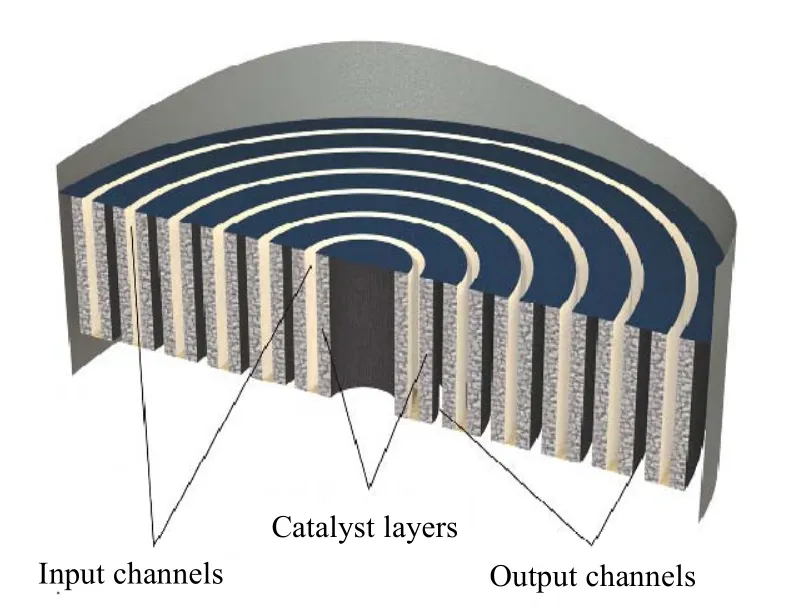
图2 多层径向床仿生反应器剖面图 Fig.2 Sectional view of the MLRB

2 数学模型和流动均布特性

2.1 多层径向床数学模型

径向床反应器是一种已被广泛应用的固定床反应器，其径向流速的轴向分布均匀性是影响反应器性能的重要指标，诸多研究也已阐明了其流动均布的特性。KAREERI等[6]研究了离心和向心，以及z型和π型这几种不同的流向下径向床流动均布的特性，BOLTION等[7]用电阻层析成像技术展示了径向床中流体的流动形态及速度分布，LI等[8]研究了两到三层不同的催化剂或吸附剂组成的径向床的流体力学特性，王恒[9]研究了高径比、内外流动截面积比等因素对z型和π型丁烯氧化脱氢径向床反应器流动均布的影响。上述的这些研究主要针对传统的大尺度单层径向床反应器的流动均布特性，并且结果主要由实验或模拟归纳而来。而仿生反应器是由若干个小尺度基础结构单元平行地组合而成，对于这种小尺度的基础结构单元，其通道尺寸对流动均布影响的灵敏度更高，因此，多层径向床仿生反应器的优化设计需要更加可靠的理论指导。

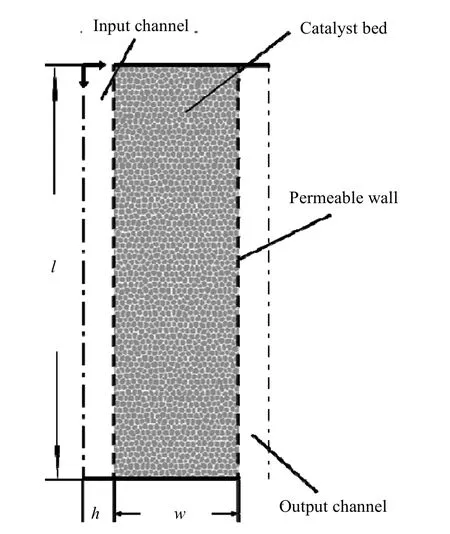
图3 基础结构单元几何模型 Fig. 3 Geometry of the MLRB elementary unit

多层径向床仿生反应器的基础结构单元可由一个简化的二维模型表示，如图3所示，其中包括进、出气通道和催化剂床层，流型为z型流动。由于仿生反应器采用小尺度的流体通道和薄床层，并且床层与中心对称轴之间留有一定距离，所以，环隙间的流动可近似视为平行板间的流动。基础结构单元的数学模型由表1给出，其中动量传递的耦合模型由进出气通道自由流动的Navier-Stokes方程组和床层渗透流动的Brinkman Forchheimer方程组成，质量和能量传递由对流扩散模型来表示。传热模型的进口条件为第三类边界条件。模型中用到的理想假设有：流体为不可压缩理想气体、催化剂填充床层采用拟均相模型且视为均匀的多孔介质、反应过程为绝热过程。模型方程中的渗透率B、扩散系数D、导热系数K及分散系数的估算式由表2给出。

表1 多层径向床仿生反应器基础结构单元数学模型 Table 1 Mathematical models for the MLRB elementary unit

表2 传递系数估算式 Table 2 Correlations for transport coefficients

2.2 模型验证

由于仿生反应器的研究尚在理论设计阶段，且课题未得到项目资助，当前阶段试验验证难以进行，将在一下阶段将其列为重点研究内容。因此，本研究通过具有类似数学模型的其他研究结果来间接验证。

本研究中的拟均相模型和均匀多孔介质的假设常用于气固催化反应的填充床研究中[16-17]，模型精度较为可靠。一般地，膜过程的流动模型常采用Stokes-Darcy-Brinkman耦合模型[18-19]。DAMAK等[20]的研究证实，对于通道雷诺数范围为300～1 000、渗透雷诺数范围为0.1～0.3的膜过程，Stokes-Darcy-Brinkman耦合模型具有足够精度。考虑到多层径向床仿生反应器中的流动可能会覆盖更大的雷诺数范围，所以在本研究模型中还加入了Forchheimer修正项以考虑惯性项对压降的影响。因此本模型在渗透流动偏离达西(Darcy)流动的情况下也依然具有足够的精度。在微通道反应器和膜反应器的传质和传热过程所用的对流扩散模型中，通道和床层区域通常具有不同的传递系数[21-23]，而多层径向床仿生反应器的传质、传热行为与微通道反应器和膜反应器类似。本模型中通道和床层的不同传递系数可由表2的关联式估算，并且还考虑了床层多孔介质的传质、传热分散，因此本模型具有足够高的可信度。

2.3 流动均布特性

本文作者在之前的研究[1]中，对式 (1) 进行了解耦、推导和求解，最终得到床层中渗流速度分布的解析表达式，并且验证了解析解与数值解的偏差在一定参数范围内可忽略不计。该研究提取了两个影响流动均布的关键参数Pr和Rew：

Rew是渗透雷诺数，而Pr的物理意义则是通道流动压降与床层渗流压降的比值。为了定量的表达床层渗流速度分布的不均匀性，引入径向渗流速度在轴向上的相对最大偏差σmax。对于z型流动的床层，σmax与Pr关系如表3所示，为分段函数关系式[1]。只要给出合理的床层渗流速度分布均匀性指标，就可以通过表3中的函数关系式得到准确的、优化后的尺寸参数。下面，以MTP反应为例来展示如何通过Pr指标对多层径向床仿生反应器的通道尺寸进行优化。

3 案例研究

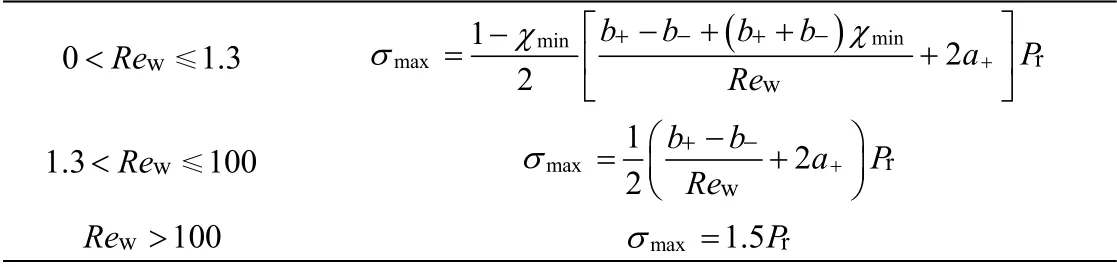
表3 不同Rew范围下σmax与Pr分段函数关系式 Table 3 Segmented function relations between σmax and Pr under different Rew ranges

3.1 案例背景

MTP反应是典型的大规模生产的快速反应。根据甲基化-裂化的反应机理[24]，C4～C6烯烃的甲基化反应是最快的，其次是C5～C7烯烃的裂化，C2和C3烯烃的甲基化反应是较慢的反应，而烷烃及芳烃的生成反应是最慢的副反应。因此，采用较薄的床层来控制停留时间以避免副反应的发生，是提高丙烯选择性的有效方法。目前工业上应用最广泛的多段Lurgi固定床反应器[25-26]，即采用六段饼状填充床层与中间冷激进料的方式。这六段床层最厚的不超过0.6 m，而直径则大于11 m，这样的尺寸设计正是为了在控制反应深度和床层压降的前提下保持足够的生产能力。而在如此大流动截面积的固定床中，难免存在径向上温度、反应负荷不均匀的问题；此外，为了降低压降，所填充的催化剂为φ2.8 mm×6 mm的大颗粒，对于最快速的主反应来说有极大的内扩散限制。WU等[24]、姜坤等[27]、朱嘉嘉等[28]分别研究了MTP的反应机理并得到了完整的HZSM-5催化剂上的本征动力学，在本文随后的研究中，均采用朱嘉嘉等的动力学数据进行模拟。通过催化剂颗粒模拟，得到φ2.8 mm×6 mm大颗粒催化剂对烯烃甲基化主反应的有效系数仅为46.6%[1]，因此大颗粒催化剂更有利于慢速的副反应的发生从而导致丙烯选择性的降低。综上所述，若在大处理量、高空速的条件下，采用小颗粒催化剂而保持低压降，并能够改善床层温度和负荷分布的均匀性，多层径向床仿生反应器是一个非常理想的选择。

3.2 参数确定

由于MTP反应需要中间冷激换热，多层径向床仿生反应器总体结构还是采用六段床层，而将原本饼状的固定床改为多层径向床 (见图4)。为了进一步减小床层阻力，多层径向床中装填中空圆柱型催化剂(见图5)。通过对催化剂颗粒的模拟，当颗粒尺寸为外径1.2 mm、内径0.4 mm、长度4.8 mm时，催化剂对主反应的有效系数可以达到90%以上。为了更有效地减少副反应的发生，前五段床层的停留时间限制在0.15s以内，仅保证最快速的甲基化反应转化完全即可。高碳烯烃裂化生产丙烯的反应将主要集中在第六段床层，因此，这一段床层停留时间控制在0.2 s以保证尽可能高的丙烯选择性。同时，经过初步估算，将每一个床层径向厚度w设为24 cm可以保证总压降不高于Lurgi固定床的总压降(0.03 MPa)。根据上述的床层停留时间可得床层渗流速度大于1.2m⋅s-1，远大于消除颗粒外扩散限制所需的最小气速0.19 m⋅s-1。

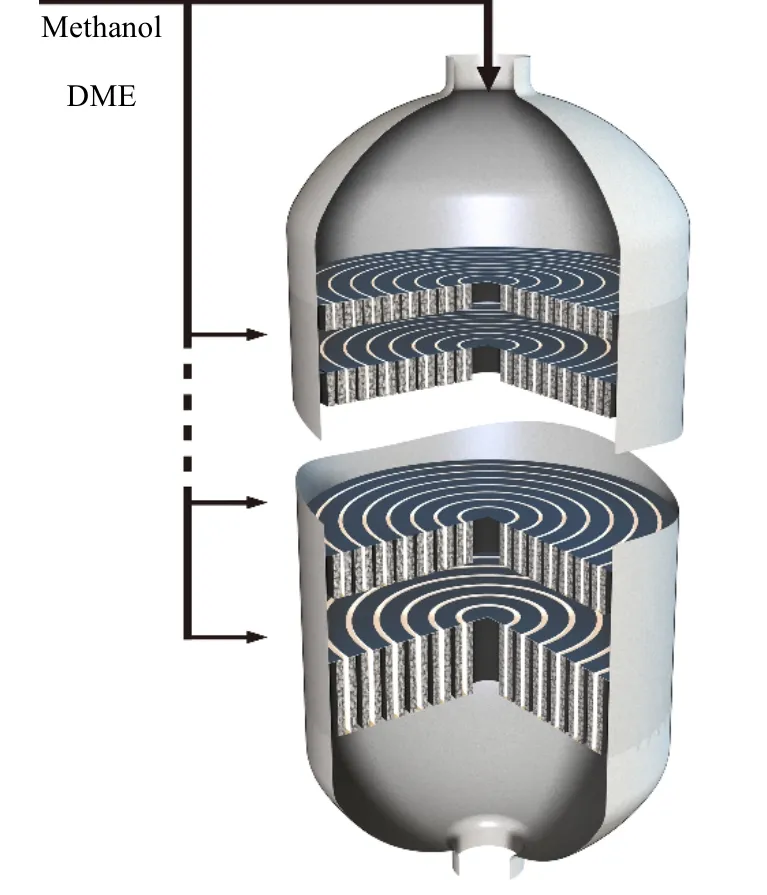
图4 多层径向床仿生反应器剖面图 Fig. 4 Sectional view of the MLRB

根据2.3节所述，通道尺寸(高度l和半宽h)由不同Rew范围下径向渗流速度在轴向上的相对最大偏差σmax与Pr关系式决定。显然，从反应处理量的角度来考虑，l/h越大，每一段床层的催化剂装填量越大，体积利用率越高；但是，根据其单调性可知，l/h越小，床层渗流速度的轴向分布越均匀。因此，在设计中应在满足均匀性指标σmax的前提下尽量提高l/h。

图5 中空圆柱型催化剂 Fig.5 Schematic diagram of a cylindrical hollow catalyst particle

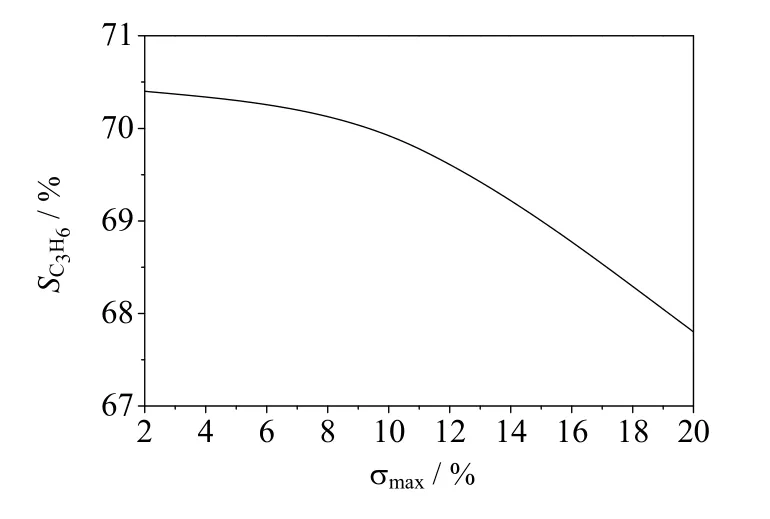
图6 丙烯选择性与相对最大偏差σmax关系曲线 Fig.6 Relationship between SC3H6 and σmax

由于床层渗流速度的轴向分布直接影响反应深度并最终影响丙烯的选择性，因此，通过对单段床层单程反应的模拟，得到σmax与丙烯选择性的关系曲线(图6)。由图可见，当σmax＞10%时，丙烯选择性将会低于70%并且迅速下降，所以将均匀性指标定为σmax≤ 10%。考虑到通道宽度为cm级、停留时间不大于0.2 s，虽然通道半宽h还未确定，渗透雷诺数Rew的值必远大于100，因此，根据表3，有σmax=1.5Pr，故Pr≤ 0.067。根据式 (14)可知，在停留时间tc一定、通过计算获得床层渗透率B、物性参数ρ和μ后，每一段床层的l/h最大值便可由Pr=0.067求得，于是σmax与Pr的函数关系即可转化为Pr与l/h的函数关系。进而，每一段通道的进口流速可根据u0= vwl/h得到。而确定l和h的绝对值，需要人为给定第一段床的初始的通道高度，之后下一段床的通道高度即可根据质量守衡和停留时间的限制条件求得。

多层径向床结构单元的局部放大图如图7所示，多孔堇青石骨架的结构为进、出气通道交替排布，催化剂装填在相邻的进出气通道之间。图中w、l和h分别为床层径向厚度、通道高度和通道半宽。

3.3 单程及循环模拟

由于每一层中间有冷激进料，所以每一段床层的通道高度和宽度都会有所增加，为了避免最后一段床层的通道高度过大，先初定第1段床层的通道高度l为50 cm。对多层径向床仿生反应器基础结构单元中的数学模型式 (1) ～ (3) 进行逐段计算来模拟单程反应，每一段床层的通道尺寸由上一段的出口及冷激混合物料的数据通过均匀性指标计算而得。最终六段床的操作条件及各段床层的通道尺寸计算结果列于表4。

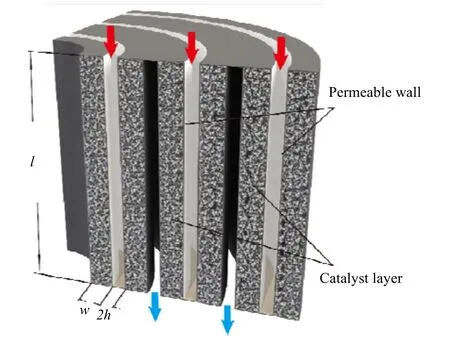
图7 多层径向床局部放大剖面图 Fig.7 Enlarged cross-section profile of the MLRB

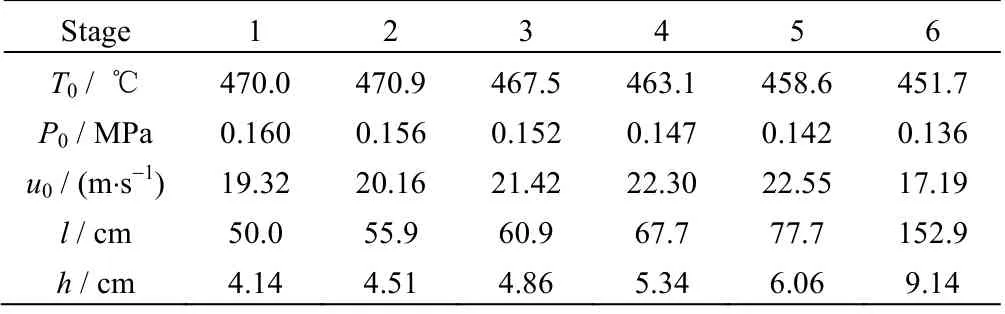
表4 单程反应操作条件及各段床层通道尺寸 Table 4 Single-pass operation conditions and geometric parameters for each stage

由表可见，通道高度和通道半宽逐段递增以满足停留时间及流动均布的要求。图8给出了各层渗流速度vw在轴向上的分布，其中，横坐标L为无量纲通道高度。由图可见，第1～第5层分布曲线相同，可以看出床层渗流速度在轴向的最大、最小值存在于顶端和底端，通过计算可得渗流速度在轴向上的相对最大偏差σmax小于10%，即满足了流动均布的要求。对于多层径向床仿生反应器单程反应，由于采用小颗粒催化剂显著提高了催化剂的有效系数，并且降低了前五段床层的停留时间，从而抑制了副反应的发生，丙烯的选择性达到70.9%，相比于Lurgi固定床反应器的单程丙烯选择性65.4%，提高了约6个百分点。

再按照工业生产中烷烃和烯烃的循环比进行循环模拟[29-30]。在循环模拟的过程中，每一段床层的通道尺寸计算方法同上，而第1段床层的通道尺寸则由分离之后的循环物料和新鲜进料的数据计算，并始终保证流动均布的要求。当循环组分及六段床层的所有尺寸都不再变化时，可认为循环模拟达到了稳态。最终循环模拟达到稳态时的操作条件和各段床层的通道尺寸如表5所示，第1段进口、第6段出口及中间冷激物料组成如表6所示。由表5可见，与单程反应相比，由于烷烃和烯烃的循环，床层内流量增加，导致通道高度与通道半宽也相应增加，最终六段床层总高度达到5.15 m。

循环模拟达到稳态时，第6段床层中C2～C6烯烃组分的摩尔产率PM(C2～C6烯烃组分的径向摩尔流量与总催化剂质量之比) 变化曲线如图9所示。由图可见，除丙烯外，其他烯烃的摩尔产率在各段床层中变化不大，这也说明循环模拟达到了稳定状态。从图9中丙烯曲线的斜率可以看出，丙烯生成速率最快的是第1和第6段床层，这是因为，第1段床层中由于分离循环后丙烯浓度较低，而甲醇、C4～C6烯烃浓度较高；第2～第5段床层中由于甲醇、C4～C6烯烃浓度降低且停留时间较短，以甲基化反应为主，故丙烯生成速率较低；第6段床层中由于C4～C6烯烃在前几段床的积累，再加上停留时间的延长，所以，以裂解反应为主，故生成大量丙烯并接近反应平衡。

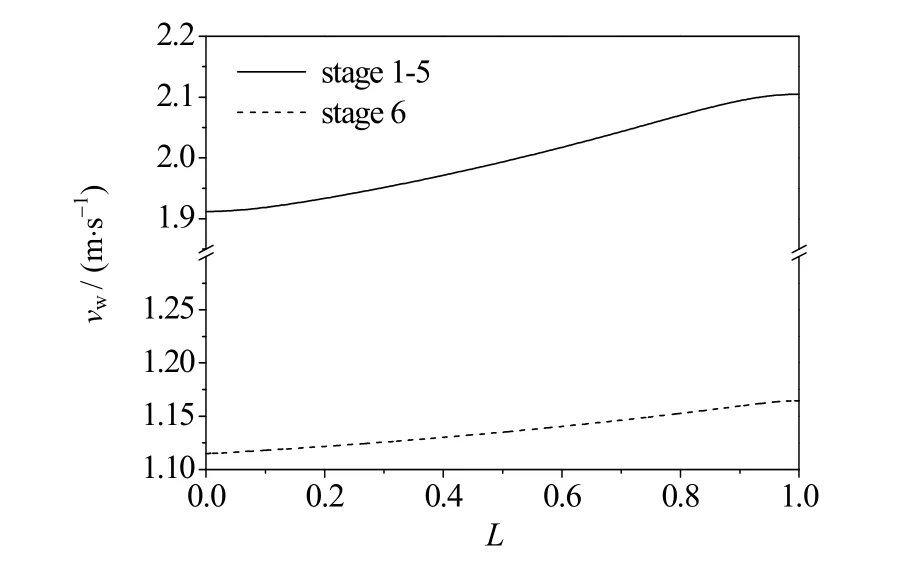
图8 床层渗流速度的轴向分布 Fig.8 Axial distribution of infiltration velocity

表5 稳态时操作条件及各段床层通道尺寸 Table 5 Steady state operation conditions and geometric parameters for each stage

表6 稳态时进出口及冷激进料组分 Table 6 Compositions of inlet, outlet and quenching feed under steady state

表7列出了Lurgi固定床反应器与多层径向床仿生反应器的一些性能的对比[31]。由表可见，对于多层径向床仿生反应器，采用中空圆柱型小颗粒催化剂后，不仅显著提高了催化剂有效系数ec，而且由于催化剂装填在具有分布式进出料的多层径向薄床层中，总压降并没有变大，与Lurgi固定床反应器的总压降值几乎相同(0.03 MPa)。此外，由于采用小颗粒催化剂，并在前五段床中限制了停留时间，从而有效抑制了副反应的发生，使得丙烯的最大选择性SC3H6提高了近7个百分点，并使单位催化剂质量的丙烯摩尔产率PM显著提高，提高了2.2倍；但是，由于多层径向床的通道结构需要占用相当一部分反应器体积，所以单位反应器体积的丙烯摩尔产率PV仅提高了17.6%。

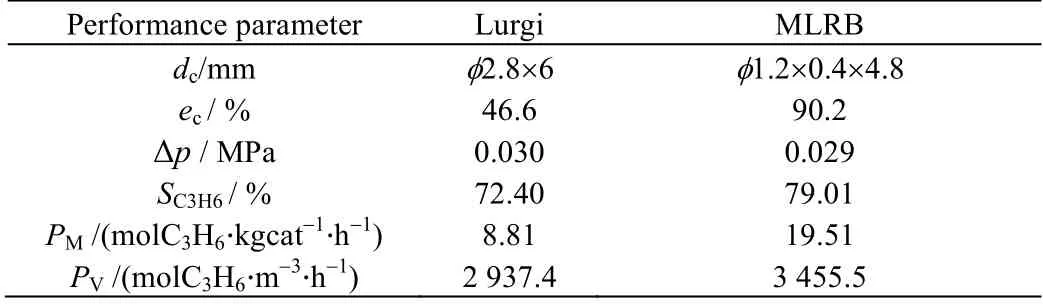
表7 Lurgi固定床[31]与多层径向床仿生反应器性能对比 Table 7 Performance comparison between MLRB and Lurgi fixed bed[31]

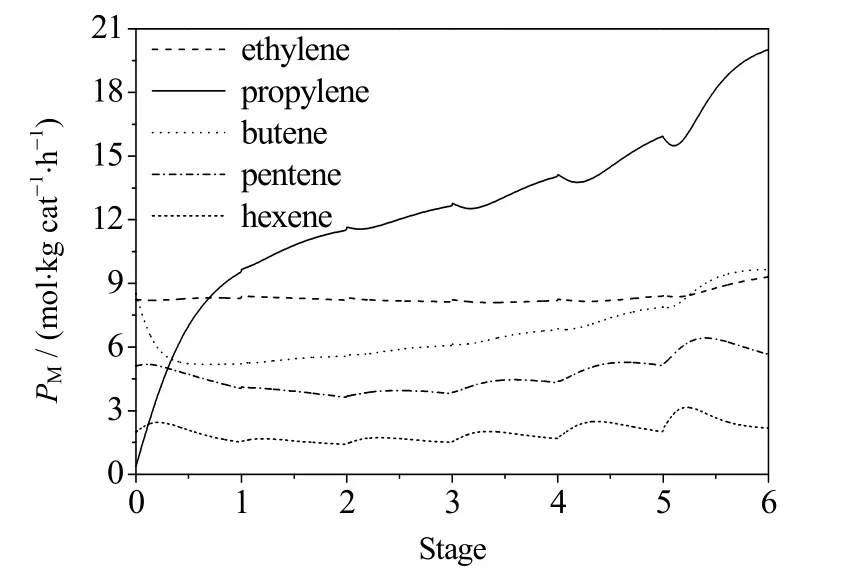
图9 稳态时六段床层中C2～C6烯烃组分的摩尔产率变化曲线 Fig.9 Profiles of molar productivity of C2-C6 olefins in each stage under steady state

4 结论

多层径向床作为仿生反应器的一种重要的实现形式，适合于大规模生产的快速气固相催化反应。其优点是压降低，可以装填高效的小颗粒催化剂，床层分布均匀，并且有解析解得到的函数关系式为尺寸优化设计提供可靠的理论依据。通过对MTP反应的案例研究，展示了多层径向床尺寸参数的设计及参数优化过程。模拟结果表明，与现有的Lurgi固定床相比，目标产物丙烯的最大选择性可以提高近7个百分点，并且达到相同的丙烯摩尔产率时催化剂的用量可以减少到原有的一半左右，体现出多层径向床仿生反应器在反应性能和经济性上的优势。

符号说明：

B — 床层渗透率，m2

C — 摩尔浓度，mol⋅m-3

Cp— 定压热容，J⋅kg-1⋅K-1

D — 扩散系数，m2⋅s-1

dc— 催化剂粒径，mm

ec— 催化剂有效系数

h — 通道半宽，cm

l — 通道高度，cm

L — 无量纲通道高度

p — 总压，MPa

Δp — 压差，MPa