基于能量密度等效的超弹性压入模型与双压试验方法1)

张希润 蔡力勋,2) 陈 辉

∗(西南交通大学力学与工程学院应用力学与结构安全四川省重点实验室,成都 610031)

†(长沙理工大学土木与工程学院,长沙 410114)

引言

超弹性材料广泛用于交通、建筑、机械、生物等工程领域,特别常用于结构的减震、密封等方面,其选材、工艺评价、老化分析都离不开表征材料基本性能的本构关系.超弹性材料的本构关系通常采用应变能密度与主伸长比之间的函数关系来描述[1-3].

1940 年代初,Treloar[4-5]通过构造三链分子网络模型,提出了表征应变能密度的Neo-Hookean 模型,该模型对橡胶拉伸应力−伸长比曲线的初始线性段有较为准确的描述,而因采用单参数,模型对曲线后继非线性段描述性较差.1940 年,Mooney[6]考虑代表性体积单元(representative volume element,RVE).RVE是连续介质力学的基本六面体单元,只要取合适的尺寸,就能用以求解受载构元的宏观力学行为)应变能密度与3 个主伸长比λi(i=1,2,3)之间的对称关系,提出了双参数超弹性材料本构关系.1948 年,Rivlin[7]利用材料RVE 变形张量不变量,根据材料体积不可压缩性,令第三不变量=1,则Mooney 本构方程可简化为连续介质力学框架下关于第一不变量I1和第二不变量I2的双参数方程形式

式中,C10和C01为材料参数,εi为主应变,该式称为Mooney-Rivlin 超弹性材料本构模型,该模型可较好描述小变形和中等程度大变形的超弹性本构关系,是迄今描述各向同性超弹性材料本构关系较为常用的模型.此外,Rivlin 为了拓展描述全程本构关系,还进一步提出了多参数的级数式本构模型.

材料压入试验法(压入法)是通过载荷或位移控制将压头压入材料并测得压入载荷P-压入深度h关系来获取材料力学性能指标的方法[8].压入法测试金属材料力学性能的方法主要包括:(1)Haggag[9-10]提出、Kwon[11]改进的多级加卸载自动球形压头压入(球压入) 方法,该方法对球压区平均应力进行表征修正获得压入试验过程中的多级表征应力σr和表征应变εr,通过这些数据可以回归获得Hollomon律参数; (2) Cao 等[12]提出的基于量纲分析和表征应力的半经验法,该方法通过量纲分析建立σr,h,P构成的无量纲项和比值σr/E∗(折减弹性模量) 之间关系的描述模型,该模型含有大量模型参数,须通过复杂流程方式迭代得到Hollomon 律参数; (3) Clyen等[13]提出的本构关系参数反向预测法,该方法基于大量材料本构关系参数关联的P-h压入曲线的FEA库与P-h压入试验曲线的相关性优化搜索以实现材料应力−应变关系的近似求解; (4)Cai 等[14-16]提出的半解析球压入方法,该方法根据能量密度中值原理获得的半解析压入模型和单球压入试验方法,通过金属宏观表面的P-h单级压入曲线实现了材料应力−应变关系、抗拉强度及布氏、洛氏、维氏硬度的仪器化测试.

对于超弹性材料,压入法测试材料力学性能的方法大多基于量纲分析法与搜索法.Zhang 等[17]采用与上述金属压入相似的量纲分析方法[12],对4 种广泛使用的超弹性材料本构模型,建立µ0(初始剪切模量)、R(压头半径)、h和P构成的无量纲项与本构模型参数、h和R构成的无量纲项之间的4 类关系模型,包含大量参数的这4 类模型均属于半经验性质,文献认为可通过试验获得与4 类模型参数相关的回归参量,并未通过球压入实现本构关系的反向求解.Pan 等[18]主要结合多级应变能密度函数的Ogden 超弹性本构模型,通过对球、平面、锥3 类压头压入(球压入、平面压入、锥压入)问题进行量纲分析,证明了单类单压头无法独立实现多参数超弹性本构模型的参数求解,同时证明了单类单压头可实现单参数超弹性本构模型求解的唯一性,但作者未给出超弹性压入问题的具体求解方法.Giannakopoulos 等[19]基于Mooney-Rivlin 模型获得了球压入比值h/R小于0.1 情况下P-h压入曲线的解析解,并未由此获得本构关系,Giannakopoulos 认为通过单球压入不能唯一性获得本构模型参数.Chen 等[20]对一种硅橡胶进行球压入试验,利用Oliver 和Pharr 法[21]获得材料的弹性模量,并对Neo-Hookean、Mooney-Rivlin、Yeoh三类超弹性本构模型,通过调整模型参数进行P-h压入曲线的有限元分析,以此逐渐逼近P-h压入试验曲线,进而反向求解获得本构模型参数.Saux 等[22]采用半锥角70.3◦的圆锥形压头对天然橡胶完成锥压入试验,并设定材料参数初值后进行了有限元计算,将有限元计算结果与P-h压入曲线之间的误差作为目标进行基于最小二乘法的迭代计算,取两者误差最小时所设定的材料参数为本构模型的参数.Lee 等[23]以Yeoh 模型作为橡胶的本构模型,将P-h球压入试验曲线映射为应变能密度与I1关系曲线,以该曲线确定模型参数,并与给定初值进行比较,误差最小时即为模型参数.Song 等[24]对不同参数的Yeoh 模型进行球压入有限元模拟,建立了压入载荷−位移曲线数据库,并采用与Yeoh 模型参数相关的三次多项式对载荷−位移曲线回归分析得到本构模型参数.

关于超弹性材料的压入法多属于经验或半经验性质,至今尚无公认的、得到大量试验验证的成熟方法.本文基于能量密度中值等效原理[25-26],提出描述P、h和Mooney-Rivlin 模型参数之间关系的半解析超弹性压入模型并进行有限元正反向验证,进而提出用于测试超弹性材料本构关系的压入试验方法,并对3 种橡胶材料进行压入试验,将压入试验获得的本构关系结果与拉伸试验结果进行比对验证.

1 半解析超弹性压入模型SHIM

1.1 Mooney-Rivlin 模型的应力应变形式

在复杂应力应变条件下,超弹性材料的应力应变关系由第二Piola-Kirchhoff 应力σij和Green 应变εi j来表示为

式中I1,I2,I3为变形张量的3 个不变量.对于各向同性、不可压缩超弹性材料,=1,根据第二Piola-Kirchhoff 应力与Cauchy 应力之间关系[27-28],可得主应力τi与主伸长比λi之间的关系为

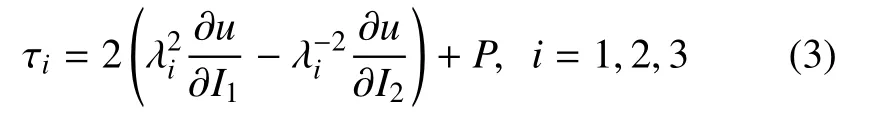
式中,P为静水压力.由于主伸长比λi与主应变εi指数关联,故式(3)表征了RVE 的应力−应变关系.

对于Mooney-Rivlin 超弹性材料本构模型,式(4) 可写为

由真应力τ 与工程应力σg关系:τ=λσg,令λ1=λ,τ1=τ,则由式(5)可得

式中,λ=eε通过单轴拉伸试验获取被测材料的σg–λ曲线,将σg/[2(λ −λ2)]作为纵坐标,λ−1作为横坐标做出两者关系曲线并进行线性回归,则截距和斜率分别为Mooney-Rivlin 模型的两个参数:C10和C01.

1.2 基于能量密度等效方法的半解析压入模型

由积分中值定理,受载固体的有效变形域Ω 内必存在一点M,在M处RVE 的应变能密度uM与Ω域的平均应变能密度相等,即

式中,U为变形域的总应变能,Veff为有效变形域体积,则按Mooney-Rivlin 模型,M点处RVE 的应变能密度表为

由式(7)和式(8)可得

以特征体积D3使上式有效体积无量纲化,则上式可化为

式中,特征长度D在球压入时取为压头直径,平面压入时取为圆柱压头直径,锥压入时D取为特征压入深度hc.假设无量纲变形量f1,f2与无量纲位移h/D之间满足幂律关系,即

且假设变形系数k1,k2及变形指数k0均为与压入的压头类型相关但与材料无关的常数.将f1,f2的表达式代入式(10)可得

对于压入问题,由能量守恒可得

式中W为外力功.结合式(12)和式(13),以h对U求导,并无量纲化,可得P与h的关系

式中加载指数k0为与加载方式相关、与材料无关的常数,加载系数C为与材料和加载方式相关的常数.该式称为半解析超弹性压入模型SHIM (semitheoretical hyperelastic-material indentation model).

基于式(14),由单压头的P-h压入曲线可回归得到加载系数C,Mooney-Rivlin 模型的双参数C10和C01仅由独立的C值无法求解.须根据两种不同类型压头的P-h压入曲线通过以下两式

实现Mooney-Rivlin 模型的双参数C10和C01求解.式(15)中C与C′分别对应两种压头的P-h压入曲线的加载系数.

1.3 k0, k1, k2 的有限元确定方法

幂律方程式(11)的系数k1,k2和指数k0均为与压头类型相关的常数,可通过FEA 确定.由于式(14)为无量纲方程,故针对球压头、圆柱平面压头可选择特定压头尺寸以及针对锥压头选择特定角度进行压入变形分析.选定球压头、圆柱平面压头直径均为2 mm,以及特征压入深度hc为0.8 mm 时半锥角分别为53◦,60◦,65◦,70.3◦,75◦锥压头进行有限元分析确定k0,k1,k2.

假设受压试样的材料本构关系符合 Mooney-Rivlin 模型律,应用有限元分析软件Ansys14.5 对如图2 所示的球、平面、锥压入的轴对称网格模型完成有限元计算.Mooney-Rivlin 模型参数C10和C01取值分别满足C10∈(0.01,2)MPa 和C01∈(0.1,2)MPa,网格模型采用Plane 182 平面单元,试样的受压接触面使用Contact 172 接触单元,并在接触区域采用高密度网格,而在离接触区域稍远处用较低密度网格.

图1 有限元轴对称模型Fig.1 The axisymmetric FEA indentation model

对符合C10∈(0.01,2) MPa 的C10分别取0.01,0.1,0.5,1,1.5,2 MPa 及符合C01∈(0.1,2) MPa 的C01分别取0.1,0.5,1,1.5,2 MPa,共计30 种材料进行FEA 计算得到3 类压入下的P-h压入曲线,通过式(14)分别确定C,得到球、平面、锥3 类压入下的3 组方程,进而通过简单回归可得到球、平面压入下SHIM 参数k0,k1和k2如表1 所示,特征压入深度hc为0.8 mm 时不同角度锥压入下SHIM 参数k0,k1和k2如表2 所示.

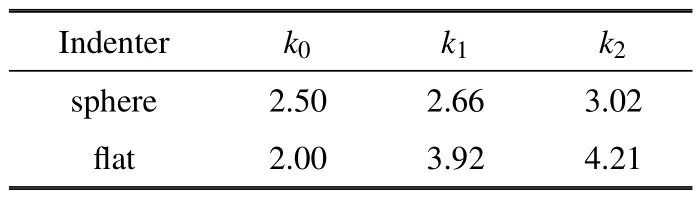
表1 球压入与平面压入下SHIM 参数Table 1 Parameters of SHIM for spherical and flat indentation

表2 锥压入下SHIM 参数Table 2 Parameters of SHIM for conical indentation

由表1 可见,k0是规则的常数,特别在平面压入下k0=2,即P-h压入曲线呈线性; 对于球压入及平面压入,SHIM 参数与直径无关.

由表2,对于锥压入,不同半锥角下SHIM 变形系数k1,k2不同,但变形指数k0均为3,即锥压入P-h关系符合抛物律.图2 表明,k1,k2与半锥角余弦值cosθ 关系之间符合幂律

式中,系数β11,β21和指数β12,β22由表3 给出.

图2 变形系数k1,k2 随cosθ 的变化曲线Fig.2 Variations of deformation coefficient k1,k2 with cosθ

表3 变形系数kTable 3 Deformation coefficient k

2 有限元验证

2.1 向验证:压入载荷−深度关系比对

对1.3 节计算中采用的30 种材料本构关系参数,可通过SHIM 预测得到材料分别在3 类压头压入下的P-h压入曲线,图3 示出了SHIM 预测的P/P*-h/D压入曲线与FEA 分析曲线,可见30 种材料条件下两者之间密切吻合,SHIM 有很好的P-h压入曲线预测精度,并有很强的材料普适性.

图3 预测P-h 压入曲线与FEA 结果比较Fig.3 Comparisons of predicted P-h indentation curves and those from FEA

2.2 反向验证:应力−伸长比关系比对

对1.3 节的30 种材料FEA 分析得到的球、平面、锥压入下P-h压入曲线,通过3 类压头两两组合压入的方式,由式(15)分别得到3 组加载系数:C,C′,进而可分别求得3 组Mooney-Rivlin 模型参数:C10,C01,再根据式(6) 分别得到3 组本构关系曲线(应力−伸长比曲线).图4 示出了预测的3 组本构关系曲线与FEA 条件曲线,可见30 种材料条件下各类预测曲线之间、与FEA 条件曲线之间均密切吻合,SHIM 有很好的单轴本构关系预测精度.

图4 预测应力−伸长比关系与FEA 结果比较Fig.4 Comparisons of predicted stress-stretch ratio curves and the FEA results

3 试验方法与验证

3.1 拉伸与压入条件

对天然橡胶(NR)、氯丁橡胶(CR)、丁基橡胶(IIR) 进行单轴拉伸试验并进行球、平面、锥压入试验.

基于国家标准GB/T 528—2009[29]对3 种橡胶材料进行单轴拉伸试验如图5 所示,采用标准裁刀将购置的2 mm 厚橡胶板加工成标准哑铃状试样,采用CARE 原位双向拉压试验机以2 mm/s 加载速率完成单轴拉伸试验.

图5 单轴拉伸试验装置Fig.5 Uniaxial tension test equipment

采用图 6 所示的 IMTSC型压入仪完成压入试验,压头分别选取直径 2 mm 球形及圆柱形平面压头和半锥角 70.3◦锥形压头,试样尺寸40 mm×40 mm×30 mm,试验加载速率为3µm/s[30],3 类压头的最大压入深度h均为0.8 mm,每种材料试样进行两次单压头压入试验.

图6 压入试验装置Fig.6 Indentation test equipment

3.2 双压试验方法与试验比对

由式(14),对球、平面、锥单压头压入下的P-h试验曲线进行回归可得加载系数CS、CC、CF,进而可得它们关于Mooney-Rivlin 模型双参数C10和C01的表达式

对式(17) 中3 个方程任意两两组合,即可求解C10和C01; 此外,不同半锥角条件下也可形成两组独立的加载系数求解方程.由球、平面、锥单压头压入两两组合及不同半锥角下的锥−锥压头压入下获取Mooney-Rivlin 模型参数的试验方法统称为双压试验方法(indentation method due to dual indenters,IMDI).此外,不同直径的双球压头压入或双圆柱平面压头压入因k1,k2不随压头直径变化的自相似性,而不能采用同类压头压入配对方式获得材料本构关系.

图7 给出了3 种材料的单轴拉伸载荷P-位移l试验曲线,由单轴拉伸条件下伸长比λ 和应力σ 的定义

可求出拉伸过程中λ 和σ 的试验数据.式(18)中l0为试样原长,l为拉伸试样等直段位移.图8 给出了应力−伸长比曲线.

图7 单轴拉伸载荷−位移曲线Fig.7 Uniaxial tension load-displacement curve

图8 单轴应力−伸长比曲线Fig.8 Uniaxial stress-stretch ratio curve

图9 压入载荷−深度曲线Fig.9 Indentation load-depth curve

图9 示出了球、平面、锥压头独立压入试验下3 种材料的P-h压入试验曲线,对获得的P-h压入试验曲线进行幂律回归,为消除系统误差,平移P-h压入试验曲线,直至回归的P-h压入试验曲线的指数k0与表1 或表2 中的k0相同.针对P/P∗−h/D试验曲线,球压入时选h/D∈[0.15,0.4]数据段、平面压入时选h/D∈[0.1,0.4] 数据段、锥压入时选h/D∈[0.15,0.4]数据段进行回归分别得到加载系数CS,CF,CC.

图10 给出了使用双压试验方法IMDI 对球、平面、锥压入两两结合预测的材料本构关系及单轴拉伸试验结果,可见IMDI 预测超弹性材料本构关系之间及与单轴拉伸试验结果之间均吻合良好.

图10 预测应力−伸长比关系曲线与单轴拉伸结果对比Fig.10 Comparison between predicted stress-stretch ratio curve with the uniaxial tensile results

4 结论

(1)基于能量密度等效原理,提出了球、平面、锥3 类压头独立压入条件下,描述载荷、深度、Mooney-Rivlin 关系参数、几何尺寸之间关系的压入模型SHIM,SHIM 正向预测的P/P∗−h/D压入曲线与FEA分析曲线之间密切吻合;球、平面、锥压头两两组合压入下SHIM 反向预测的3 组本构关系曲线之间及与FEA 条件本构关系曲线之间均密切吻合.

(2) 提出了由球、平面、锥单压头两两组合压入下及具有不同半锥角的双锥压头压入下获取Mooney-Rivlin 模型参数的双压试验方法.

(3) 对3 种橡胶材料分别进行单轴拉伸试验及球、平面、锥压入试验,结果表明,通过双压试验方法预测得到的本构关系曲线均与单轴拉伸试验结果具有良好的一致性.