基于VMD-PARAFAC的轴承故障欠定盲源分离*
2020-06-10李志农杨晓飞陈长征
李志农,杨晓飞,陈长征
(1.南昌航空大学 无损检测教育部重点实验室,南昌 330063;2.沈阳工业大学 机械工程学院,沈阳 110870)
在机械设备故障监测中,盲源分离是一种有效的信号处理方法,在源信号和传递路径未知的情况下,仅对观测信号处理即可估计出源信号,因此,盲源分离思想在故障诊断领域中得到了广泛应用.Haile等[1]将BSS方法应用在旋转机翼的故障特征提取中;Elia等[2]将BSS方法与循环平稳方法结合起来对变速箱中轴承的磨损情况进行监测;Araujo等[3]将BSS方法与传递函数结合起来对振动系统的模态参数进行识别;周昊等[4]提出了一种基于粒子群优化算法的盲源分离方法,用于提取风机主轴承故障信号特征,取得了良好的诊断效果;席剑辉等[5]提出一种基于联合近似对角化和独立分量分析的盲源分离方法,实现对轴承故障声发射信号的分离.
但是在多数情况下,由于受到硬件成本和空间的限制,系统中只能安装一个传感器,传感器个数小于源信号个数,即为欠定盲源分离,因此,研究单通道复合故障的分离方法更具有广泛的现实意义.李志农等[6]结合小波分析和核典型相关分析(KCCA)各自的特点,提出一种基于小波-KCCA非线性欠定盲源分离方法;Wang等[7]提出了一种基于EEMD和ICA的欠定盲源分离方法,成功地对轴承故障信号进行分离.但是,EEMD会导致计算量的增加,同时也无法应用于嘈杂的工业环境.VMD[8]的出现为故障特征提取提供了新的机遇,VMD可以非递归地将多分量信号分解为多个带限本征模态函数,从而提高效率.同时滚动轴承的振动信号频率正好受频带限制,带宽受限的先验信息可确保在嘈杂的环境中保持高效.Tang等[9]将VMD和ICA相结合来解决轴承复合故障的欠定盲源分离问题.首先采用VMD算法对单通道的复合信号进行分解,得到若干BLIMFs,然后将这些BLIMFs作为输入矩阵,采用ICA算法对故障信号进行分离.
传统方法主要采用模态分解方法(如经验模态分解、集合经验模态分解以及变分模态分解等),对单通道的观测信号进行分解,得到若干子信号分量,然后将其作为新的输入信号,采用ICA算法或其改进算法对新的观测信号进行分解,从而分离出故障源信号.ICA算法是基于矩阵的分解,通常需要施加一些约束条件,如正交性、独立性和恒模特性等才能保证分解的唯一性.在实际工程中,很难满足这些苛刻的条件,导致矩阵分解的非唯一性,以致很难保证盲源分离结果的准确性.
PARAFAC是一种基于张量的分解方法,在宽松条件下可以实现分解的唯一性[10],因此,本文结合VMD和PARAFAC的各自优点,提出一种基于VMD-PARAFAC的轴承复合故障欠定盲源分离方法.同时,将提出方法与传统的基于VMD-ICA的故障盲源分离方法进行对比分析,以此验证所提方法的有效性.
1 欠定盲源分离
盲源分离方法能够在源信号以及传输通道参数未知的情况下,仅根据输入信号的统计特性即可从观测信号中恢复源信号,其计算过程可以表示为
X(t)=AS(t)+E(t)
(1)
式中:S(t)=[s1(t),s2(t),…,sM(t)]T为M个源信号;X(t)=[x1(t),x2(t),…,xN(t)]T为N个观测信号;A为M×N维混合矩阵;E(t)为误差.
因为源信号及混合矩阵的先验知识未知,所以必须做出如下假设:1)源信号在统计上彼此独立;2)混合矩阵A是列满秩矩阵;3)源信号数M小于或等于观测信号数N.
在实际工程中,为解决多故障的欠定盲源分离问题,首先采用VMD算法对观测信号分解,得到若干BLIMFs,将欠定盲源分离转化为非欠定盲源分离,然后将BLIMFs矩阵构造成三阶张量形式作为PARAFAC模型的输入,最后采用三线性交替最小二乘(trilinear alternating least squares,TALS)算法[11]对PARAFAC模型进行拟合,得到混合矩阵的估计,进而得到解混合矩阵和源信号估计.
2 VMD-PARAFAC模型建立
2.1 VMD算法
VMD是自适应信号分解的时频分析方法,可以通过特殊变分模型的迭代求解将多分量信号分解为多个BLIMFs.
观测信号X(t)可以分解为有限数量的子信号uk,每个子信号有不同的中心频率ωk和有限带宽.首先通过希尔伯特变换获得uk的单边频谱,即
(2)
式中:δ(t)为狄利克雷函数;*为卷积运算.
通过混频将每种模式的频谱转移到基带中,即
(3)
接下来,可以通过对式(3)中解调信号的L2范数估计每个模态的带宽.最后,将VMD构建为约束变分模型,即
(4)
式中,{uk}={u1,u2,…,uk}和{ωk}={ω1,ω2,…,ωk}分别为每个模态和模态对应的中心频率.
为了获得上述变分模态的最优解,引入二次惩罚因子α和拉格朗日乘数λ(t)到VMD中,使上述限制性问题转化为非限制性问题的求解,即
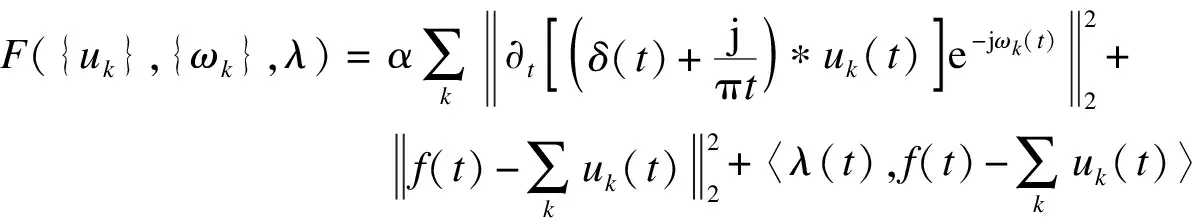
对于竖缝式鱼道而言,在确定池室细部结构时,不仅要考察水流流态与流速分布,还要关注各级鱼室内的能量耗散情况。如果鱼室参数设计不合理,水流消能不够充分,容易导致鱼类消耗大量的体力,不能顺利上溯。法国的Larinier[5]对竖缝式鱼道的消能效率进行了深入研究,提出单位消能率的概念,并给出了各级水池内的单位水体消能率E不得超过150~200 W/m3的建议。因此,对池室内单位水体消能率进行计算是必要的。
(5)
使用方向交替乘子算法[12]迭代交替更新{uk}、{ωk}、λ.
2.2 PARAFAC模型
将上述得到的分量uk构造新的观测信号Z(t),把Z(t)分成不重叠的L段数据块,每段包含Nl=K/L个数据点,用l=1,2,…,L表示数据块的个数,则观测信号可表示为
Z(l,t)=WS(l,t)+E(l,t)
(6)
式中:Z(l,t)=[z1(l,t),z2(l,t),…,zN(l,t)]T为新的观测信号;W为白化矩阵.
每段观测信号的协方差矩阵RZ可表示为
RZ(Tl)=WRS(Tl)WT
(7)
式中,RS为源时滞协方差M×M阶矩阵.
假设源信号S(t)=[s1(t),s2(t),…,sM(t)]T之间互不相关,则RS为对角阵.将每段观测信号的协方差矩阵RZ(Tl)叠加在一起,构成三阶张量形式,记为Rn1,n2,l,其中,n1=1,2,…,N,n2=1,2,…,N,l=1,2,…,L.W中的元素记为wn×m,构建一个M×L维矩阵C,其表达式为
(8)
由式(7)可得
Rn1,n2,l=Wdiag(C)WT
(9)
(10)
通过TALS算法对张量Rn1,n2,l分解,得到矩阵W,进而估计出源信号.VMD-PARAFAC算法的流程图如图1所示.
3 仿真分析
为验证所提方法的有效性,构造一组仿真信号来模拟轴承复合故障信号,故障频率设为50和90 Hz,仿真源信号可表示为
(11)
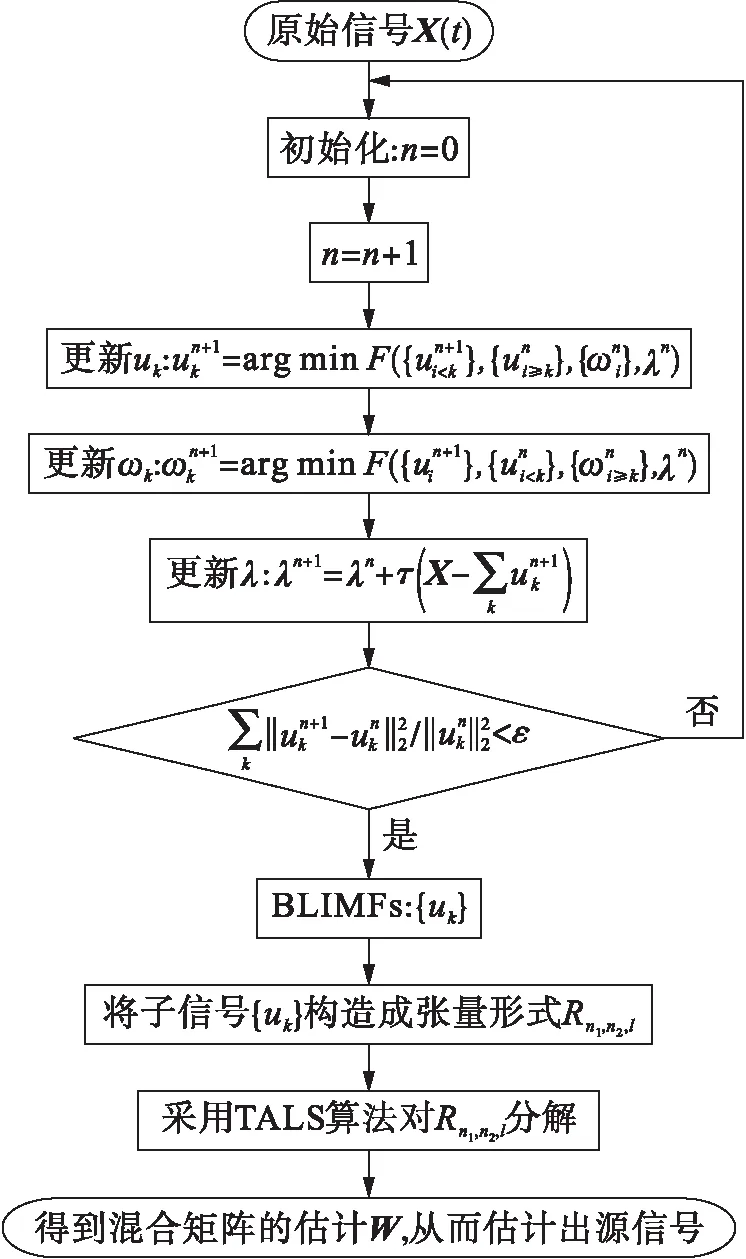
图1 VMD-PARAFAC算法流程图
为了得到虚拟观测信号,选择一个随机矩阵A=[0.859,0.461],根据X(t)=AS(t)得到一组观测信号,再对观测信号添加20 dB的噪声.采样频率设为2 000 Hz,采样点数为2 000,则观测信号的时域波形和频谱如图2、3所示.从图3可以看出,观测信号的频谱中包含了50和90 Hz的故障特征频率,说明两个仿真故障源信号完全混叠在一起,无法准确判断故障类型.
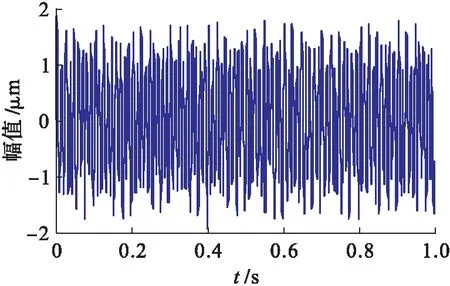
图2 仿真信号的波形
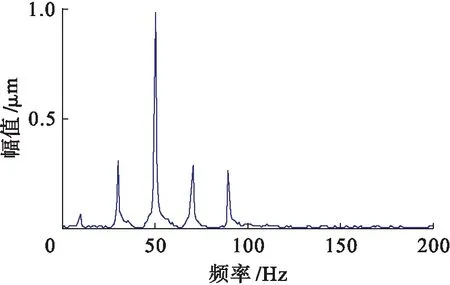
图3 仿真信号的频谱
用传统的VMD-ICA方法和所提VMD-PARAFAC方法分别对观测信号进行处理,得到估计信号的频谱图如图4、5所示.从图4可以看出,两个仿真故障源信号完全混叠在一起,采用VMD-ICA方法没有达到良好的分离效果.但是,从图5可以清楚地看到,两个混叠的故障信号被分离出来,故障特征频率与设定的完全相同,充分证明了所提方法的有效性.

图4 仿真估计信号的频谱(VMD-ICA)
4 实验研究
实验所用数据采自北京化工大学,实验装置如图6所示.主加速度传感器安装在轴承箱的顶部和侧面,获得2个通道的振动信号.以轴承外圈-滚动体的复合故障为研究对象,根据文献[9]给定的轴承参数和转频可以计算出外圈和滚动体各自的故障频率,分别为86.3和102.3 Hz.实验采样频率设为100 kHz,选取一组传感器数据中的50 000个点作为实验数据.图7、8分别为观测信号的波形和频谱.
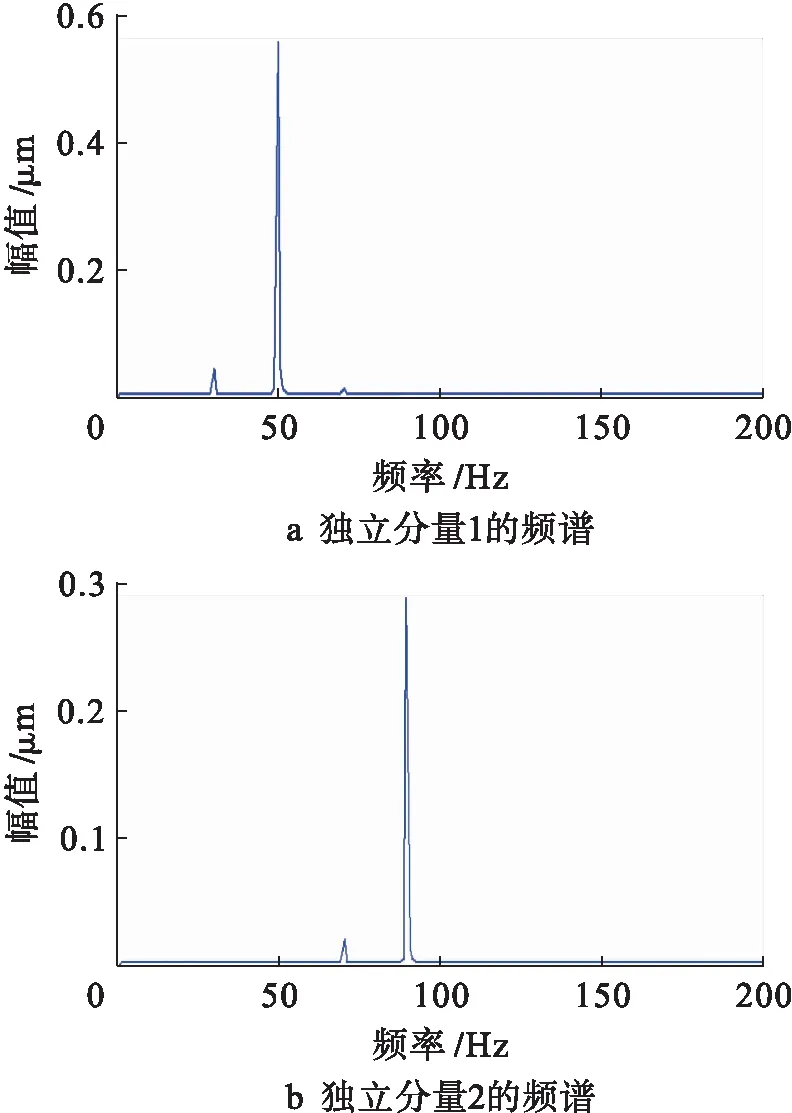
图5 仿真估计信号的频谱(VMD-PARAFAC)

图6 实验系统和传感器的位置
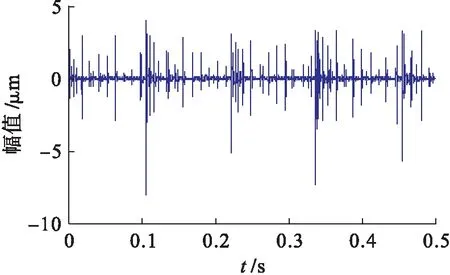
图7 观测信号的波形
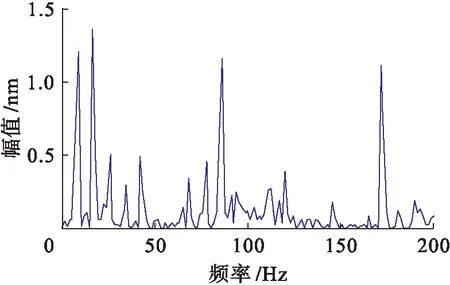
图8 观测信号的频谱
从图8仅能看出外圈的故障特征频率为86.9 Hz,滚动体故障特征频率被完全掩盖,无法看出滚动体的故障特征频率.
采用基于VMD-ICA的盲源分离方法和VMD-PARAFAC的盲源分离方法对观测信号进行处理,估计信号的频谱分别如图9、10所示.根据图9可以看出,外圈故障特征频率为86.9 Hz,与理论计算的特征频率一致.滚动体的故障特征频率为94.6 Hz,与理论计算的故障特征频率相差较大,无法看出滚动体的故障特征.根据图10可以看出,外圈故障特征频率为86.9 Hz,刚好对应理论计算的特征频率,滚动体的故障特征频率为100.7 Hz,与理论计算的故障特征频率102.3 Hz有一点偏差,可能与轴承滑动和安装误差有关.但也能充分说明所提方法能够对轴承外圈-滚动体复合故障信号进行分离.
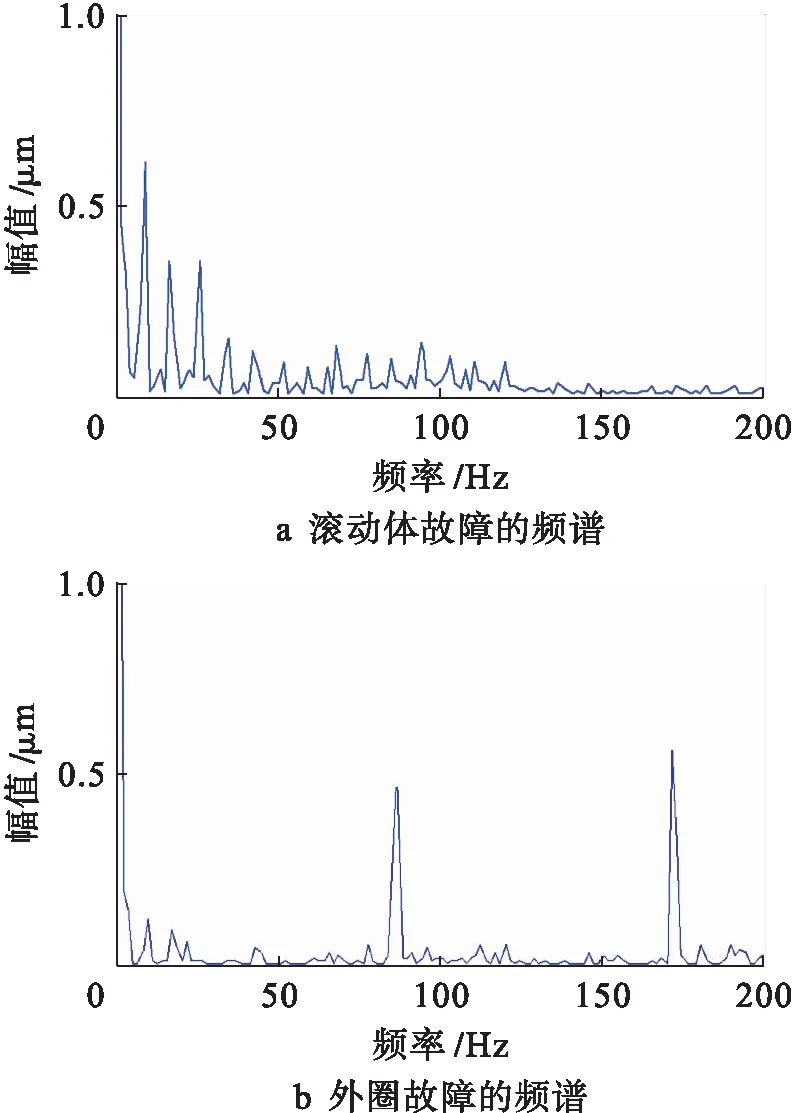
图9 估计信号的频谱(VMD-ICA)
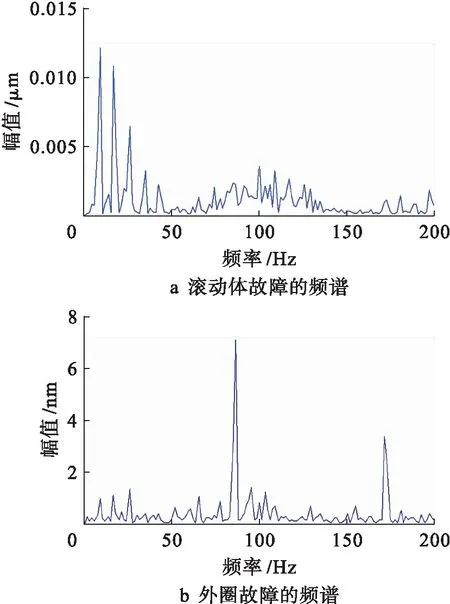
图10 估计信号的频谱(VMD-PARAFAC)
5 结 论
通过上述分析可以得出以下结论:
1)基于平行因子分解唯一性的独特优势,将PARAFAC与VMD结合起来,应用到轴承外圈-滚动体复合故障欠定盲源分离中.该方法首先采用VMD算法对观测信号分解,得到多个BLIMFs分量,然后将这些分量矩阵构造成张量形式,作为PARAFAC算法的输入,最后采用TALS算法对PARAFAC模型进行拟合,得到混合矩阵估计,从而估计出源信号.
2)所提方法与传统的VMD-ICA盲源分离方法进行了对比分析,仿真和实验分析也证明该方法具有实用价值.
