基于共模电压抑制的六相电机空间矢量调制*

张志锋，叶思聪

(沈阳工业大学 电气工程学院，沈阳 110870)

近年来，多相永磁电机因其具有低压大功率输出，转矩脉动小，系统动、静态性能优秀，可靠性和容错性高等特点备受关注[1-3].双Y移30°六相电机是多相电机应用较多的一种，具有良好的发展前景.

双Y移30°六相电机的定子有两套中性点相互独立的三相星形绕组，互相之间相差30°.由于电机的交流调速系统普遍采用PWM脉宽调制技术，这会导致共模电压的产生，该共模电压可以用定子绕组的中性点与逆变器直流母线中点之间的电压来衡量[4].在寄生电容的作用下，共模电压会成为电磁干扰和轴电压的重要来源，可能使轴承油膜击穿形成轴电流，导致电机轴承损坏.抑制共模电压的方法主要集中于电机结构的设计，逆变器结构的改善，调制算法的优化以及采用有源、无源滤波器滤波[5-9].此类方法虽然能在一定程度上抑制共模电压，但是效果欠佳，局限性比较大.而采用合成中间矢量的办法抑制共模电压会带来电力电子器件开关频率过高，直流母线电压利用率过低等问题.

为此，本文对双Y移30°六相电机共模电压进行分析，提出一种新型抑制共模电压的空间矢量调制方法，既能抑制共模电压的峰值大小和变化频率，又具有良好的电流、转矩和转速性能，同时保证了较高的直流母线电压利用率和较低的电力电子器件开关频率，并进一步通过仿真验证其性能.

1 六相电机的VSD变换与共模电压

双Y移30°六相电机与两电平电压型逆变器组成的系统如图1所示，其中第一套绕组(ABC绕组)与第二套绕组(DEF绕组)相差30°，中性点(N，N′)相互独立且与逆变器直流母线侧中点g相互独立.绕组中性点与直流母线中点之间的电压UNg与UN′g即为共模电压，其表达式为

(1)

逆变器共有六个桥臂，每个桥臂的上下两个开关器件都工作在互补导通状态，故每个桥臂有两个工作状态，整个逆变器有26=64个开关状态.通过空间矢量解耦变换[10]，与转换开关相对应的64种基本电压矢量表示为

(2)

式中：Uαβ、Uz1z2、Uo1o2分别为电压矢量在三个相互正交的子平面内的分量；α=ej30°；s为每个桥臂的开关状态，s=1为上桥臂导通，s=0为下桥臂导通.另外，式(2)还可以变换为

(3)

式中，*为共轭.这样就可以将这64种状态映射到三个相互正交的子平面，即α-β子平面(含有基波分量以及12k±1次谐波分量，k=1，2，3，…)，z1-z2子平面(含有6k±1次谐波分量，k=1，3，5，…)以及o1-o2子平面(含有6k±3次谐波分量，k=1，3，5，…).α-β子平面和z1-z2子平面的基本电压矢量分布如图2所示，矢量的编号为八进制数，对应二进制的六个桥臂开关状态，1为上桥臂导通，0为下桥臂导通，顺序为ABCDEF.其中矢量00，07，70，77在所有子平面均为零矢量.

根据式(1)可以计算出各个基本电压矢量的共模电压UNg与UN′g，并根据数值将其分类，具体情况如表1所示.当某一组桥臂处于零功率状态时，共模电压峰值都会很大，所以应避免使用这些电压矢量尤其是四个零矢量.而用其他电压矢量合成零矢量并利用传统控制方法控制时，不可避免地会使电力电子器件的开关频率激增，这很不利.

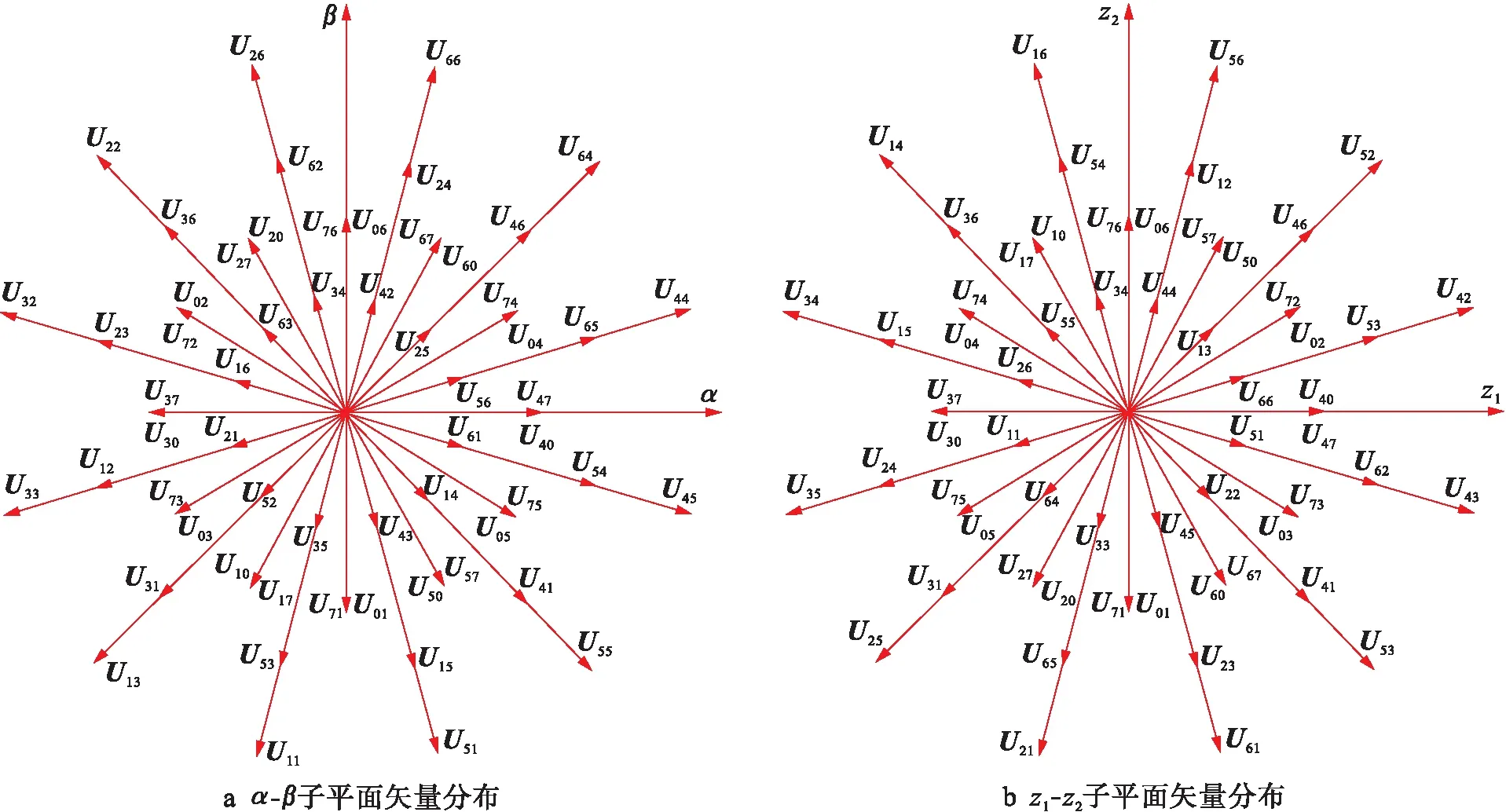
图2 基本电压矢量分布

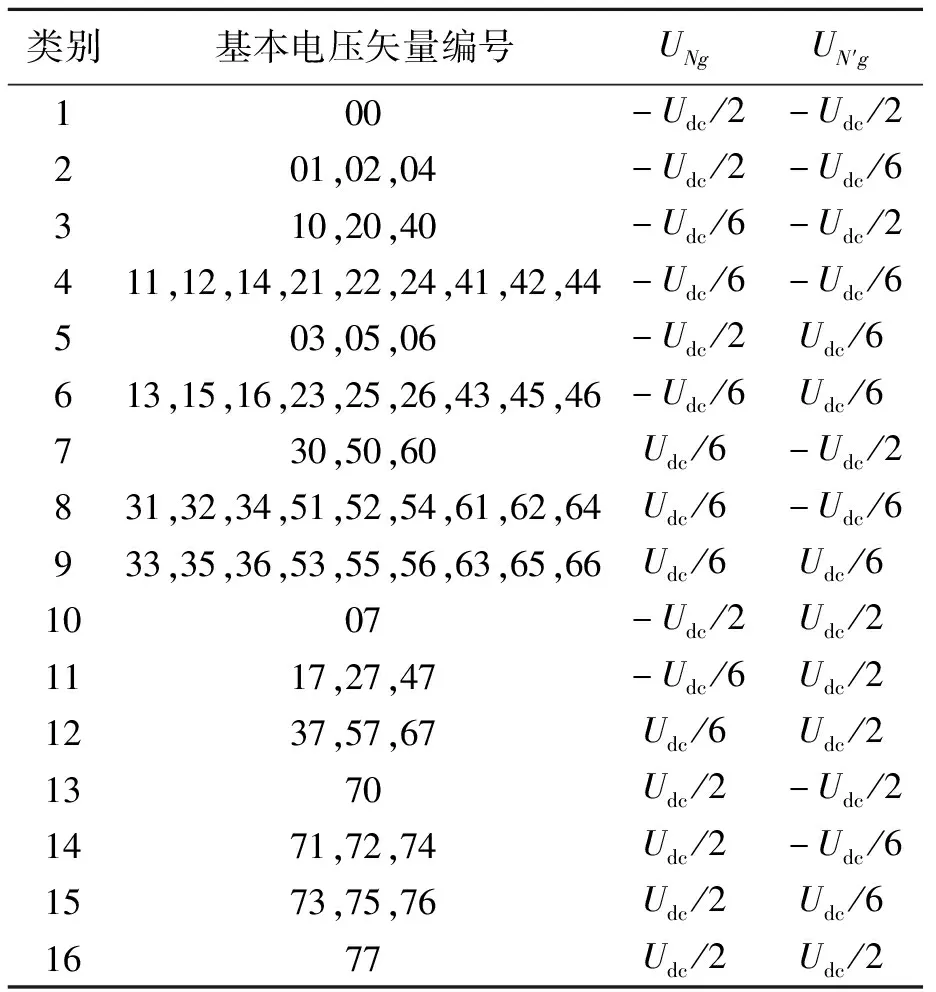
表1 各基本电压矢量共模电压幅值

本文通过三相解耦算法将六相电压源逆变器的电压矢量分解到两个三相电压源逆变器中，再利用无零矢量PWM调制分别合成新型调制方法.此方法既能有效降低共模电压的幅值和变化频率，也具有良好的电流、转矩和转速性能.

2 三相解耦算法及无零矢量调制

2.1 三相解耦算法

三相解耦PWM算法[11]将六相电压源逆变器的电压矢量分解成两个三相电压源逆变器中的电压矢量，然后用三相电机的控制方法进行控制.

六相逆变器可以看成由两个三相逆变器1和2组成，开关状态对应关系为

(4)

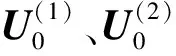
(5)

(6)

把式(4)～(6)代入式(2)中，经过变换，六相逆变器中的基本电压矢量和两组三相逆变器电压矢量间的关系表示为

(7)

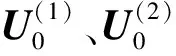
(8)

由于中性点独立，不会有零序电流产生，可以忽略零序分量.两个三相逆变器输出的参考电压矢量U1ref和U2ref可以替代由六相逆变器输出的α-β子平面和z1-z2子平面参考电压矢量Uαβref和Uz1z2ref，即

(9)

由于z1-z2子平面的电流只有谐波分量，不会产生电磁转矩，所以需要z1-z2子平面参考电压矢量为0，两个三相逆变器输出的参考电压矢量U1ref和U2ref为

(10)

两个三相逆变器输出参考电压矢量之间的关系如图3所示.

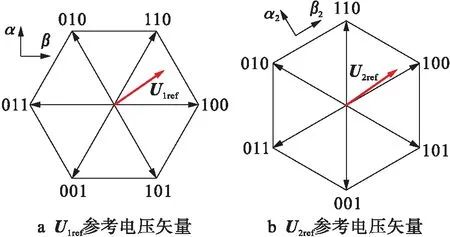
图3 两个三相逆变器的参考电压矢量

2.2 三相解耦控制方法的电压利用率

三相空间矢量控制方法的直流电压利用率取决于基本电压矢量六边形的内切圆半径，输出的电压极限约为0.577Udc，三相解耦控制方法的两个三相逆变器也遵循此原理.两个三相逆变器输出的电压极限如图4所示，两个基本电压矢量六边形大小相同，中心重合，故内切圆半径也相同，所以此方法输出的电压极限为0.577Udc，电压利用率与传统的四矢量空间矢量调制方法相同.

2.3 三相无零矢量PWM调制方法

三相电机的空间矢量控制无论是采用七段式还是五段式算法，都要使用两个相邻的基本电压矢量和零矢量，故共模电压峰值很大，如图5a所示.本文采用相对基本电压矢量合成零矢量的方法取代零矢量[12]，为降低电力电子器件的开关频率，使用两个相邻的基本电压矢量中的一个及其相对的基本电压矢量，如图5b所示.

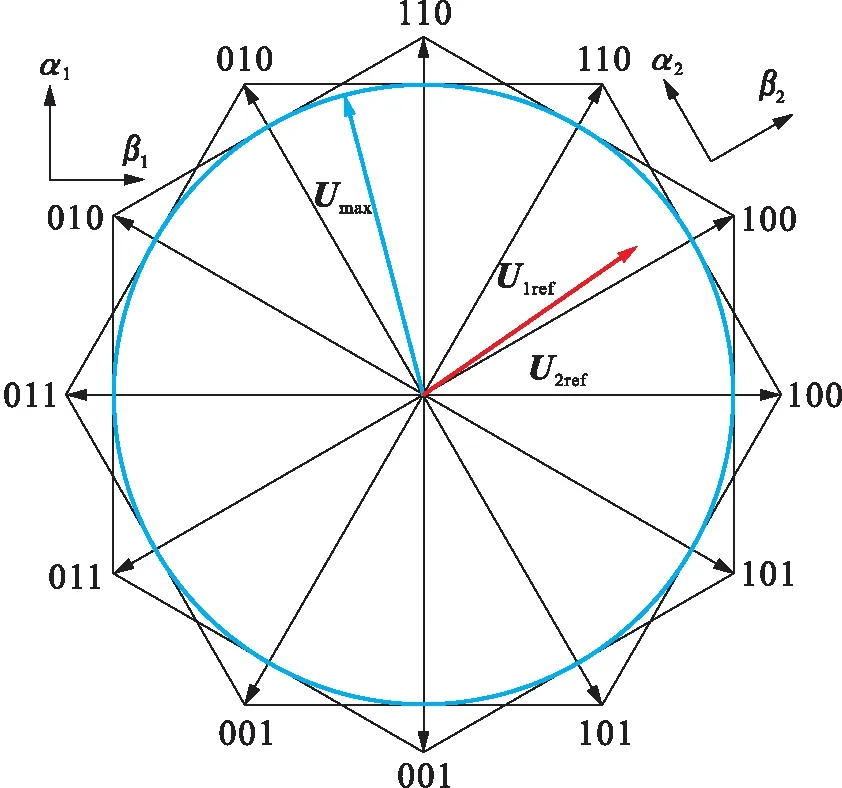
图4 两个三相逆变器输出的电压极限

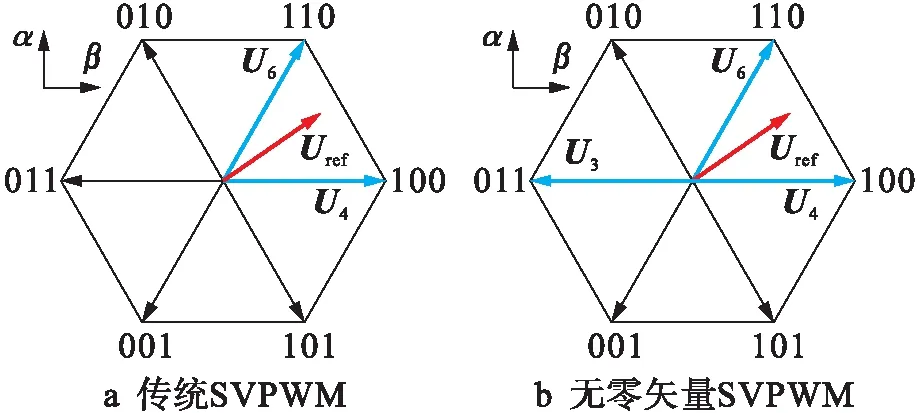
图5 两种空间矢量调制方法对比

本文采用调制方法的伏秒平衡方程为

(11)

选用的基本电压矢量幅值相等，方向相反，在合成零矢量时，把需要的零矢量作用时间T0平均分配给相对的基本电压矢量，由此可以求得各基本电压矢量作用时间，即

(12)

然后采用五段式调制方法，基本电压矢量的作用顺序为U4→U6→U3→U6→U4，这样可以实现PWM波形的对称，减少谐波.

3 仿真研究

为了验证所提方法的正确性和有效性，在Simulink环境下建立了双Y移30°六相永磁同步电机系统的仿真模型.仿真模型中，逆变器直流母线电压为400 V，PWM开关周期为0.000 1 s，电机模型参数为：极对数为3，转动惯量为0.015 kg·m2，定子电阻为1.4 Ω，定子直轴电感为8.8 mH，定子交轴电感为8.8 mH，定子漏感为2.9 mH，转子磁链为0.68 Wb，负载转矩初始值为20 N·m.在0.2 s时，负载转矩变为50 N·m，在0.4 s时，负载转矩变为30 N·m，电机转速的参考值为500 r/min.

图6为两种调制方法产生的共模电压仿真结果.图6a为四矢量SVPWM调制方法ABC相绕组结点共模电压的变化情况，在0.000 5 s内变化了40次且峰值为±200 V；图6b为新型抑制共模电压SVPWM调制方法ABC相绕组结点共模电压的变化情况，在0.000 5 s内变化了8次且峰值为±66 V.可以看出，相较于四矢量SVPWM调制方法，抑制共模电压SVPWM调制方法所产生的共模电压峰值降低了2/3，而变化频率也显著降低.

图6 两种调制方法下的共模电压变化情况

图7为两种调制方法产生的定子相电流仿真图.图7a为四矢量SVPWM调制方法A相电流波形；图7b为抑制共模电压SVPWM调制方法A相电流波形.相较于四矢量SVPWM调制方法，抑制共模电压SVPWM调制方法产生的电流谐波含量较高，经FFT分析此结论得到验证.负载转矩为50 N·m时，四矢量SVPWM调制方法的相电流谐波含量为THD=3.40%，如图8a所示；抑制共模电压SVPWM调制方法的相电流谐波含量为THD=6.17%，如图8b所示.

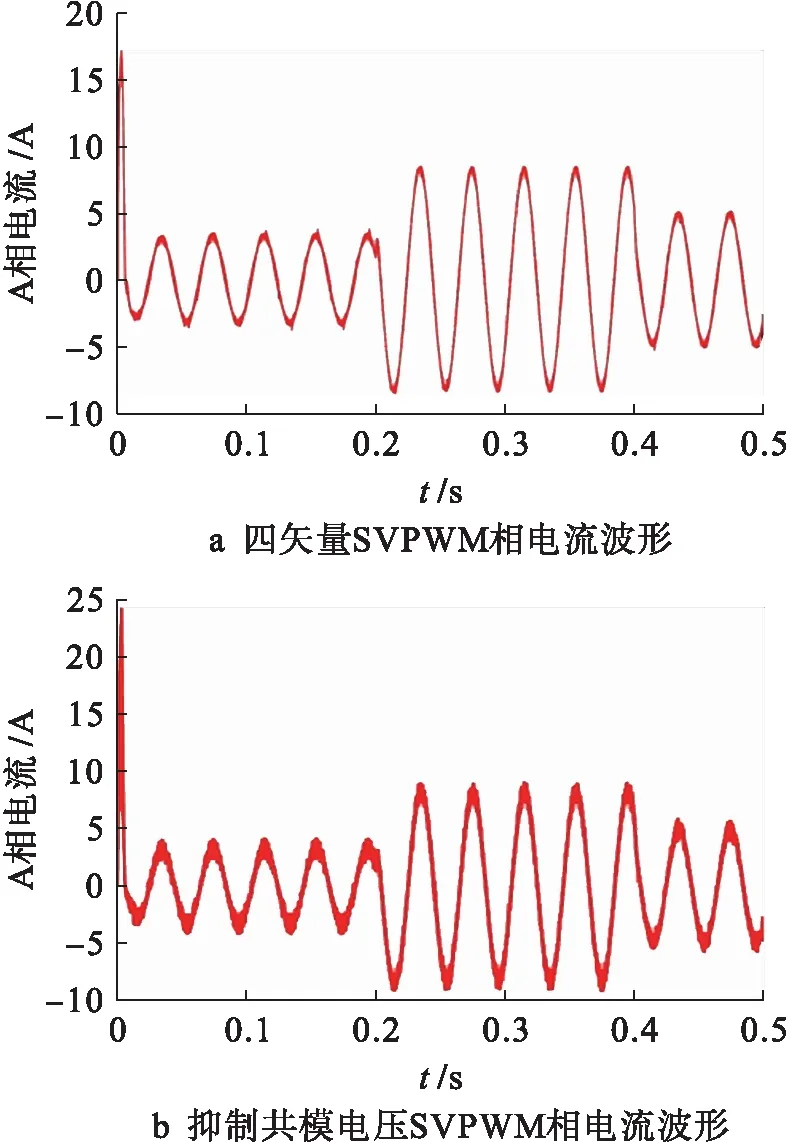
图7 两种调制方法下相电流波形

图8 两种调制方法下相电流FFT分析结果

图9为两种调制方法电磁转矩的仿真曲线.可以看出，相较于四矢量SVPWM调制方法，抑制共模电压SVPWM调制方法下的电磁转矩波动稍大，印证了FFT分析中抑制共模电压SVPWM调制方法电流谐波含量高的结论.

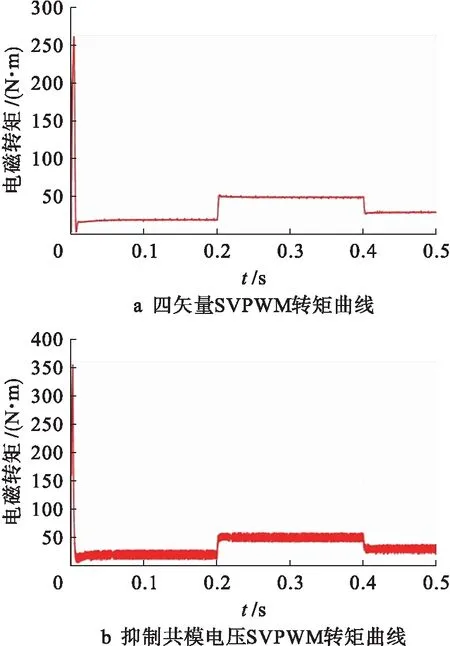
图9 两种调制方法下转矩曲线

4 结 论

本文以双Y移30°六相电机与两电平六桥臂电压源型逆变器组成的系统为对象，分析该系统共模电压的起因及特点.通过三相解耦的方式将电压矢量分解到两个三相逆变器中，并通过无零矢量合成的方式得到一种新的空间矢量调制方法，然后利用Simulink环境对该方法进行了仿真.仿真结果表明，该方法可以明显降低双Y移30°六相电机共模电压的幅值和频率，并且转矩性能、相电流正弦度与传统四矢量空间矢量调制方法近似，达到了设计目的.