基于ANFIS的超短期风电出力预测模型及仿真*
2020-06-10沙宇恒于海波
高 骞,程 霄,沙宇恒,于海波
(1.国网江苏省电力有限公司 发展策划部,南京 210024;2.北京国电通网络技术有限公司 规划与计划业务管理事业部,北京 100192;3.国家电网公司 发展策划部,北京 100031)
风电作为可再生清洁能源,能够替代化石能源并网消纳,有利于减少能源消耗,促进电力可持续发展.然而,由于风电出力的随机性和波动性会为大规模并网安全稳定运行带来很大风险,因此,需要提高风电的预测精度,以保障电网安全运行.目前,采用单一的风电出力预测方法很难满足风电预测的精度要求,即使在风电预测短周期(5~10 min)内,仍会有10%~20%的风电预测误差[1].同时考虑到风电场的差异化特点,若仅采用单一的预测方法很难满足风电实际运行要求.文献[2]通过建立人工神经网络模型对风电场24 h内的输出功率进行预测,该方法训练的结果基本吻合风电场实际功率曲线,但仍然存在很大的误差.文献[3]建立了风速预测模型,并结合基波神经网络拟合实际功率曲线,根据拟合曲线计算功率预测值.虽然该方法能提高运算效率,但在拟合实际功率过程中出现的误差会累积到预测功率的模拟当中,使得优化出的预测功率依然存在较大误差.文献[4]利用差分算法处理原始风速数据,并建立ARMA预测模型,取得了较好预测效果,但该模型的参数未能选取最优值,使得模型仍然不够准确.文献[5]利用小波变换的改进持续法对短期风电功率预测进行研究.该方法首先通过小波变换将信号高低分频,然后采用平滑法进行数据采样,最后利用持续法预测风电功率,该方法一定程度上过滤掉信号变异的部分,使得预测结果更加平滑,然而算例预测结果未能证明比其他的预测方法更为有效.虽然目前大部分学者开始利用组合预测方法开展风电短期预测工作,但绝大多数使用了各预测方法结果线性加权求和的方法,该方法求解各加权系数面临着很大困难,特别是当各方法的误差系数呈正相关性时,所得到的风电预测精度很难满足实际运行要求.
综上所述,本文提出了基于自适应神经模糊推理系统[6-7](ANFIS)的风电短期出力组合优化预测模型,并将各单一预测方法得到的预测结果作为ANFIS优化系统的输入信号,利用ANFIS优化功能模拟出风电输出功率.通过仿真算例结果可以看出,该模型方法优化出的风电预测精度要高于单一方法的预测精度.
1 风电预测模型
本文提出的风电预测模型并行运算组合优化的流程如图1所示.图1中风速-功率预测模型的编号用i来表示,其功率用Pi表示,各预测结果组合优化后的功率Pt表示为
Pt=F[P1,…,Pi,…,PI|θ]
(1)
式中:F为组合优化方案;θ为组合优化方案中所用参数.

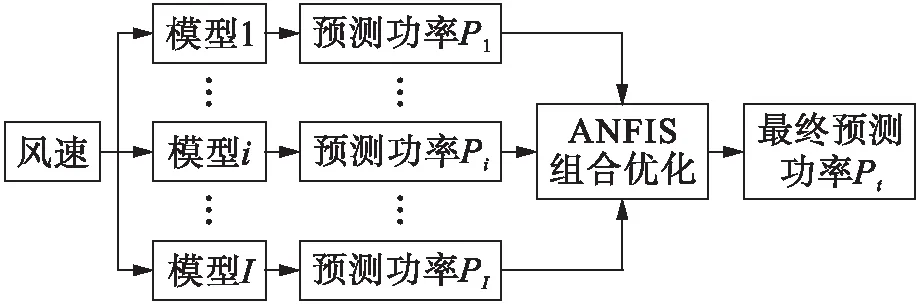
图1 风电模型组合模型图
2 ANFIS原理
自适应神经模糊推理系统凭借快速处理大规模数据和学习进化的功能,可以自动优化调整控制规则,建立适应各种规则的输出函数和隶属度函数.其中,比较典型的ANFIS原理框架图可分为五层,如图2所示.

图2 ANFIS原理框架图
第一层:将隶属度函数对应的输入量模糊化处理.X、Y对应节点的模糊集所采用的隶属函数为
(2)
式中,ai、ci分别为ANFIS系统中的条件参数.
第二层:规则层.不同节点分别代表对应的学习规则,并由各节点相互配合,共同完成系统的算子计算.其中,各节点的输出信号使用该节点各输入信号的积作为对应的信号强度.
第三层:标准层.将第二层对应节点的输出信号作为输入信号,该层节点的规则是该节点单个输入信号的强度与所有输入信号强度和的比值,依次可对相应节点完成模糊推理系统的可信度归一化工作,归一化表达式为
(3)

第四层:该层节点数与第三层相同,目的是保证第三层各对应节点的信号输出与第四层各对应节点的输入信号(即ANFIS信号录入)匹配链接,从而确保每个样本数据均能有效参与模糊推理的自适应进化学习.第四层对应各节点的输出信号代表了各规则对ANFIS结果的贡献度,即
(4)
式中,pi、qi、ri为ANFIS系统的效应参数.
第五层:输出层.将第四层对应的节点输出信号采用权重平均法求和,最终计算出ANFIS的结果,本文最终预测的风电场输出功率为
(5)
3 ANFIS的模糊C均值算法
3.1 模糊C均值算法
由于ANFIS中涉及的参数较多,因此采用一种高效寻优的方法是很有必要的.本文所采用的模糊C均值算法[8-10]作为一种高效的寻优算法,将各样本到聚类中心点的内距离最小加权平方和作为寻优ANFIS参数的优化目标,利用隶属度矩阵函数模糊划分各样本属于各聚类中心的程度,归一化后隶属度函数矩阵U的元素表示为
(6)
式中:E为聚类个数;uik为样本k隶属第i个聚类中心的函数.
算法选取的优化目标函数为
(7)
式中:V为聚类中心矩阵;m为加权指数;δik为样本k到第i类中心的距离.
结合拉格朗日法则[11-12]计算样本k隶属第i个聚类中心点的隶属度函数为
(8)
(9)
式中:dik为第i个聚类中心与第k个数据点间的欧几里得距离;xk为ANFIS第k个输入信号.
3.2 评价指标
采用国家能源局对风电功率预测管理规定的办法,建立以15 min为预测周期的评价指标.各指标含义如下:
日平均预测功率准确率表示为
(10)
(11)
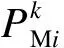
日平均预测功率合格率表示为
(12)
(13)
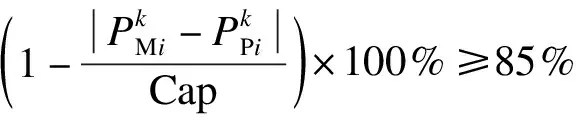
全天风电功率预测均方根误差为
(14)
本文所提方法的算法流程图如图3所示.
4 算例分析
本文采用某风电场的实测数据进行实验,该风电场的总装机容量为300 MW,总风机台数为150台,每台风机的额定容量为2 MW,采样时间为2017年6月1日至6月15日,数据采样间隔为15 min.1号风电机组和整座风电场的功率时序采样分别如图4、5所示.
以6月5日为例,通过优化仿真得到1号机组和整座风电场在不同预测方法下的评价指标,分别如表1、2所示.为了方便表述,将时间序列法(ARMA)、BP神经网络法、持续法和ANFIS法分别记为a法、b法、c法和d法.采用ANFIS法进行预测时,选取的训练次数为2 000次.
由表1、2可知,运用ANFIS方法进行风电功率预测时,无论单台机组或整座风电场,其准确率、合格率均高于其他三种方法的结果,且均方根误差低于其他三种方法.综上所述,利用ANFIS组合优化方法进行风电功率预测是有效的.
算法将风电机组汇聚成风电场群时,单台风电机组之间的输出功率可能出现互补和消性的情况,使得整座风电场的功率特性曲线要比单机组的功率曲线平缓,抑制了风电机组的突变功率.使用该算法后,风电场功率曲线的规律性提高,且预测精度也相应提高,这与表1、2的优化结果是一致的.

图3 ANFIS的模糊C均值算法流程图
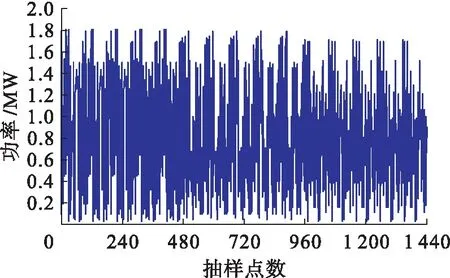
图4 1号风电机组功率时序采样
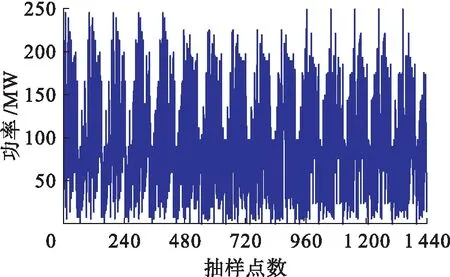
图5 整座风电场总功率时序采样
取1号单机组在6月5日上午8点到12点时间段内的单次测量结果,将4种预测方法下的预测值和真实值进行对比,结果如图6所示,各方法的预测误差对比如图7所示.
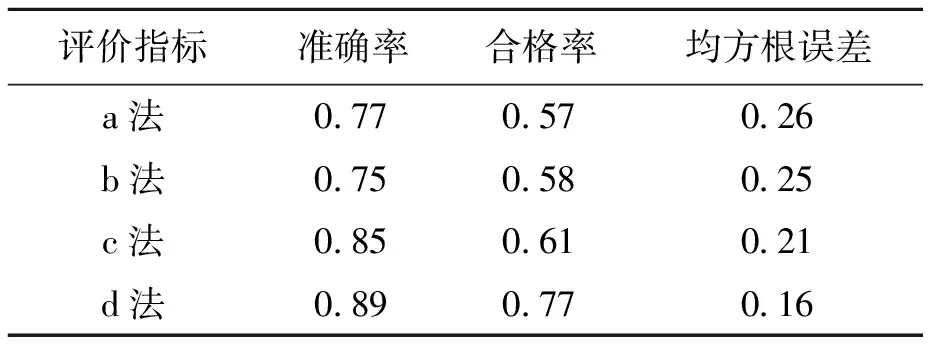
表1 1号风电机组4种预测方法的评价指标
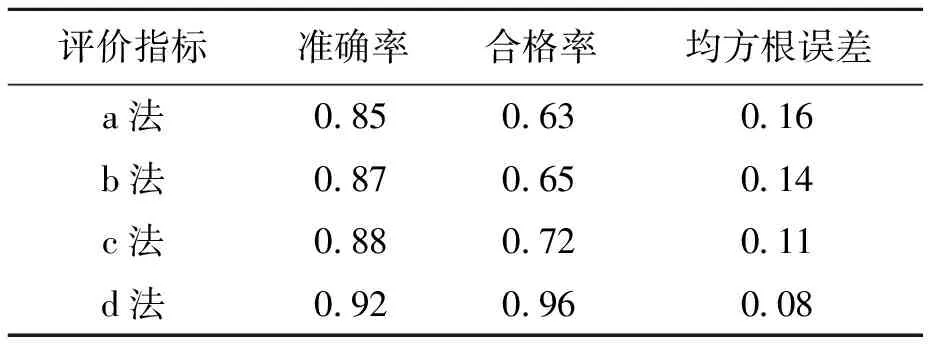
表2 整个风电场4种预测方法的评价指标
根据图6可知,文中ANFIS组合优化预测方法所得的预测结果更加趋近真实值,且从图7也可看出ANFIS方法的误差比其他三种预测方法预测误差更小.原因在于ANFIS组合优化预测风电功率的方法是将各预测方法的结果作为ANFIS系统信号输入,使得各输入信号平滑调和,并且通过ANFIS系统各层的优化模拟后,系统输出信号与真实值的误差减小,弥补了输出信号的失真,提高了预测精度.

图6 4种方法预测结果对比
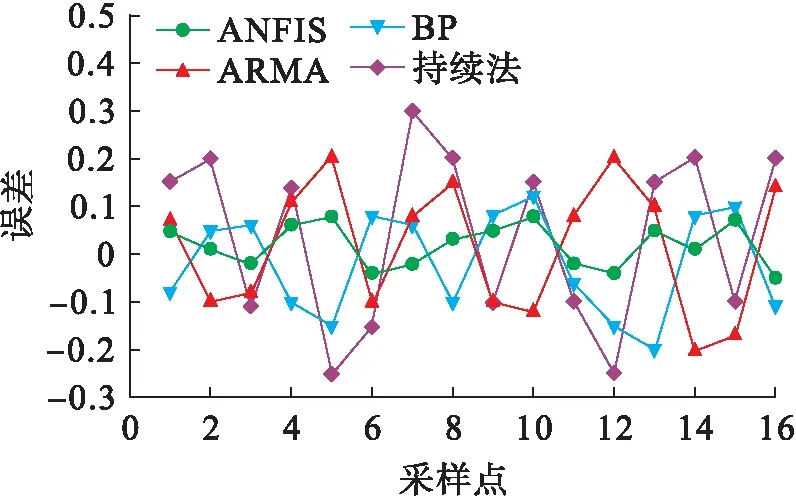
图7 4种方法预测结果误差趋势
5 结 论
单一预测方法在风电机组功率预测精度上存在较大误差,本文提出了一种ANFIS组合优化方法.将各预测方法所得的预测结果作为输入信号,经ANFIS组合优化系统再次模拟出最终风电输出功率.结合算例结果可以看出,ANFIS组合优化预测模型在进行风电短期机组出力预测时,能取得很好的预测精度.同时,对于整座风电场的预测精度要比单机组的预测结果要好,这与汇聚效应原理相符.
