基于组合赋权—TOPSIS 方法在砌体结构加固 方案中的应用
2020-06-09李义广冯晓爽李慧慧何洪明
王 永,李义广,冯晓爽,李慧慧,何洪明
(1.河北农业大学 城乡建设学院,河北 保定 071001;2.河北农业大学 理工学院,河北 保定 071001)
砌体结构的损害是经常出现的一大问题,显然应该着重研究砌体结构的修复,使其变得更加紧固。对于实际砌体结构加固工程项目而言,需要在众多加固方案中选择1 个综合效益最优方案对结构进行抗震加固,以达到预期的结果。
在常见的G1 法、熵值法、组合赋权法等的选优方案中,它们各自存在优势和劣势,如G1 法的客观性较弱,其合理性较差;熵值法具有局限性,其结果太过理想化;而组合赋权法具有全面性,克服其他方法的缺陷,其结果较为严谨,具有可信度。沈丹杰等[1]将灰色关联度理论基础上的TOPSIS 应用在桥梁的耐久性的评价中,使结果的科学性得以提升。王祎炜等[2]为选出装配式建筑施工安全方案,提出了基于灰色关联度TOPSIS法的方案优选方法,确定权重并进行选优。刘健等[3]为确定地热能开发区的最优方案,将灰色关联TOPSIS 法引入到热能开发区的优选中,并将结果应用到实际工程中。本文将组合赋权—TOPSIS 分析法引进到砌体结构的加固方案的优选中,建立了1 套数学理论,进一步完善砌体结构加固的优选方法,可为制定相应的加固方案提供参考。
1 评价指标体系
1.1 确立评价指标
本文的准则层相关指标是从经济费用、效果可靠、加固技术、社会效应4 个基本目标确定的,并在此基础上确立了砌体加固方案优选的子准则层评价指标体系。砌体结构加固方案的指标体系见表1。
1.2 指标值归一化处理
在上表的准则层和子准则层中,由于存在量纲的差异,故需对指标的量纲进行归一化处理。具体如下:
(1)对成本型指标处理的公式如下:

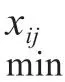
(2)对效益型指标处理的公式如下:

式中参数意义同上。
(3)定性指标的确定需要用等级集来表示,查阅相关文献[4]可以得知等级集为E={很差,差,较差,中,较好,好,很好},根据等级集对E 进行赋值,即E={0.05,0.20,0.35,0.50,0.65,0.80,0.95}。

表1 砌体结构加固方案评价指标体系Table 1 Evaluation index system of masonry structure reinforcement scheme
2 评价指标权重赋值
指标权重在整个方案中很重要,权重的认定方法有2 种,其一是主观法,而另外1 种则是客观法。客观法主要运用数学理论进行计算,而主观法则以人的主观意向为主导。本文以具有主观性的G1 法和具有理论性的熵值法为基础,然后将G1 法计算得到的值与熵值法计算得到的值通过组合公式得出1 个权重值,这样就能减弱各自劣势所带来的影响。
2.1 基于G1 法的指标权重赋值
G1 法是在AHP 法的不足的基础上而改进的1种确定权重的方法。与AHP 法相比,该方法不用再做判断矩阵的创建以及一致性检验等过程,从而使得计算不再过于复杂。
(1)对指标的影响性大小做排序

(2)专家依次对毗邻的2 个指标z*l 和z*
l-1 的影响性做比较,并依据专家的各自意向对相近2 个指标之比给定一特定的值,记为θi
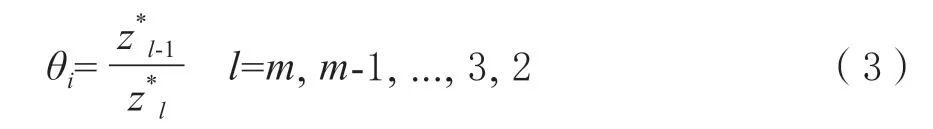
(3)采用G1 法确定对应的权重值

通过以上给定的θi求出影响性最小的指标权重ω*n(4)基于计算求出的ω*n 以及θi进一步求出所有的权重值,将所求得的权重看成1 个向量,即为ω1

2.2 基于熵值法的指标权重赋值
熵是1 种度量,与系统的信息量有关。若已知的信息越多,则其不确定性就越小,故其熵值也越小,指标的权重值越大;反之亦然。
(1)计算各指标熵值
熵值的相关公式如下:
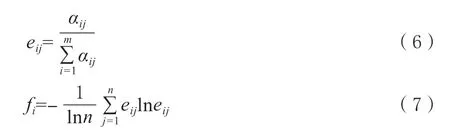
式中,fi为第指标i 通过计算而得出的熵值,eij为方案j 在指标i 下通过计算而得出的特征比重;αij为方案j 在指标i 所在项通过计算而得出的观测数据。
(2)计算各指标的权重

2.3 组合赋权
本文在砌体结构加固方案的优选应用中,先计算G1 法和熵值法的权重,再通过乘法合一的归一化组合权法确定综合权重,其公式如下:

3 方案优选方法分析的计算
TOPSIS 法是通过理想目标与各个方案的相对大小来比较,基于所得结果在所有方案中选择最优方案。通过比较各个方案与正理想解和负理想解的关系来确定方案的优劣程度,当某个方案与负理想解相差最大时,同时又与正理想解相差最小,证明该方案相对较好。灰色关联度分析是基于灰色关联理论的1 种用现有信息来研究未知信息的重要方法,其基本理论是将最优的评价指标数列作为参考数列,用该参考数列与其他数列进行比较,根据几何曲线的相似度来判断两者之间的联系紧密程度。将2 种方法进行组合综合考虑更具合理性,故在灰色关联度理论基础上改进TOPSIS 法更适用于本文。具体计算过程如下:
(1)构造加权规范化决策矩阵
把标准化决策矩阵Q0=(yij)m×n以及将G1 法计算得到的值与熵值法计算得到的值通过组合公式得出的权重向量ωi作乘法运算,使其运算结果组合成加权标准化决策矩阵:

(2)确定正理想解Q+和负理想解Q-
确定矩阵中各列的最大值和最小值,由各列中最大值组成的1 组数为正理想解,由各列中最小值组成的1 组数为负理想解。
(3)计算各方案的欧式距离Di+和Di-
(4)确定各方案到正、负理想解的灰色关联度

(5)确定各方案的灰色关联度系数Hi±

(6)对欧式距离和灰色关联度所得到的结果分别做统一标准的计算
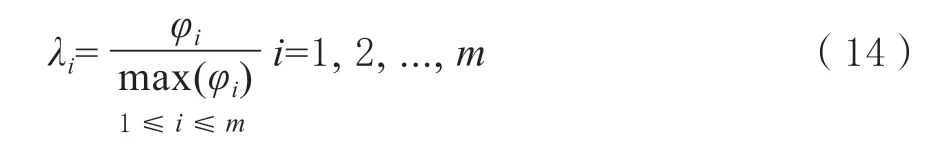
式中,Di±、Hi±统一表示为φi,归一化的计算数据通过di±、hi±表示。
(7)对做统一标准计算的欧式距离和灰色关联度乘以各自的分项系数进行求和计算
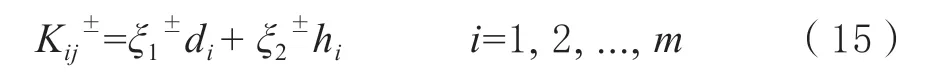
式中,ξ1和ξ2所表达的意思是最终方案确定者对方案的看重程度,ξ1和ξ2的具体数值大小由最终方案确定者员决定,但两者必须满足ξ1+ ξ2=1。

(8)计算各方案的相对贴近度ki通过相对贴近度ki的大小来进行比较选优,ki的值越大的方案其方案也就越合理。
4 工程应用
现以河北农业大学水利楼为例,以3 种加固方案为基础,即钢筋网水泥砂浆面层加固、钢筋混凝土面层加固、钢绞线—聚合物砂浆面层加固[5],然后将所阐述的方法应用到水利楼的加固方案中。
4.1 加固方案确定
本文选用3 种常见的砌体加固方案,分别为上述所介绍的3 种加固方案,这3 种方案的具体的材料等级、尺寸大小等参数如下表2。

表2 各加固方案参数Table 2 Parameters of each reinforcement scheme
4.2 评价指标值的规范化
经调研实例可知计算得到了各加固方案的评价指标值,对于定性指标,应用因素等级集,即E={很差,差,较差,中,较好,好,很好},并赋值为E={0.05,0.20,0.35,0.50,0.65,0.80,0.95}。综合多名专家的意见并经过全面地考虑,得到1 套评价指标值,将各指标按照规范化公式进行处理,从而得到砌体加固方案的决策矩阵Q0。

4.3 权重赋值
(1)确定准则层的权重
首先对准则层的各指标做影响性排序,则有X1>X3>X2>X4,准则层的影响性系数分别为θ1=1.1,θ3=1.4,θ2=1.6,故可得到准则层的权重向量ω1'
ω1'=(0.337 0.219 0.307 0.137)
(2)确定子准则层的权重
与准则层的权重计算过程相同,子准则层的 影 响 性 排 序 分 别 为X11>X13>X12,X21>X22>X23,X31>X32>X33,X42>X43>X41,故可得到子准则层的权重向量ω1''
ω1''=(0.404 0.259 0.337 0.412 0.343 0.245 0.439 0.338 0.225 0.258 0.434 0.310)
(3)将以上两步得到的数值作乘法运算得到G1法权重ω1
ω1=(0.136 0.087 0.114 0.090 0.075 0.054 0.135 0.104 0.069 0.035 0.059 0.042)
(4)通过熵值法得到指标权重值ω2
ω2=(0.253 0.297 0.253 0.002 0.007 0.007 0.030 0.021 0.044 0.013 0.042 0.031)
(5)运用组合公式计算得到的组合权重ωi
ωi=(0.332 0.249 0.278 0.002 0.005 0.004 0.039 0.021 0.029 0.004 0.023 0.013)
4.4 TOPSIS 法结果的相关计算
(1)通过计算得到加权规范化决策矩阵Q

(2)对加权标准化矩阵中数进行对比,并将各列向量中的最大值组成Q+和最小值组成Q
Q+=(0.332 0.249 0.278 0.002 0.005 0.004 0.031 0.020 0.028 0.003 0.012 0.010)
Q-=(0.000 0.000 0.000 0.002 0.003 0.003 0.014 0.011 0.010 0.002 0.005 0.005)
(3)确定各方案分别到正、负理想解的欧式距离D+和D
D+=(0.170 0.228 0.081)
D-=(0.198 0.147 0.203)
(4)计算各方案的灰色关联度系数H±i
Hi+=(0.904 0.872 0.926)
Hi-=(0.889 0.942 0.841)
(5)对基于以上算法得出的欧式距离和灰色关联度系数分别做统一标准计算
d+=(0.746 1.000 0.355)
d-=(0.975 0.724 1.000)
h+=(0.976 0.942 1.000)
h-=(0.944 1.000 0.893)
(6)将欧式距离和灰色关联度系数所得到的结果分别乘以各自的分项系数做求和,可得:
K+=(0.861 0.971 0.678)
K-=(0.960 0.862 0.947)
(7)计算各方案的相对贴近度
ki=(0.473 0.530 0.417)
4.5 计算结果的比较
基于以上理论可以得知方案优差与相对贴近度ki成正相关,即相对贴近度ki的值越大加固方案的整体效果就越好。根据计算得出的相对贴近度可以看出k2>k1>k3,即对于本文的3 种砌体结构加固方案而言,方案二的整体效果相对其他2 种方案最好。对于实际工程中的砌体加固来问题来说,应优先选择方案二。在3 种加固方案中,方案三的整体效果最差,故尽量不使用方案三的加固方案。本文所得出的结果与仅使用TOPSIS 法[6]或仅使用灰色关联度法所得出的结果相同,故验证了本文所采用的方法可以应用在砌体结构加固方案优选中。
5 结论
砌体结构加固优选是1 个从多个复杂方案中确定出最优方案的过程,具有随机性、合理性。本文所选出的最合理的方案是运用了G1法和熵值法得到的权重进行计算组合,克服了一定的缺陷,其可信度很高[7]。组合赋权在一定程度上增强了客观性,使得最终结果让相关人员更容易接受。与TOPSIS法或灰色关联度法相比,本文所采用的基于灰色关联度理论的TOPSIS 法得出的结果更具合理性和科学性,并且该方法不仅能对各个方案的整体情况作出准确判断,还可以看出各个方案中的相关因素的态势变化和最优方案这两者之间存在的差别,故在相关的优选问题中可首先考虑本文所采用的方法,同时该方法的步骤相对复杂,需要大量的数据支撑;本文通过河北农业大学水利楼工程实例详细地阐述了采用组合赋权—TOPSIS 法在砌体结构加固应用的计算过程,并验证了该方法可以应用在砌体结构加固中,但该理论既有优点又有缺点,要根据实际情况进行取舍。
