一种基于随机序列的正交离散频率编码信号*
2020-06-08贾基东李淑秋
贾基东 李淑秋 李 宇
(1 中国科学院声学研究所 北京 100190)
(2 中国科学院大学 北京 100049)
(3 中国科学院先进水下信息技术重点实验室 北京 100190)
0 引言
探潜技术与潜艇隐身技术是水下目标探测中的矛与盾,为了提高探测能力,声呐的发展经历了从单水听器到多元阵列、从窄带处理到宽带处理的过程。随着多基地声呐、水下传感器网络、多输入多输出(Multi input multi output,MIMO)声呐等新型声呐的出现,声呐技术开始向分布式、空间分集的方向发展[1-3]。匹配滤波技术是主动声呐接收端常采用的一种算法,为避免分布式系统中各发射信号在接收端彼此形成干扰,实现空间分集要求发射正交信号。
在通信中,设计正交信号的方法有时间分集、频率分集、波形分集。在水下探测中,时间分集意味着低探测效率,频率分集意为着低带宽利用率,因此波形分集是一个最好的选择。实现波形分集的一种常用方法是频率调制,离散频率编码信号因为其模糊函数的一些特性而引起了人们的广泛关注[4-6]。
离散频率编码信号彼此间的正交性好坏与频率编码序列密切相关。目前关于构造频率编码序列的方法研究主要分为两类:一类是基于有限域和本原元理论的方法[7-12],另一类是基于混沌序列的方法[13-17]。文献[7]中作者定义了一种汉明相关函数来描述序列间的正交性,并给出了基于有限域和本原元理论设计频率编码序列的汉明相关理论下界。本文在仿真分析部分也将采用汉明相关函数来比较本文算法与对比算法的优劣。文献[8]中作者基于代数结构设计了一种素数码长序列的生成方法,并推导了信号的模糊函数。在文献[12]中作者将基于有限域理论设计的编码序列长度推广为素数的倍数。尽管如此,基于有限域理论的编码序列长度只能是某些值仍是这类方法的一大缺点,严重限制了其在实际应用中的价值。相比之下,能生成任意长度序列的基于混沌序列的设计方法则更为实用。文献[14]中作者将Logistic 混沌序列映射为跳频序列,并分析了序列的汉明相关性。在文献[16]中,作者分析讨论了基于几种混沌序列设计的离散频率编码信号在模糊函数、正交性上的优劣,得出Bernoulli 混沌序列在离散频率编码信号设计中性能较好的结论。文献[17]中作者将线性调频信号应用到基于Lorenz 混沌的频率编码信号内部构造中,改善了信号的自相关性能。基于混沌序列能够设计任意长度、任意数量的编码序列集,但混沌序列表现出的随机性并不够强。
设计正交离散频率编码序列的关键是使码元的随机性足够好,因此本文将生成伪随机数的线性同余法应用于频率编码序列的构造,设计了一种基于随机序列的正交离散频率编码信号,并与文献[16—17]中的方法进行比较,得出了一些有用的结论。
1 离散频率编码信号
假设信号的一个编码序列为Q={q0,q1,···,qN-1},Q为序列Q0={1,2,···,N}的一个排列,Q0对应的信号频率序列为F0={f0,f1,···,fN-1},与Q相对应的信号频率序列为F={f0,f1,···,fN-1},则码元到频率的映射关系为
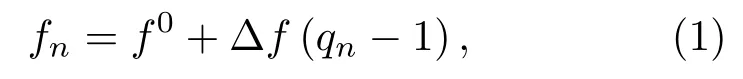
其中,f0为信号的载频,Δf=fi+1-fi为编码的步进频率,如图1所示。

图1 频率序列到编码序列的映射关系Fig.1 The relationship of the frequency sequence and the coding sequence
离散频率编码信号的数学模型可以描述为
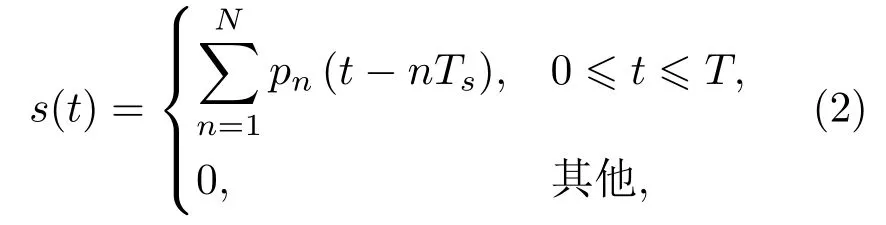
其中,T表示信号总时长,N表示编码序列长度,Ts=T/N表示子脉冲时长,pn(t)表示单个码元对应的子脉冲,表示为
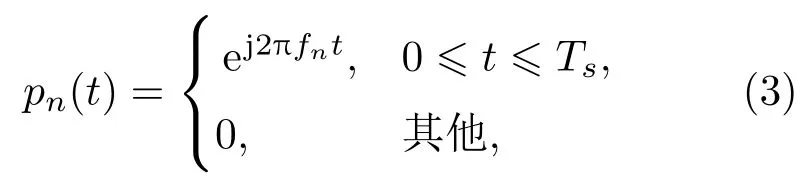
其中,fn表示与码元mn相对应的子脉冲频率。
2 正交频率编码集
2.1 Lorenz混沌序列
Lorenz 混沌是一种连续时间混沌系统,由美国著名的气象学家Lorenz 提出,可描述为如式(4)的方程组[17]:
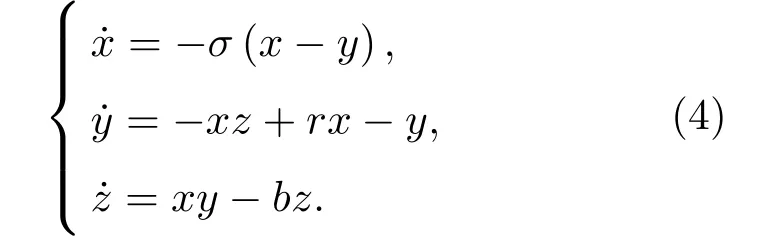
当式(4)中3 个参数σ、r、b满足如式(5)时,Lorenz系统会出现混沌解。
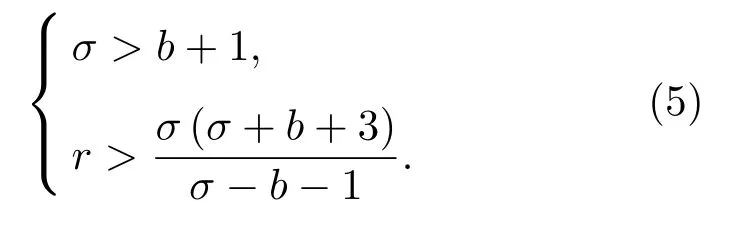
采用四阶龙格库塔法求解Lorenz方程组,设定采样率为2000 Hz,可得到3 个状态变量x(t)、y(t)、z(t)的采样序列。图2是一个Lorenz 系统的三维演示图,其状态轨迹反复折叠形成一个类似蝴蝶的图形,在3 个维度上均有界,吸引子上也没有交叉点,表现出整体混沌局部稳定的特点。图3是Lorenz系统3个状态变量的时间序列,3个序列均表现出非周期性和对初值的敏感性,当初值出现很小的变化时所得到的时间序列就出现很大的变化。变量x(t)的采样序列在信号处理特性上优于y(t)和z(t),因此在构造正交编码时通常采用x(t)的采样序列。
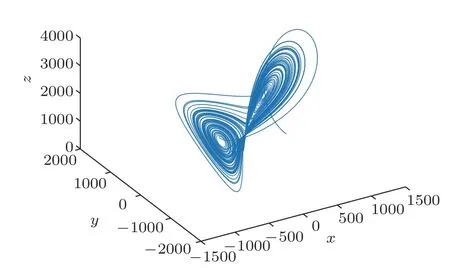
图2 Lorenz 混沌运动轨迹Fig.2 The movement of the Lorenz chaos
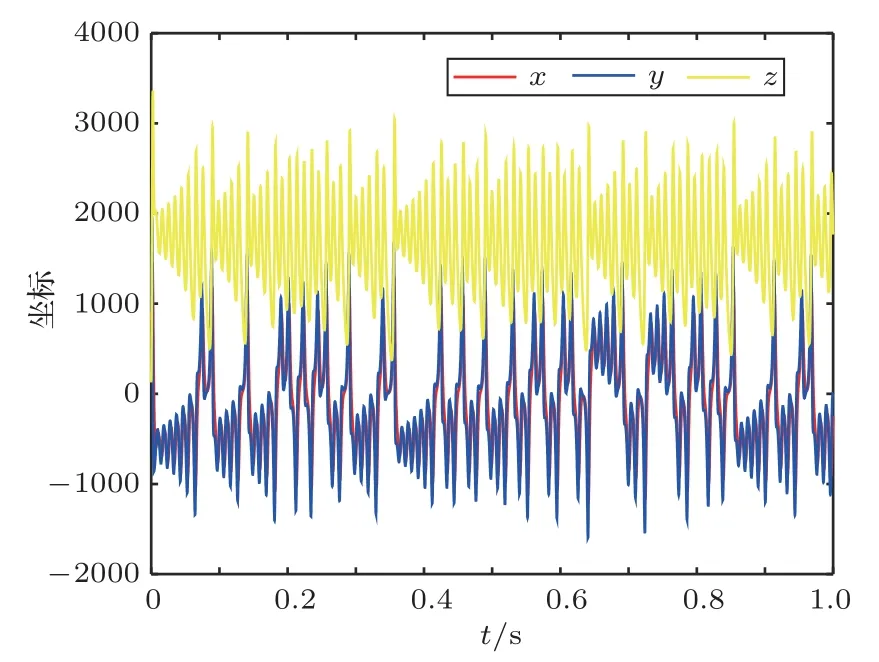
图3 Lorenz 混沌3 个状态变量的时间序列Fig.3 The time sequence of three states in the Lorenz chaos
2.2 Bernoulli混沌序列
Bernoulli 混沌是一种离散时间混沌系统,可描述为如式(6)的更新方程[16]:
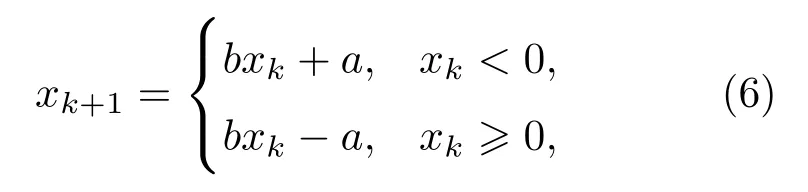
其中,a、b为混沌映射参数,a=0.5,b=2-ε,ε为一接近于0 的极小正值。xk∈[-0.5,0.5)为过程变量,b值越接近2,混沌序列值在混沌吸引域[-0.5,0.5)的遍历性越好,一组Bernoulli混沌序列如图4所示。
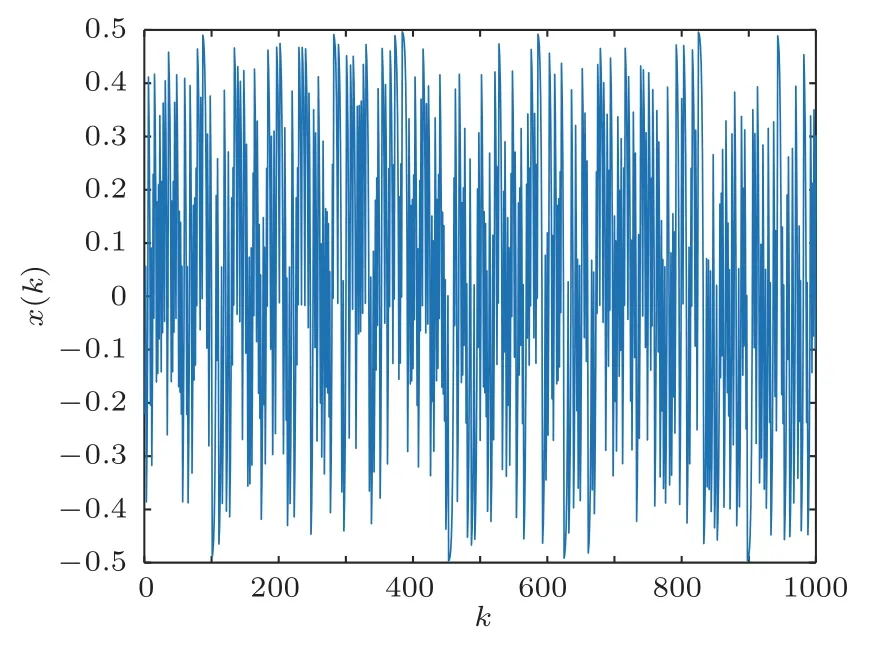
图4 Bernoulli 混沌序列Fig.4 The time sequence of the Bernoulli chaos
2.3 随机序列
线性同余法是一种简单常用的均匀随机数生成器,其递推式表述为


图5 线性同余随机序列Fig.5 The random sequence of the linear congruential generator
其中,参数a、b、C分别称为乘子、增量和模。关于参数的选取已有许多的研究,一个十分著名的随机数发生器是[18]

这种参数选取方法的主要考虑是便于计算机实现和受平方根准则的影响,该参数取值下的一组线性同余随机序列如图5所示。
2.4 正交频率编码集的构造
假设由混沌系统或随机过程产生的混沌序列或随机序列为{x0,x1,···,xi,···},从中截取M段长度为N点的序列,表示为
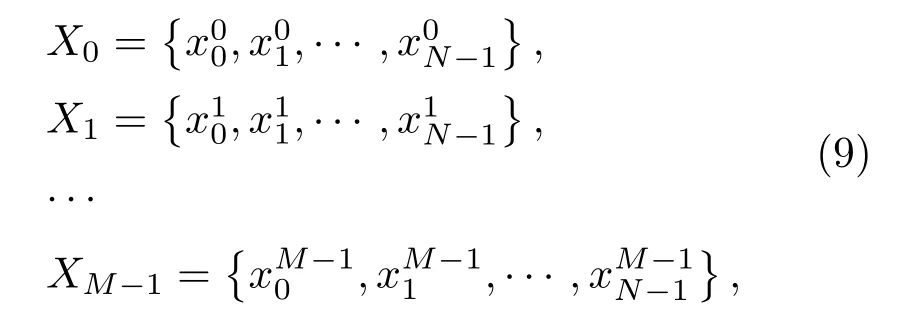
其中,M表示信号集中的信号总数,N表示单个信号的编码长度。
对于混沌信号,由于初值的影响和临近序列间的相关性较强,通常在截取时会采用抛弃混沌序列前面的一段和间隔截取两种手段来提高信号间的正交性。对于随机序列,由于各个时刻的随机变量在统计上都独立同分布,因此不存在这些问题。
对于第m段序列Xm,不妨按从小到大的顺序对其进行排列,得到排序后的新序列为
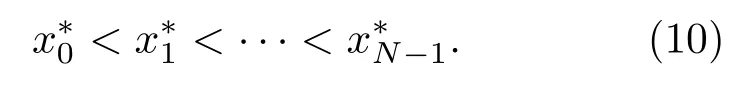
新序列中各元素在原序列中的位置索引构成的序列为

则序列Qm即为第m个信号的频率编码。
从截取后的混沌序列或随机序列到最终信号的频率序列间的映射关系可表示为
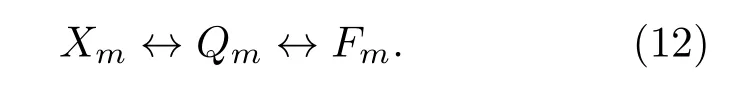
3 性能分析
信号的模糊函数描述了信号的时频域联合特性,模糊度图则反映了目标距离、速度的测量精度,下面分别对此进行分析。
3.1 模糊函数
信号s(t)的时延多普勒模糊函数定义为[8,19]
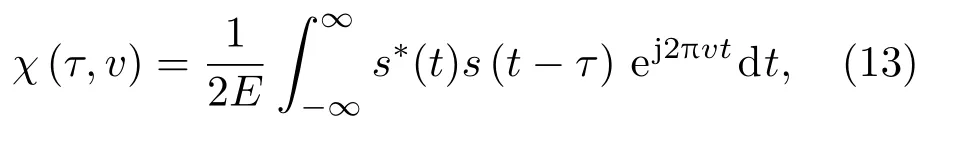
其中,τ表示时延,v表示多普勒频移,*表示共轭运算,E表示信号s(t)的总能量,如式(14)所示:
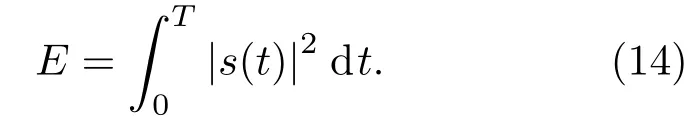
将式(2)、式(3)带入式(14),得到

将式(2)、式(15)代入式(13),得到

定义子脉冲的互模糊函数:
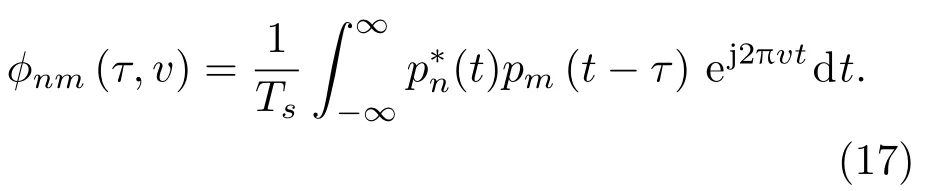
代入式(3),得到
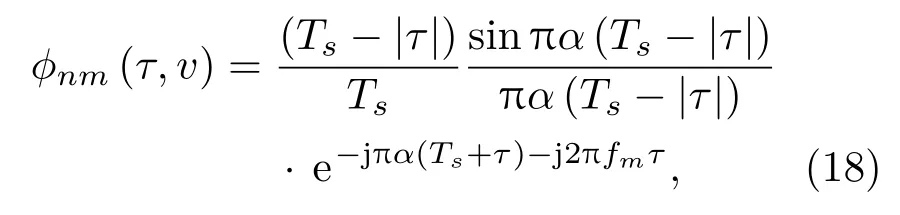
其中,α=fn-fm-v。
令m=n,则得到子脉冲的自模糊函数:
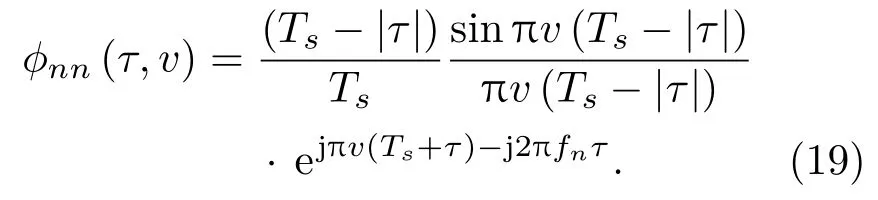
注意式(18)、式(19)均为|τ|≤Ts的情况,当|τ|>Ts时,

重新考虑式(16),则可以将其表述为
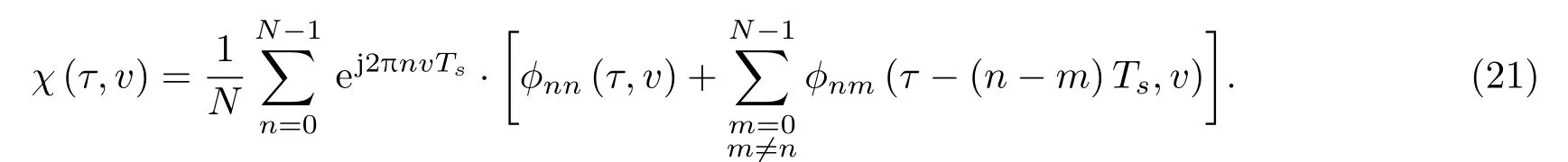
3.2 时延、频移测量精度
将信号的模糊函数下降到最大值0.707 倍(-3 dB)处的截面图定义为模糊椭圆或信号的模糊度图,反映了目标距离、速度的测量精度。
令τ= 0,有φnm(0,v)= 0,因此信号的模糊函数可以表示为

考虑到如式(23)的变换:

代入式(19),得到
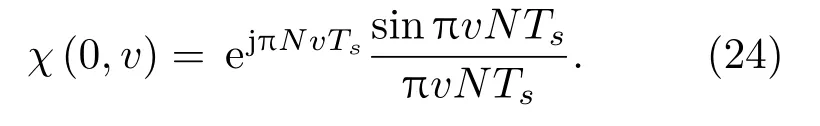
两边取模,有
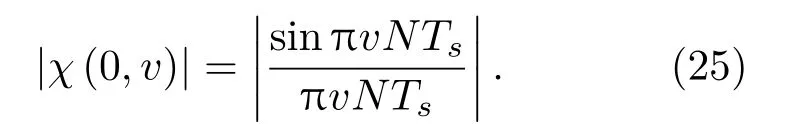
从式(25)可以看出,离散频率编码信号模糊函数在τ= 0 的平面表现为sinc 函数形式,信号的频移测量精度只与信号总时长T=NTs有关。|χ(0,v)|的第一个零点位置为±1/T,定义以模糊度图与频移轴两个交点间频移差的一半为频移测量精度,则信号的多普勒频移测量精度为

即信号的多普勒测量精度与信号时长成反比。
令v=0,由式(1)可得
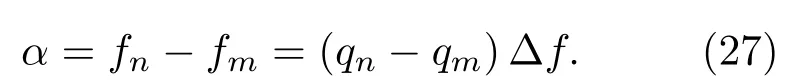
将式(27)代入到式(18),得到
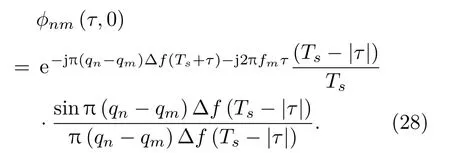
当τ →0时,其中sinc项
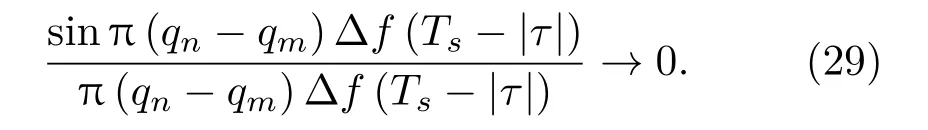
因此,当τ →0时
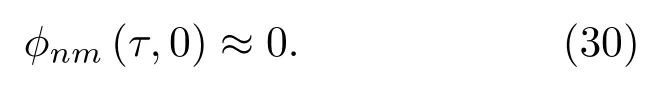
则信号的模糊函数可以近似表示为

代入式(19),得到

两边取模,有
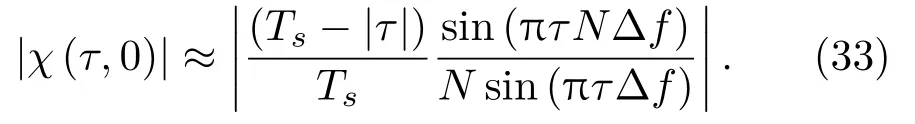
从式(33)可知,离散频率编码信号模糊函数的时延测量精度与信号的总带宽B=NΔf有关。|χ(τ,0)|第一个零点的位置为±Ts/N,定义以模糊度图与时延轴两个交点间时延差的一半为时延测量精度,则信号的时延测量精度为
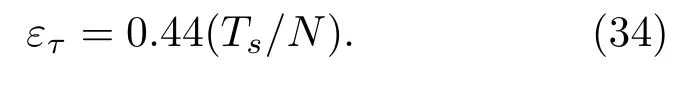
当TsΔf ≈1时,则
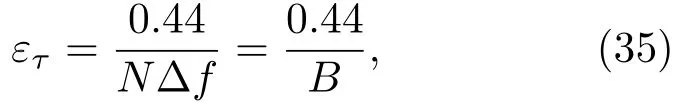
即信号的时延测量精度与信号带宽成反比。
由式(26)和式(35)可知,离散频率编码信号的频移测量精度和时延测量精度只与信号的时长和带宽有关,而与具体的编码序列无关。因此,对于正交离散频率编码信号集的设计,应该主要关注信号间的正交性设计,通过设计正交的频率编码序列,来提高信号间的正交性能。
3.3 正交性分析
假定由两个长度都为N的不同序列Qx,Qy编码得到的两个信号分别为sx(t)、sy(t),则两个信号的互模糊函数定义为
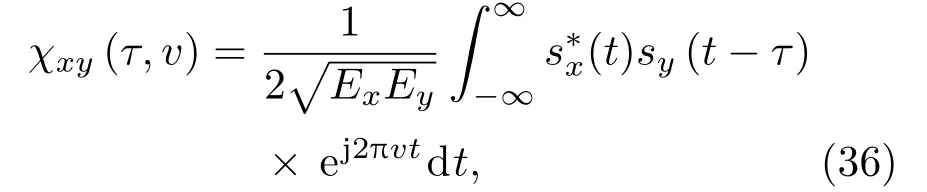
其中,Ex、Ey分别为信号sx(t)、sy(t)的能量大小。将式(2)、(3)代入式(36),得到

其中,
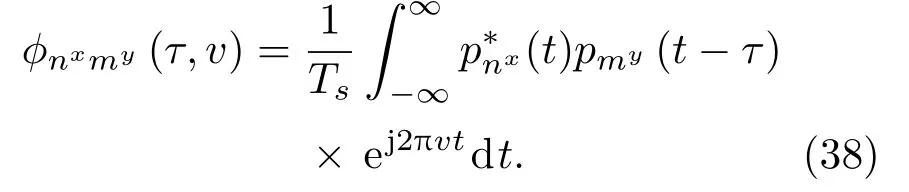
由3.1 节、3.2 节的分析可知,当nxmy时,φnxmy(τ,v)对χxy(τ,v)的贡献很小,χxy(τ,v)中的峰值都主要来自于nx=my时φnxmy(τ,v)贡献的能量,即当编码序列Qx,Qy中的相同码元在时域重叠时会使互模糊函数产生峰值,重叠的相同码元越多,峰值越高。因此,对于自模糊函数来说,只要编码序列是满码序列(每个码元都在序列中出现且仅出现一次),自模糊函数就能表现为近似理想的“图钉型”函数。对于互模糊函数来说,则要设计尽可能不会出现码元重叠的序列,来使不同离散频率编码信号间有足够好的正交性。
对于随机序列,由于在任意不同时刻都互不相关,因此在任一时延下两个不同序列相同码元重叠的概率都很小,即
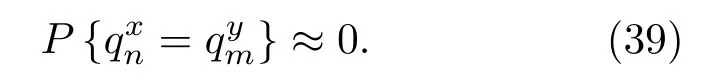
因此,信号sx(t)、sy(t)的互模糊函数
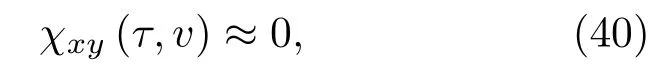
即信号sx(t)、sy(t)彼此间正交。
4 仿真分析与讨论
按照上述第3节所描述的离散频率编码序列的生成方法,分别基于Lorenz 混沌序列、Bernoulli 混沌序列和随机序列设计离散频率编码序列。码长25、编码数为2 时3 种方法各自生成的编码序列如表1所示。设定采样率为10 kHz,信号时长为1 s,带宽为1 kHz,信号载频为500 Hz,相应离散频率编码信号的自模糊函数和互模糊函数如图6所示。从中可以看出,3 种方法设计的离散频率编码信号均具有“图钉状”的理想自模糊函数,且互模糊函数峰值都较小,而基于随机序列编码的信号相比另外两种方法设计的信号互模糊函数峰值更小。
截取图6中3 种设计方法得到信号的自模糊函数的v= 0 平面和τ= 0 平面,分别得到3 种设计方法的时延相关函数和多普勒相关函数,如图7所示。从中可以看出,3 种信号时延相关函数和多普勒相关函数的主瓣基本重合,即3 种方法设计的信号具有相同的时延测量精度和多普勒测量精度,这是因为尽管3 种设计方法得到的信号编码序列不同,但所采用的信号时长和信号带宽均相同。这与3.2 节对于离散频率编码信号的时延测量精度和多普勒测量精度的理论分析结果一致,即信号的时延测量精度与信号带宽成反比,信号的多普勒测量精度与信号时长成反比。3 种设计方法采用了相同的信号时长和信号带宽,因此具有相同的时延测量精度和多普勒测量精度,表现在时延相关函数上和多普勒相关函数上即各自的主瓣基本重合。

表1 3 种方法生成的编码序列Table1 Coding sequences of three methods
为了比较本文方法和文献[16—17]方法设计的离散频率编码信号在信号集正交性上的性能,首先定义如下的序列集归一化最大汉明相关函数:
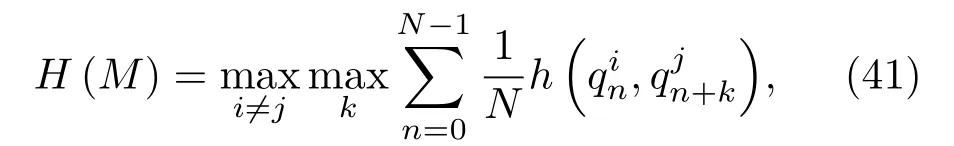
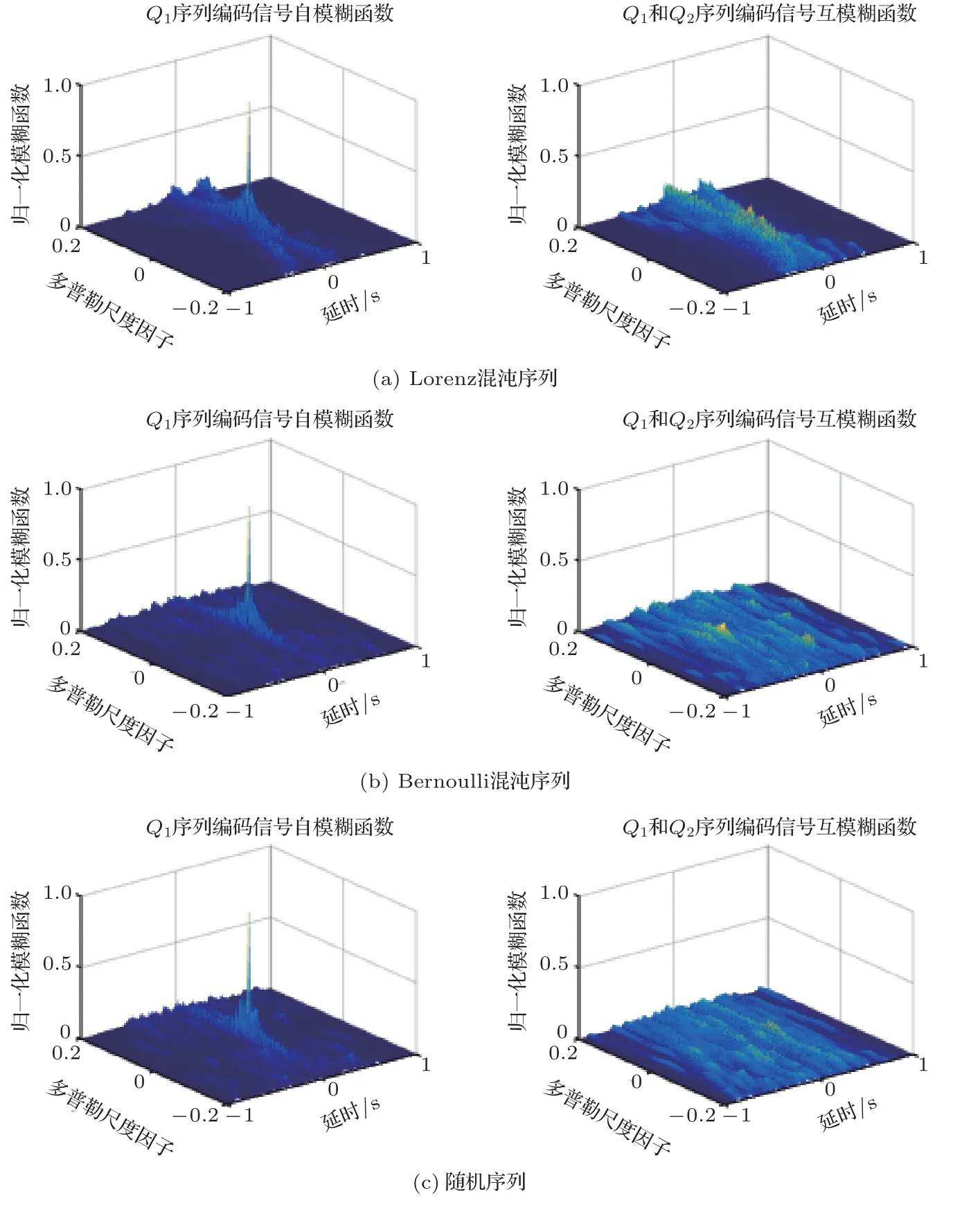
图6 3 种方法设计信号的模糊函数Fig.6 Ambiguity functions of signals designed by three methods
其中,qin为频率编码序列Qi的第n个码元,为频率编码序列Qj的第n+k个码元,N表示编码序列长度,M表示序列集中的序列个数,0 ≤i,j≤M -1。函数表示为

类似的,定义如下的信号集归一化最大时延相关函数:

其中,函数Rij(τ)为信号si(t)和信号sj(t)的归一化时延互相关函数,si(t)表示序列Qi编码的信号,sj(t)表示序列Qj编码的信号,M表示信号集中的信号个数,0 ≤i,j≤M -1。
设定编码序列长度为50,信号采样率为10 kHz,信号时长为1 s,带宽为1 kHz,信号载频为500 Hz,生成的序列个数或信号个数M从2 变化到50,进行100 次蒙特卡洛仿真取平均,式(40)、式(42)定义的序列集归一化最大汉明相关函数和信号集归一化最大相关函数的变化曲线如图8所示。对比3种方法的变化曲线可以看出,基于随机序列生成的序列集和信号集的最大相关函数值更小,基于Bernoulli 混沌的方法次之,基于Lorenz 混沌序列的方法生成的信号彼此间相关性较强。另外,最大的相关函数值随着信号集中信号数量的增加而逐渐变大,这与理论定性分析的结果一致。对比序列集归一化最大汉明相关函数和信号集归一化最大相关函数的变化曲线图还可以看出,两种曲线的变化规律一致,即序列集的正交性决定了信号集的正交性,这与3.3 节的正交性分析结果也是一致的。

图7 3 种方法设计信号的时延相关函数和多普勒相关函数对比图Fig.7 The comparison of three methods on delay correlation and Doppler correlation of signals
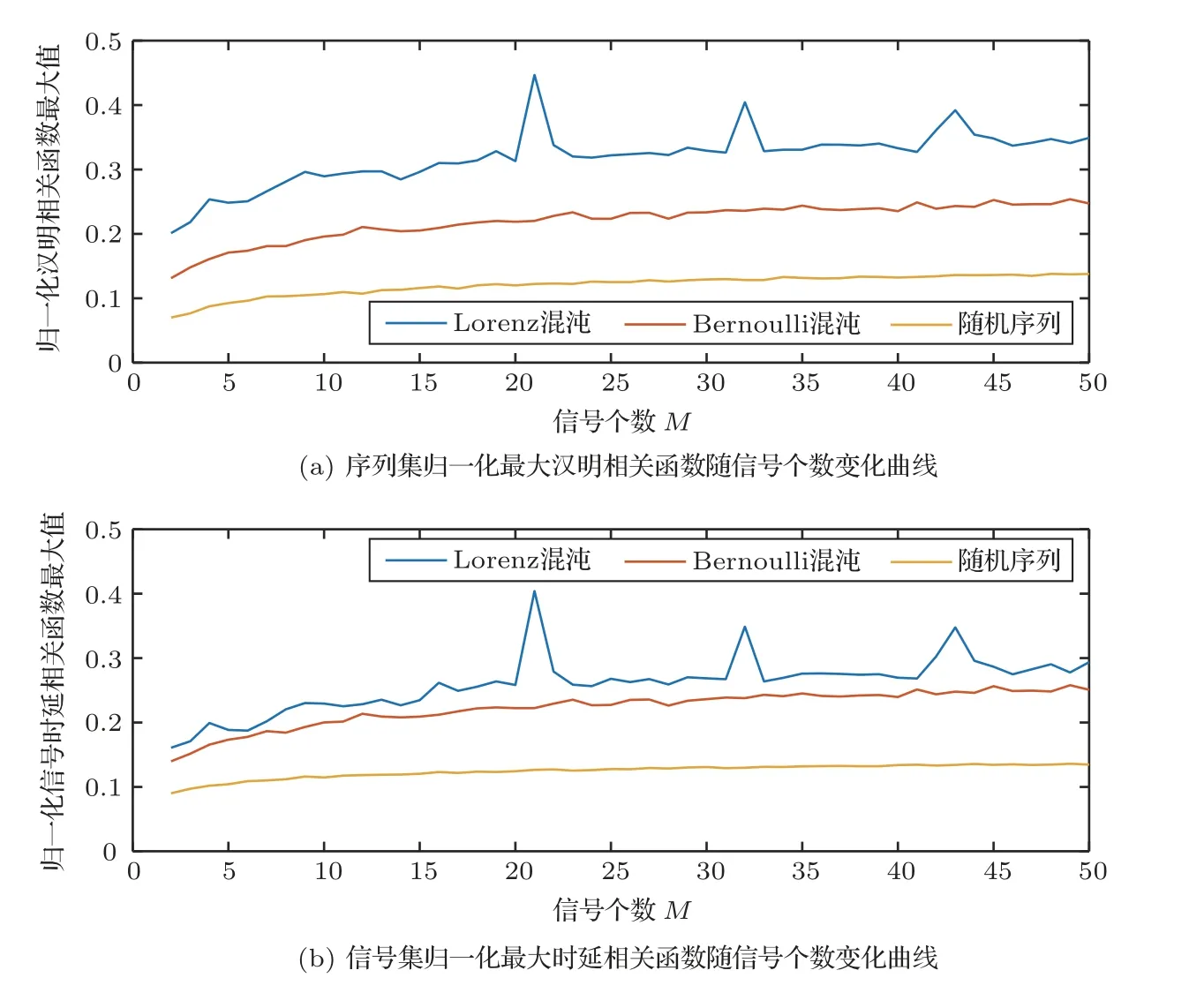
图8 序列汉明相关函数最大值与信号时延相关函数最大值随信号个数变化Fig.8 The changing of the maximum of Hamming correlation and the maximum of delay correlation
5 结论
与混沌序列相比,线性同余随机序列具有更强的随机性。本文基于线性同余随机序列设计离散频率编码信号,并与文献[16—17]提出的基于Lorenz混沌序列和基于Bernoulli 混沌序列设计离散频率编码信号的方法进行了比较。从理论上推导了离散频率编码信号的模糊函数,并分析得出离散频率编码信号的时延测量精度取决于信号带宽,多普勒测量精度取决于信号时长。对基于随机序列编码的离散频率编码信号的正交性从理论上进行了定性分析,得出不同信号彼此间的正交性主要取决于信号编码序列的码元重叠数量,基于随机序列编码的离散频率编码信号能取得较好的正交性,并通过仿真实验对这一结论进行了对比验证。
