建立数学模型解决“巡检线路排班”问题
2020-06-08吕宁宁潘娜娜
吕宁宁,潘娜娜,董 慧
(1.安徽工业经济职业技术学院,安徽 合肥 230051;2.安徽新华学院,安徽 合肥 230088)
1 问题描述
1.1 背景资料
某化工厂有26个点需要进行巡检以保证正常生产,各个点的巡检周期、巡检耗时、两点之间的连通关系及行走所需时间已知。
每个点每次巡检需要1名工人,巡检工人的巡检起始地点在巡检调度中心,工人可以按固定时间上班,也可以错时上班,在调度中心得到巡检任务后开始巡检。现需要建立模型来安排巡检人数和巡检路线,使得所有点都能按要求完成巡检,并且耗费的人力资源尽可能少,同时还应考虑每名工人在一定时间段内(如1周或1个月等)的工作量尽量平衡。
1.2 问题提出
问题1,如果采用固定上班时间,不考虑巡检人员的休息时间,采用每天3班倒,每班工作8 h左右,每班需要多少人,巡检线路如何安排,并给出巡检人员的巡检线路和巡检时间表。
问题2,如果巡检人员每巡检2 h左右需要休息1次,休息时间大约是5~10 min,在12时和18时需要进餐1次,每次进餐时间为30 min,仍采用每天3班倒,每班需要多少人,巡检线路如何安排,并给出巡检人员的巡检线路和巡检时间表。
问题3,如果采用错时上班,重新讨论问题1和问题2,试分析错时上班是否更节省人力。
2 问题分析
不论固定上班还是错时上班,工作人员都是从调度中心开始进行工作,但是离该点较远的地方就要直接派工人走到一定的点后开始巡检。因此,可以把巡检工作转化为图论中的赋权图,用Kruskal算法[1-2]找出赋权图的最小生成树[3-6],然后进行问题的求解。
已知条件中的连通赋权图为G=(V,E,A),其中V=(v1,v2,…,v26)为顶点集,vi(i=1,2,…,26)表示26个需要巡检的点[7],v22为巡检调度中心,E为边的集合,A=(dij)26×26为邻接矩阵,其中
lij表示巡检点vi到巡检点vj的路程耗时,若巡检点vi到巡检点vj没有边相连,记为∞。
接下来用Kruskal算法找出图G的最小生成树。因为v22为巡检调度中心,所以以v22为树的根,边v22v23的权为1,为最小权边,首先选择边v22v23,接下来的每一步都从未选的边中选取边e,使它与已选边不构成圈,且e是未选边中的最小权边,直到选够21条边为止(树的边数=顶点数-1),就得到了图G的最小生成树T。
2.1 问题1的分析
如果采用固定上班时间,不考虑巡检人员的休息时间,采用3班倒,可以假设上班时间分别为0∶00-8∶00、8∶00-16∶00、16∶00-24∶00。已知大部分点的巡检周期为35 min,对于位号为XJ—0005,XJ—0010,XJ—0017,XJ—0025的点不作考虑,因为这4个点的巡检周期均在120 min以上,经过3个周期,空出来的时间就可以进行检测。
先对最小生成树进行大致分块,给出每班约需要多少人,粗略划分后,求出每一块的边权和顶点权之和,建立目标规划模型,使用Floyd算法[8-15]求出每一名工人的最短路径[16-18],再使用MATLAB[19]及LINGO,验证每班需要人数,给出合理优化的巡检线路[20]和巡检时间表。
2.2 问题2的分析
如果工人需要休息时间和进餐时间,通过问题1可知,要保证工作正常进行,必须至少同时4人在工作,若在问题1的基础上每班增加1人,由于12点左右吃饭时只能每人轮流进餐,因此吃饭时间至少持续2.5 h,不尽合理。所以在问题1的基础上每班增加2人(考虑到3班需要倒班,所以忽略夜班0∶00-8∶00需要工人数更少的情况),然后建立目标规划模型,使用MATLAB及LINGO,验证每班需要6人是否合理,并给出优化的巡检线路和巡检时间表。
2.3 问题3的分析
由问题1可知,要满足背景资料的条件,必须至少4名工人同时工作,若要把问题1中的固定上班改为错时上班,反而会增加人力成本,不可取。
问题2中,牵涉到休息和吃饭的问题,如果能合理安排,让工人错开时间上班,就可以节省人力。比如:第一组工人上班时间为3∶00-11∶30,工作时间为8.5 h,第二组工人上班时间为11∶30-19∶00,工作时间为7.5 h,第三组工人上班时间为19∶00-3∶00,工作时间为8 h。这种上班时间安排可将2次进餐时间错开,所有工人可以省去吃饭的30 min,这样工作量减少,每班5个人就可以完成,此种方法比固定上班共节省3人。因为在一定的周期内3组工人要进行调班,所以整体来看,工人的工作量仍然能保持均衡。接下来建立目标规划模型,使用MATLAB及LINGO,验证每班需要5人是否合理,并给出优化的巡检线路和巡检时间表。
可以如下安排,第一组工人上班时间为4∶00-12∶00,第二组工人上班时间为12∶00-20∶00,第三组工人上班时间为20∶00-4∶00;则每组工作时间都为8 h,第一次进餐时间无需计算,只需在6∶00时进餐1次即可,则第一班人数为5人,第二班人数为6人,第三班人数为5人,则此种方法比固定上班共节省2人。这种方式在此不进行深入讨论。本文只探讨每班5名工人工作的情形。
3 模型的建立与求解
3.1 问题1的模型建立与求解
在树T中,所有边的权之和为47,26个顶点的权之和为67,巡检点的巡检周期大部分都是35 min,那么每班的工人数要大于或等于(47+67)÷35≈3.26,由于要取整,那么每班的工人数至少要为4人,而巡检点的个数为26,考虑到每名工人在一定时间段内的工作量尽量平衡,每位工人所负责的巡检点的个数应该在26÷4=6.5≈7左右,然后将最小生成树T划分为4个部分,在划分的时候尽量满足以下几个条件:
1)划分的4块尽量接近调度中心,即接近顶点;
2)划分的各子图尽量为连通图,各子图所含顶点数在7个左右;
3)因为要进行循环巡检,所以划分的子图应容易形成圈。
按照以上的条件,对最小生成树T进行粗略分块(表1)。

表1 最小生成树的分块
每一个工人在35 min内巡检自己所负责的点,对于巡检周期较长的可以循环几次之后对该点进行巡检一次。每位工人负责的巡检区域子图分别记为G1、G2、G3、G4,记

(1)
其中qi为巡检点vi巡检所需耗时。
为使工人的工作量尽量平衡,引入1个量η进行衡量,称之为工作量均衡度,记

(2)
显然,η值越接近于0,说明工作量越均衡。
这样就建立了以下的目标函数
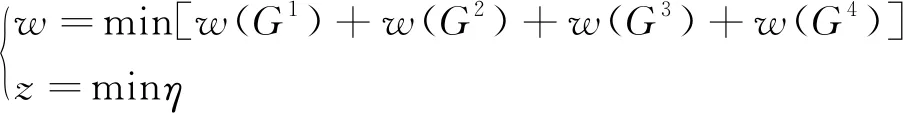
(3)
根据划分时需要满足的条件可以给出上述目标函数的约束条件。
1)因为工人都是从调度中心开始工作的,因此顶点v22应在每一个子图中,即v22∈Gk,k=1,2,3,4。
2)4个分块应包含图G的所有顶点,即
V(G1)∪V(G2)∪V(G3)∪V(G4)=V(G)
3)因为大部分点的巡检周期都是35 min,所以在35 min以内,每个工人都应在其负责的区域巡检一遍,并能够回到巡检起点,即
由上所述,可以得到问题1的目标规划模型
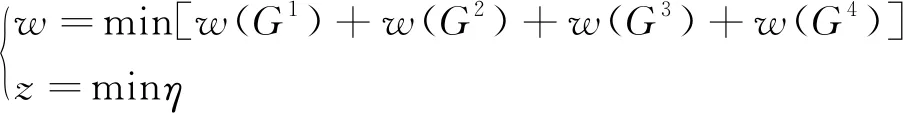
(4)

(5)
运用Floyd算法,使用MATLAB对每组求最短路径,使用LINGO求出最优回路,并对结论进行微调。
最优巡检线路及周期耗时见表2。

表2 问题1的巡检路线
表3为第一班工人从0∶00时开始时,前3个周期内26个巡检点的巡检时间。

表3 问题1的巡检时间
以后周期的巡检时间可以依次类推。
3.2 问题2的模型建立与求解
通过前面的问题分析,把6名工人负责的巡检区域子图分别为G1、G2、G3、G4、G5、G6,记
(6)
其中qi为巡检点vi巡检所需耗时。
工作量均衡度

(7)
这样就建立了以下的目标函数

(8)
根据划分时需要满足的条件可以给出上述目标函数的约束条件。
1)因为工人都是从调度中心开始工作的,因此顶点v22应在每一个子图中,即v22∈Gk,k=1,2,3,4,5,6。
2)6个分块应包含图G的所有顶点,即
V(G1)∪V(G2)∪V(G3)∪V(G4)∪V(G5)∪V(G6)=V(G)
3)35 min以内,每名工人都应在其负责的区域巡检一遍,并能够回到巡检起点,即
由上所述,可以得到问题1的目标规划模型

(9)
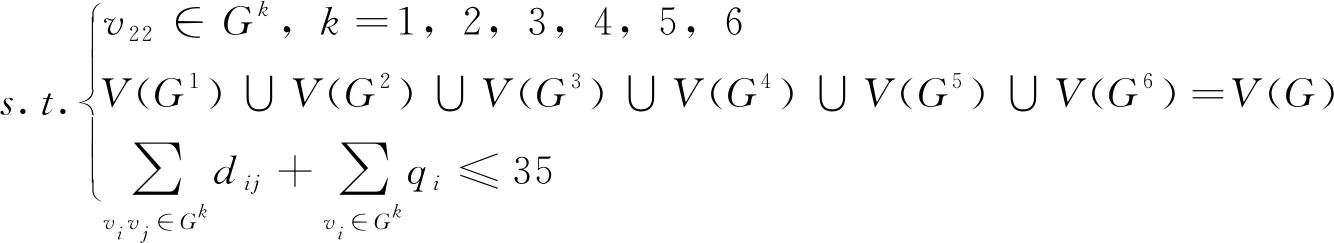
(10)
运用Floyd算法,使用MATLAB对每组求最短路径,最短路径可以确定工人在其工作区域如何以最快速度到达需要巡检的点。使用LINGO求出最优回路,因为每位工人需要在其工作区域循环巡检,因此求出的最优回路就是工人的最优巡检路线。
表4给出了每班6名工人的巡检路线,以及前3个周期的巡检耗时。

表4 问题2的巡检耗时
以甲为例,前3周期巡检耗时均为27 min,每个周期都能有空余休息时间,这样一定能保证2 h可以有5~10 min的休息时间。而吃饭的时候需要有4人在线工作,所以可以安排2人1组去吃饭,剩余4人按照问题1的巡检路线进行巡检,这样所有工人的进餐时间前后只要持续1.5 h就可以,而如果每班5人,则吃饭持续时间2.5 h时间过长,不符合要求的12时或者6时左右进餐。
表5给出了第一班工人从0∶00时开始,前3个周期内26个巡检点的巡检时间。

表5 问题2的巡检时间

表5(续)
以后周期的巡检时间可以依次类推。
3.3 问题3的模型建立与求解
通过问题3的分析,把5名工人负责的巡检区域子图分别G1、G2、G3、G4、G5,记
(11)
其中qi为巡检点vi巡检所需耗时。
工作量均衡度
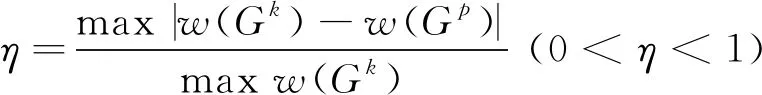
(12)
建立以下目标函数

(13)
根据划分时需要满足的条件可以给出上述目标函数的约束条件。
1)因为工人都是从调度中心开始工作的,因此顶点v22应在每一个子图中,即v22∈Gk,k=1,2,3,4,5。
2)5个分块应包含图G的所有顶点,即V(G1)∪V(G2)∪V(G3)∪V(G4)∪V(G5)=V(G)
3)因为大部分点的巡检周期都是35 min,所以在35 min以内,每个工人都应在其负责的区域巡检一遍,并能够回到巡检起点,即
由上所述,得到问题3的目标规划模型

(14)
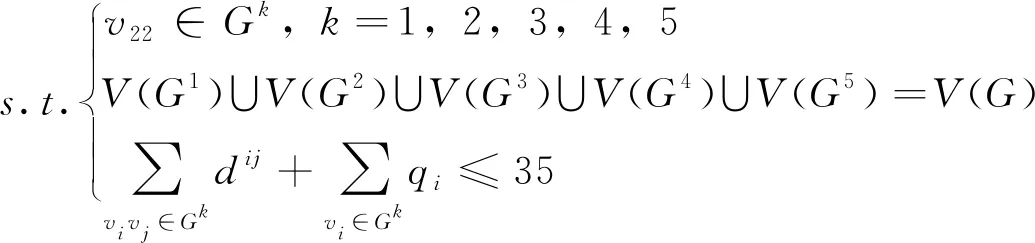
(15)
运用Floyd算法,使用MATLAB对每一子图求出最短路径,以此确定工人到达巡检点所需最短时间。然后使用LINGO求出最优回路,以此得到工人的最优巡检路线。通过对结论进行优化,最终5名工人的巡检路线见表6。

表6 问题3的巡检路线
5名工人3个周期的巡检时间见表7。

表7 问题3的巡检时间
所以若要把问题1中的固定上班改为错时上班,反而会增加人力成本,不可取。
若把问题2中的固定上班改为错时上班,考虑到长远,要进行3班调班,所以得出3班均为5人上班,比固定上班共节省3名工人。
