基于双模开环谐振器的双频带滤波器设计*
2020-06-08邢孟江李小珍代传相
易 康,邢孟江,侯 明,李小珍,代传相
(1.昆明理工大学 信息工程与自动化学院,云南 昆明 650500;2.昆明学院 信息技术学院,云南 昆明 650500)
0 引 言
随着无线通信系统的快速发展,通信协议不断更新换代,通信系统需要能兼容多个通信频段。为满足通信系统集成化、小型化、高性能、多频段的要求,双频甚至多频滤波器逐渐成为当下研究的热点之一。目前,双频滤波器的实现方法主要有以下几种:使用两个独立的带通滤波器并联实现[1-2],此方法需要增加额外的匹配网络,整个滤波器结构将偏大;使用频率变换或耦合矩阵优化[3-4],该方法设计过程较为复杂;使用多模谐振器构建双频滤波器[5-9],由于在一个谐振器中具有多个谐振模式,此方法具有结构紧凑的优点。
对正方形开环双模谐振器进行分析,采用耦合线进行馈电,提出一种双模双频带通滤波器。仿真结果表明,该滤波器中心频率分别为4.5 GHz 和6.5 GHz,3 dB 相对带宽分别为11%、5%,在阻带具有良好的抑制特性,在两通带之间具有良好的隔离度。
1 双模开环谐振器分析
开环双模谐振器的结构如图1 所示,由两个中心点重合的正方形开环谐振器组成,其中L1、L2和S1、S2分别是两个正方形开环谐振器的边长和开口尺寸,L3=0.5*(L1-L2)是连接两个正方形开环谐振器的微带线长度,Y1、Y2、Y3为所对应微带线的特征导纳。由于该双模谐振器关于T-T’平面对称,故可采用奇偶模法对其进行分析[10]。
在奇模激励时,对称面为理想电壁,可等效为虚拟短路。图2(a)为谐振器的奇模等效电路,θ1为(3L1-S1)/2 的电长度,可用θ1=β(3L1-S1)/2 计算。
此时,奇模输入导纳为:


图1 开环双模谐振器结构
在偶模激励时,对称面为理想磁壁,可等效为虚拟开路。图2(b)为谐振器的偶模等效电路,θ2为(3L2-S2)/2 的电长度,可由θ2=β(3L2-S2)/2 计算。θ3为L3的电长度,可由θ3=βL3计算偶模输入导 纳为:
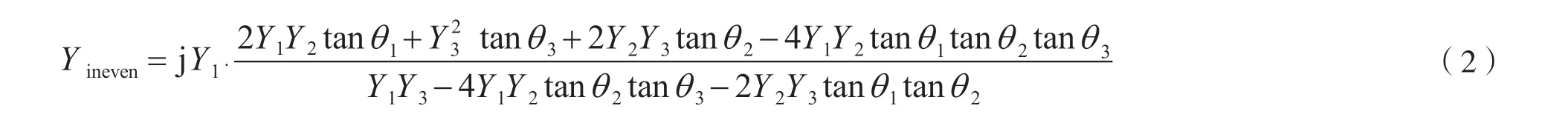
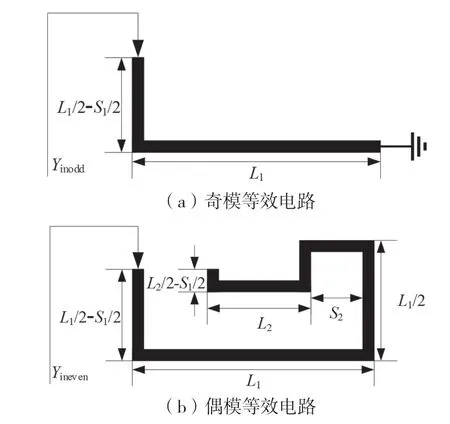
图2 谐振器结构奇偶模等效电路
为了简化设计,取Y1=Y2=Y3/2,此时偶模输入导纳为:

由传输线理论[10]可知,当输入阻抗Yin=0 时,谐振器发生谐振。于是,令Yinodd=0、Yineven=0,分别求出奇模谐振频率fodd和偶模谐振频率feven:式中εeff为有效介电常数,n=1,2,3,…。
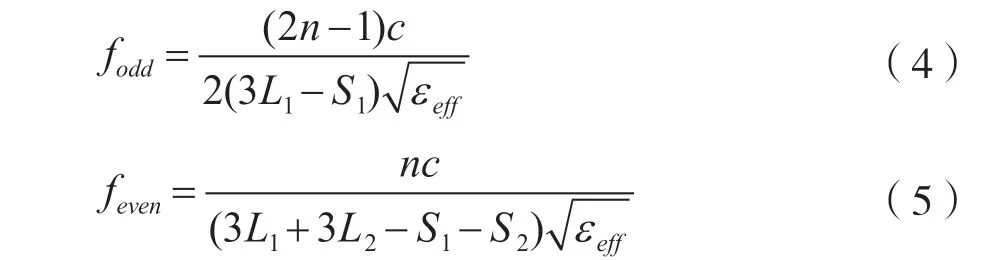
由于在设计中只用到奇模和偶模的基频谐振频率,即n=1,代入式(4)和式(5),可得:
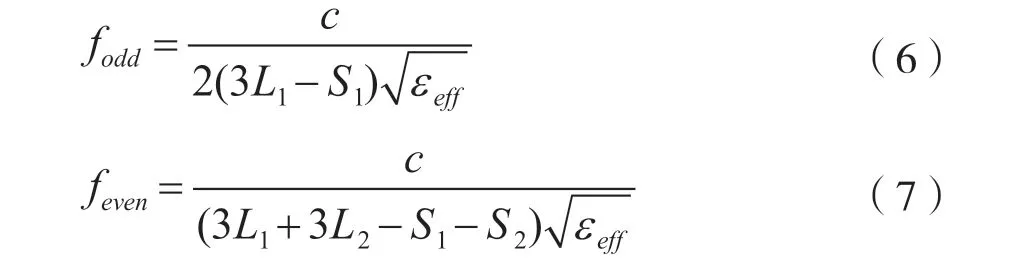
通过分析式(6)和式(7),可得出以下结论:
(1)L1发生变化,fodd、feven都会随之变化;L2发生变化时,影响的仅有feven。
(2)当谐振器发生谐振时,较小的谐振频率为奇模谐振频率fodd,较大的谐振频率为偶模谐振频率feven。
图3 为L1不变、仅改变L2大小时,该双模谐振器在弱耦合下的频率响应特性。由图3 可知,当L2减小时,奇模谐振频率fodd基本保持不变,只有偶模的谐振频率feven和两个传输零点明显右移。因此,该谐振器发生谐振时出现的两个传输零点仅与与偶模谐振频率feven相关。
由上述分析可知,当L1、L2变化时,奇、偶模谐振的频率以及传输零点也会随之变化。利用这一特性,能设计出具有良好带外抑制的滤波器。
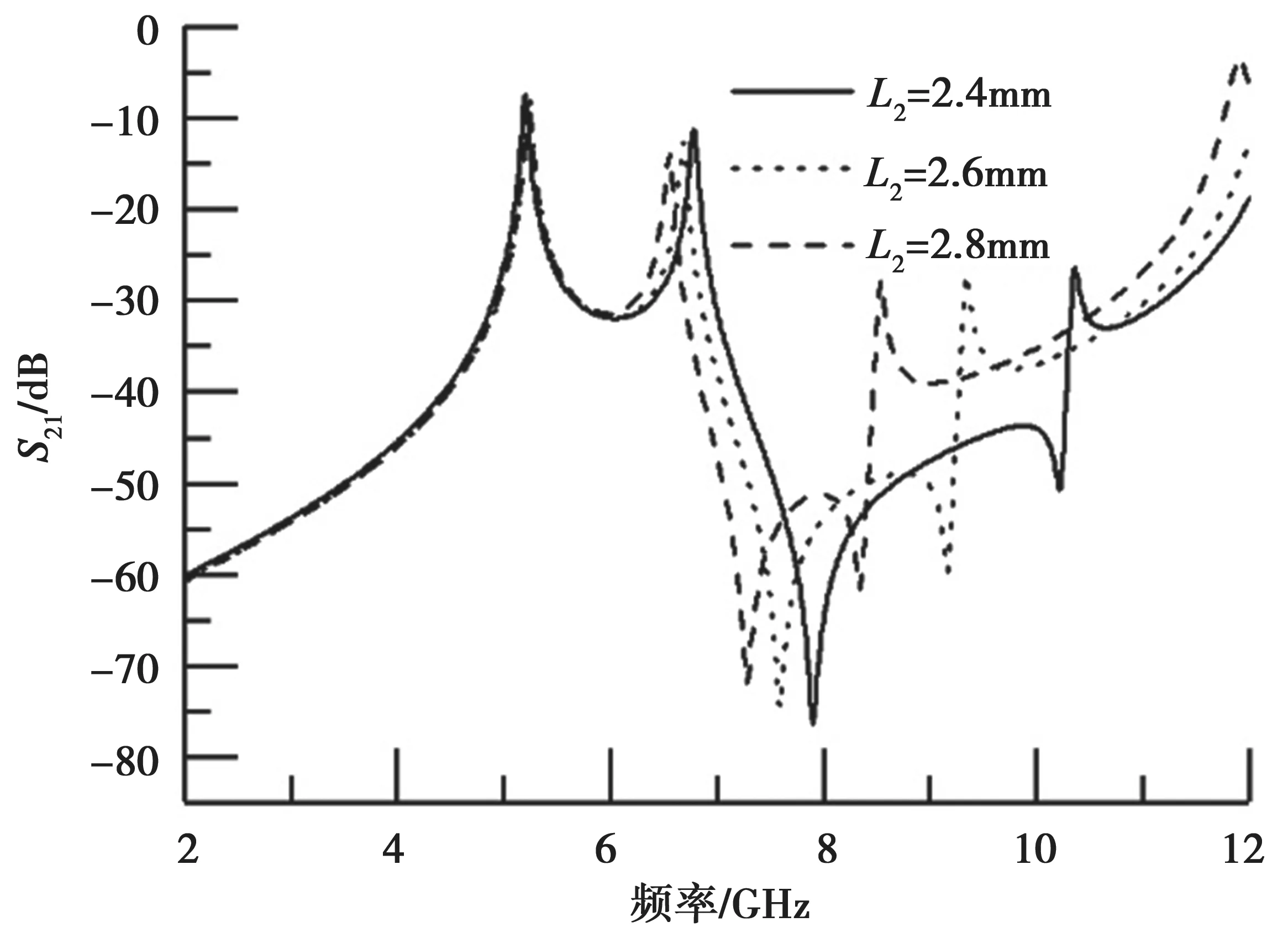
图3 L2 对双模开环谐振器的频率特性的影响
2 双频带带通滤波器设计
基于上述双模开口环谐振器分析,使用耦合系数/外部品质因数法设计一款工作在4.5 GHz/6.5 GHz 的双频带通滤波器,相对带宽FBW 分别为10%和5%。选取带内波纹值为0.01 的切比雪夫低通归一化原型值,g0=1.0,g1=1.378 2,g2=1.269 3,两个通带的外部品质因数Qen、耦合系数Kn可由式(8)、式(9)求得[10]:

求得两个通带外部品质Qen与耦合系数Kn的理论值分别为Qe1=13.782、K1=0.075 6(第一通带),Qe2=27.564、K2=0.037 8(第二通带)。
使用全波仿真软件HFSS 进行建模与仿真,该滤波器物理结构如图4(a)所示,采用两个相同的正方形双模谐振器耦合,并用耦合线对双模谐振器进行馈电。耦合拓扑结构如图4(b)所示,通带1由谐振器1 的奇模谐振频率f01和谐振器2 的奇模谐振频率f02构成,通带2 由谐振器1 的偶模谐振频率fe1和谐振器2 的偶模谐振频率fe2构成。通过HFSS 仿真后,实际的外部品质因数和耦合系数可以通过式(10)和式(11)计算[10]:

式中fh是通带中较高处的谐振频率,fl是通带中较低处的谐振频率,f0是中心频率,Δf3dB是3 dB通带带宽。
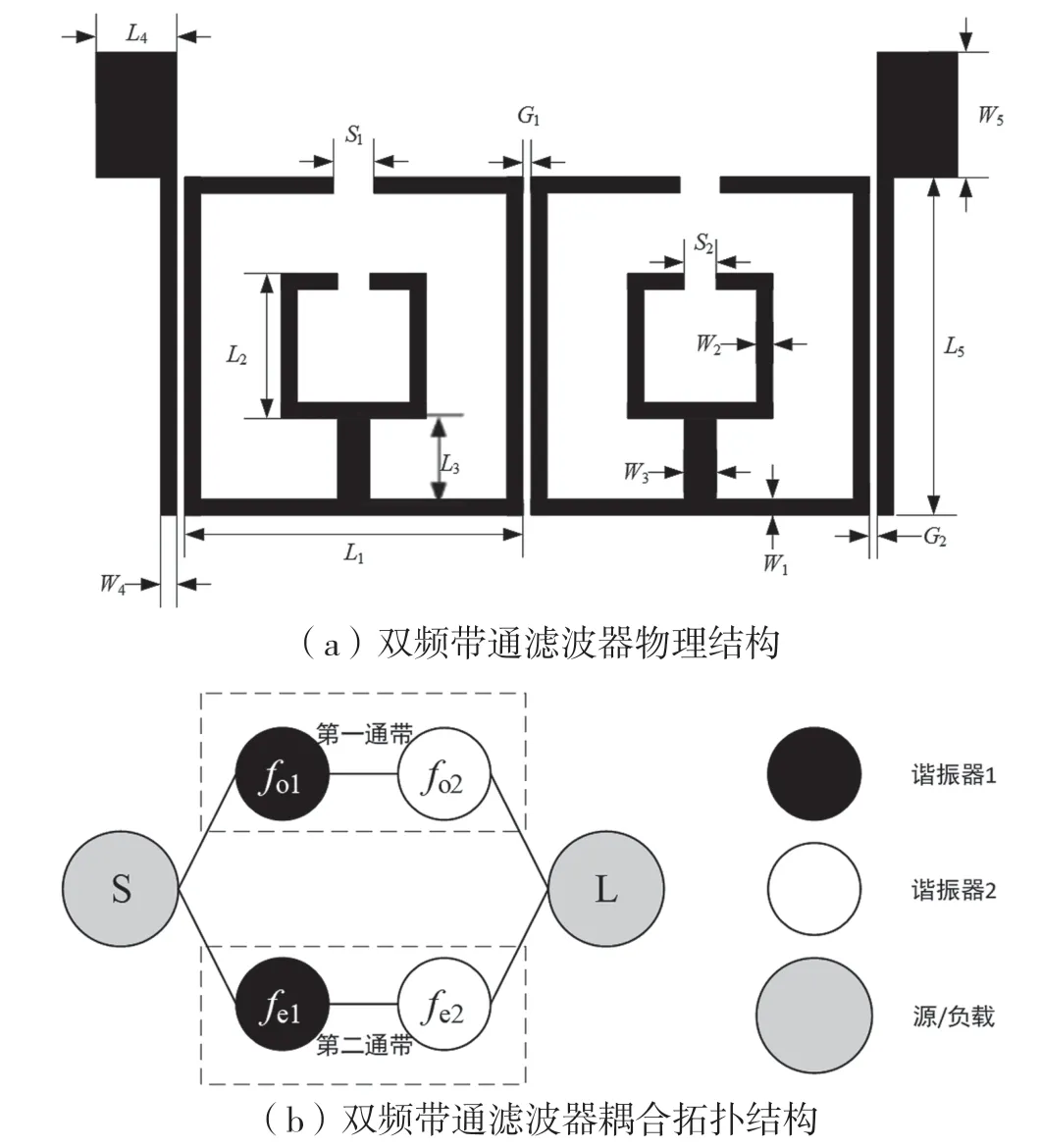
图4 双频带通滤波器物理结构和耦合拓扑结构
通过调整谐振器奇偶模谐振频率、两个谐振器之间距离以及馈电耦合线的与谐振器之间的间距,使得每个通带实际提取的qen与kn和理论求得Qen与Kn值相近,即可确定该滤波器的物理尺寸。采用相对介电常数为5.9 的ltcc(低温共烧陶瓷)作为衬底,厚度为1.08 mm,表面敷金厚度为10 μm。最终确定该滤波器中各参数数值为:L1=4.2 mm,L2=2.2 mm,L3=0.8 mm,L4=1.12 mm,L5=4.44 mm,W1=1 mm,W2=1mm,W3=2 mm,W4=1 mm,W5=1.56 mm,S1=0.5 mm,S2=0.4 mm,G1=0.12 mm,G2=0.12 mm, 整体尺寸为6 mm×11 mm×1.09 mm。
图5 为该滤波器的S参数仿真结果,两个通带的中心频率分别为4.5 GHz、6.5 GHz,对应的3 dB相对带宽分别为11%、5%。两通带带内回波损耗分别优于19.5 dB、16.5 dB,通带内的插入损耗分别小于0.6 dB、1.4 dB。该滤波器具有两个传输零点,在5.8 GHz 处的传输零点阻带抑制达到53 dB,提高了两个通带之间隔离度,在8 GHz 处的传输零点阻带抑制达到50 dB。
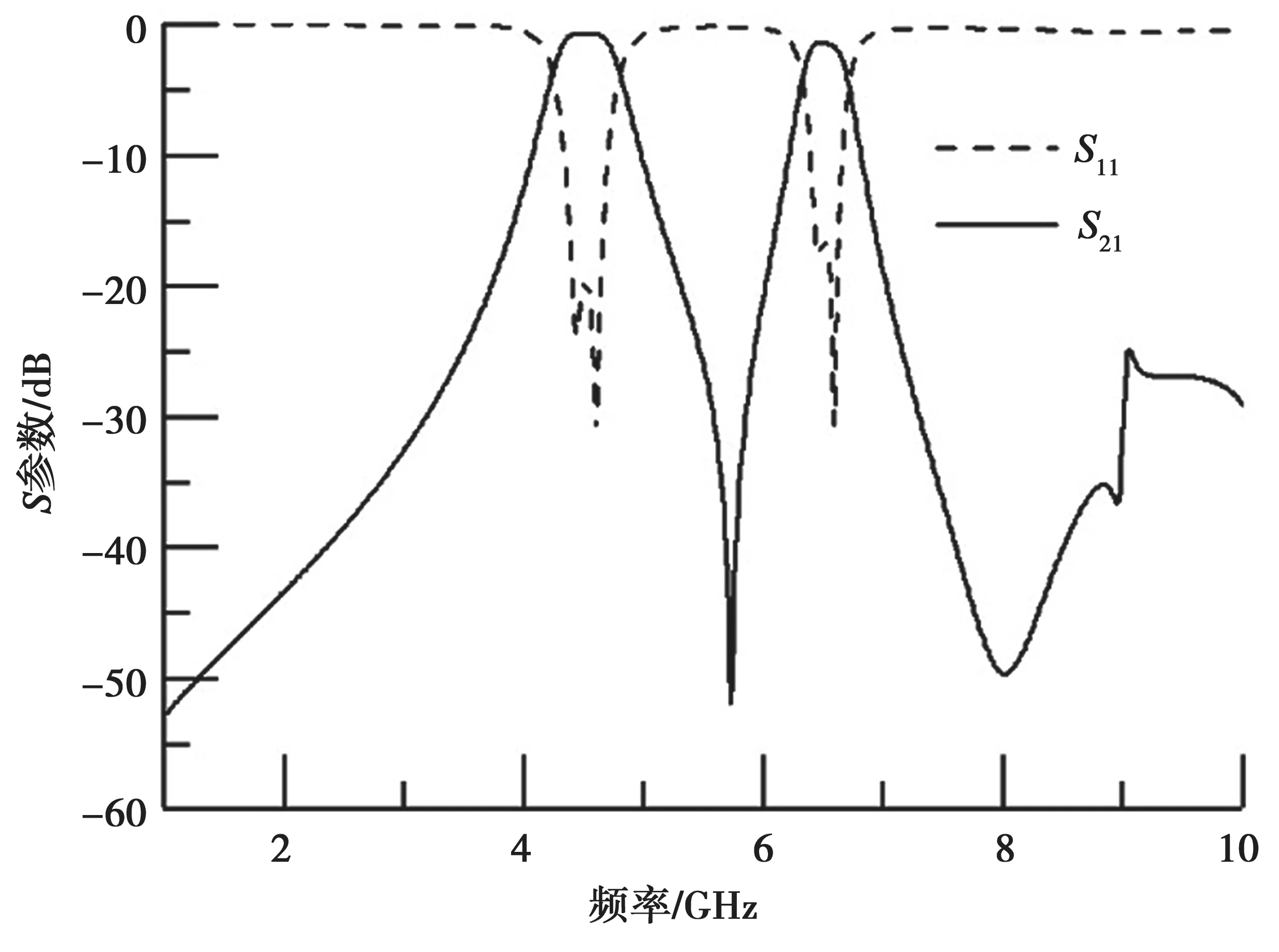
图5 滤波器的S 参数仿真结果
3 结 语
通过耦合线对两个开环双模谐振该滤波器进行馈电,实现了具有两个传输零点的双通带滤波器,两个零点分别位于两个通带之间和高频通带的右侧,极大地提高了滤波器的频率选择特性。但是,该滤波器的高频通带带内插损较大,还有待提升。该滤波器结构紧凑,带外抑制特性好,通带之间隔离度好,在无线通信系统中具有一定的实用价值。
