城轨列车车载超级电容寿命预测研究
2020-06-08石岩高锋阳张国恒高云波李浩武
石岩,高锋阳, ,张国恒,高云波,李浩武
城轨列车车载超级电容寿命预测研究
石岩1,高锋阳1, 2,张国恒1,高云波1,李浩武2
(1. 兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070;2. 甘肃交达工程检测有限公司,甘肃 兰州 730070)
城轨列车运行过程中,会对储能系统进行充放电,储能系统的超级电容组承受着周期性循环的结温波动,结温频繁变化会损伤超级电容,是列车储能系统中最易发生故障的器件之一。为了在线计算超级电容的结温状况,首先建立等效热网络模型;然后将热模型获得的结温曲线通过实时雨流计数法提取结温特征,结合所提寿命预测模型实现超级电容组的寿命预测。另外,以三维图的形式展示各平均温度和温度波动条件下超级电容组的循环寿命,为预测更多工况条件下超级电容组的寿命提供参考,以便进一步提高储能系统的可靠性和安全性。
寿命预测;雨流计数法;超级电容;结温波动
超级电容的充放电效率高,循环寿命长,且其功率密度高,因此作为储能元件在城轨列车、电动汽车等方面有重要的应用[1−2];超级电容的单体工作电压一般都很低,故在实际应用中大多采取模块化组合的方式[3],但这种模块化的结构在工作时往往会出现局部温度过高等问题[4],会加速超级电容的老化。传统的加速老化实验是由少数超级电容组在低功率条件下进行测试[5],同时考虑了不同电压和温度对超级电容老化的影响,但这种研究方法忽略了充放电循环对寿命的影响。在车辆运行过程中,超级电容组处在高功率充放电循环的工作环境中,这种高功率循环的充放电电流非常大,会引起超级电容组的温度升高,严重损伤超级电容的寿命[6]。常用的寿命预测模型有2类,如文献[7]中所描述的解析寿命模型,是基于有限的老化试验数据,利用支持向量机的方法对老化趋势进行预测,但这种模型不能反映器件的物理机理。许雪成等[8−9]基于不同温度条件下建立超级电容的物理寿命预测模型,运用阿仑尼乌斯方程对实验数据进行拟合,建立了温度与循环使用寿命关系的预测模型,其主要考虑材料的故障机制,重在分析超级电容内部的各种电极材料以及高温以阿伦尼乌斯方程的形式加速电化学反应,但其只考虑了温度的变化对寿命的影响,导致这种模型预测精度不高。本文所采用的超级电容物理寿命模型基于超级电容的应力−应变形变,结合超级电容的老化数据进行超级电容的寿命预测,可以反映超级电容寿命的物理机理,且考虑了超级电容的温度波动和平均温度对超级电容的寿命影响,可以有效提高预测精度。为实现基于结温的功率器件在线寿命预测,常使用循环计数的方法[10]。常见的循环计数法有峰值计数、ayes方法、赛道方法和简单范围计数,但在所有这些算法中,雨流算法由于其实现简单和提取数据过程中产生较少的误差而获得了广泛的应用[11−12]。传统雨流算法是基于时域历史数据的局部最大值和最小值,其不能应用于实时数据,并且难以及时准确地监测器件的健康状态,因此实际中需要采用在线雨流算法来估算器件的实时寿命[13−15]。本文首先搭建城轨列车中超级电容的充放电控制系统和等效热网络模型,用来在线计算超级电容的结温。然后运用雨流计数法提取结温曲线的平均温度和温度波动,代入到建立的寿命预测模型中,获得在给定工况下的超级电容在线寿命预测结果,并通过对比分析不同的平均温度和温度波动条件对超级电容的寿命产生的影响。
1 温度对超级电容寿命的影响
在正常情况下超级电容的循环寿命很长,要测量其循环寿命需要花费好几年的时间,不利于分析影响超级电容寿命的因素,因此老化加速试验和循环寿命预测对超级电容的实际使用具有重要的指导意义。在离线的情况下,对型号BCAP0010T01,标称电容值 10 F,单体额定工作电压 2.7 V的超级电容考虑温度影响的情况下进行加速循环试验,当超级电容容值下降到原来的20%或者等效串联电阻增大到原来的2倍就算失效。
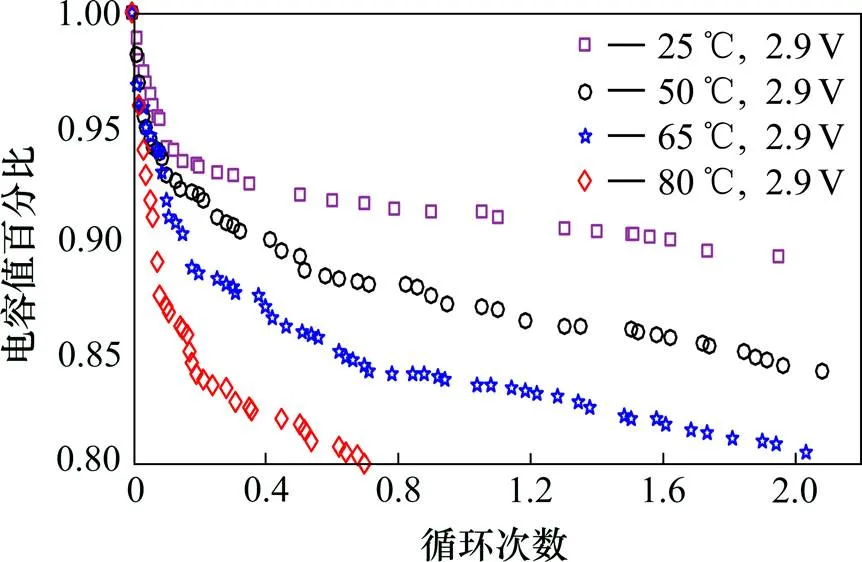
图1 温度对超级电容寿命的影响
图1为4个单体超级电容在不同温度下的循环次数和超级电容剩余寿命的实验结果,通过实验结果可以看出,当超级电容工作在25 ℃的温度下时,超级电容的循环寿命远大于2万次,但随着温度的逐渐升高,超级电容的寿命开始锐减,当温度达到80 ℃时,超级电容的循环寿命大约为7 000次,过高的温度对超级电容的损伤极大,在实际应用中,理应避免超级电容工作在过高温度的环境下。通过实验结果可以看出温度对超级电容的寿命会产生很大的影响,故在城轨列车的运行中,考虑温度的影响在线预测超级电容的寿命尤为重要。
2 等效热网络模型
在高功率场合常采用热网络模型来预测温度,并将温度与电路模型耦合以分析温度对器件性能的影响[16],其中Foster热网络模型常用于IGBT和锂电池的结温计算,不过该模型中热阻,热容值与实际物理结构无必然联系,仅能实现相关模型的“黑盒”热测试。本文采用Cauer模型,其热阻和热容参数与器件各层物理结构存在一一对应的关系,可以更好地输出结温曲线,模型结构如图 2 所示。
热路与电路中的各个物理量之间有着一一对应的关系[17],如表1所示。因此,可以利用电路数值仿真工具进行求解超级电容的结温状况,所得到的电路节点电压便是热路中的节点温度。

表1 热路与电路对偶关系

图2 Cauer热网络模型
由于Cauer 模型与超级电容的物理结构、属性有关,因此由热电比拟原理可知其的表达式为[16]
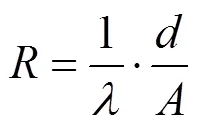
式中:为导热系数;为材料厚度;为材料传热有效面积。可表示为:
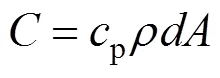
式中:p为比定压热容;为材料密度,基于所用双层超级电容的结构和物性参数,由式(1)和式(2)计算得到,1=0.5 F,1=20 Ω,2=1 000 F,2=30 Ω。等效热网络模型的结温计算表示为:

式中:j为超级电容的结温;c为超级电容的初始温度;为超级电容的发热功率;为热阻。
3 雨流计数法
3.1 雨流计数法的原理
雨流计数法主要用于工程界, 特别在疲劳寿命计算中应用非常广泛[18−19],雨流计数原理如图3所示,每个闭合磁滞回线被认为是具有指定应变的负载循环范围及其相应的平均值。例如,在对某材料施加特定应力之后,它开始张紧(从点①),导致材料变形。这种张力继续指向②,其中新的应力使材料压缩到点③。然后它开始张紧,因此经过点②,导致形成应力−应变滞后环(③−②),该变形继续到④点,之后压缩应力使材料应变减小到⑤点,然后施加正应力并且出现正应变(⑥),之后,通过压缩材料,发生材料变形,并且经过点⑤形成另一个应力−应变滞后环,该过程将持续到所有数据都分析完毕。雨流法得到的应变数据正是根据材料的这种应力−应变的特性得到的。
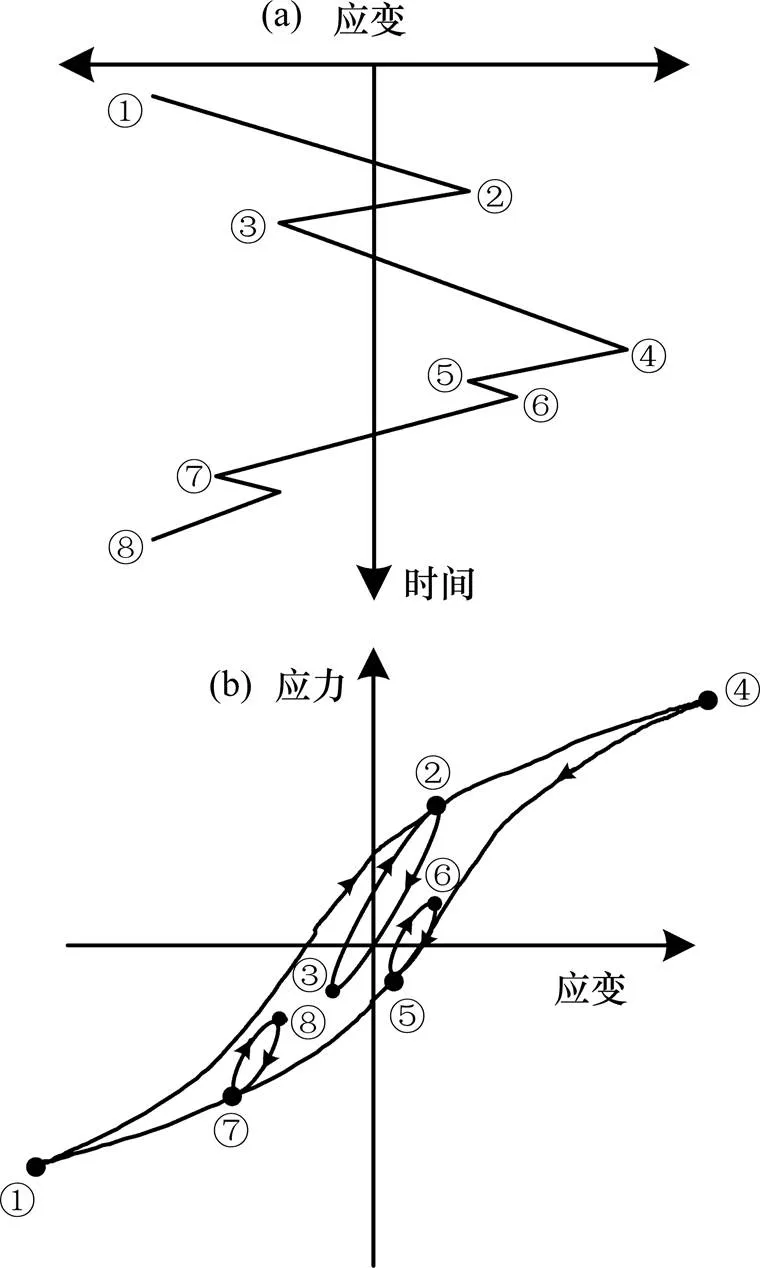
(a) 载荷序列;(b) 应力−应变曲线
3.2 在线雨流算法的运用
离线雨流计数方法常用于生成温度范围直方图以识别定期加载周期,应用传统的雨流计数算法进行实时温度的数据提取是非常具有挑战性的,因为在实际列车运行中算法必须应用于一系列温度和时间的数据,这些数据中包含许多最大值和最小值,首先必须先存储和处理温度值的数据,定期获取等效的温度曲线,然后通过频率直方图来描述涵盖温度摆动的有限范围和可能的平均温度,这给温度的实时处理带来了很大的困难。为了解决上述问题,采用新的实时雨流算法,确保实时控制流程不会中断。启动算法后,实时雨流计数算法会首先处理大小可变的缓冲区中的数据,分辨出最小值和最大值,然后将存储区中的数据,使用递归方法在线识别出全周期和半周期的运行结果,实时雨流算法的流程图如图4所示。

图4 实时雨流算法
图4中:是温度值;Δ表示温度的波动范围;平均温度则用m表示,其中,m=m+/2。在未达到设定的运行时间之前,一旦最小值堆栈中存在最小值,它就会与输入的新值进行比较,如果新值小于旧值,那么将检查最大值堆栈的保存值。用指针trmax表示最大值堆栈中存在的最大值个数,如果只有一个最大值存在,则会检查出一个半周期,温度波动Δ将在这个最大值和旧的最小值之间作差,同时计算出平均值,然后从最小值中移除旧的最小值,并用新的最小值来替换。如果最大值指针trmax指示了多个最大值,则表明确定了一个完整的全周期,温度波动Δ将是新的最大值和旧的最小值之间的差值,同时旧的最小值和新的最大值都将被移除。当出现新值大于最小值堆栈的情况下,新值将保存在最小值堆栈的左侧,作为最小值堆栈中的第1个值。如果最小值堆栈中包含的数值超过一个值,则将以递归方式重复进行运算,堆栈大小根据保存的数据大小动态变化。
4 寿命预测模型的建立
阿伦尼乌斯方程,可以确定热氧化老化所需的应力,也可以计算产品在内外部压力下产生的变化,在研究长寿命周期产品的寿命时,研究人员通常采用加速寿命试验来验证产品的生命周期,温度常常作为加速应力来研究这类化学反应,基于此提出了阿伦尼乌斯寿命预测模型[20],此模型可用来预测产品的最高使用温度,在温度升高到一定的值时,会出现寿命急剧下降的情况,预测模型如下式所示:

式中:f为失效前的循环次数;A为常数;为活化能;k为玻尔兹曼常数;为热力学温度。
研究指出,温度波动Δj和平均温度m是决定器件寿命、影响寿命预测模型精度的重要参量,所以,在阿伦尼乌斯模型的基础上,提出Lesit寿命预测模型,预测失效前的循环次数[21],如下式所示:
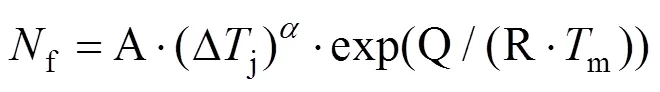
式中:R为气体常数,由于已经公开发表的文献中所开展的功率循环试验,采用超级电容的生产厂家,型号均不相同,所得到的A和Q也均不相同。本文采用第1节所述的超级电容型号,运用matlab工具箱,以所提模型为基础,对加速寿命实验数据进行拟合,如图5,其中拟合系数2为0.976,拟合具有较高精度,得到的寿命预测模型如下式 所示:
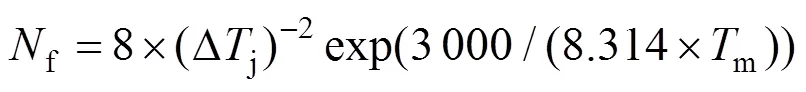

图5 超级电容寿命实验数据拟合
5 仿真验证
超级电容的寿命预测流程图如图4所示,将超级电容的功率损耗和热阻抗结合输入到热网络模型中,然后用雨流计数算法得到结温曲线的波动值和平均值,将得到的值输入到寿命预测模型中,即可得到在列车运行期间超级电容的实时预测寿命,一个运行周期的仿真时间设置为62 s,系统参数如表2所示。

图6 在线寿命预测模型框图
图7(a)为车辆运行时超级电容的功率变化情况,在0~11 s时,列车开始启动,超级电容为列车供电,超级电容输出功率迅速增大,之后,11~26 s列车进入平稳运行阶段,之后列车开始减速运行,从28~44 s列车在低速情况下运行一段时间,之后列车进入制动阶段,直到列车停止运行,在这一过程中,能量反馈到超级电容中。

表2 系统仿真参数

(a) 超级电容的功率变化情况;(b) 超级电容SOC变化情况;(c) 超级电容的电压;(d) 超级电容结温曲线
图7(b)和图7(c)为在一个仿真周期内车辆运行时超级电容的充放电情况,可以看到在列车运行过程中,在列车进入制动阶段之前,超级电容一直处于放电状态,超级电容组的荷电状态(State of Charge,SOC)和电压一直在降低,当进入制动状态之后,由于能量反馈的原因,超级电容的SOC 和电压均升高,其中,由于超级电容和负载之间未接DC-DC变换器,导致在制动过程中,电压出现了较大的波动。
在列车运行过程中,超级电容的温度会伴随着运行工况而发生改变,如图7(d)所示。设置超级电容组的初始环境温度为20 ℃,城轨列车中超级电容模组运行时承受着周期性循环的结温波动,通过雨流算法在线提取超级电容的平均温度和温度波动,并将提取到的数值代入到所建立的寿命预测模型中,得到在如图7(a)中所示的超级电容组循环运行工况下,超级电容组的寿命为可循环20 919次,而当超级电容的初始环境温度为30 ℃时,在图7(a)中所示运行工况下,超级电容组的寿命为1 479次,这2种工况下温度波动的幅值几乎没变,平均温度却显著增加了,可见在大功率列车运行过程中,平均温度对超级电容的寿命影响很大。

表3 整车超级电容组寿命预测结果
为预测更多工况下超级电容的寿命,由寿命预测模型预测超级电容的寿命随温度波动和平均温度变化的趋势,并和实际实验数据所得到的结果进行对比。从图8中可以看出,随着平均温度的升高和温度波动的增大,超级电容的预测寿命和实际寿命的减少趋于一致。当平均温度和温度波动增大时,超级电容的寿命急剧减少,所以在实际工况中,应尽量避免超级电容长时间工作在过高的温度中,可以通过调节控制系统改变负载工况,减缓超级电容的发热情况,延长超级电容的寿命。

图8 平均温度、温度波动和循环次数的关系
6 结论
1)所提在线雨流算法可以获得等效周期温度波动值和平均值,可以实时处理热网络模型输出的温度−时间数据,在每个结温时刻可以提取全循环和半循环中的极值,而不必使用包含大量极值的历史数据,实现了在线预测城轨列车车载超级电容寿命的目的。
2)车载超级电容周期性循环的结温波动对其寿命影响很大,因此,当出现超级电容寿命急剧下降时,可通过在线监测超级电容的健康状态调整控制策略,降低超级电容的压力,以提高超级电容的使用寿命。
[1] Kouchachvili L, Yaïci W, Entchev E. Hybrid battery/ supercapacitor energy storage system for the electric vehicles[J]. Journal of Power Sources, 2018, 374: 237− 248.
[2] 夏欢, 杨中平, 李旭阳, 等. 基于动态阈值控制策略的城轨超级电容储能系统寿命优化研究[J]. 铁道学报, 2016, 38(9): 23−30. XIA Huan, YANG Zhongping, LI Xuyang, et al. Life optimization of urban rail supercapacitor energy storage system based on dynamic threshold control strategy[J]. Journal of the China Railway Society, 2016, 38(9): 23− 30.
[3] 顾帅, 韦莉, 张逸成, 等. 超级电容器老化特征与寿命测试研究展望[J]. 中国电机工程学报, 2013, 33(21): 145−153. GU Shuai, WEI Li, ZHANG Yicheng, et al. Prospects of aging characteristics and life testing of supercapacitors[J]. Proceedings of the CSEE, 2013, 33(21): 145−153.
[4] Ruch P W, Cericola D, Foelske-Schmitz A, et al. Aging of electrochemical double layer capacitors with acetonitrile-based electrolyte at elevated voltages[J]. Electrochimica Acta, 2010, 55(15): 4412−4420.
[5] Kötz R, Ruch P W, Cericola D. Aging and failure mode of electrochemical double layer capacitors during accelerated constant load tests[J]. Journal of Power Sources, 2010, 195(3): 923−928.
[6] Bohlen O, Kowal J, Sauer D U. Aging behaviour of electrochemical double layer capacitors: Part II. Lifetime simulation model for dynamic applications[J]. Journal of Power Sources, 2007, 173(1): 626−632.
[7] 张莉, 时红雷. 超级电容器的老化趋势分析[J]. 电子测量与仪器学报, 2018, 15(7):187−191 . ZHANG Li, SHI Honglei. Analysis of aging trend of supercapacitors[J]. Journal of Electronic Measurement and Instrument, 2018, 15(7):187−191 .
[8] 许雪成, 刘恒洲, 卢向军, 等. 超级电容器容量寿命预测模型研究[J]. 电源技术, 2019, 43(2): 100−102, 112. XU Xuecheng, LIU Hengzhou, LU Xiangjun, et al. Research on capacity prediction model of supercapacitor[J]. Power Technology, 2019, 43(2): 100− 102, 112.
[9] Uno M, Tanaka K. Accelerated charge–discharge cycling test and cycle life prediction model for supercapacitors in alternative battery applications[J]. IEEE Transactions on Industrial Electronics, 2012, 59(12): 4704−4712.
[10] Mainka K, Thoben M, Schilling O. Lifetime calculation for power modules, application and theory of models and counting methods[C]// European Conference on Power Electronics & Applications, 2011.
[11] Gopireddy L R, Tolbert L M, Ozpineci B, et al. Rainflow algorithm-based lifetime estimation of power semiconductors in utility applications[J]. IEEE Transactions on Industry Applications, 2015, 51(4): 3368−3375.
[12] 宾洋, 于静美, 朱英凯, 等. 实时雨流计数法及其在钴酸锂电池健康状态建模中的应用[J]. 中国电机工程学报, 2017(12): 269−277, 334. BIN Yang, YU Jingmei, ZHU Yingkai, et al. Real-time rain flow counting method and its application in health state modeling of lithium cobalt oxide battery[J]. Proceedings of the CSEE, 2017(12): 269−277, 334.
[13] Musallam M, Johnson C M, Yin C, et al. Real-time life consumption power modules prognosis using on-line rainflow algorithm in metro applications[C]// Energy Conversion Congress & Exposition, 2010.
[14] Nagode M, Hack M. An online algorithm for temperature influenced fatigue life estimation: Stress-life approach[J]. International Journal of Fatigue, 2004, 26(2): 163−171.
[15] Vahid S, Hossein I E, Yvan A. An efficient online time-temperature-dependent creep-fatigue rainflow counting algorithm[J]. International Journal of Fatigue, 2018, 116: 284−292.
[16] 刘宾礼, 罗毅飞, 肖飞, 等. 适用于器件级到系统级热仿真的IGBT传热模型[J]. 电工技术学报, 2017(13): 7−19. LIU Binli, LUO Yifei, XIAO Fei, et al. IGBT heat transfer model for device-level to system-level thermal simulation[J]. Transactions of China Electrotechnical Society, 2017(13): 7−19.
[17] 杨俊, 汤广福, 曹均正, 等. HVDC阀晶闸管结温计算等效电路模型[J]. 中国电机工程学报, 2013, 33(15): 156−163. YANG Jun, TANG Guangfu, CAO Junzheng, et al. Equivalent circuit model for calculation of thyristor junction temperature of HVDC valve[J]. Proceedings of the CSEE, 2013, 33(15): 156−163.
[18] 孙丽, 刘永臣. 雨流计数法及在车辆疲劳损伤分析中的应用综述[J]. 装备制造技术, 2012(12): 75−77. SUN Li, LIU Yongchen. Review of rainflow counting method and its application in vehicle fatigue damage analysis[J]. Equipment Manufacturing Technology, 2012(12): 75−77.
[19] YANG B, YU Jingmei, ZHU Y, et al. A Real-time rain flow algorithm and its application to state of health modeling for LiCoO_2 lithium-ion batteries[J]. Proceedings of the Csee, 2017, 37(12): 3627−3635.
[20] ZHOU J, YAO J, HU H H, et al. Accelerated aging life evaluation method of silicone rubber based on segmented nonlinear Arrhenius model[J]. Material Research Innovations, 2016, 19(Suppl 5): 855−860.
[21] Dusmez S, Heydarzadeh, Mehrdad, et al. Remaining useful lifetime estimation for power MOSFETs under thermal stress with RANSAC outlier removal[J]. IEEE Transactions on Industrial Informatics, 2017, 13(3): 1271−1279.
Life prediction of vehicle supercapacitors for urban rail trains
SHI Yan1, GAO Fengyang1, 2, ZHANG Guoheng1, GAO Yunbo1, LI Haowu2
(1. School of Automation and Electrical Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China; 2. Gansu Jiaoda Engineering Inspection Co. Ltd, Lanzhou 730070, China)
The energy storage system of the urban rail train is charged and discharged during operation. The supercapacitor banks of the energy storage system are subject to cyclical fluctuations in the junction temperature. Frequent fluctuation of junction temperature in periodic cycle can damage the supercapacitor, which makes the supercapacitor component one of the most vulnerable devices in train energy storage system. In order to calculate the junction temperature of the supercapacitor online, the equivalent thermal network model was established firstly. Then the junction temperature curve obtained by the thermal model was extracted by real-time rainflow counting method, and combines with the proposed life prediction model, realizing life prediction of supercapacitor banks. In addition, the cycle life of the supercapacitor group under different average temperature and temperature fluctuation conditions was shown in the form of a three-dimensional graph, which provides a reference for predicting the life of the supercapacitor group under more working conditions, so as to further improve the reliability and security of the energy storage system.
life prediction; rain flow counting method; super capacitor; junction temperature fluctuation

TM922.7
A
1672 − 7029(2020)05 − 1279 − 07
10.19713/j.cnki.43−1423/u.T20190815
2019−09−12
国家重点研发计划资助项目(2017YFB1201003-020);甘肃省科技计划资助项目(18CX4JA004)
高锋阳(1970−),男,甘肃兰州人,教授级高工,从事车载储能技术的研究;E−mail:1484929203@qq.com
(编辑 阳丽霞)
